梯形卸荷槽对外啮合齿轮泵困油压力与流量脉动影响的研究

魏列江，李 涛，卢利锋，强 彦, 罗小梅

(1.兰州理工大学 能源与动力工程学院，甘肃 兰州 730050；2.北方车辆研究所，北京 100071)

引言

齿轮泵广泛地应用在各种液压机械上，主要优点是：结构简单紧凑，体积小，重量轻，自吸性能好，工作可靠，寿命长[1]。渐开线外啮合齿轮泵作为齿轮泵的一种，依靠相互啮合的齿轮对轮齿与壳体之间形成的封闭容腔容积变化完成吸油排油。根据齿轮啮合连续稳定传动原理，齿轮的重合度系数须大于1，即在某段时间内，同时有2对轮齿啮合，这时在这2对轮齿和两侧端板之间就形成了和吸、排油腔均不相通的闭死容积[2]，油液在困油区域内受压缩或膨胀导致困油区压力发生急剧变化，出现压力冲击、噪声、振动、气蚀等危害齿轮泵的现象。大部分研究都关注于在浮动侧板上开卸荷槽改善困油现象，卸荷槽形式上可采用矩形、圆形[3]、双重型[4]、耳形[5]、渐开线型[6]，但仍不能满足齿轮泵高转速下卸荷的需要。关于齿轮泵困油现象主要通过优化齿形参数[7-9]、优化卸荷槽形状使困油容积最小，从结构的角度出发在源头缓解困油现象。SANG-YEOL K等[10]使用一种特制的固定端板式外齿轮泵，并在其上安装了微型半导式压力传感器，以此来测量主、从动齿面所截留的空间内压力，从而精确设计了该外齿轮泵上的泄压槽位置；杨元模[11]在齿轮泵中增加一条连接困油区与进油区的卸荷槽、高压区与进油区的卸荷通道两种方法，使泵的出油压力与流量较为稳定；李玉龙[12-13]基于常用的矩形卸荷槽，针对双齿啮合区和单齿啮合区不同的啮合特点和卸荷措施，设计了一种具有更大卸荷面积、易于加工的双斜型卸荷槽，并分析了双斜型卸荷槽对双齿、单齿啮合区困油压力的降低效果，还利用龙格-库塔法的迭代运算，获得高速下困油压力和齿轮副振动在一个困油周期内的动态仿真结果，指出了高速下应尽量通过卸荷槽结构的创新设计来降低困油压力和减缓振动；牛兰芹等[14]采取在泵壳底安装储放器的结构改进措施，消除了困油现象给齿轮泵工作带来的危害；仇晓燕[15]应用基于齿形修正方法，仿真分析了齿轮泵的压力分布情况，详细研究了齿轮泵工作过程中困油容积的变化情况。对于流量脉动特性的研究，NOAH D M[16]推导了主、从动齿轮不同齿数时的外齿轮泵理论流量脉动公式，但是未考虑卸荷槽对流量脉动的影响；CAMPO S[17]和ERTURK N等[18]分析了吸油腔吸油不足现象对外齿轮泵流量特性的影响并以可视化手段对结论进行了验证；HUANG K等[19]利用可以精确有效计算外啮合齿轮泵流量的封闭式流量公式，研究了外啮合齿轮泵的流量特性，并最后讨论了齿数、模数、压力角、齿顶系数等设计参数对泵流量特性的影响；CHEN等[20]在考虑流量脉动、压力分布、泄漏、啮合条件的情况下，利用Modelica/MWorks软件对外啮合齿轮泵整个工作过程进行了建模，并对泵瞬时流量特性进行了计算；王建等[21]为了降低齿轮泵的流量脉动，提出了基于流量脉动系数的齿轮齿廓的主动设计方法，分析了基于极距和压力角函数的齿廓方程的数学描述方法，建立了基于流量脉动系数的齿轮泵中齿廓的主动设计的数学模型；张永祥等[22]提出控制面积法，讨论卸荷槽对降低齿轮泵流量脉动的影响，得出流量脉动和齿轮啮合位置关系；郜立焕等[23]对带有和不带有缓冲槽的外啮合齿轮泵的流量和流量脉动系数进行了计算和比较，讨论了设计参数齿数和齿顶高系数对外啮合齿轮泵的流量特性的影响；李玉龙[2]以无齿轮侧隙和对称双矩形卸荷槽为例，用泵排油区域封闭容积的精确计算方法，研究了困油压力对外啮合齿轮泵的流量脉动影响。

双斜型卸荷槽较矩形能提升卸荷面积、有效降低困油区最大压力峰值改善了困油现象、且结构简单易于加工[12]，但其卸荷面积提升幅度不大，困油压力峰值降低不明显。本研究基于双斜型卸荷槽、根据齿轮的啮合特点以及啮合过程中困油腔容积的变化过程，对原耳形卸荷槽进行了优化，设计了一种梯形卸荷槽，目的是降低困油区压力与出油口流量脉动，有效改善外啮合齿轮泵的困油现象与出油口流量脉动现象。

1 原耳形卸荷槽与新型卸荷槽的结构设计

1.1 原耳形卸荷槽困油过程分析

齿轮泵的困油容积变化是一个由大变小再变大的过程[24]。在困油容积变化过程中，由于困油容积最大时,卸荷槽与齿间形成的困油容积连通情况一致，故本研究略去困油容积由小再变大的过程。

图1为齿轮泵困油区域最大时的耳形卸荷槽结构，其由3段圆弧和2段直线构成。在齿轮泵工作过程中，当上1对齿即将退出啮合，下1对齿即将进入啮合时，出现了困油容积最大区域，此时，只有原耳形卸荷槽的“上耳部”连通了困油区域，起到了卸荷作用；当齿轮转至啮合点与节点对称时，齿间形成的困油容积最小[24]，此时只有耳形卸荷槽大圆弧段的左下一小部分连通了困油区域，具有微小的卸荷作用。

图1 耳形卸荷槽结构及齿轮泵的困油过程

1.2 梯形卸荷槽的设计过程

梯形卸荷槽的总体结构如图2所示，由6条线段组成，包括4段直线段和2段圆弧曲线。

(1)在三维软件中生成工况一，前一对齿仍处于啮合状态，后一对齿刚进入啮合时，主动齿轮O1、从动齿轮O2的齿廓图，如图2a所示，两齿轮基圆交点为节点a；作与两齿轮中心O1O2连线平行且距离为m/2(m为齿轮模数，下同)的直线bc，且ab的连线经过啮合点；过c点的水平线与从动齿轮的齿根过渡线共线，连接直线bc，做水平线de至出口侧边线，水平线de与产生困油区域的从动轮齿根过渡曲线距离为2 mm；直线bc与de间圆弧为φ2.0；至此，完成梯形卸荷槽的两段直线段与一段圆弧。

(2)在三维软件中生成与工况二，工况一相比，齿轮转过一个齿时的齿廓图，如图2b所示，两齿轮基圆的交点为a；延长从动齿轮的齿顶直线，与过d点且平行于直线O1O2的直线相交于点f；作水平且与主动齿轮内径相切的直线hg，在点g和点f间以φ4.0的圆弧光滑过渡。至此，完成另外2段直线段与另1段圆弧，从而完成整个梯形卸荷槽的结构设计。

如图2所示，随着齿轮转动，困油容积减小时，梯形卸荷槽与出油侧相通；困油容积增大时，梯形卸荷槽与吸油侧相通；另外需说明，耳形与梯形卸荷槽的槽深均为2.3 mm。

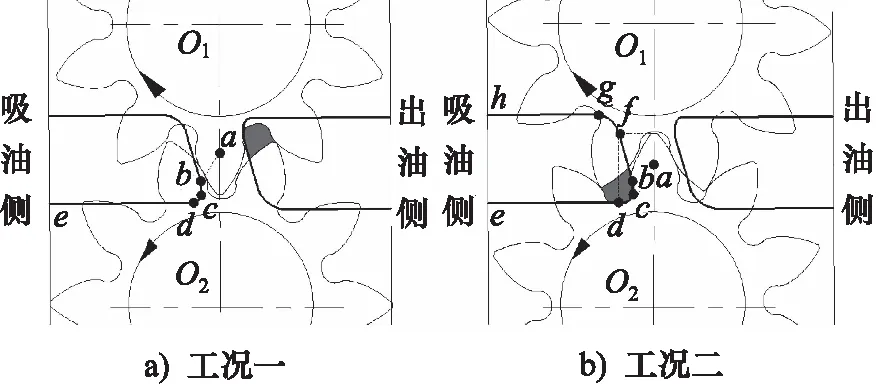
图2 梯形卸荷槽总体结构

2 仿真过程分析

2.1 齿轮泵的建模

根据耳形卸荷槽、梯形卸荷槽，在三维软件中分别建立外齿轮泵的三维模型，并抽取流体域进行仿真计算，其中渐开线齿轮及齿轮泵间隙参数如表1所示。

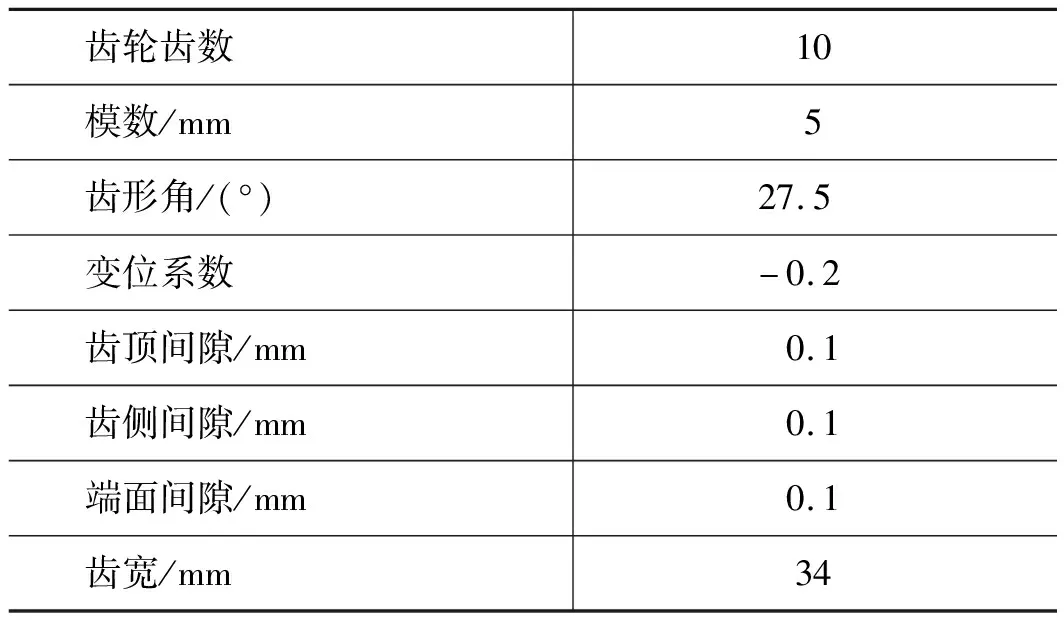
表1 渐开线齿轮及齿轮泵间隙参数

2.2 流体动力学理论分析基础

齿轮泵内部复杂的流体流动过程也要满足物理守恒定律，基本的守恒定律包括：质量守恒定律、动量守恒定律、能量守恒定律。如果流动包含有不同组分的混合或相互作用，还要满足组分守恒定律。控制方程是这些物理守恒定律的数学描述[25]。

1)连续性方程

连续性方程是质量守恒定律在流体力学中的数学描述，该定律表述为：单位时间内流体微元中质量的增加等于同一时间间隔内流入该微元体的静质量。连续性方程可写作：

(1)

式中，ρ—— 流体密度

t—— 时间

u，v，w—— 速度矢量在x,y,z坐标轴下的分量

2)动量方程(N-S方程)

动量方程基于牛顿第二定律，该定律表述为：微元体中流体动量对时间的变化率等于外界作用在微元体上的各种力之和。动量方程写作：

(2)

式中，u为液体的速度矢量；Su，Sv，Sw是动量守恒方程的广义源项，Su=Fu+sx，Sv=Fv+sy，Sw=Fw+sz，sx，sy，sz表达式如下：

(3)

3)能量方程

能量方程是热力学第一定律在流体力学中的表达，该定律表述为：微元体中能量的增加率等于进入微元体的净流量加上体积力与表面力对微元体所做的功。以温度T为变量的能量方程可写作：

(4)

式中，k为流体热传导系数；ST为流体内热源及由于黏性作用于流体的机械能转换为热能的部分，这项在一般情况下不予考虑；Cp为流体的比热容。

4)湍流模型

RNGk-ε湍流模型是在湍动能方程的基础上，引入了一个关于湍动能耗散率ε的方程，使得在计算速度梯度较大的流场时精度更高，模型中考虑了旋转效应，对于强旋流动计算精度也得到提高。对于齿间油液在旋转流动过程中，存在弯曲流动，因此，此模型对于模拟齿轮泵流场是最合适的。湍动能k和湍流耗散率ε相对应的运输方程为：

Gk+Gb-ρε-YM+Sk

(5)

(6)

式中，Gk—— 由层流速度梯度而产生的湍流动能

Gb—— 由浮力产生的湍流动能

YM—— 由于可压缩湍流中过度扩散产生的波动

C1ε，C2ε，C3ε—— 常量

σk，σε——k方程和ε方程的湍流普朗特数

Sk，Sε—— 用户自定义的源条件

μl—— 湍流速度

2.3 仿真计算模型、计算边界条件及工质物理参数

1)网格参数设置及计算域网格

建立齿轮泵模型后，抽取流体域后得到计算域模型；在数值计算软件PumpLinx中以相同的网格参数设置划分网格，网格参数设置如表2，划分网格后计算域如图3所示。

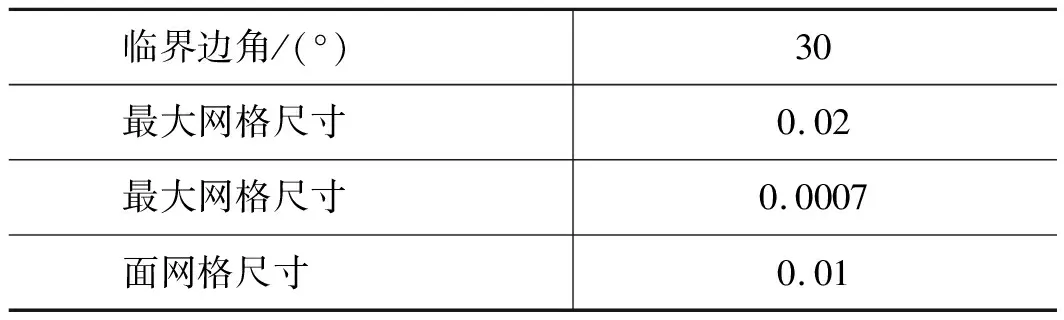
表2 网格参数设置表

图3 耳形、梯形卸荷槽流体计算域网格

2)计算边界条件及工质物理参数

为说明该梯形卸荷槽对降低困油区压力与出油口流量脉动的有效性，计算工况选4组：选定液压泵进口压力均为0.1 MPa，选取出油口压力为1.0, 1.5, 2.0, 2.5 MPa，对应的齿轮泵的转速分别为1000, 2000, 3000, 4000 r/min，计算工况如表3；工质选择46#航空液压油，物理参数如表4。

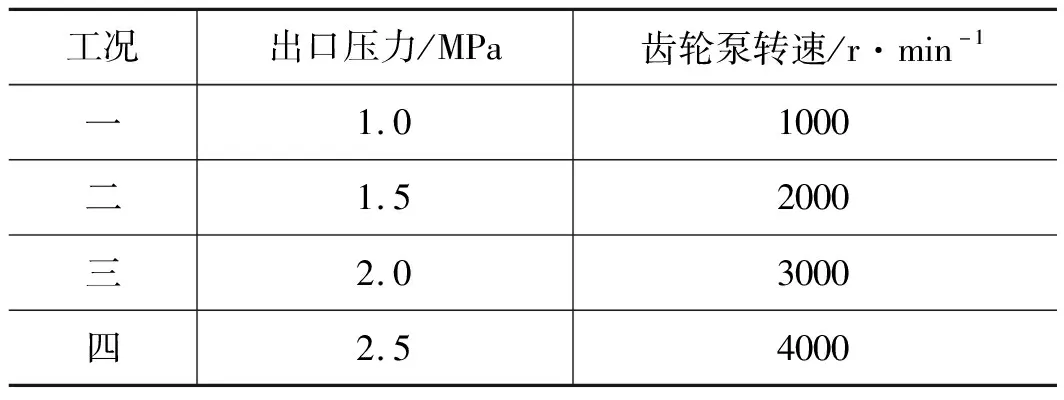
表3 计算工况

2.4 监测点的设置

在耳形和梯形卸荷槽所在的三维模型中，在相同的困油容积处分别设置压力监测点1、2，以耳形卸荷槽为例，监测点布置位置如图4所示。

图4 压力监测点位置

3 计算结果对比分析

通常齿轮泵2个齿的齿数是相同的，则齿轮泵瞬时流量为：

(7)

式中，ω为齿轮角速度；B为齿宽；Ra，R分别为齿轮齿顶圆半径、基圆半径；f为齿轮啮合点到节点的距离。

齿轮在啮合过程中，其啮合点不断变化，因而啮合点与节点之间的距离f也发生变化，因此造成瞬时流量Qsh的变化[1]；2对齿同时啮合时，由于齿轮的端面间隙很小时，这2对齿之间的油液与吸、排油腔均不沟通，形成了封闭容积，随着齿轮的转动，此封闭容积会发生变化，使其中的液体受压缩或膨胀，造成封闭容积内液体的压力发生急剧变化[1]。将各工况下监测点压力变化、出油口流量变化分为过渡段(0～0.02 s)和稳定变化段(0.02～0.12 s)，对稳定变化段的数据进行后处理分析。图5为耳形、梯形卸荷槽在工况一、二、三、四下监测点1压力p1、监测点2压力p2变化曲线；图6为出油口流量变化曲线。出油口流量品质可用流量脉动系数来衡量[26]，其数学表达式为：

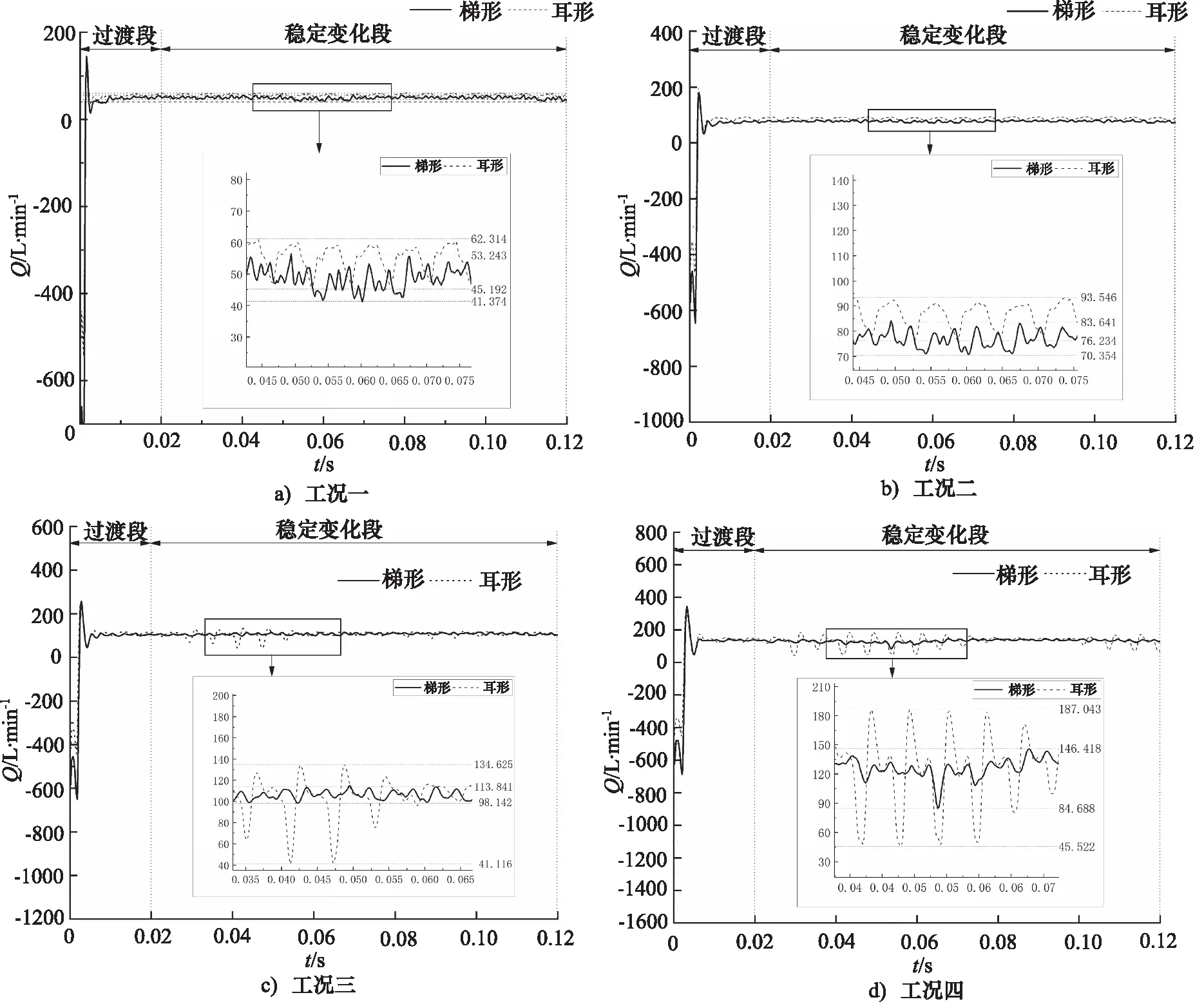
图6 不同工况下出油口流量变化曲线

(8)

(9)

图5a为工况一压力监测变化曲线，在稳定变化段，耳形和梯形卸荷槽在监测点1最高压力分别为1.537, 0.920 MPa，最低压力均为0.019 MPa；在监测点2，耳形卸荷槽最高压力为1.034 MPa，最低压力为0.743 MPa，梯形卸荷槽最高压力为0.923 MPa，最低压力为0.709 MPa；因此，梯形卸荷槽较耳形卸荷槽困油区最高压力在监测点1压力降低40.1%，在监测点2降低10.7%。同理得到，工况二困油区最高压力在监测点1压力降低47.5%，在监测点2降低19.2%；工况三困油区最高压力在监测点1压力降低40.4%，在监测点2降低22.5%；工况四困油区最高压力在监测点1压力降低36.3%，在监测点2降低17.7%。

图5 不同工况下监测点压力变化曲线

如图6a为工况一出油口流量变化曲线，在稳定变化段，耳形卸荷槽下出油口最大、最小流量分别为62.314, 45.192 L/min；梯形卸荷槽下出油口最大、最小流量分别为53.243, 41.374 L/min。因此耳形与梯形卸荷槽的流量脉动系数分别为0.296，0.250，流量脉动系数降低15.5%。同理得到工况二、三、四耳形与梯形卸荷槽的流量脉动系数分别为0.204，0.173, 1.064，0.148, 1.214，0.534；流量脉动系数分别降低15.2%,86.1%,56.1%。

图7为4组工况下监测点压力与出油口流量脉动系数降低数值比较。可以发现，工况一至工况四随着齿轮泵转速的增大，困油区监测点1与监测点2最高压力降低数值表现出先增大后减小的变化规律，出油口流量脉动系数降低数值也有相同的变化规律。由此说明，在齿轮泵某一种工况下，本研究设计的梯形卸荷槽可以有效降低困油区困油压力与出油口流量脉动。各组工况下降低困油区困油压力与出油口流量脉动的效果有所不一致，由此分析，梯形卸荷槽的槽深与降低困油区困油压力与出油口流量脉动的最佳效果具有匹配性。

图7 4组工况下监测点压力与出油口流量脉动系数降低数值比较图

4 结论

(1)本研究设计了一种具有更大卸荷槽面积、结构更加紧凑且易加工的梯形卸荷槽。梯形卸荷槽的线型轮廓由6条线段组成，包括4段直线段、1段φ4.0的圆弧和1段φ2.0的圆弧。其结构简单，构成的轮廓卸荷槽面积更大；

(2)通过比较4组工况下困油容积区监测点压力变化曲线可知，当转速在1000～4000 r/min内变化时，梯形卸荷槽结构能使困油容积区域监测点1的压力峰值比耳形卸荷槽降低36.3%～47.5%，监测点2降低10.7%～22.5%；能使出油口流量脉动系数比耳形卸荷槽降低20%～86.1%，证明了梯形卸荷槽降低困油压力缓解困油现象的高效性与降低出油口流量脉动的有效性，为渐开线外啮合齿轮泵卸荷槽的创新设计提供了一种新的途径；

(3)随着齿轮泵转速的增大，困油区监测点1与监测点2最高压力降低数值表现出先增大后减小的变化规律，出油口流量脉动系数降低数值也有相同的变化规律。