一组高考试题引发的思考

甘肃省兰州市第二十七中学 (730030) 陈鸿斌

1 问题呈现

问题1 (2020全国Ⅱ卷文21)已知函数f(x)=2lnx+1.

(1)若f(x)≤2x+c，求c的取值范围；

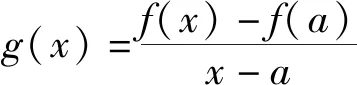
问题2 (2020天津卷20)已知函数f(x)=x3+klnx(k∈R),f′(x)为f(x)的导函数.

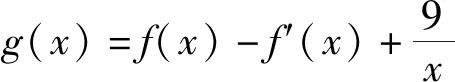
笔者发现问题1的第(2)问与问题2的第(2)问渗透了高等数学背景——Lagrange中值定理、以及函数的凹凸性. 以高等数学知识为背景命制高考题在十年前曾是个热点, 今年又重新体现, 而且有了新高度、 新角度, 推陈出新, 价值丰富. 虽然试题的设计来源于高等数学, 但是解决的方法仍是高中所学的数学知识, 对学生思维的逻辑性、抽象性以及学生的理解能力和自学能力提出了更高的要求, 着力考查数学核心素养.

2 高等数学背景解读

问题1和问题2的第(2)就具有《数学分析》[1]中“Lagrange中值定理”的背景．

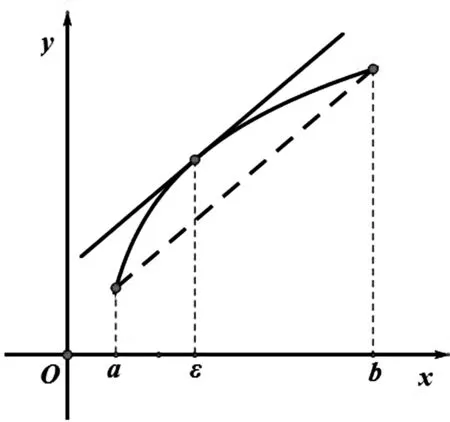
图1

几何意义：曲线在x=ξ处的切线与(a,f(a))和(b,f(b))的连线平行, 或者说, 曲线在x=ξ处的切线斜率与(a,f(a))和(b,f(b))的连线斜率相等. 如图1所示.

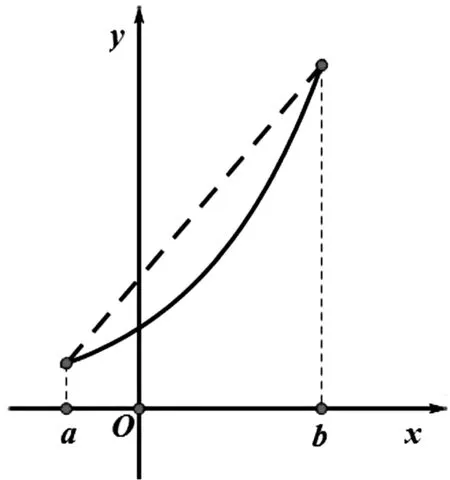
图2

问题2的第(2)还具有《数学分析》[1]中函数的凹凸性的背景．

定理设函数f(x)在[a,b]上连续, 在(a,b)内二阶可导, 则f(x)在[a,b]是凸的充分必要条件是∀x∈(a,b)有f″(x)≥0.特别地, 若此时在(a,b)中有f″(x)>0, 则f(x)在[a,b]是严格凸的.

几何意义: 曲线落在(a,f(a))和(b,f(b))的连线的下方. 如图2所示.

3 问题解答

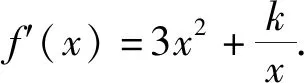
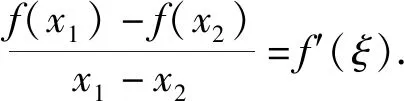
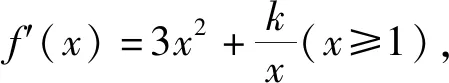
点评：上述问题主要考查函数的单调性、极值、最值、导数、含参不等式恒成立、不等式证明等基本知识, 考查数形结合、函数与方程、化归与转化等数学思想方法和分析问题、解决问题的能力. 作为一线的中学教师, 看到本题的表达形式, 应当要能够领悟命题者的设计意图, 背景来源于Lagrange中值定理、函数的凹凸性. 因此本题体现了高等数学与高中数学教学之间较好的衔接, 很好地考查了学生的学习潜能, 有利于高校选拔人才. 从笔者给出的中学解法和高等解法可以看出, 利用中学解法, 运算量大, 而且还要借助于第(1)问中所得结论才能实现第(2)的求解, 因此第(1)问的正确解答对第(2)问至关重要; 而利用高等解法第(2)就会变的独立, 通过Lagrange中值定理、函数凹凸性可以将问题进行转化, 使得运算量大大降低, 从而优化解题思路. 总之, 运用Lagrange中值定理、函数凹凸性求解上述题目的第(2)问, 比高考参考答案的解答简便许多, 换个角度, 将问题会看的会更加透彻.