从整体上探索发现和提出数学问题之途①
——以高中复习课“导数应用”为例
伍春兰 史红静
(1.北京教育学院 100120; 2.北京市通州区潞河中学 101149)
从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”),[1]已写入普通高中数学课程标准2017年版的课程目标中. 不争的事实是,中学数学课堂教学中,分析和解决问题的教学活动易寻,而学生在教师引导下发现和提出问题的活动难觅.
我们认为,把研究或处理的对象当作一个系统,研究系统、要素及环境三者的相互关系和变动的规律性,强调整体、联系、动态和最佳等观点.[2]不仅有利于分析和解决问题,更有助于发现和提出问题. 下面以高中复习课“导数应用”为例,呈现我们的教学思考、实践与反思.
1 现象描述
不等式及方程唯一解的证明,课堂上通常教师直接呈现命题,先粗略分析证明思路,就利用导数证明,最后是简单回顾. 其中,证明步骤可概括为四步:(1)构造新函数;(2)求导数找驻点;(3)(列表)分析;(4)结论. 例如,不等式ex≥x+1的证明、方程ex=x+1唯一解的证明,就是先构造新函数f(x)=ex-x-1,然后按上述步骤完成. 如果不易求出驻点,比如不等式ex>lnx+2的证明,教师会重点讲述如何利用“设而不求”的思想以解决问题. 即教学重点在于形成解决问题的套路,而命题是如何发现和提出的,命题之间有什么关系,数与形怎样结合,教学中鲜有问津.
2 学生调研
2.1 问卷设计
我们设计了四种前测试卷. 试卷1、3从指数函数f(x)=ex出发,考察与y=x+1、g(x)=lnx有关的可能结论. 试卷2、4从对数函数g(x)=lnx出发,考察与y=x-1、f(x)=ex有关的可能的结论.
每张试卷共有两大问题,问题(2)四张试卷都一样:请写出与f(x)=ex和g(x)=lnx有关的所有可能的结论. 试卷1、2的问题(1)提供了函数图象,试卷3、4的问题(1)给出了提问示例,见表1.
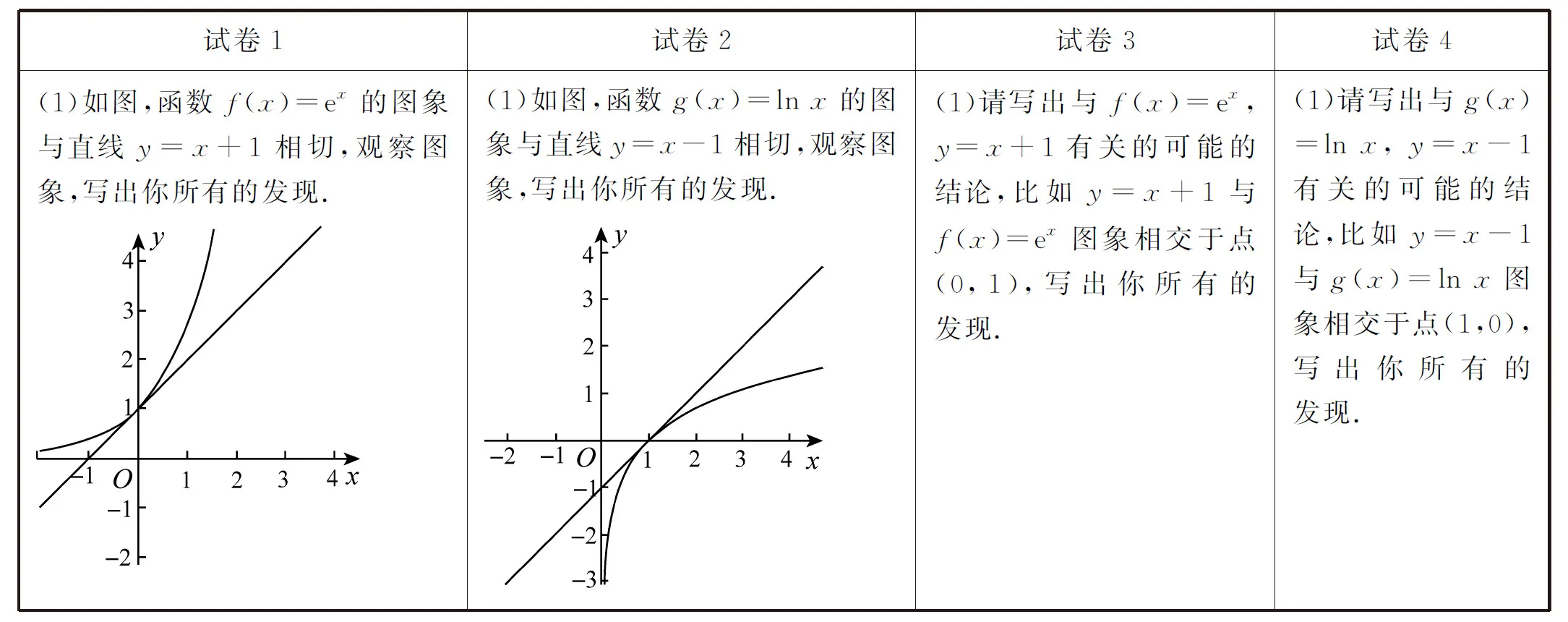
表1 四份前测试卷问题(1)
2.2 统计分析
参与前测的学生来自北京市某示范高中校普通班,共80人. 将学生分成水平相当的四个组,每组完成表1中的一种测试. 各试卷中问题(1)、(2)分别统计,其结果见表2、表3.

表2 各试卷问题(1)的反馈结果(%)的统计表
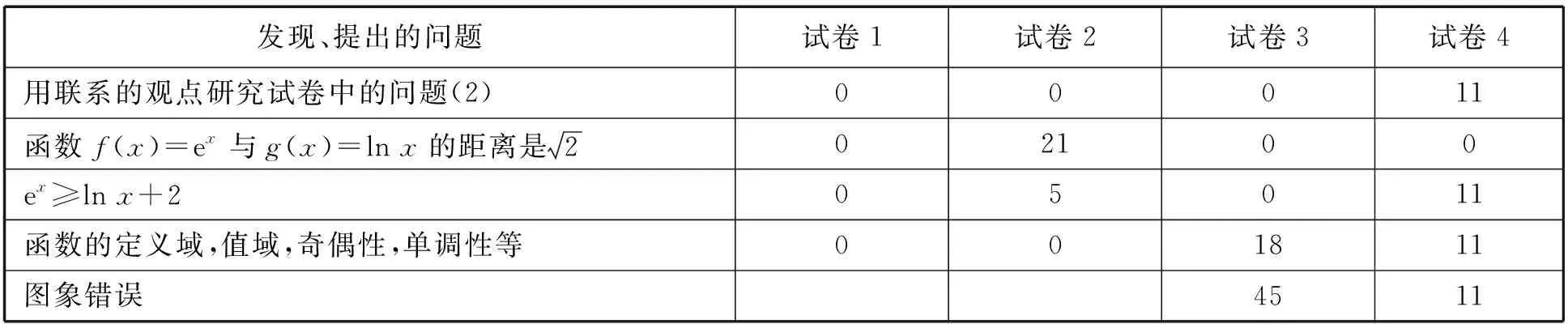
表3 各试卷问题(2)的反馈结果(%)的统计表
由表2和表3,我们获得了如下几条结论:
(1)准确的图形语言更容易让学生发现和提出有价值的数学问题.
(2)无论从指数函数还是对数函数出发,学生发现和提出新问题的结果相差不大(排除一位数学思维特别好的学生的影响因素).
(3)五成多(试卷有图)学生或不足一半(试卷无图)学生能提出恒成立问题(ex≥x+1),没有学生提出存在性问题(方程ex=x+1仅有唯一解x=0).
(4)能用数学符号语言描述数学问题的学生明显少于发现问题的学生比例.
(5)部分学生画图不准,影响了发现提出问题的质量. 还有部分学生即使图象画的准确或试卷给出,依然对图象中的数学关系视而不见.
(6)仅有几位学生提出不等关系ex≥lnx+2,虽然没有考虑到等号不成立情形.
结论(1)到(5)表明,不少学生由函数(图象)发现不等式问题,特别是方程问题的意识缺失,数学语言表达欠佳,也反映出我们教学的问题:仅重视不等式、方程唯一解问题转化为函数问题的求解证明,而由函数(图象)发现不等式、方程问题的逆向思考不足,数与形的系统思考及数学表达训练不够,特别是由形到数. 结论(6)、(7)显示部分学优生有较高的数学思考水平,以解题为目的教学将会压抑他们的发展. 如何将学生思维水平的差异转化为教学资源,如何使不同的学生数学思维得到相应的发展,都是值得关注的.
3 师生互动
基于学生的调研,课堂教学确定了两条主线:分别以指数函数f(x)=ex、对数函数g(x)=lnx为核心. 前者采用师生互动方式教学,后者选择学生合作交流方式教学. 下面仅呈现指数函数引发的教学活动片断.
3.1 对话不等式ex≥x+1的发现
教师先请提出此问题的学生Z说说怎么猜的?“看图象得到的”学生Z回复到,教师反问“我怎么看图没发现,你怎么一看就出来了”?“一开始我也没看出”学生Z说,“可后来我多看了几眼图象,发现除了点(0,1),函数f(x)=ex的图象全在直线y=x+1的上方,突然ex≥x+1就冒出来了,这让我很兴奋”. “为什么兴奋”教师追问,“因为我用数学语言描述了一个差点被我遗落的事实”学生得意地回答.
学生应该100%看到了这一现象(试卷1提供了函数图象,或试卷3学生自己画图准确的),但并不是所有学生能想到或能用数学语言表达,说明有意识用数学语言,特别是用符号语言思考并表达所见事实的数学眼光还需修炼.
3.2 剖析方程ex=x+1仅有唯一解的发现
在由函数“看出”方程的活动中,锤炼了学生数学的语言表达,也从整体上加深其对函数与方程关系的认识.
3.3 问道不等式ex >ln x+2的发现
不等式ex>lnx+2的发现是空白,只有几位学生提出:ex≥lnx+2,于是教师请其中一位学生A解释.“因为图中四条曲线(f(x)=ex、y=x+1、g(x)=lnx、y=x-1)只有这两条曲线(f(x)=ex、g(x)=lnx)之间的距离不明确,我很好奇,于是就用软件画出h(x)=ex- lnx的图象”学生A答道.“画图后,我发现h(x)的最小值大约是2.33. ”“这个做法很有启发:当遇到不明确的数学问题时,可以先借助软件画图,再去思考图形背后的数学原理. ”教师评价并继续追问:“接下来,你又做了哪些思考?”“我将前面两个不等关系ex≥x+1和lnx≤x-1变形为ex-1≥x和lnx+1≤x,再利用不等式的传递性可得ex≥lnx+2.”学生A欣喜地回答. “我们又一次试图用数学符号语言描述我们所看到的事实,这一次成功了吗?”教师向全班同学发问. 广泛的认同声中,学生B突然质疑道:“不等关系ex≥lnx+2,不就是h(x)=ex-lnx的最小值是2吗?这与画图结果矛盾!”学生A无法给出解释. 全体学生先是沉默,继而展开激烈讨论,声音此起彼伏. 同学C突然抢答道:“两个不等式等号成立条件不一样”沸腾的课堂瞬间安静了下来. 很快,C的想法在课堂上引起了共鸣. “这个不等关系如何提出更合理?”教师追问道,“去掉等号”学生们齐声回答“ex>lnx+2”.
学生初次提出问题遭受质疑,思维被数与形的矛盾结论羁绊,不得不再次思考数与形的精准性,突破瓶颈后获得了更有价值的问题,期间经历的磨练带来了更强烈的成功喜悦.
3.4 添加参数将问题拓展
学生知道引入参数可以提出动态问题,但初始提问的质量不高. 比如,在指数函数与线性函数关系的动态问题构建中(表4),学生仅从函数图象的位置关系角度提出了初始问题. 于是教师由不等式恒成立的角度提出求参数范围的示范问题,学生则从命题与逆否命题的角度模仿提出了新问题.

表4 指数函数与线性函数关系的动态问题构建
数学中的含参问题是学生普遍认为的难点,其关键在于学生读不懂题,不知道为什么有这样的问题. 通过动态问题的探究活动,学生运用“函数→图象→动态图→参数不等式、参数方程”的流程发现、提出问题,运用“参数不等式、参数方程→函数、图象”的流程证明问题. 理解了“含参问题”是如何演变得来的,学生自然也就不再困惑和束手无策了.
动态问题的提出是“由静到动”的创造性数学生成,它的求解和证明是“化动为静”的思维回归. 通过动态问题的发现、提出与证明,学生从系统的角度,对数学问题中的“动、静关系”“数形结合”思想的理解更加深刻.
4 若干思考
4.1 系统的整体观为发现和提出问题提供了保障
函数、方程、不等式及曲线密切相关,以系统的观点,特别是从其核心的整体观(整体—部分—整体)的反复雕琢,不仅理解了问题的来龙去脉,而且也从相异视角的考究中得到更多地发现, 达到开拓思路的目的,也为分析解决问题埋下伏笔.
4.2 系统的联系观为发现和提出问题搭建了平台
应用导数证明不等式及方程唯一解的问题,一般是作为导数应用“各自为政”. 教师突破以往给出的封闭题目,从指数函数、对数函数与线性函数的关系切入,创设了学生亲历“观察—抽象—探索—猜想—论证—反思”的完整过程的活动,特别是真正地把发现和提出问题的环节还给了学生. 学生经历了“画图不准确”的失败教训,“视而不见”的迷茫,不等式中“≥”的等号不成立的磨砺,沉淀下来都是宝贵的经验. 让那些出现问题的学生在错误痛点上发表看法,能够有效刺激学生的再思考,激发创造力.
4.3 系统的动态观为发现和提出问题拓宽了视野
动态问题的演化,给学生提供了更多地尝试发现、提出问题的机会. 联系“含参问题”“量词”“命题的否定”等知识,将已有的问题(静态)转化为求参数范围或取值(动态)的问题.
类似地,如果从连续函数离散化的角度,联系数列递推关系,我们还可以继续讨论,提出如下系列类似的问题:(1)若正项数列{an}中,a1=1,an+1=ean+an,则an≥2n-1; (2)若正项数列{an}中,a1=1,an+1=lnan+an+2,则an≤2n-1. 上述两个问题是怎样发现和提出的,可留作学优生课后思考. 并仿照它们的形式,提出更多有价值的问题,并给出相应的证明.

