奇异摄动Darcy-Stokes问题的非协调长方体元逼近*

周 萌，肖留超，王永俊

(河南工业大学)

0 引言

1 奇异摄动Darcy-Stokes问题

考虑奇异摄动Darcy-Stokes问题如下

(1)

(2)

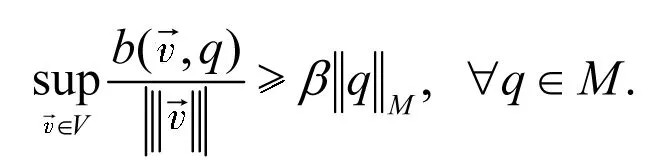
(6)

因此，问题(2)有唯一解[11].

(7)

其中

定义Vh上的离散模为

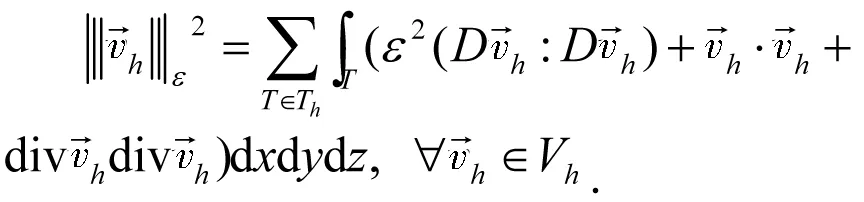
下面引进几个假定:

H1.divVh⊂Mh,

(8)

(9)

H3.存在插值算子∏h:V→Vh使

(10)

引理1 如果H1～H3成立，则下列式子成立

证明根据

(13)

引理1表明如果H1～H3成立，则ah(·,·)是强制的，bh(·,·)满足inf-sup条件，又因为a(·,·),bh(·,·)是连续的，所以离散问题(7)有唯一解[11]. 下面给出有限元逼近定理.

证明利用方程(1)、(7)和Green公式有，对∀wh∈Vh

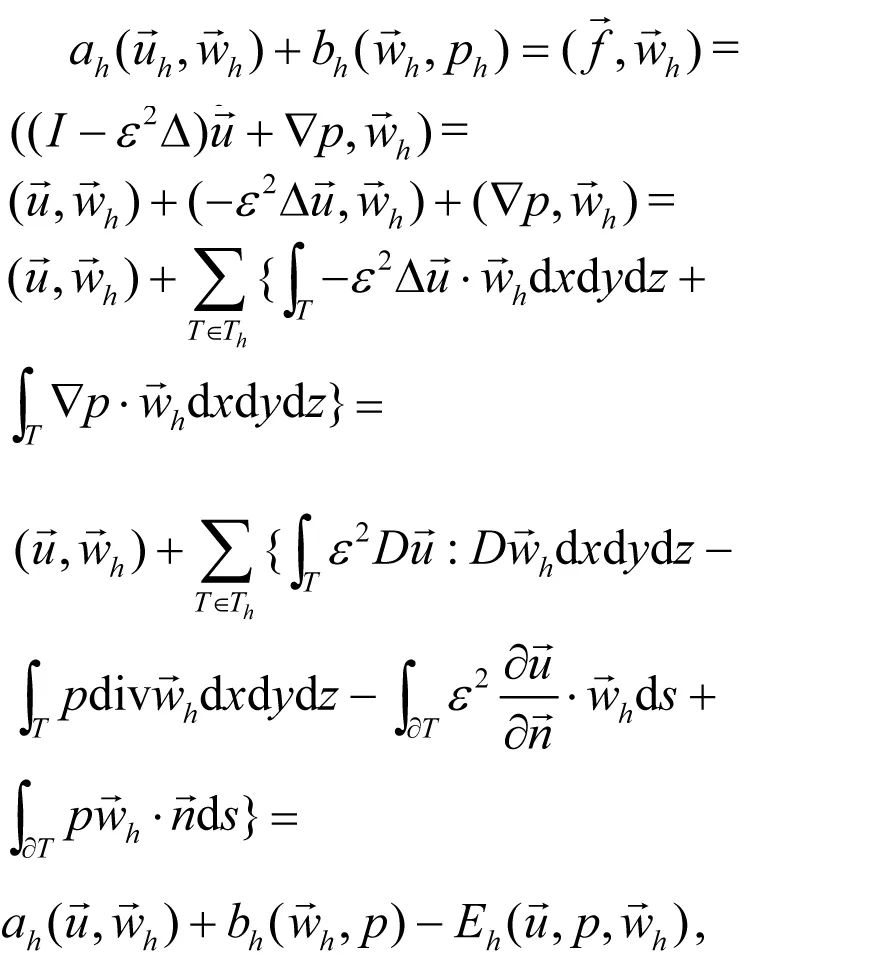
其中

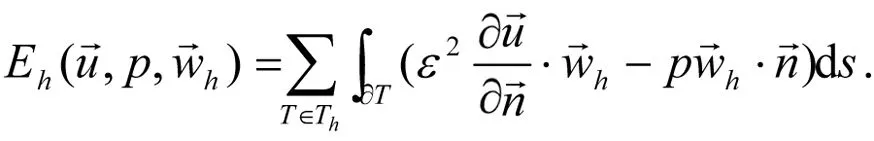
可得误差方程:

(15)

由

可得

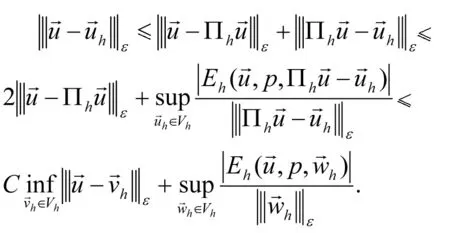
(16)

根据(12)式，有

则

由(16)、(17)式得

2 单元构造及误差分析

其中

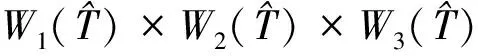
自由度取为

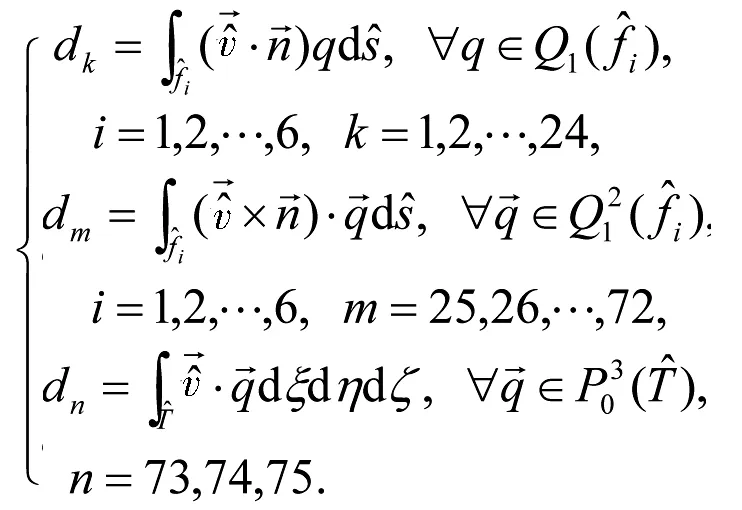
(20)

易知自由度的维数和形函数空间的维数相同.

引理2 (20)式中的自由度可以唯一确定空间(19)式中的元素.

(21)

经计算矩阵M93×93是可逆的，可知单元构造是适定的.

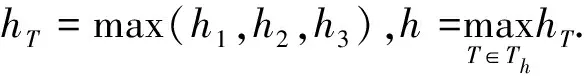
单元T上的形函数空间定义为:

(22)

定义速度和压力的两个有限元空间分别为:

根据有限元空间Vh,Mh的定义，可得条件H1～H3成立，所以离散问题(7)有唯一解，且有如下估计结果.

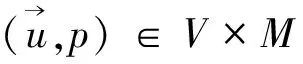
(23)

其中正常数C与h无关.

证明根据定理1，首先给出逼近误差估计.

(24)

(25)

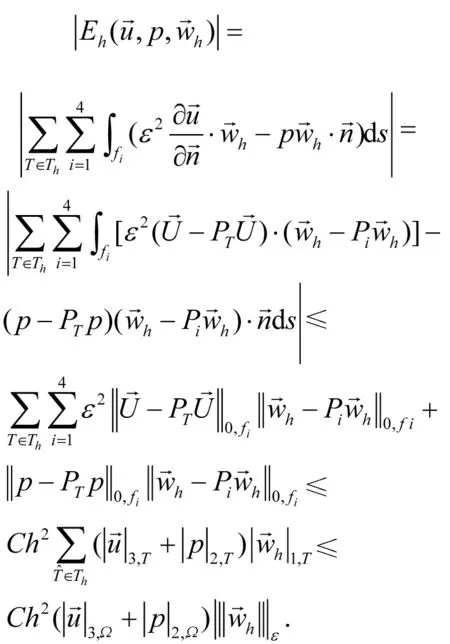
(26)

将(24)、(25)、(26)代入(14)可得(23)成立. 定理得证.