基于主成分分析法对承运线路定价的计量分析*

朱家明，尹俞苹，曹迎春

(安徽财经大学)

0 引言

无车承运人是指公路货运市场以承运人的名义承揽货源,与货主方签订运输合同,然后无车承运人将货源外包给实际承运人,并与实际承运人签订运输合同,由实际承运人按照无车承运人的要求完成运输服务，董娜最早对国内无车承运人的内涵、优势等进行分析, 提出了中国发展无车承运人的相关建议[1]；黄少波、李挥剑从经济社会、交通运输行业发展等方面,论述了无车承运在中国发展的必要性与可行性[2]；常连玉、陈海燕通过建立无车承运人运力资源组织优化模型，对运力资源、货源和运输线路进行了匹配优化[3]；张冰清对无车承运人在发展中存在的问题进行了探讨,并根据实际情况给出了发展对策[4]；金邹苹在综合国内外承运人平台研究现状的基础上,采用动态规划算法求解得最优序贯拍卖策略[5]；华芬通过分析得到了通过风险预警机制的建立等可以提高平台的抗风险能力的结论[6]；汪琼枝、马永传提出了一种新的基于CART决策树的无车承运人平台货运任务定价模型[7]；陈煜婧、杨斌分析了处于不同发展阶段的无车承运人在3种因素作用下对道路运输市场结构的影响[8]；李雯等构建三维度的无车承运人物流风险管理WSR方法[9].随着中国无车承运行业的逐步兴起，承运线路的科学定价问题也成了众多无车承运人平台亟待解决的问题.要想解决承运线路的定价问题就要快速促进成交和采用较低的承运成本，因此该研究以无车承运人的视角，暂不考虑面向货主的运输任务的报价，通过建立数学模型，为科学决策提供定量依据.

1 数据来源与假设

数据来源于2020年MathorCup高校数学建模挑战赛A题，为便于解决问题，提出以下几条假设：⑴假设所收集的数据真实可靠；⑵不考虑通货膨胀对承运线路定价的影响；⑶假设不考虑特殊情况(比如天气、路况等异常)对计划时间的影响；⑷假设各项运杂费短期内不会发生变化；⑸假设车辆运输途中没有损耗.

2 无车承运线路定价影响因素分析

2.1 研究思路

该文通过查阅相关资料及文献，对无车承运平台的运作模式进行分析，无车承运人以承运人身份与托运人签订运输合同，承担其相应的责任和义务，通过委托实际承运人来完成运输任务，其收入来源主要是规模化的“批发”运输而产生的运费差价.无车承运平台作为受托方被实际承运人委托，开展运输业务，其运作模式如图1所示.

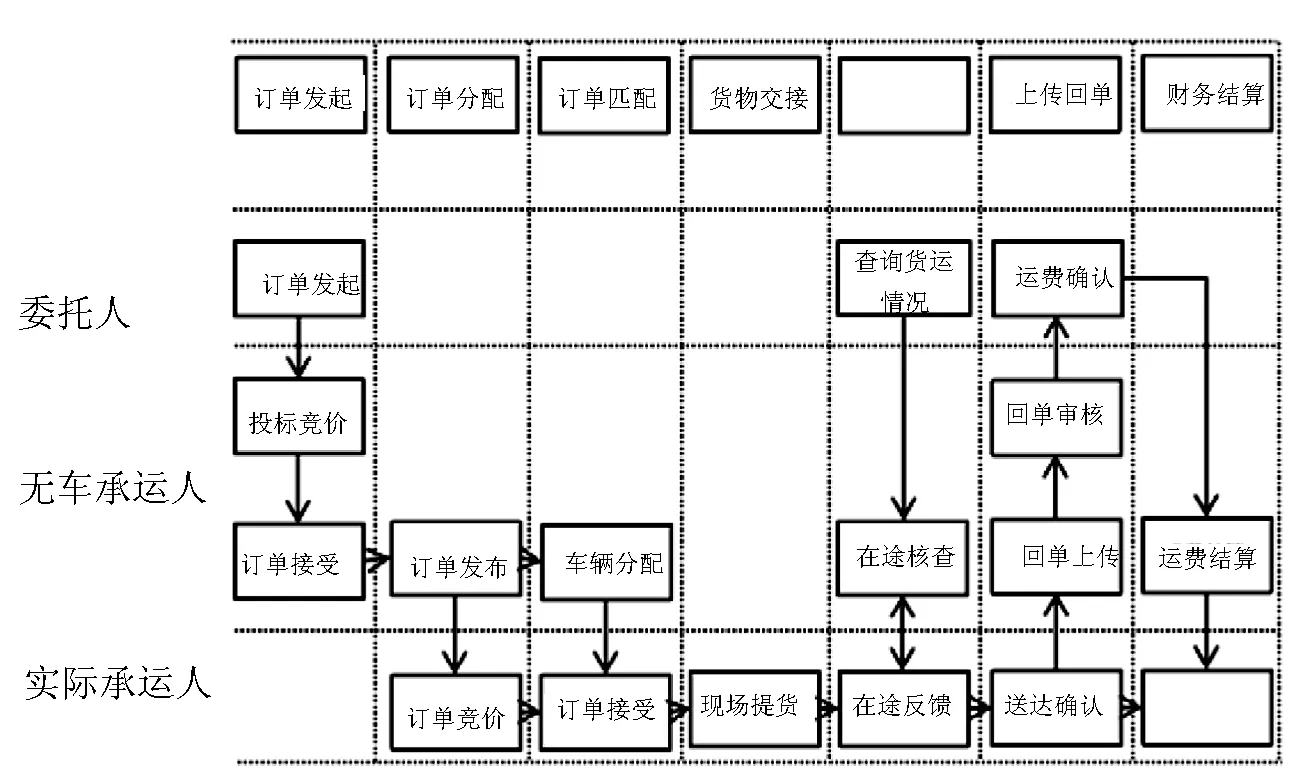
图1 国内无车承运运作模式流程图

在“国内无车承运运作模式流程图”中，不同因素如总里程、线路总成本、线路指导价等均有可能在一定程度上影响货运线路的定价.若选择用这些指标建立适当的模型并且对模型进行验证，从科学的角度定量分析则可以确定影响承运线路的主要因素，从而解决无车承运人平台以较低的承运成本运营的定价问题.在对题中所给数据进行分析及预处理后，剔除数据中由于误差或潜在的特殊因子而导致的无效数据及无用变量，运用主成分分析法对模型进行求解，通过比较不同指标推导出影响无车承运人平台进行货运线路定价的主要因素，最后通过KMO和Bartlett球形度检验值对模型进行检验.

2.2 研究方法

(1)数据处理与模型建立

为了便于分析，消除各项指标数据量纲的影响，该文对题目所给数据中业务类型、需求类型2、是否续签、标的展示策略、打包类型、运输等级、调价类型、调价紧急程度、地区类型、需求紧急程度这10个变量进行标准化处理，剔除变量线路总成本中的8组无效数据，并去除如子包号、装卸的次数、装的次数等无用变量，处理公式为:

(1)

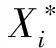
为考察原有变量是否适合进行主成分分析，选取变量总里程、线路总成本、线路指导价(不含税)、线路价格(不含税)、车辆吨位、运输等级、标的展示策略、是否续签、调价比例、线路编码、业务类型、调价类型、需求类型2、打包类型、需求紧急程度、B端议价反馈数量、C端议价反馈数量导入SPSS软件进行主成分分析.根据Kaiser常用的度量标准，KMO>0.9表示非常合适; 0.8表示合适; 0.7表示一般; 0.6表示不太合适;0.5以下表示极不合适[10].KMO值越接近于1，意味着变量间的相关性越强，则原有变量更加适合作主成分分析[11]，通过代入变量比较分析，得到了KMO最大的一组变量，KMO值为0.802，Bartlett球形检验的Sig值接近于0.000，这表明选取的指标间具有很强的相关性，数据极具代表性(见表1).

表1 KMO 和 Bartlett 检验

用x1,x2,…,x17表示17个影响无车承运人平台进行货运线路定价的主要因素，c1,c2,…,c17表示各影响因素的权重，那么加权之和为：

s=c1x1+c2x2+…+c17x17

(2)

设x1,x2,…,x17表示以x1,x2,…,x17为样本观测值随机变量，找到c1,c2,……,c17使

Var(s=c1x1+c2x2+…+c17x17)

(3)

的值达最大.限制约束条件：

(4)

寻找其他主成分，使两个主成分协方差为0，设zi表示第i个主成分，i=1，2，…，17，可设

(5)

对每一个i，均有

(6)

且[ci1+ci2+…+ci17]使Var(zi)的值达到最大.

(2)模型的求解与验证

将数据导入SPSS求解得到碎石图(如图2所示)，通过观察特征值的碎石图来确定因子数，由图2可知，前4个特征值较大，第6个以后的特征值均较小，图形较平缓.因此，选取前6个因子，即无车承运人平台主要影响因素有总里程、线路总成本、线路指导价(不含税)、线路价格(不含税)、运输等级、车辆吨位.

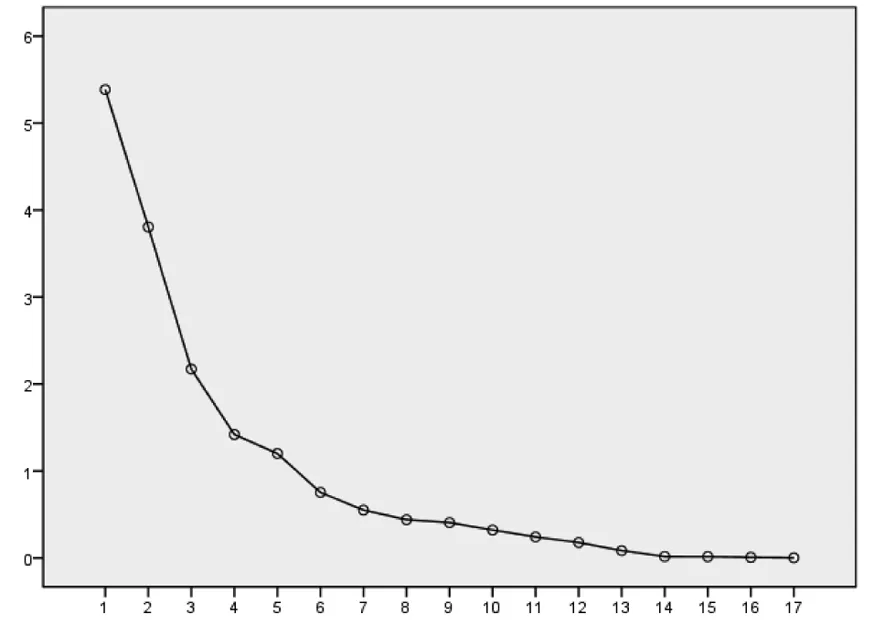
图2 碎石图

对上述结果进行KMO和Bartlett球度检验(见表2)，结果显示KMO值为0.909，Bartlett球形检验的Sig值接近于0.000，即模型通过检验.

表2 KMO和Bartlett 检验

3 已成交线路历史定价的评价

3.1 研究思路

通过上述分析研究思路如图3所示，根据层次分析法对各定价因素的重要程度进行两两比较，选择德尔菲法对定价因素的重要程度进行多轮专家调查来确保较高定价的市场灵敏度[11].通过查阅和参考相关文献对各类型因子进行参数设置，确定各因素重要程度的量化值来构建两两比较矩阵，并且通过计算得到各定价因素的优先级.最后，通过对矩阵的一致性检验排除由两两比较的判断标准不同而导致的系统性误差，并进一步进行分析得出问题结论.

图3 研究思路图

3.2 研究方法

(1)模型建立

常用的定价方法有成本导向定价法、供需关系定价法、竞争导向定价法、服务差异定价法等[12]，但这些模型均为单一因素定价模型，故而选择基于多因素的符合定价方法，即层次分析法.运用层次分析法确定总里程、线路指导价(不含税)、线路总成本、运输等级、车辆吨位等因素在定价中的优先级和权重，从而为线路定价提供参考.

两两比较是层次分析法应用的基石，对总里程、线路指导价(不含税)、线路总成本、运输等级、车辆吨位等定价因素的重要程度进行两两比较，并根据重要程度的量化值(见表3)[11]，得到各定价因素重要程度的两两比较结果(见表4).为使定价的市场灵敏度更高，选择德尔菲法对定价因素的重要程度进行多轮专家调查排序.

表3 重要程度的量化值

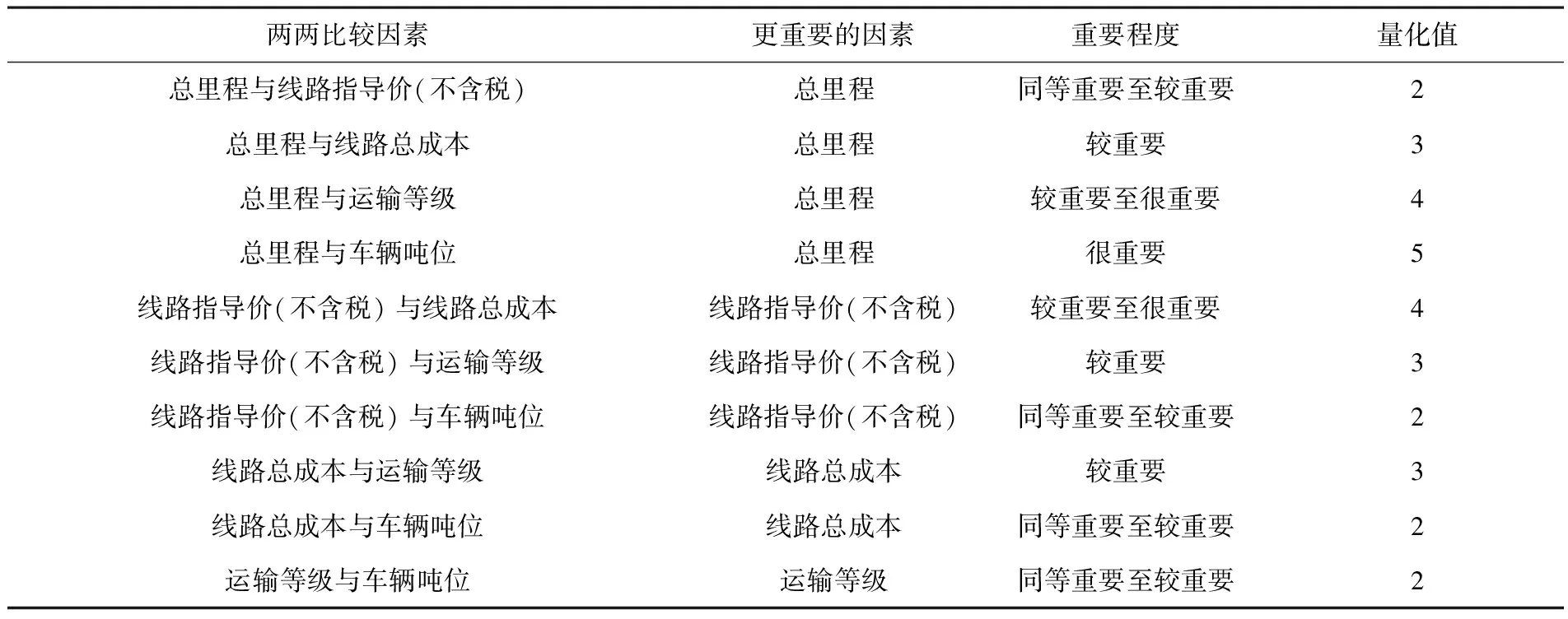
表4 基于德尔菲法的各定价因素重要程度两两比较结果

为构建由各定价因素重要程度的两两比较结果组成的矩阵，需要确定各定价因素的优先级，首先以表4中“更重要的因素”为指引[13]，在两两比较矩阵中输入各因素重要程度的量化值，如果各定价因素在与自身相比的情况下，其重要程度的量化值为1，定价因素重要程度两两比较矩阵见表5[11].

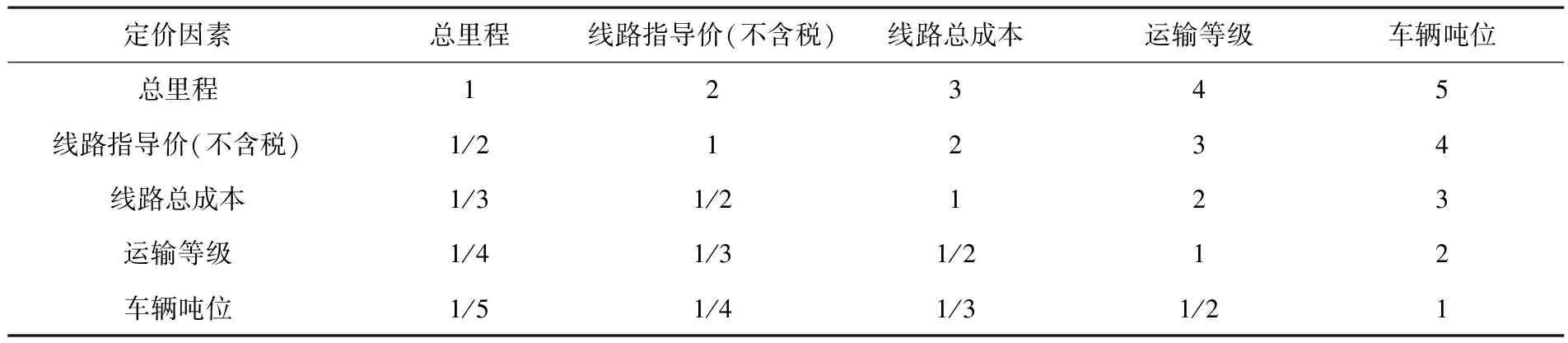
表5 定价因素重要程度两两比较矩阵

为确定各定价因素的优先级，首先计算两两比较矩阵中每一列数值之和然后将两两比较矩阵中的每项数值除以其所在列的数值之和[14]，得到标准两两比较矩阵(见表6)；最后计算标准两两比较矩阵中每一行数值的算术平均数，得到各定价因素的优先级(见表7).经计算，总里程以0.416212445成为最重要的因素，线路指导价(不含税)以0.261787988排第二，线路总成本以0.161050407排第三，运输等级以0.098572773排第四，车辆吨位以0.062376387排第五.

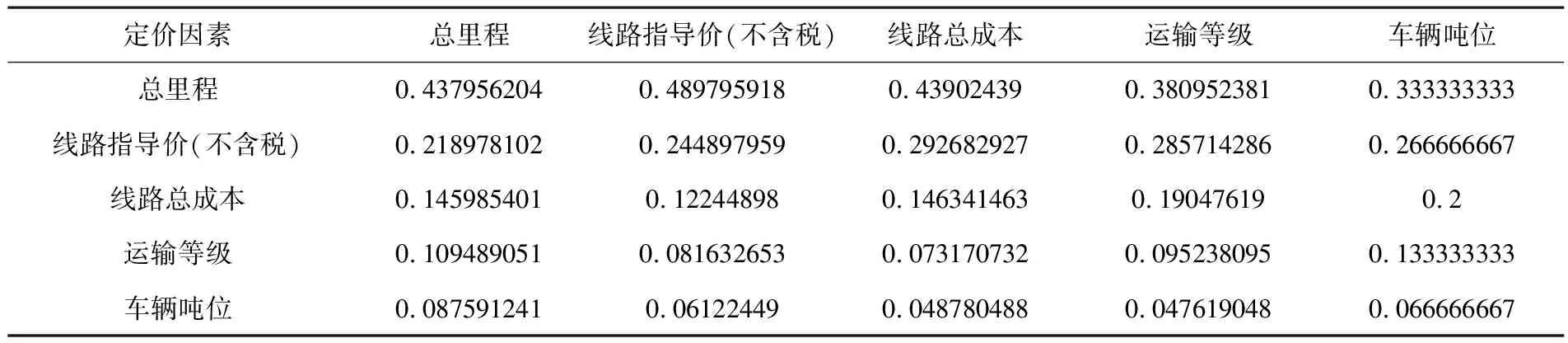
表6 定价因素重要程度标准两两比较矩阵

表7 定价因素优先级

(2)模型求解

由于在层次分析法中，两两比较的判断标准不一定相同，所以允许存在一定程度的误差.一般情况下，若一致性比率小于或等于 0.1，则认为判断矩阵通过一致性检验；否则，认为判断矩阵不具一致性[13].

将两两比较矩阵中的所有列与相应的优先级相乘，计算各行数值之和，得到权向量[13]：

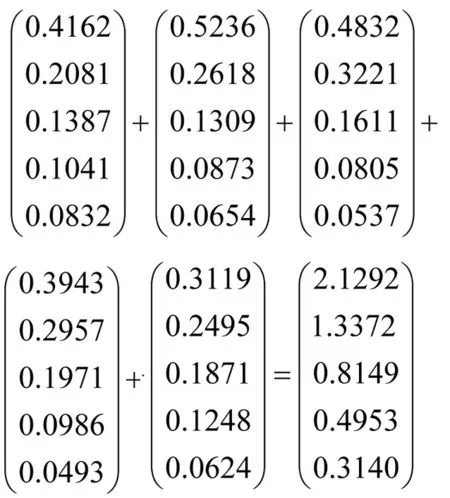
(7)

将得到的权向量除以相应的优先级结果见表8.

表8 权向量除以相应的优先级

计算出上述数值的平均数

λ=5.068323222

(8)

计算一致性比率，即

CR=CI/RI

(9)

其中：一致性指标

CI=(λ-n)/(n-1)=0.017080806

(10)

随机一致性指标RI的值取决于比较项目的数量，该文选取的定价因素有5 个，故RI=1.12(见表9).经计算得到

表9 随机一致性指标RI值

CR=0.015250719< 0.1

(11)

所以一致性程度符合要求，说明上述判断结果有效.

通过上述对历史定价数据的分析可知，总里程是线路定价的首要考虑因素，线路指导价(不含税)、线路总成本、运输等级、车辆吨位等为次要因素.所以通过分析得出：已成交线路历史交易数据中的定价较为合适.

4 承运线路的调价策略研究

4.1 研究思路

对承运线路的调价策略制定问题，选取合适因素作为自变量，对因变量进行回归分析来检验拟合优度以及检验是否存在序列相关问题.根据回归分析建立线性方程，以此计算出一次报价、最终定价和总成本，通过上述分析得出调价策略.

4.2 研究方法

(1)模型建立

选取运输等级、总里程、车辆吨位作为自变量，并对作为因变量的线路价格(不含税)、线路指导价(不含税)以及线路总成本进行回归分析.R2表示回归的拟合程度，越接近1说明拟合得越完美，而D-W值是衡量回归残差是否序列自相关，如果严重偏离2，则认为存在序列相关问题.

回归结果见表10～12，三组自变量均为运输等级、总里程、车辆吨位，第一组的因变量为线路价格(不含税)，R2为0.979，D-W值为1.996；第二组的因变量为线路指导价(不含税)，R2为0.982，D-W值为2.007；第三组的因变量为线路总成本，R2为0.994，D-W值为1.987.综上，三组数据回归的拟合程度都很高，并且不存在序列相关问题.

表10 第一组回归分析表

表11 第二组回归分析表

表12 第三组回归分析表

(2)模型求解

根据回归分析建立线性方程，假设：

Yi=C(1)×X1+C(2)×X2+C(3)×X3

(12)

Y为因变量、线路总成本(Y1)、线路价格(不含税)(Y2)、线路指导价(不含税)(Y3)，X1为总里程，X2为车辆吨位，X3为运输等级.计算得到各系数，最终方程为：

Y1=4.4073×X1+5.5988×X2+34.3916×X3

(13)

Y2=5.9247×X1-0.2125×X2+

34.3940×X3

(14)

Y3=4.5719×X1+5.8037×X2+24.6734×X3

(15)

通过上述回归方程可计算承运线路平台的第一次报价、最终定价和总成本数据.

(3)四维图形

根据三元一次回归方程，通过MATLAB编程得到图形，将数据可视化，结果如图4所示.

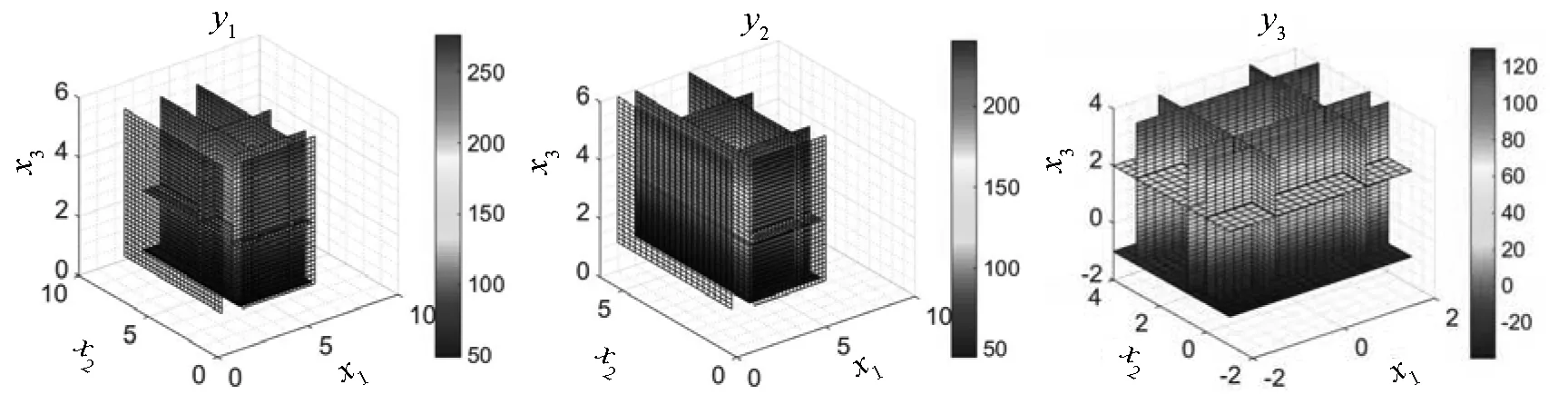
图4 回归结果图

(4)调价建议

在数据处理中，R2和D-W值都是符合较高拟合度的，所以有理由认为定价方式是合适的.关于调价策略，基于市场交易，认为平台调价策略应该为一二三次报价逐渐升高，并根据紧急程度确定报价升高的程度确定最终定价.

5 结束语

综上所述，该文运用主成分分析法、层次分析法等方法对所收集的已成交货运线路历史交易数据进行定量分析，最终得出影响货运线路定价的6个主要影响因素为：总里程、线路总成本、线路指导价(不含税)、线路价格(不含税)、运输等级、车辆吨位.而首要影响因素为总里程，而这一结论与已成交线路历史交易数据相吻合，说明了该文研究方法的科学性与合理性.同时，在已有的定价方式的基础上，利用已经证实的6个影响因素，通过构建三元一次回归模型对原有定价方式进行匹配优化，进而得到了平台一二三次报价应该逐渐升高，并根据紧急程度确定报价升高的程度确定最终定价的新的调价策略，通过对回归拟合程度及序列自相关的结果进行分析，可以认为此调价策略是较为合理和科学的，在一定程度上可以为无车承运人平台定价提供科学的决策依据.