分数阶多点边值问题的再生核数值方法*

万 策，周永芳

(河北工业大学)

0 引言

考虑以下分数阶多点边值问题

(1)

其中p(t),q(t),f(t)为给定的函数，m为正整数, 0<ξi<1,Dv为Caputo分数阶导数

(2)

方程(1)解的存在性和唯一性已在文献[1-2]得到证明.

分数阶边值问题在物理学、化学、空气动力学、信号处理等领域中有着重要的应用. 由于分数阶边值问题广泛的应用背景，分数阶边值问题引起人们浓厚的兴趣. 对于分数阶边值问题，学者们致力于解的存在性等性质的研究[3-6]. 由于分数阶导数的复杂性, 使得求解分数阶边值问题十分困难, 因此给出行之有效的数值方法显得尤为重要. 目前, 已有许多学者提出求解分数阶边值问题的数值方法，如：光谱法[7]、有限元法[8]、 外推法[9]、有限差分法[10].

近年来，再生核空间理论得到迅速的发展, 再生核数值方法已成为数值分析的有效手段之一，许多学者利用再生核数值方法求解分数阶边值问题. 耿发展研究了求解非局部边值问题的再生核算法[11];李秀英使用再生核数值方法求解变分数阶微分方程，该方法只需较少的节点即可获得高精度的数值解[12];吴勃英基于再生核理论简化了再生核函数的形式，提出了简便且高效的数值算法[13];Jiang和Arqub运用再生核数值方法求解时间分数阶偏微分方程, 并分析了近似解的稳定性和收敛性[14-15].

目前再生核算法对于两点边值问题的数值求解较为成熟，但对于多点边值问题的研究不够深入, 其原因是使用传统的再生核方法获得满足多点边值条件的再生核函数过程是繁琐的，且得到的再生核函数形式十分复杂. 针对这一问题，该文通过移位Jacboi多项式获得满足多点边值条件的再生核函数，与传统再生核数值方法相比，获得的再生核函数是多项式形式，使得计算更为便捷.数值结果表明该方法具有较高的精度.

1 预备知识

1.1 移位Jacboi多项式

定义在区间[0,1]上的移位Jacboi多项式可由以下递推公式得到

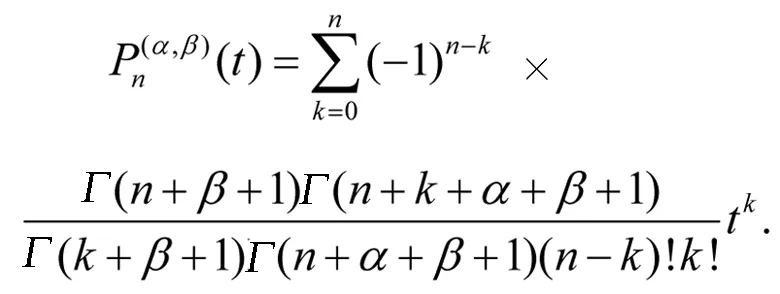
(3)

正交性条件

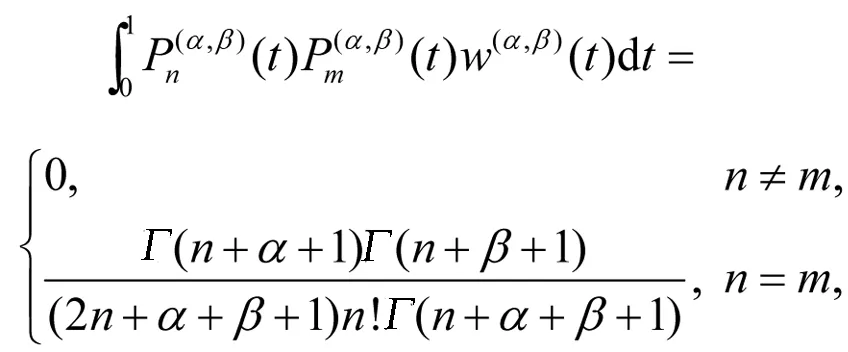
(4)

其中w(α,β)(t)=tβ(1-t)α.

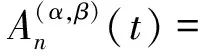
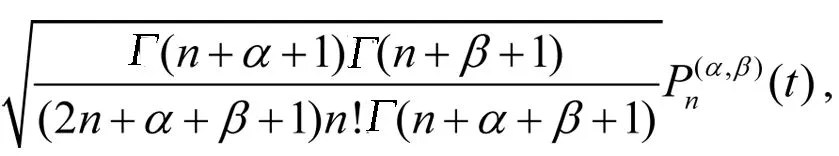
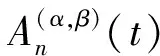
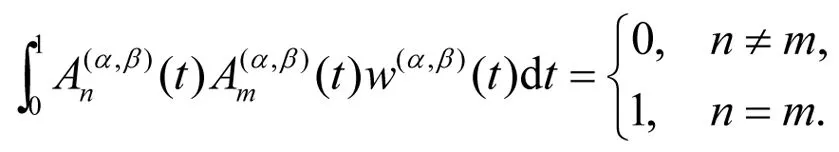
(5)

1.2 再生核空间的构造

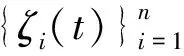
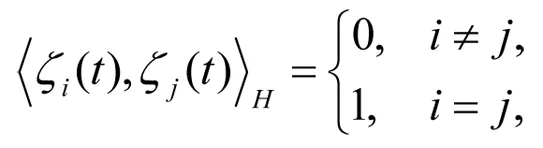
这里t∈X，X是一个紧集，那么对于任意固定的

s∈X,H的再生核函数具有以下形式

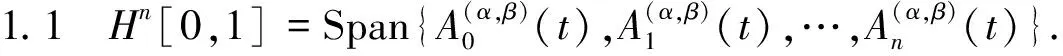
易知Hn[0,1]是希尔伯特空间，内积为

范数为

定理1.2Hn[0,1]的再生核函数为

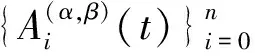
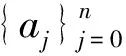
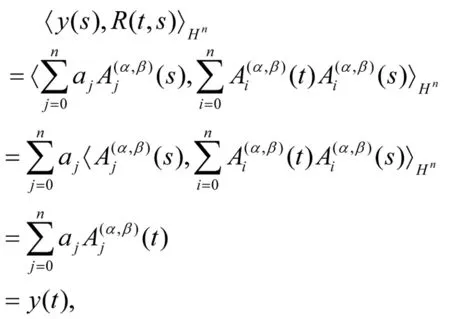
可得R(t,s)是Hn[0,1]的再生核函数.

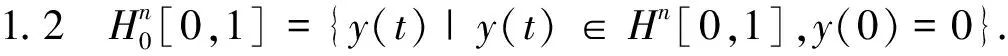
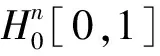
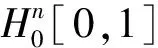
“基于此，后勤运营风险的有效控制必须依靠科学的风险管理方法。”沈崇德表示，科学的风险管理体系可以帮助每位后勤员工识别、判断工作中发生风险的可能性，增强风险防范意识，提高应对突发风险的能力。

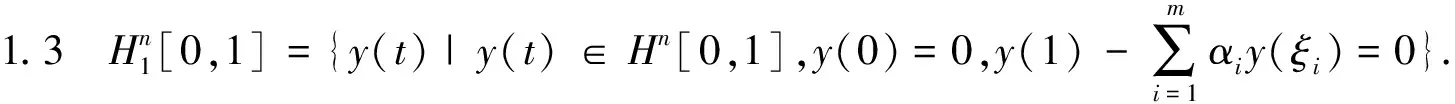
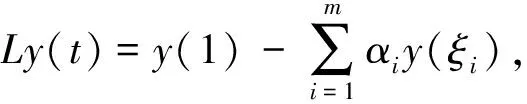
这里Lt的下标t表示算子L作用于t.

2 配置法

令Ay(t)=Dvy(t)+p(t)y′(t)+q(t)y(t),易得A是有界线性算子，则方程(1)可转化为以下算子形式

(6)

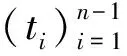
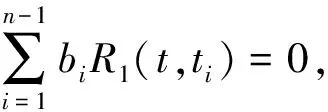
则

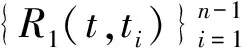
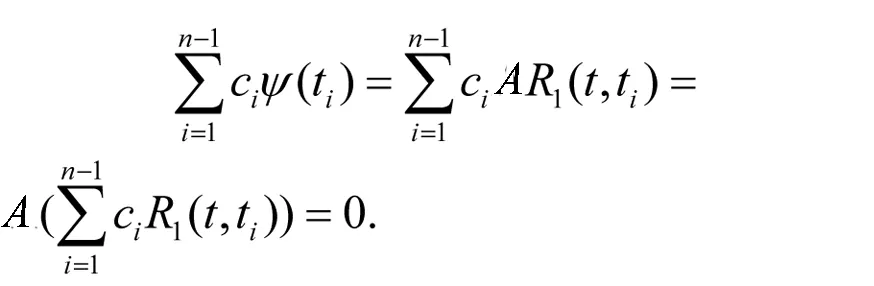
因为方程(1)解是唯一的，故算子A是可逆的，则有

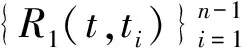
证明成立.

方程(1)的近似解yn(t)可表示为

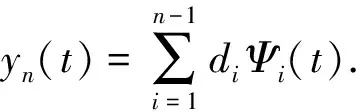
(7)

将式(7)代入式(6)，可得

则有

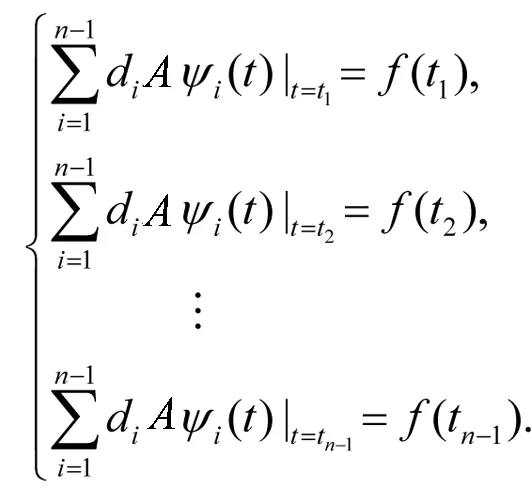
(8)

方程组(8)可简化为矩阵形式

Bd=f,

(9)

其中B=(bij)为n-1阶可逆方阵,

bij=AΨi(t)|t=tj,d=(d1,d2,…,dn-1)T,

f=(f(t1),f(t2),…,f(tn-1))T.

则有

d=B-1f

(10)

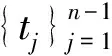
‖ξn(t)‖∞=‖y(t)-yn(t)‖∞≤Mhn-1,

3 数值算例

例1 考虑以下线性分数阶多点边值问题[11,17]

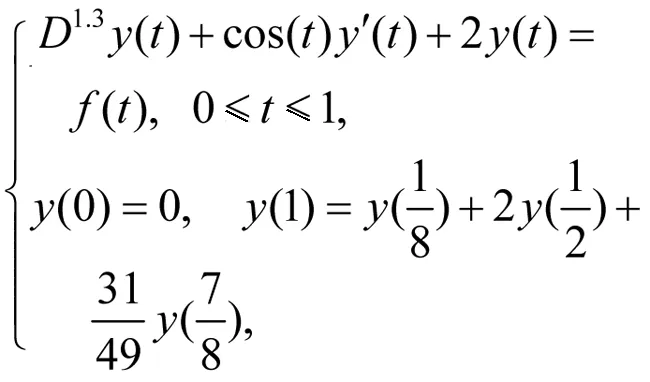
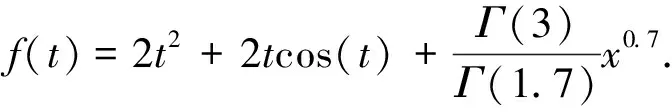
表1 例1的绝对误差

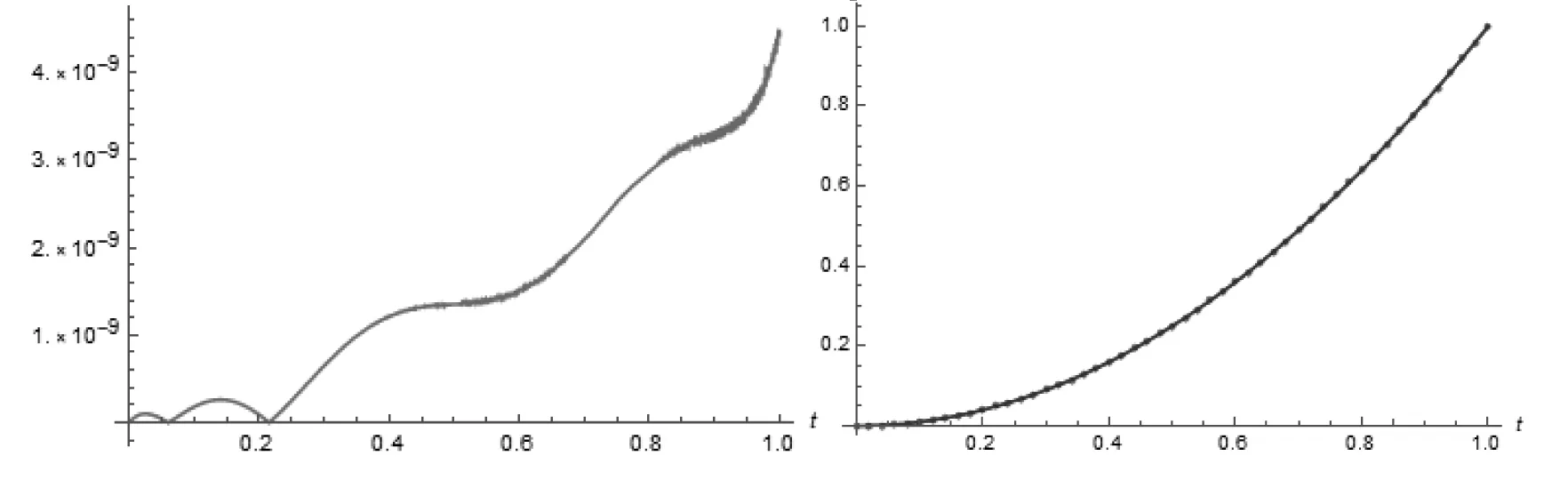
图1 例1中|y7(t)-y(t)| (左)及近似解y7(t) (点)与精确解(线)y(t) 的比较(右)

例2 考虑以下线性分数阶多点边值问题

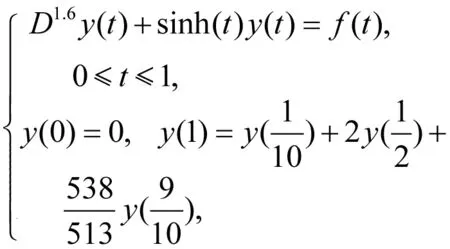
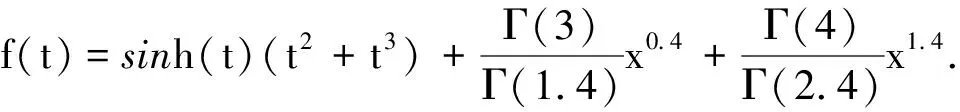
表2 例2中近似解y7(t)的绝对误差