基于BP神经网络的海洋温度预测及鱼群迁移方向研究*

杨 敏，白怡坤，刘 静，王 薇，祝颖莲

(嘉兴学院)

0 引言

随着全球变暖，海洋环境也发生着变化，进而影响着某些海洋生物的栖息地，一些物种会迁移到适合它们生活和繁殖的地方.美国缅因州的龙虾种群就是一个例子，他们正缓慢地向北迁移到海洋温度低一些的加拿大.海洋环境的变化使得渔业资源开发环境发生了变化.该文基于2020年美国数学建模竞赛A题，研究全球温度升高对苏格兰北大西洋鲱鱼和鲭鱼的栖息地影响.鲱鱼和鲭鱼对苏格兰的渔业经济有着重要贡献，这两类鱼群位置的变化对一些小的渔业公司尤其重要，因为一般小公司的渔船上没有冷藏设备，无法进行远程捕鱼；或者即使进行远程捕鱼却无法盈利.该文通过海水温度垂直变化得到鲱鱼和鲭鱼适宜生活的水温的范围，再由BP神经网络模型预测未来50年的温度变化情况.根据温度变化情况搜索适宜水温范围所在的经纬度，得到鱼群在未来50年内最有可能出现的位置.

1 苏格兰附近的海水温度分析及处理

该文采用的数据是从NOAA气候诊断中心(NOAA Climate Diagnostics Center) 获取[1].

截取数据为苏格兰北大西洋北纬55.5°到北纬64.5°，西经168.5°到东经5.5°(N55.5°～64.5°,E-11.5°～5.5°)的范围，空间分辨率：1°×1°，具体数据为1990～2019年每周的表层水温.

苏格兰附近存在3处渔港，分别为彼得黑德(Peterhead)，位置为(57.3021°N,1.4753°W)；设得兰群岛(Shetland)，位置为(57.4115°N,2.0106°W)；弗雷泽堡(Frserburgh)，位置为(57.4115°N,2.0106°W).彼得黑德(彼得黑德与弗雷泽堡距离相近)与设得兰群岛两处渔港附近的四季海洋表层水温范围如图1所示.

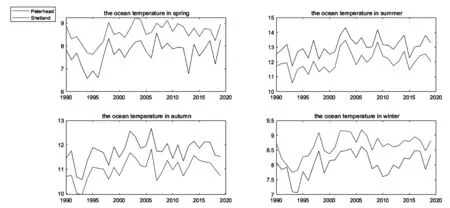
图1 苏格兰附近海域不同季节对应的气温变化图

查阅鲱鱼与鲭鱼的生活习性，可知鲱鱼适合在水深25～200 m，水温 10 ℃以内的环境中生长[2]；鲭鱼属于中上层鱼类，暖水性，基本上在水深50～200 m左右生长，5 ℃以下可致死[3].通过两种鱼的活动海域和活动水深可以发现，这两种鱼的生活习性大致相同.所以可以将这两种鱼的鱼群视为同一鱼群来进行研究.研究时选取水深200 m，适宜温度取7.5～9 ℃.

考虑海水深度与温度满足线性关系，海水的温度T随深度(H)的增加而降低，每深1000 m，下降1.5 ℃[4]，即

(1)

如图2所示，利用热力图描述2019年春夏秋冬4个季节海水在200 m处温度鱼群分布.其中星号表示鱼的位置.

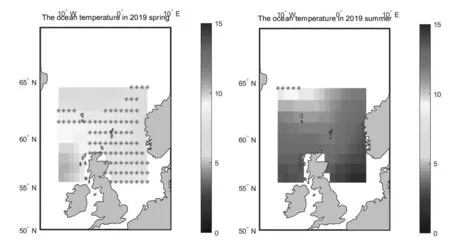
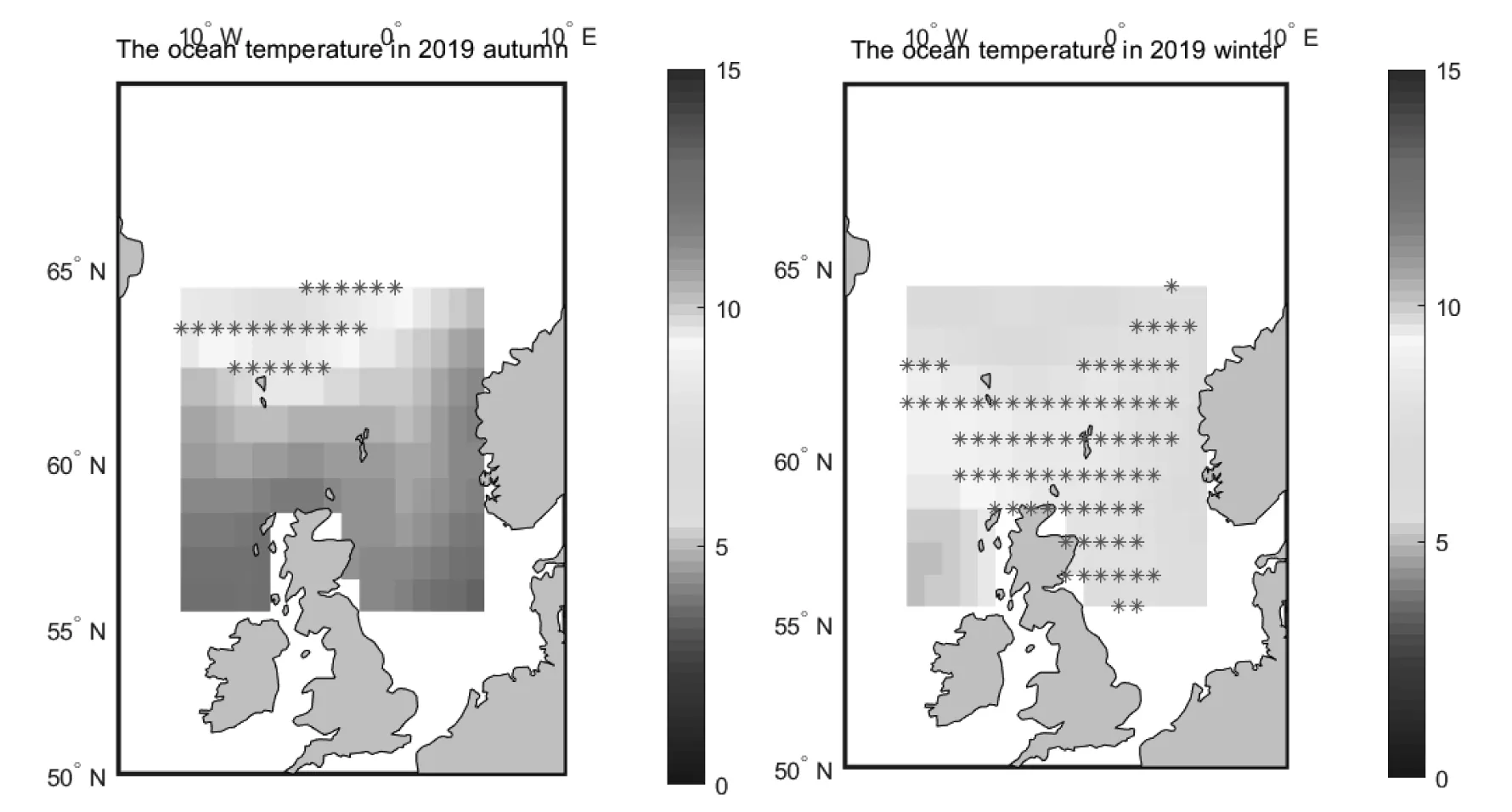
图2 2019年春夏秋冬4个季节水深200 m处的温度鱼群分布

由图2可知鱼群在春季和冬季分布较多，夏季和秋季分布较少.从捕鱼角度来看，选择鱼群分布多的季节，即春季和冬季，所以对春季和冬季的温度数据取平均进行作图.对于缺失数据应用双线性差值进行处理，查看1990年和2019年的鱼群分布情况，具体如图3所示.

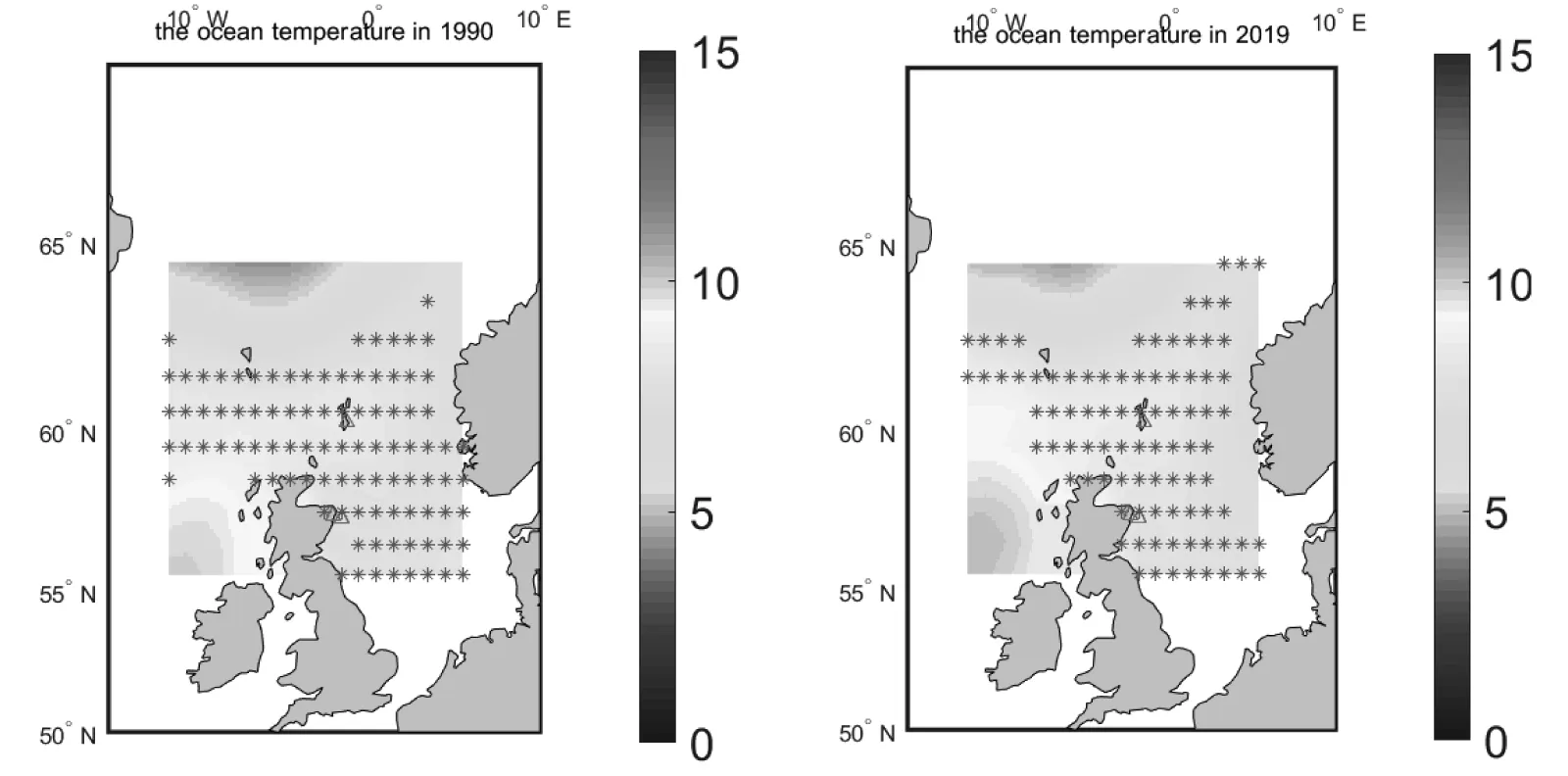
图3 1990年和2019年鱼群的栖息地可能位置(星号表示鱼群位置)

可以看到，1990～2019年的29年间温度有上升，相应鱼群位置会发生改变，有向北迁移趋势.

2 基于BP神经网络预测温度变化的模型

2.1 BP神经网络的建立

人工神经网络是20世纪80年代迅速发展起来的一门非线性科学，无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果[6].其中反向传播网络，即BP神经网络，是一种具有逼近非线性映射关系的神经网络.BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，其算法称为BP算法[7].它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小.

对于未来50年温度变化的预测采用BP神经网络，输入参数为年份和经纬度，输出参数为温度.基本原理可以表示为

F(Year,Lon,Lat) →T

(2)

式中：F表示输入参数与输出参数的映射关系，Year表示样本的年份，Lon与Lat分别表示样本的经度和纬度，T表示样本的温度值.

2.2 BP神经网络的设计

2.2.1 节点转移函数的选择

常见的节点转移函数[8]，主要包括以下3种.

(1)logsig函数：

(3)

(2)tansig函数：

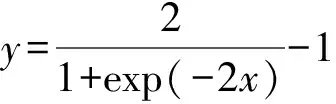
(4)

(3)purelin函数：

y=x

(5)

一般隐含节点转移函数选用logsig或tansig函数，输出层节点转移函数选用tansig或purelin函数.该文中隐含节点转移函数选用logsig函数，输出层节点转移函数选用purelin函数.

2.2.2 训练函数的选择

训练函数主要包括Levenberg-Marquardt、Bayesian Regularization(贝叶斯正则化方法)和Scaled Conjugate Gradient(尺度共轭梯度方法)3种训练函数.其中，Levenberg-Marquardt方法更适用于最小二乘曲线拟合，Bayesian Regularization用于分类，Scaled Conjugate Gradient是一种迭代算法.该文采用Levenberg-Marquardt算法进行训练，该算法比起传统的BP算法而言，其梯度下降要快很多，从而在整个网络上能以很少的迭代次数达到误差要求[9].

2.2.3 隐含层神经元数目的选择

在神经网络模型中神经元个数的选择是影响模型输出的重要因素.尽管神经元个数的增加可以使得模型能更快速的拟合，但同时也会带来模型的不稳定，导致使用非建模数据模拟时产生拟合度变差.

在设计隐含层时，根据经验公式[9]：

(6)

式(6)中h为隐含层神经元个数；n为输入层神经元数；m为输出层神经元数；a为1～10之间的常数.所以，初步确定隐含层神经元个数为3～12之间，为了找到最优的神经元个数，采用枚举法进行最优值的选取.

2.3 BP神经网络的训练

在数据集中选取了春冬季节的1990～2010年的数据建立神经网络，并用春冬季节的2010～2019年的数据作为检验.在进行BP神经网络训练前，为避免原始数据过大造成的网络麻痹，对原始数据进行归一化处理.

选择最大训练次数为500次，学习率为0.01，期望误差为10-5.用以上参数对所涉及的BP神经网络进行训练.

检验标准为模拟结果与实际结果的均方根差(not-mean-square error ,RMSE)和相关性系数R计算公式为式(7)与式(8).RMSE越小，R越接近1，则代表模型越接近实际映射[6].

(7)

(8)

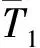
采用枚举法选取不同的神经元个数进行训练，由于每次训练结果不稳定，因此每选取一个神经元个数就对神经网络进行10次训练，每次可以得到相应的均方误差和相关系数，最后对10次均方误差和相关系数取平均可以得到如图4所示的模型比较.

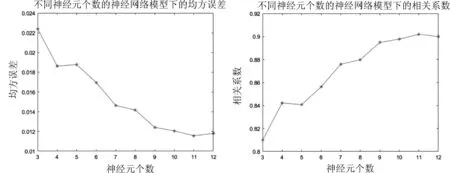
图4 不同隐含层神经元个数的神经网络模型比较

从图4可以看出随着神经元个数的增加，均方根差RMSE在逐渐降低，其相关性系数R也不断接近1.经过比较，神经元的个数为11时温度检验效果较好.

通过上述对神经元的选择，最终建立一个具有11个神经元的3层BP神经网络模型，输入神经元为3个(年份Year,经度Lon,纬度Lat)，输出神经元为1个(气温T).根据原数据进行训练和测试，可以得到效果较好的BP神经网络模型.

2.4 基于BP神经网络的温度预测

根据MATLAB对原数据进行训练和预测，建立BP神经网络模型依此得到未来50年的温度变化，可以得到部分变化数据见表1.可以看到，随着年份增加，温度呈上升趋势明显.进一步根据此数据作热力图进行可视化，图5描绘了2069年的鱼群位置分布.

表1 预测未来50年的部分温度变化数据

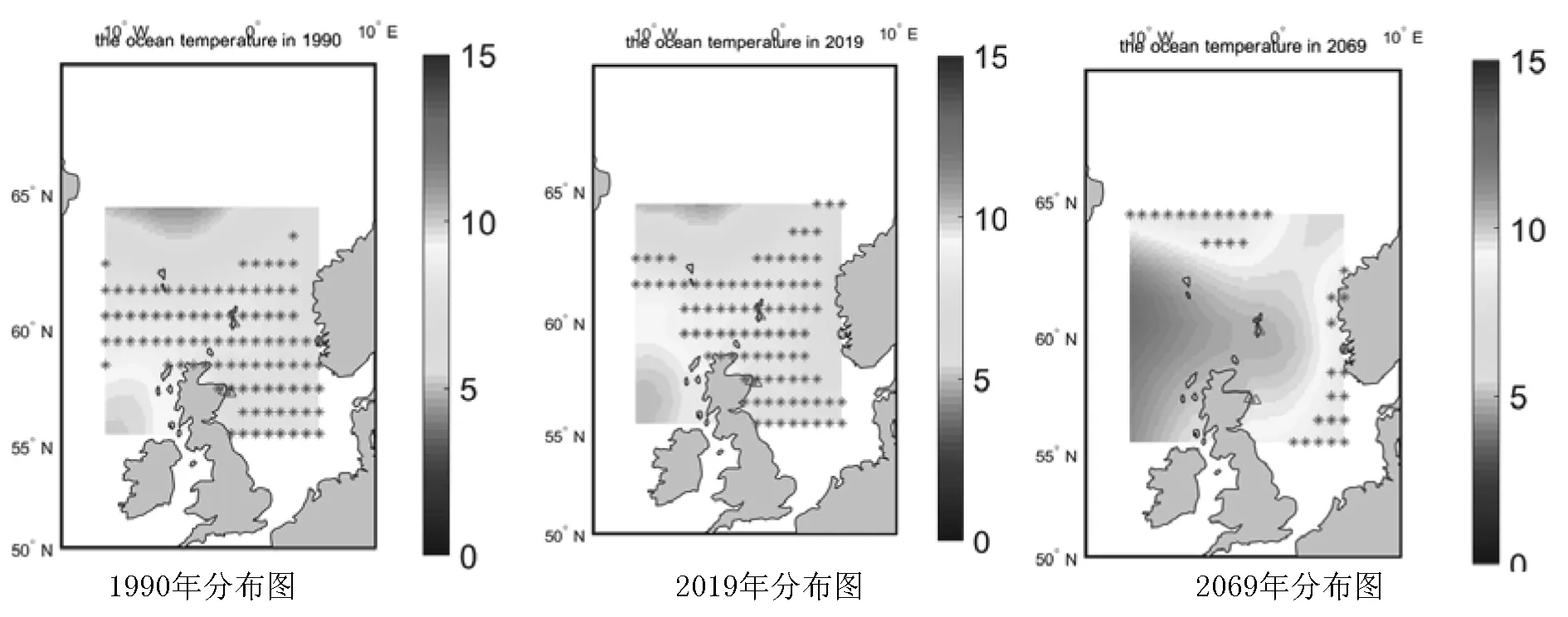
图5 鱼群位置对比图

由图5可以看出，鱼群位置在不断发生改变，50年后，鱼群整体向北、向东迁移.第50年时两种鱼类的可能分布区域为北纬55.5°到61.5°，东经3.5°到5.5°；北纬64.5°，西经168.5°到178.5°(55.5°N、61.5°N、3.5°E、5.5°E；64.5°N、-1.5°E、11.5°E ).

3 结 论

该文通过分析鲱鱼和鲭鱼两类鱼群在苏格兰海域所处的分布位置和温度范围，提出了建立BP神经网络对海水温度的变化进行预测，并由此获得鱼群迁移方向.文中用到的BP神经网络分析方法在多因素、多水平的实验条件下，能够获得更加全面和准确的试验结果.BP神经网络具有较强的非线性映射能力，实现了一个从输入到输出的映射功能，适合于求解该文探讨的这种内部机制复杂的问题.