压力容器环形下降段内含硼溶液流动混合特性的数值模拟分析

杜为安，张 琦，杨继行，闫超星，张 翼，刘成洋

(1.中国舰船研究设计中心，湖北 武汉 430061；2.上海交通大学 核科学与工程学院，上海 200240)

典型压水反应堆在一回路冷却剂内添加硼酸来补偿剩余反应性，硼酸溶液在反应堆压力容器以及一回路管道内的分布特性直接影响堆芯功率[1-3]。当堆芯供冷不足、堆芯内产生大量水蒸气时，由于硼酸在蒸汽中溶解度较小，几乎不含硼的水蒸气经过蒸汽发生器后将形成不含硼的冷凝液(称为稀释水团)。稀释水团将聚集在压力容器入口上游的相关管路中[4]，这部分稀释水团进入压力容器后将会和含硼冷却剂混合，并最终进入堆芯。堆芯应急冷却系统启动后，安全注射水箱中的高浓度硼溶液被注入压力容器内与一回路冷却剂混合后进入堆芯。安注冷却剂和一回路冷却剂之间还可能导致热分层[5-6]。上述含硼溶液的混合过程直接关系到堆芯反应性的变化，搅混不均匀可能导致堆芯反应性激增或功率分布偏移，进而威胁堆芯安全。

压力容器的环形下降段位于堆芯入口上游，研究含硼溶液在环形下降段内的混合过程对反应堆安全具有重要意义[1,7]。国内外已开展过含硼溶液混合相关的实验[2,8-9]，受测量技术限制，现阶段的相关实验只能获得环形下降段内局部位置的平均硼浓度分布。计算流体力学(CFD)软件成本较低、可重复性高，并可对三维场的流动与混合过程进行分析，被广泛应用于反应堆热工水力的相关研究。本文基于计算流体力学软件ANSYS Fluent 18.0对环形下降段内的流动与混合特性进行分析。

1 数值模型

1.1 控制方程

本文基于不可压缩流体假设，忽略温度变化对浓度扩散的影响，控制方程如下。

1) 连续方程

连续方程即质量守恒方程，其微分形式为：

(1)

式中：u、v、w为x、y、z方向速度分量，m/s；ρ为密度，kg/m3；t为时间，s。

2) 动量方程

动量方程实际上是牛顿第二定律，x、y、z方向的动量方程为：

(2)

(3)

(4)

式中：p为流体微元体上的压力，Pa；τxx、τxy、τxz等为黏性应力τ的分量，Pa；fx、fy、fz为x、y、z方向的单位质量力，m/s2，若质量力只有重力，z轴竖直向上，则fx=fy=0，fz=-g。

3) 能量方程

包含有热交换的系统必须满足能量守恒定律，其本质为热力学第一定律，表达式为：

(5)

式中：E为流体微团总焓值，J/kg，由内能、势能和动能组成，E=h-p/ρ+u2/2；hj为组分j的焓值，J/kg；Jj为组分j的扩散通量；k为流体热传导系数，W/(m·K)；Sh为包括化学反应及其他体积热源项。

4) 组分质量守恒方程

在存在质的交换或多种化学组分的特性控制系统中，每一组分都要遵循组分质量守恒定律。对于一特定的系统，组分质量守恒定律可描述为：系统内某组分对时间的变化率等于通过系统界面的净扩散流量和化学反应生成率之和。

由组分守恒定律，得到组分s的组分质量守恒方程:

(6)

式中：cs、ρcs为组分s的体积浓度和质量浓度；Ds为组分s的扩散系数；Ss为源项。式(6)从左到右分别为时间变化率、对流项、扩散项和源项。

1.2 模型建立与网格划分

本文参照哈尔滨工程大学激光诊断实验室的硼浓度混合分析实验[10]建立相应的物理模型，以便于对比实验结果与数值模拟结果。表1为压力容器物理模型的相关参数。图1为压力容器物性模型的俯视图和正视图。流体经入口管进入环形下降段，流入下腔室后从下腔室上部的7×7矩形通道流出。下腔室并不是本文关注的重点，在保证流体流动方向不变的情况下，简化下腔室内构建，仅保留半球形结构和上部孔板。

表1 压力容器模型参数Table 1 Parameter of reactor model

图1 压力容器简化模型Fig.1 Mock RPV model

采用ANSYS ICEM对模型进行网格划分，网格结构如图2所示。将压力容器模型分为入口管段、环形下降段、下腔室和矩形出口通道4个主要区域，各区域均采用六面体结构化网格，各区域交接面的节点一一对应。经无关性验证后(图3)，最终网格数量约为127万，网格质量为0.55。

1.3 湍流模型

Rohde等[11]结合硼混合实验数据进行湍流模型验证，并指出不考虑浮升力影响的情况下，SST模型可准确计算压力容器内硼浓度分布。SST模型对壁面附近的低雷诺数流动区域采用标准k-ω模型，对充分发展的自由流动区域采用标准k-ε模型，因此很大程度上降低了标准k-ω模型对自由剪切流的敏感程度[12-13]。SST模型的输运方程如下：

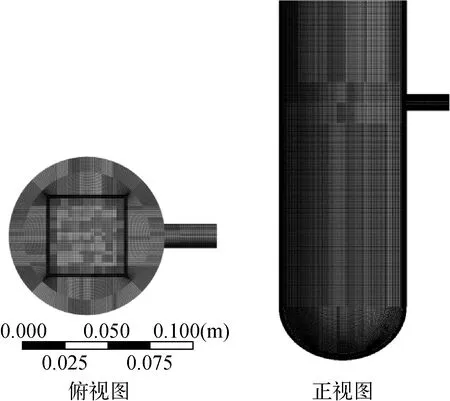
图2 压力容器模型网格划分Fig.2 Meshing of RPV model

图3 网格无关性验证Fig.3 Independence validation of mesh number

(7)

式中：Gk为由时均速度梯度引起的湍流动能产生项；Gω为湍流涡频率产生项；Yk和Yω分别为湍流动能及湍流涡频率的耗散项；Dω为交叉扩散项。

为验证CFD计算结果的准确性，将数值模拟和实验得到的入口横截面平均质量分数进行对比，结果如图4所示。可看出，入口横截面的平均质量分数随注射时间的增加而增大，在10 s后增长速度明显减缓。CFD计算结果与实验结果较为一致，平均相对误差为3.41%。说明本文计算结果具有较高的准确性。

图4 数值模拟结果与实验对比Fig.4 Comparison between CFD simulation and experiment

1.4 边界条件设置

开启混合物模块，自定义硼酸溶液和水溶液的混合物，通过编写UDF设置二者的组分占比，入口流速分别设置为0.2、0.3、0.4 m/s，硼酸质量分数c设置为：t≤0 s时，c=0；t>0 s时，c=0.1。系统运行压力为0.1 MPa，混合物的物性设置为常压下水的物性。忽略硼示踪剂对流体的物性影响，流体密度为998.2 kg/m3，运动黏度为0.001 Pa·s。入口边界条件设置为速度入口，出口边界条件设置为压力出口，壁面类型选择无滑移壁面边界条件。模拟混合过程前首先将压力容器内的全部流体定义为水，t>0 s时含水混合物自入口注入压力容器。

2 数值模拟结果与分析

2.1 环形下降段内流动特性分析

1) 二维速度场分析

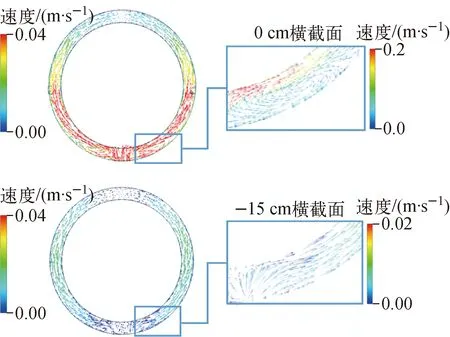
图5 水平方向速度矢量分布Fig.5 Transverse velocity vector

图5为横截面的速度矢量分布，对应的入口雷诺数为11 448。可看出，在0 cm横截面周向位置[10°，30°]和[-30°，-10°]区域存在较大尺度的涡结构，由于入口流体与内壁发生剧烈碰撞，流体呈放射状散开，在靠近入口管道的区域形成回流并与环腔内流体混合。Eltayeb等[14]通过可视化实验在该区域观测到了旋涡的形成与瓦解过程，旋涡的尺寸与位置存在一定的随机性。而数值模拟结果仅能观测到1个尺度较大的涡，这是由于两方程涡黏模型基于平均化假设，在瞬态条件下无法计算出脉动值[15]。在单回路流动实验的初始阶段(0～2 s)，示踪剂在上述区域的扩散过程与速度矢量分布相对应，染色剂与内壁发生碰撞后形成逆流向外壁发展。随后流体沿环形区域周向位置流动，期间不断与环腔壁面发生碰撞，水平方向的速度随周向位置的延伸而衰减，在[90°，130°]和[-130°，-90°]的区域最为明显。在水平位置较低的-15 cm横截面，[45°，135°]和[-45°，-135°]区域的流体流动不受上游涡结构的影响，速度分布较为平稳。

图6、7分别为环形下降段内水平方向和竖直方向的速度分布。如前文所述，流体进入环腔后沿周向位置扩散，期间不断与壁面发生碰撞，水平方向动能不断损失，水平方向的速度随周向位置的增加而衰减。注意到-10～-25 cm截面水平方向速度先增加后减小，其中以图6a最为明显，这是由于靠近入口管道的区域受放射状回流的影响。部分入口流体与内壁碰撞后将沿竖直方向进入环腔下部空间；环腔上部空间的入口流体受质量力影响也会逐渐沿竖直方向沉降，可看出水平位置越低的截面，竖直方向的速度分量越大。

2) 三维流线图分析

图8为单回路稳态流动条件下环形下降段和下腔室内的流线图。流体经入口管进入压力容器后与环腔内壁发生剧烈碰撞并形成回流，部分回流受边界条件的束缚沿内壁呈放射状散开。随后入口流体分成两股沿着环形下降段周向位置流动，竖直方向的速度分量随周向位置的延伸而增加，到达入口对侧后环腔左右两股流体开始汇合。

图6 水平方向速度分布Fig.6 Transverse velocity distribution

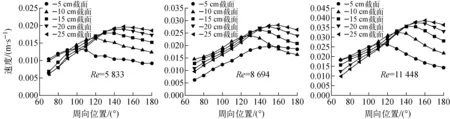
图7 竖直方向速度分布Fig.7 Longitudinal velocity distribution

图8 环腔与下腔室内流线图Fig.8 Streamlines in down-comer and lower plenum

流线图可反映微元流动介质在流场中的轨迹。从图8可看出，在入口正下方和环腔上部空间存在流动停滞区，该区域随入口雷诺数的增加而收缩。在主泵恢复工作的工况下，主泵转速由控制器驱动呈点动式增加而非线性增加，持续的低速转动可能导致稀释水团滞留在环腔上部空间，与冷却剂交混过程缓慢。

2.2 硼输运特性分析

1) 橫向浓度场分布

将数值模拟得到的横截面混合物质量分数分布与文献[10]所报道的示踪剂浓度分布进行比较，结果如图9、10所示。从数值模拟结果可看出，混合流体进入环腔后与内壁发生碰撞，随后沿着周向位置发展并不断与环腔内流体混合；周向位置越大，混合物扩散的速度越慢。在图9、10中，数值模拟图像中的比色卡为混合物份额，而实验结果图像的比色卡为染色剂(RhB)的浓度，二者的扩散趋势高度一致，进一步验证了模型的可靠性。SST模型能得到浓度扩散整体趋势，但无法获得湍流扩散的细节。在数值模拟结果中可观测到入口位置内壁和外壁之间存在一定的浓度梯度，而实验结果显示该区域的混合较为充分，浓度梯度较小。

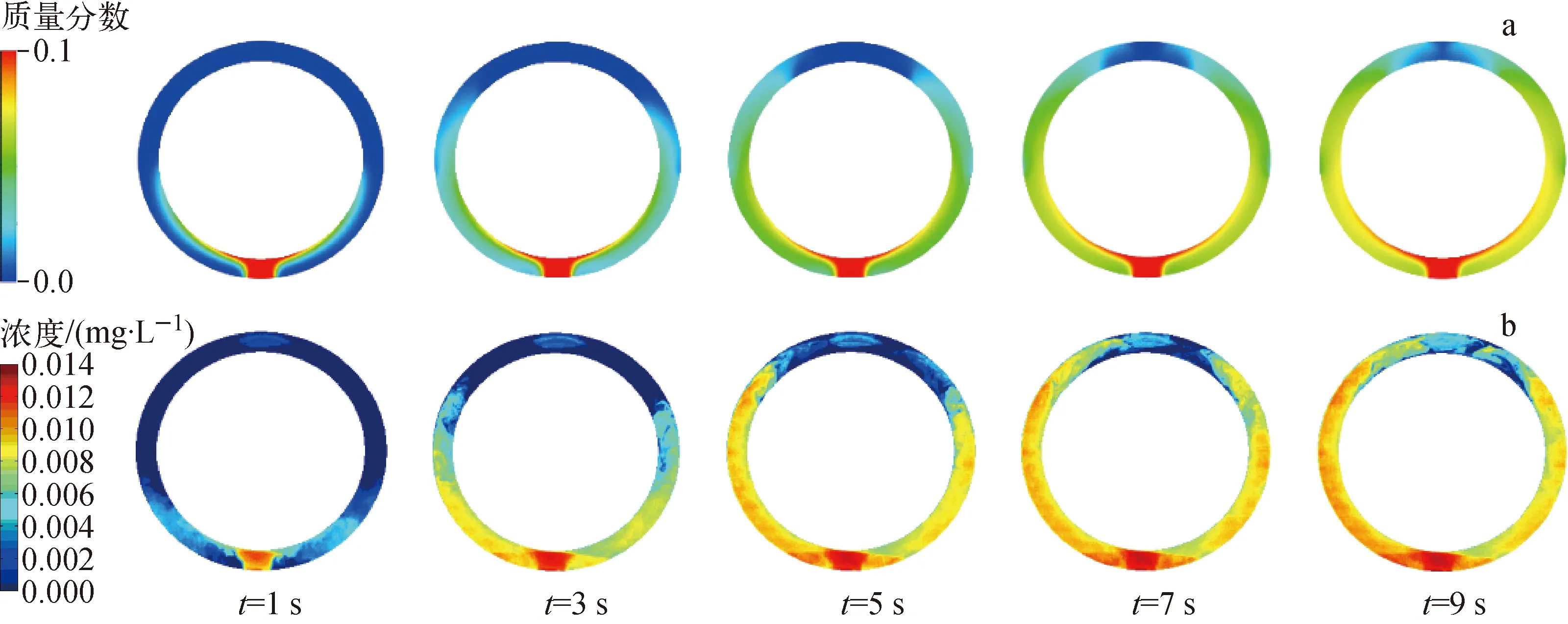
a——数值模拟质量分数分布；b——LIF实验染色剂浓度分布图9 0 cm横截面实验与数值模拟结果对比Fig.9 Contrast between numerical simulation and experimental results at 0 cm cross section

a——数值模拟质量分数分布；b——LIF实验染色剂浓度分布图10 -10 cm横截面实验与数值模拟结果对比Fig.10 Contrast between numerical simulation and experimental results at -10 cm cross section

图11为周向位置质量分数数值模拟与浓度实验结果。从图11a可观测到，混合物进入环腔后在入口位置持续出现1个质量分数的峰值，由于入口流体在水平方向通过的距离较短，且尚未与环形下降段内外壁发生碰撞，混合特性较差。随后高浓度硼溶液沿周向位置流动并不断与水发生混合，环腔内混合物所占区域不断增加，如图11b所示。可注意到，在t>5 s后，周向角为[30°，110°]和[-30°，-110°]区域的质量分数平稳增长，说明该区域的混合物已与水充分混合。从图11可看出，周向位置质量分数不断展平，质量分布区域均匀。由于压力容器模型加工精度所限环腔两侧浓度分布轻微不对称，整体上，数值模拟结果与实验结果较为一致，实际流动过程染色剂发展的边缘位置存在一定脉动。

2) 三维浓度场分布

图12为硼酸溶液注入环形下降段后的质量分数分布。含硼溶液进入压力容器后呈放射状散开，并绕环腔壁边界流动；混合物到达周向位置较大的区域后水平方向的速度衰减，其输运特性过渡为沿竖直方向的沉降，以图12b中t=24 s时刻最为明显。从图12可看出，单回路流动混合时，入口正下方存在1个流动停滞区，在整个混合过程中模拟硼酸溶液无法进入到流动停滞区。可见，同等时间下，入口混合流体雷诺数越大，混合物所分布的区域相应越大，整个环腔内的流通停滞区相应收缩。文献[10]所报道的示踪剂浓度扩散特性与该现象一致。

a——周向位置质量分数分布数值模拟；b——周向位置浓度分布LIF实验结果图11 数值模拟与实验结果定量对比Fig.11 Quantitative contrast between numerical simulation and experimental results

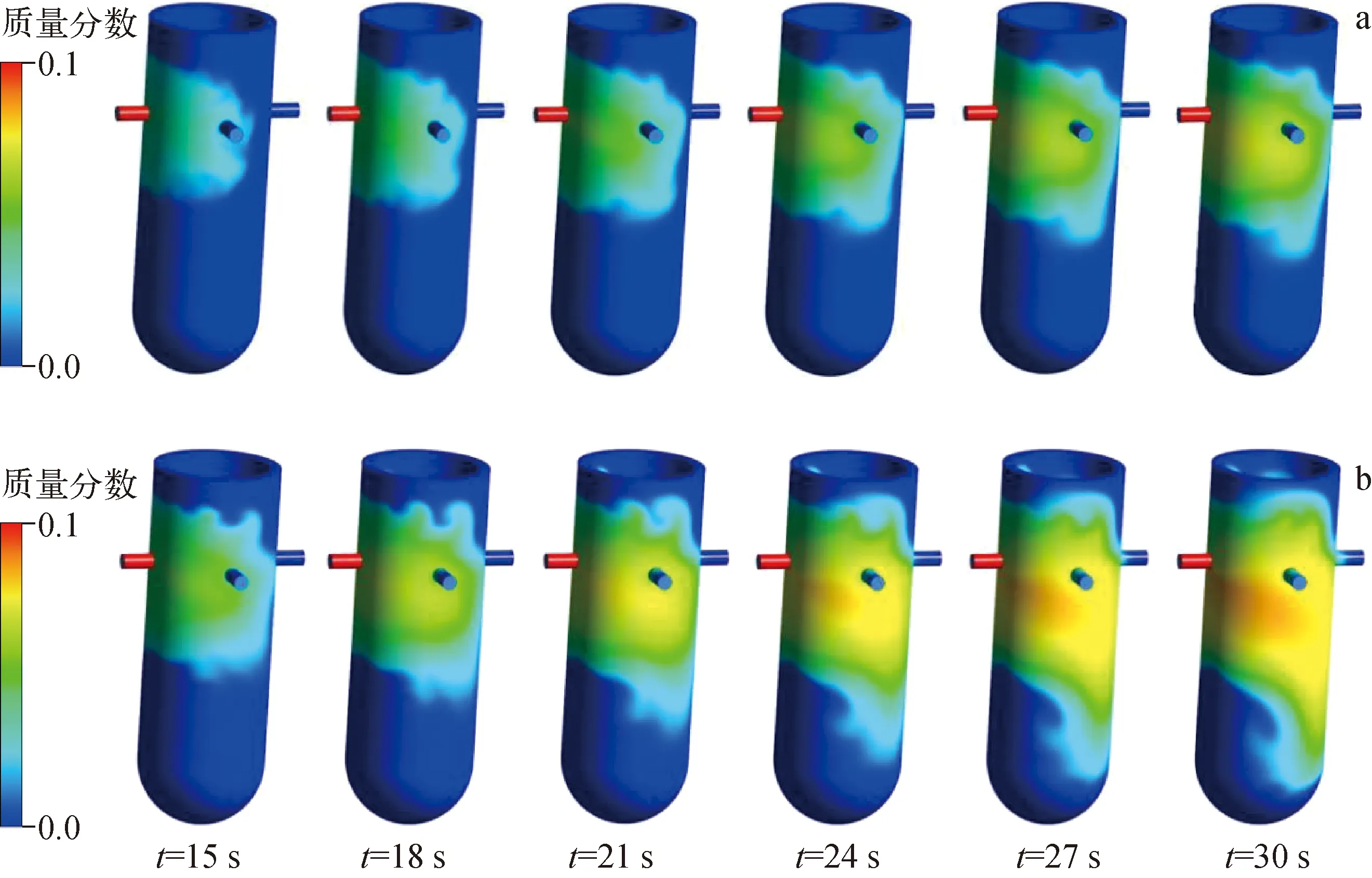
a——Re=5 833；b——Re=11 448图12 压力容器三维质量分数分布Fig.12 Three-dimensional mass fraction distribution in RPV

3 结论

本文基于SST模型对环形下降段内的硼混合问题进行了分析，得到如下结论。

1) 单回路条件下，环形下降段上部空间水平方向的速度梯度较大，下部空间流体流动较为稳定；环形下降段内存在流动停滞区，且该区域随入口雷诺数的增加而收缩。

2) 含硼溶液从单一入口进入压力容器后将沿环形下降段周向输运，期间水平方向动能不断损失，在环腔内的输运特性逐渐过渡为沿竖直方向的沉降。