基于最佳一致逼近多项式的燃耗计算方法研究

张彬航，张 聪，毕彦钊，张永红，袁显宝，唐海波，冯虹瑛

(三峡大学 机械与动力学院，湖北 宜昌 443002)

反应堆燃耗计算是反应堆设计与分析的重要环节[1]。在实际计算中，其核心是求解燃耗方程，并通常假设反应率在单个时间步长内恒定，因此燃耗方程可被视为一阶线性方程组。其矩阵方程和指数解的形式如下：

(1)

(2)

式中：N(t)∈Rn为t时刻的核素密度向量；A∈Rn×n为燃耗系数矩阵，由系统中所有核素的反应率和衰变率组成。

由于堆内核素繁多，且不同核素的衰变常量数量级跨度极大，使得燃耗方程组具有大型、稀疏、刚性的特性，常规解法无法精确计算此问题。为精确计算矩阵指数eAt，近年来诸多基于近似理论和矩阵理论的计算方法得到了广泛的发展与应用，如切比雪夫有理近似方法(CRAM)和围道积分有理近似方法(QRAM)[2-3]。CRAM基于复平面将指数函数的最优有理近似式扩展到矩阵指数上以逼近eAt：

(3)

QRAM则是基于柯西积分公式和围道求积组将式(2)转换为复平面上的积分表达式：

(4)

式中：C为包围矩阵At所有本征值的闭合围道；zk为求积组的插值点；ck为相应插值点的权重；N为展开阶数。点燃耗程序MODEC采用32阶QRAM和优化后的抛物线围道求积组用于燃耗计算中，取得了较好的计算精度和效率[5]。

由式(3)、(4)可发现，为求解t时刻的核素密度，CRAM和QRAM需分别进行k/2和N次大规模稀疏矩阵的求逆计算，且所有计算皆为复数运算，计算效率有限。

本文研究一种基于最佳一致逼近多项式(MMPA)的燃耗计算方法，只需进行1次矩阵求逆计算即可求解燃耗方程，具有较高的计算效率。并研制点燃耗程序AMAC，与蒙特卡罗输运程序OpenMC进行耦合，通过计算衰变和固定辐照例题、OECD/NEA压水堆栅元燃耗基准题和沸水堆组件燃耗基准题初步验证该方法的正确性和有效性。

1 最佳一致逼近多项式方法

基于近似理论和矩阵理论[6]，矩阵指数eAt可由某一确定矩阵函数f(At)进行逼近。若设矩阵At的特征值为{λ1,λ2，…，λn}∈C,则矩阵At可通过非奇异矩阵P转换为Jordan标准型：

(5)

式中：J(λi)为对应矩阵特征值λi的Jordan块；矩阵P和P-1对应于每个Jordan块J(λi)，可转换为：

(6)

对于矩阵At的特征值{λ1，λ2，…，λn}，若可为每个特征值λi定义函数f(λi)及其到ki-1阶的导数fki-1(λi)，则矩阵函数f(At)的一般表达式[7]为：

(7)

式中：ki为最大Jordan块J(λi)的大小；n为矩阵At的特征值个数；Gi为(At-λiI)j在其广义本征空间上的投射矩阵。由式(7)可得被逼近矩阵指数eAt的一般表达式[7]为：

(8)

由式(7)、(8)可知，对于矩阵At的每个特征值λi，若函数f(λi)及其导数f(j)(λi)在逼近指数eλi时有足够小的误差，则矩阵指数eAt可由矩阵函数f(At)进行最佳近似。根据文献[8]可知，燃耗矩阵At的本征值{λ1，λ2，…，λn}位于复平面上的负实轴附近。因此，在矩阵函数f(At)对矩阵指数eAt进行最佳逼近时，应满足如下两个条件：1) |f(At)-eAt|在负实轴附近足够小；2) |f(j)(λi)-eλi|/j!在负实轴附近足够小。为求出满足上述条件的函数f(At)，本文基于MMPA对矩阵指数eAt进行了最佳近似，定义多项式函数f(t)为：

(9)

式中：a0、ai∈R为多项式系数；n为展开阶数。

(10)

则通过变量代换后可得到指数函数ex的近似表达式：

(11)

式中，x∈(-∞,0]。根据文献[9]可知，当常数c取24.1并进行32阶展开时，最大近似误差的最小值为2.2×10-14，能满足燃耗计算的高精度要求。基于Remez算法[10]可得32阶MMPA方法的实数系数ai。由于系数ai皆为实数，因此在进行燃耗计算时不需进行复矩阵运算，这是MMPA方法相对于CRAM、QRAM等有理近似方法的优点之一。由式(2)和(11)可得t时刻的核素密度N(t)为：

(At-cI)-1}iN(0)

(12)

式(12)中，矩阵(At+cI)(At-cI)-1的特征值λ′i为：

(13)

由于矩阵At的特征值{λ1,λ2，…，λn}∈(-∞,0]，因此特征值λ′i∈[-1,1)，则在进行多项式逼近过程中{(At+cI)(At-cI)-1}i的特征值始终在区间[-1，1]上，具有良好的数值稳定性。如式(12)所示，为了求得t时刻的核素密度，只需获得矩阵(At+cI)(At-cI)-1后再进行31次迭代相乘即可。相对于目前广泛应用于燃耗计算的16阶CRAM和32阶QRAM分别所需的8次和32次复矩阵求逆相比，MMPA方法只需进行1次矩阵的求逆运算，在计算效率与方法实现上具有一定的优势。因此，本文进一步基于32阶MMPA方法开发了点燃耗程序AMAC，并耦合蒙特卡罗输运程序OpenMC以验证该方法的正确性和有效性。

2 程序开发

AMAC采用了精细燃耗数据库进行燃耗计算。该燃耗数据库整合了ORIGEN-2与ORIGEN-S的最新燃耗数据库，共包含1 487种不重复核素、11种衰变反应、23种中子截面反应和30种重核裂变产额数据[11-12]。同时AMAC也能直接读取ORIGEN-2或ORIGEN-S的燃耗数据库进行燃耗计算。在基于MMPA方法求解燃耗方程的过程中，由式(12)可知只需对矩阵(At-cI)进行1次求逆运算，考虑到该矩阵具有大型、稀疏、刚性的特性，直接采用高斯消元法会引入较大的舍入误差。为保证求解的精度和效率，AMAC首先对该矩阵进行符号LU分解，获得相应的填入矩阵，然后对填入矩阵进行高斯消元，从而完成矩阵(At-cI)的求逆[13]。另外考虑到矩阵的稀疏性，为节省内存及计算时间，AMAC采用三元组方法对稀疏矩阵进行压缩储存。

AMAC的简要程序架构如图1所示。程序主要分为前处理、求解器及后处理3部分。前处理部分主要读取燃耗计算中所需的数据，包括衰变常量、微观截面、裂变产额、通量、时间步长等信息，并将这些数据处理成燃耗矩阵的形式并存储，由求解器直接调用计算。求解器部分主要是根据不同的计算方法进行燃耗方程的求解。除32阶MMPA方法外，AMAC还实现了16阶CRAM和32阶QRAM的燃耗计算方法。后处理部分将计算结果进行格式化输出，输出数据包括核素密度、放射性活度、衰变热等。在完成点燃耗程序AMAC研制的基础上，进一步基于Python完成了与OpenMC的耦合以便计算真实的燃耗问题，并引入预估-校正和子步法两种耦合策略以保证燃耗计算的精度与效率。

图1 AMAC程序框架简图Fig.1 Brief structure of AMAC code

3 数值验证与分析

对于MMPA方法的正确性与有效性的验证，主要基于AMAC来完成，主要分为两个方面：一是在相同数据库下，计算了237Np的衰变和UO2燃料的固定辐照问题，并与ORIGEN-2和RMC程序进行对比，以验证MMPA方法在求解燃耗方程时的精度与效率；二是通过耦合程序OpenMC-AMAC完成OECD/NEA压水堆栅元燃耗基准题和沸水堆组件燃耗基准题的计算与验证分析，以评估MMPA方法计算实际燃耗问题的能力。

3.1 237Np的衰变计算

衰变例题计算了初始含量为1 mol的237Np衰变106a后各核素成分的变化。参考程序选取了ORIGEN-2和RMC，皆基于ORIGEN-2的燃耗库完成计算，计算结果和相对偏差列于表1。以RMC的线性子链解析方法的计算结果作为基准解，分别列出了ORIGEN-2和AMAC相对于基准解的相对偏差，可看到MMPA方法的计算结果沿燃耗链长度方向的相对偏差没有增大趋势，且与基准解吻合良好，最大相对偏差仅为0.03%。对于ORIGEN-2的计算结果，由于时间步长为1.0×106a，根据ORIGEN-2的处理机制，当核素半衰期小于燃耗时间步长的1/10时，就判定该核素为短寿命核素，需从燃耗矩阵中移除后进行平衡性假设处理，而燃耗矩阵中仅保留长寿命核素，以解决燃耗矩阵的刚性问题。在该例题中，沿燃耗链上的核素233Pa、225Ra、225Ac、221Fr、217At、213Bi、213Po、209TI、209Pb被判定为短寿命核素且需进行平衡性假设处理，导致这些核素“过度”衰变，使得这些核素的计算结果小于解析方法的计算结果，并最终使得燃耗链末端核素209Bi的计算结果大于解析解。MMPA方法计算时直接对燃耗矩阵At进行处理，不需单独处理短寿命核素，因此燃耗链长度的增长不会导致计算精度的明显下降。同时基于Remez算法求解多项式系数时严格遵守了对矩阵指数eAt进行最佳近似的两个约束条件，能保证求解精度。因此，MMPA方法对于长燃耗链的计算具有良好的精度和稳定性。在计算效率方面，ORIGEN-2耗时0.002 s，而MMPA方法的耗时仅为0.001 s。

3.2 UO2燃料的固定辐照计算

固定辐照例题计算了初始含量为1 mol、富集度为5%的UO2燃料，在3.0×1014cm-2·s-1的中子注量率下辐照1 a再冷却3 a后的各核素成分变化情况。辐照时间和冷却时间各划分10个子步长，参考程序选取RMC，使用其点燃耗计算功能完成了该例题的计算[14]。表2列出重要锕系核素和部分代表性核素的计算结果。与RMC所采用的16阶CRAM的计算结果相比，AMAC所采用MMPA方法的计算结果与其最大相对偏差不超过0.02%，具有较高的数值精度和稳定性。在计算效率方面，AMAC还使用了16阶CRAM与32阶QRAM对该例题进行了测试，在保留4位有效数字的情况下，这两种计算方法的结果与32阶MMPA方法完全一致。各方法的计算时间列于表3，可看到MMPA方法相对于其他方法在计算效率上有一定的优势。

表1 237Np衰变链的计算结果Table 1 Calculation result of 237Np decay chain

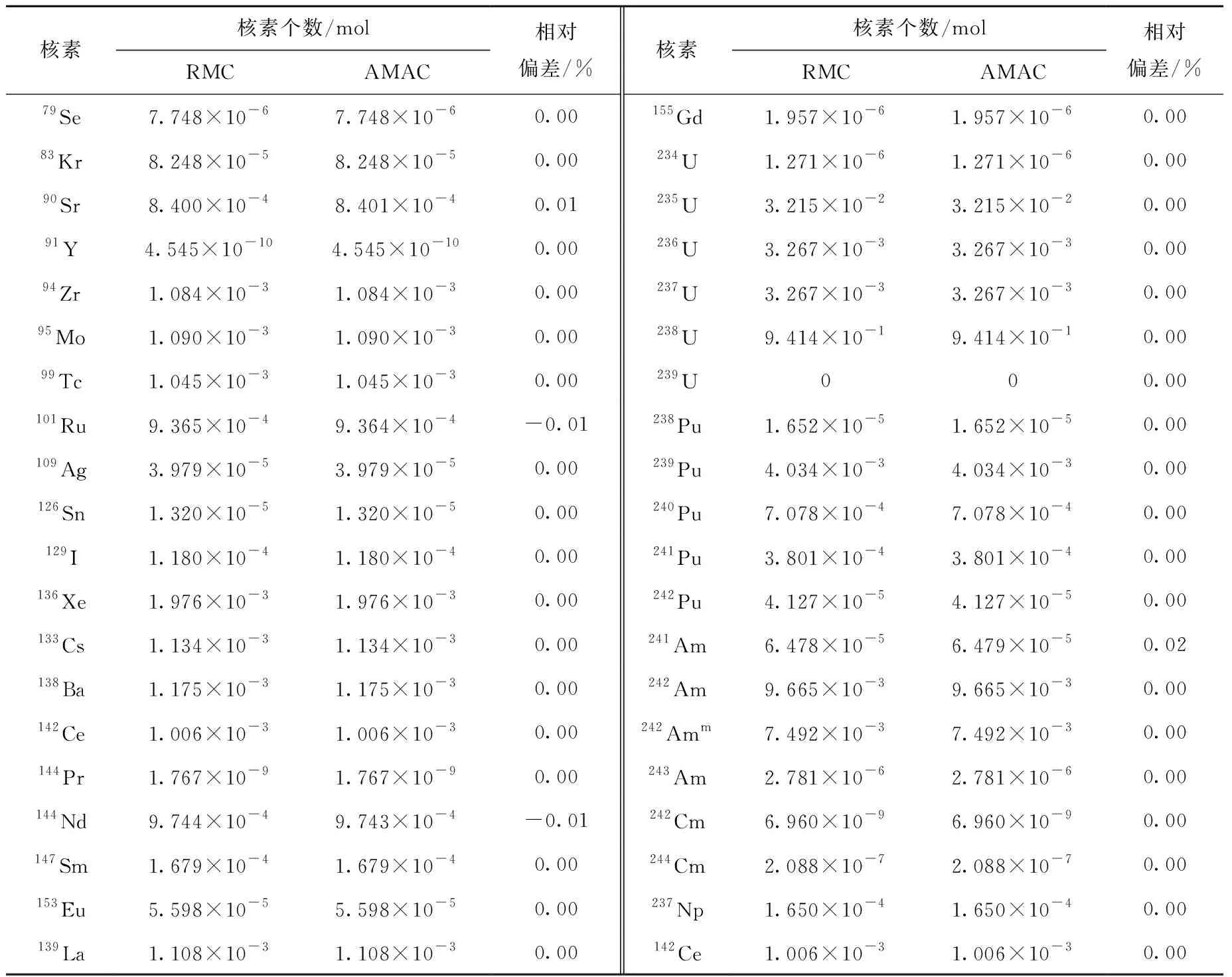
表2 5% UO2燃料的计算结果Table 2 Calculation result of 5% UO2 fuel

表3 不同计算方法的计算时间Table 3 Computing time of different methods

3.3 OECD/NEA压水堆栅元燃耗基准题

该基准题的计算目标是通过计算压水堆组件中的单个栅元以比较不同程序对燃料中同位素成分的计算与分析能力。根据功率和最终燃耗深度的不同，该基准题包括工况A(27.35 GW·d/tHM)、工况B(37.12 GW·d/tHM)和工况C(44.34 GW·d/tHM)，详细几何与材料参数参考文献[15]。

耦合程序OpenMC-AMAC采用MMPA方法和ORIGEN-2燃耗数据库完成了工况C的计算。同时基于数据库ENDF/B-Ⅶ，Serpent程序采用16阶CRAM也完成了计算[16]，计算结果列于表4。由表4可见，OpenMC-AMAC计算得到的大部分核素质量结果与实验值的相对偏差在5%以内，表明MMPA方法具有良好的数值精度和稳定性。其中对于裂变产额的计算，除核素149Sm外，其余核素的计算结果均在合理范围之内。149Sm的相对偏差为-26.493 6%，可能是149Sm的产生量太少或消失量太多所导致。149Sm从其先驱核149Nd经过两次β-衰变而来，而其消失途径主要为(n，γ)反应，所以ORIGEN-2的衰变数据和裂变产额会影响149Sm的产生量，OpenMC给出的(n，γ)截面会影响149Sm的消失量。因此，OpenMC计算的截面数据或ORIGEN-2的衰变数据的准确度会导致149Sm产生较大偏差。进一步发现Serpent的计算结果与AMAC吻合较好，但同样与测量值相差很大，因此该基准题的149Sm测量值可能存在问题[17]。对于锕系核素的计算，238Pu的相对偏差相对于其他一些锕系核素较大，为-4.828 9%。在燃耗计算中，238Pu、237Np这些核素主要由其他核素衰变产生，衰变库的数据准确度直接决定了这些核素的计算精度。同时OpenMC的统计误差也会影响核素的最终计算精度。为精确比较不同燃耗计算方法的耗时情况，统计了OpenMC-AMAC与Serpnet仅在进行燃耗计算时的耗时情况，其中AMAC耗时26.45 s，Serpent耗时26.41 s，两者效率相当。

3.4 OECD/NEA沸水堆组件燃耗基准题

该基准题由OECD/NEA发布，旨在比较不同燃耗程序在计算含可燃毒物组件时的能力。该沸水堆组件采用了8×8的排列方式进行燃料棒布置，其中包含8根含钆燃料棒以吸收寿期初的剩余反应性。总的燃耗深度为40 MW·d/kgHM，功率密度为25.6 W/gHM，详细的几何与材料参数参考文献[18]。

表5列出核素密度的16套参考程序的计算结果、平均参考值和OpenMC-AMAC的计算结果。由表5可看出，本文计算结果均在参考值范围内，且大部分核素的计算结果与平均参考值的相对偏差在5%以内。对于相对偏差较大的核素，如243Am及Gd同位素，由于缺乏实验值和各程序所采用的数据库、输运方法及燃耗计算方法的不同，难以评价其计算结果的精确性。尤其对于Gd同位素，由于其中子吸收截面很大，对于燃耗步长、可燃毒物棒的径向划分等因素十分敏感。为进一步验证MMPA方法的正确性和稳定性，在燃耗步长相同的情况下，对8根含钆燃料棒进行了径向分区和计算，表6列出径向均分为3区、5区、7区、10区4种情况下Gd同位素的相对偏差。由表6可见，随径向分区数目的增加，Gd同位素的相对偏差显著下降。由于Gd同位素的吸收截面很大，这一特性将引起燃耗过程中中子注量率分布在短时间内的显著变化，因此进行合理的径向分区能有效提高钆棒的计算精度，得到合理的燃耗计算结果。

表4 工况C下OpenMC-AMAC核素质量的计算结果Table 4 Calculation result of OpenMC-AMAC under condition C

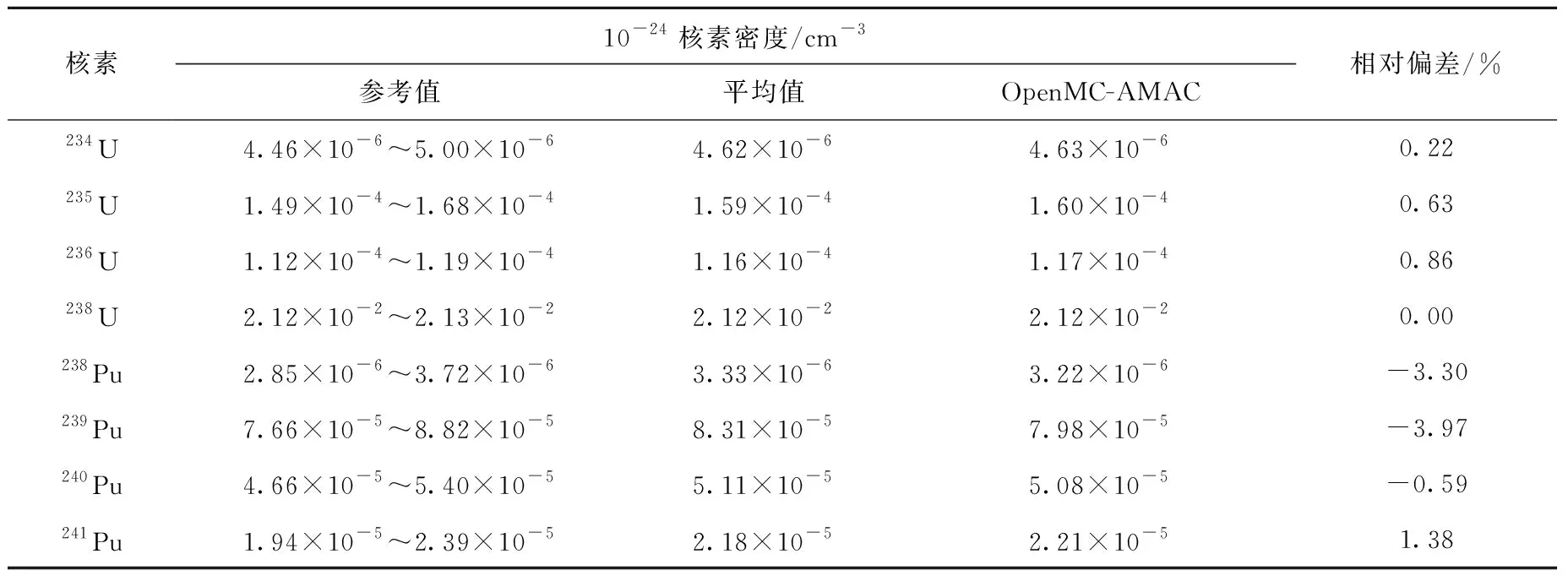
表5 OpenMC-AMAC核素密度的计算结果Table 5 Calculation result of nuclear density of OpenMC-AMAC

续表5

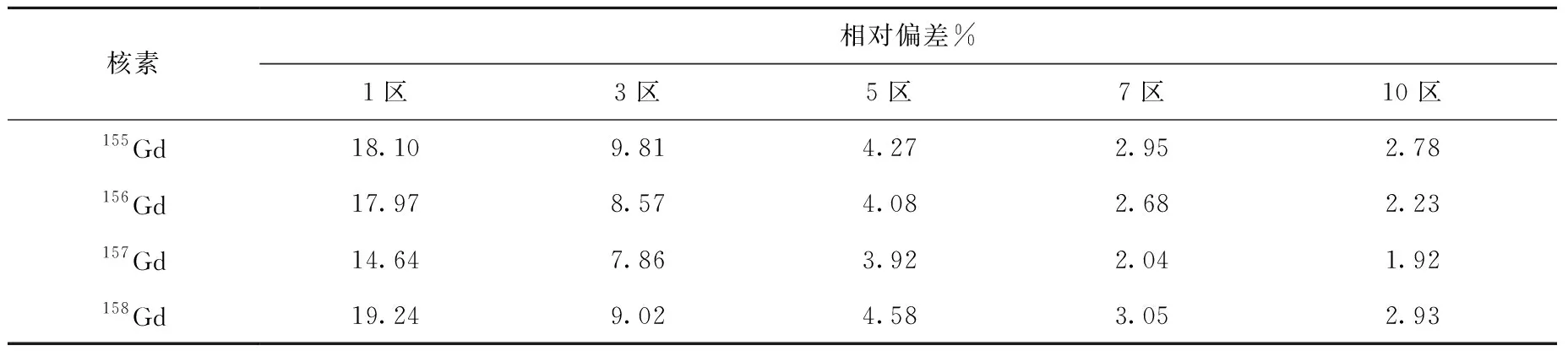
表6 不同径向分区下OpenMC-AMAC计算核素Gd的相对偏差Table 6 Relative deviation of Gd calculated by OpenMC-AMAC in different radial zones

表7列出组件的无限增殖因数k∞的计算结果，包括参考值、平均参考值、Serpent和OpenMC-AMAC随燃耗深度变化的计算结果。由表7可见，MMPA方法得到的k∞在参考值的区间内，且随燃耗深度变化的趋势相同，并与平均值的相对偏差较小。在燃耗计算效率方面，OpenMC-AMAC的燃耗计算耗时为1 664 s，Serpent耗时为1 710 s。总体来看，MMPA方法在进行燃耗计算时具有良好的计算精度与效率。

3.5 计算效率分析

通过上述基准题的验证与分析，可看到MMPA方法在燃耗计算中具有良好的计算精度和数值稳定性。在计算效率方面，对于32阶MMPA方法，由式(12)可知，为了求得t时刻的核素密度，只需获得矩阵(At+cI)(At-cI)-1后再进行31次矩阵的迭代相乘和相加。对于16阶CRAM方法，由式(3)可知，需对复矩阵进行8次求逆和7次相加即可求得t时刻的核素密度。理论上大型稀疏矩阵的1次求逆计算耗时高于矩阵的1次相乘或相加计算，因此MMPA方法的耗时应比CRAM方法少，这一点通过上述例题的耗时分析得到了验证，只是时间上的缩短效果有限。

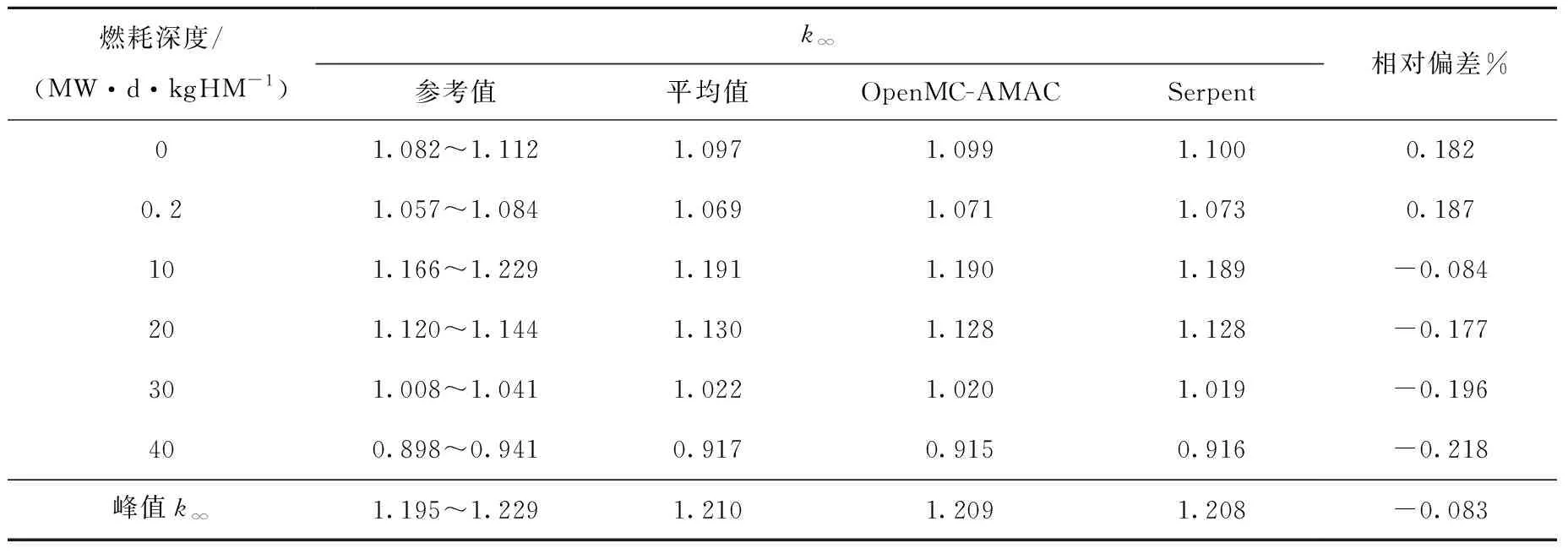
表7 OpenMC-AMAC的k∞计算结果Table 7 k∞ calculation result of OpenMC-AMAC

为了分析实际计算效率与理论分析的差异，本文进一步统计了AMAC中涉及矩阵求逆、乘法、加法等计算的耗时情况，发现32阶MMPA方法中计算矩阵(At-cI)-1的耗时与16阶CRAM方法中进行矩阵αi(At+θiI)-1的计算耗时相当，但在矩阵{(At+cI)(At-cI)-1}i的迭代相乘计算中，耗时较为严重，约6次矩阵(At+cI)(At-cI)-1的自迭代相乘与矩阵αi(At+θiI)-1的计算耗时相当，从而导致32阶MMPA方法在实际计算效率上没有显著优于16阶CRAM方法。本文尝试使用C++矩阵处理库Eigen替换AMAC中自编写的相关矩阵计算函数后，重新计算了OECD/NEA沸水堆组件燃耗基准题，发现32阶MMPA方法相比于16阶CRAM方法能加速约30%，加速效果较为显著，但应用于实际燃耗计算中还需大量的测试和程序优化，后续工作中对于AMAC中矩阵的计算效率需重点研究与优化。

4 结论

本文研究了一种基于最佳一致逼近多项式(MMPA)的燃耗计算方法。相比于CRAM和QRAM在求解中的多次复矩阵求逆，该方法仅需1次矩阵求逆即可求解燃耗方程，且所有计算皆为实数运算，数值稳定性好且求解效率高。同时基于MMPA方法开发了点燃耗程序AMAC，并与OpenMC进行耦合。为验证MMPA方法的正确性和有效性，基于AMAC对衰变问题和固定辐照问题进行了点燃耗测试，并与ORIGEN-2和RMC的计算结果进行了比较，结果吻合良好且计算效率较高。基于OpenMC-AMAC对OECD/NEA压水堆栅元燃耗基准题和沸水堆组件燃耗基准题分别进行了计算分析，计算结果与实验值及各参考值吻合良好，且与Serpent所采用的16阶CRAM的燃耗计算效率和精度相当。上述例题及基准例题的计算验证了MMPA方法在理论和数值上的正确性和有效性。后续工作将重点优化程序中的矩阵计算效率，进一步提高MMPA方法的计算效率。