基于分离变量的地震PSA相关性分析方法研究
冯丙辰,杨建峰,张晓明,王 照
(苏州热工研究院有限公司,广东 深圳 518000)
福岛事故后,核电厂外部灾害风险分析越来越受到业界的重视[1-2]。地震概率安全评价(PSA)作为一种定量评价核电厂地震风险的分析方法,已逐步在核电厂的设计和运行中得到应用[3-4]。随着不断地研究和实践,地震PSA方法已逐渐发展成熟,国内外相关技术导则[5]也陆续发布,用于指导地震PSA的开发和应用。
与内部事件PSA相比,地震PSA有两个显著特点[6]:1) 构筑物、系统和部件(SSC)的失效概率与地震的级别有关,需考虑核电厂所有可能发生的地震动范围及其影响后果;2) 地震可能同时对多个冗余或相似的SSC造成破坏,地震PSA定量化过程中需合理考虑这种相关性的影响。对于第1个特点,通过开发体现SSC不同地震动下条件失效概率的易损度曲线和体现厂址不同等级地震超越频率的危险性曲线,对两者进行卷积分[7]计算实现。但对于第2个特点,目前仍缺乏一套完善的处理方法。现有地震PSA中SSC相关性处理一般采用简化的假设[8]:位于相同位置(如相同厂房、高度、系统)相互冗余的同类设备相关性为1,其余相关性为0。该方法将系统冗余列中的设备按完全相关处理,通常情况下被认为是保守的。然而,对于可能存在部分相关性的情况,如不同系统中的相同设备,该方法认为其完全不相关,由此得到的结果将不保守甚至错误。
为更好地体现地震情况下SSC相关性的影响,本文对基于分离变量的易损度相关性分析方法开展研究,并对其在地震PSA中的应用进行讨论。
1 地震易损度评价
1.1 易损度模型
SSC的地震易损度定义为在确定的失效模式和给定地震动参数值(通常为峰值地面加速度PGA)下的条件失效概率。地震易损度评价的目的是确定SSC的抗震能力。抗震能力是一个随机变量,由概率分布来描述[9]:
A=AmeReU
(1)
式中:A为SSC的抗震能力;Am为抗震能力中值;eR和eU是中值为1的随机变量,分别代表随机性和不确定性。易损度采用双对数正态分布模型[10],即假设eR和eU分别服从对数标准差为βR和βU的对数正态分布。
在给定失效模式和Am的情况下(仅考虑随机性βR),对于给定的加速度a,SSC的条件失效概率f0可表示为:
f0=Φ[ln(a/Am)/βR]
(2)
式中,Φ[·]为标准正态累积分布函数。
当包含不确定性βU时,易损度成为一不确定的随机变量。对于给定的加速度a,易损度f可用主观概率密度函数表示。不超越易损度f′的主观概率Q(也称为置信度)和f′的关系如下:
(3)
式中:Q=P[f A=AmeΦ-1(f′)βRe-Φ-1(Q)βU (4) 地震易损度评价要确定SSC的易损度参数Am、βR和βU,从而开发易损度曲线。计算易损度参数一般用中间随机变量安全因子F[12],SSC的抗震能力可表示为: A=FASSE (5) 式中,ASSE为设计要求的安全停堆地震地面加速度能力。 设备的安全因子F可表示为: F=FCFSRFRE (6) 式中:FC为能力因子;FSR为结构响应因子;FRE为设备响应因子。 影响结构响应变化的变量包括谱形(SA)、地震动空间变化(GMI)、阻尼(δ)、模型(M)、模态组合(MC)和土壤与结构相互作用(SSI)。利用这些变量可计算结构响应因子及相应的随机性和不确定性[13]: FSR=FSAFGMIFδFMFMCFSSI (7) (8) (9) FC和FRE也可类似地分解为不同的变量来计算。 对于抗震能力中值Am,有: Fm=Am/ASSE (10) 式中,Fm为安全因子中值。由此,可通过计算F的中值Fm及随机性和不确定性获得Am、βR和βU。 目前地震PSA中采用简化假设的主要原因是难以获取相关性参数,缺乏相关性分析的输入。基于分离变量的相关性分析方法(以下称分离变量法)能避免直接求解相关性参数的问题,而是将其转化为易损度分析中相关变量的识别,易损度分析人员完全有能力对此进行判断[14]。 基于分离变量的地震相关性分析原理由Reed和McCann于1985年提出[14],通过在地震易损度评价中分离独立和相关变量来实现,与易损度评价过程紧密结合。这些变量为影响FC、FSR和FRE的各参数。通过识别这些参数是否具有相同的来源,来确定其为独立变量或相关变量。例如,假设两个不同设备位于相同厂房的相同位置,则它们具有相同的FSR及其随机性和不确定性,具有不同的FRE及其随机性和不确定性。 利用文献[14]中给出的原理和步骤,对分离变量法计算模型进行推导。 对相关性的考虑,一种易于理解的处理方式为将设备失效概率P分解为独立失效的贡献P′和相关失效的贡献P* [15],有: P=P′+P* (11) 结合式(4),设备的抗震能力可表示为: A=A′x (12) 式中:A′为抗震能力独立的部分;x为相关的部分。 分离变量法分为两个阶段,其流程如图1所示。 (13) 图1 分离变量法分析流程Fig.1 Procedure of separation of variables method (14) 根据式(2),在给定的a下设备A和B独立失效的条件概率可分别表示为: (15) (16) 在区间(x,x+Δx)上,A和B同时失效的概率为: (17) 式中,p(x)为x的概率密度函数。对x进行积分,可得在给定的a下A和B联合失效的条件概率为: (18) 改变a,利用式(18)对第1阶段中选取的每组抗震能力中值重复上述过程,可得到联合失效的易损度曲线族。 选取某CPR1000核电厂地震PSA中的3组典型设备开展案例分析,表1和表2列出了每组设备的易损度参数和相关性信息[16]。其中,按已有简化假设,案例a中应急柴油发电机组相关性为1,案例b中APU机柜和PIPS机柜相关性为0,案例c中LHB配电盘和LLB配电盘相关性为0。 表1 案例分析设备易损度信息Table 1 Equipment fragility of case study 表2 案例分析设备易损度参数信息Table 2 Equipment fragility variables of case study 续表2 采用分离变量法,对上述3组设备开展相关性分析,得到联合失效的易损度曲线。图2示出了分离变量法计算联合失效5 000次抽样的均值易损度曲线,及其与简化假设结果的对比。 图2 联合失效易损度曲线案例分析结果Fig.2 Fragility curve of joint failure of case study 根据联合失效的易损度曲线,利用图3示出的CPR1000核电厂厂址地震危险性分析结果,两者卷积得到地震情况下核电厂设备联合失效的频率。表3列出了分离变量法和简化假设联合失效频率的结果对比。 图3 CPR1000核电厂厂址均值地震危险性曲线Fig.3 Mean seismic hazard curve of CPR1000 NPP site 表3 联合失效频率案例分析结果Table 3 Result of case study for joint failure frequency 从结果可看出,与现有简化假设相比,案例a中考虑厂房结构差异后利用分离变量法得到的结果有所降低,案例b和c中考虑部分相关性后利用分离变量法得到的结果有所增加。总体上,分离变量法能更细致地体现核电厂SSC之间的相关性,避免现有简化假设过于保守(案例a)和未考虑部分相关性的情况(案例b和c)。尤其是后者,如果地震PSA支配性割集中存在该类问题,简化假设得到的结果会偏不保守甚至错误,而分离变量法能有效避免这类错误。同时,对于完全相关和完全不相关的情况,分离变量法同样能处理,与现有简化假设相比,具有更普遍的适用性。 分离变量法与地震易损度评价过程密切相关,需易损度分析人员根据影响抗震能力的各变量,结合设计、鉴定和安装等信息识别并确定SSC之间的相关性。同时,该方法得到的结果由易损度曲线族来表示,包含了SSC联合失效的随机性和不确定性,可直接用于地震PSA的定量化分析。 需说明的是,地震PSA中完全采用分离变量法处理SSC的相关性并不现实,一是由于方法的复杂性导致分析过程繁琐、工作量大,二是不同的相关性处理并非对所有事故序列、割集造成显著差异。可根据已有地震PSA的结果,开展敏感性分析,识别不同相关性分析方法对结果影响显著的事故序列或割集,针对这些事故序列或割集利用分离变量法开展详细的相关性分析,更新地震PSA的结果。 对基于分离变量的地震PSA相关性分析方法进行了研究,根据不同的相关情况开展了案例分析。结果表明,与现有相关性简化假设相比,分离变量法能更好体现SSC之间的地震相关性。同时,对该方法在地震PSA中的应用提出了建议。1.2 易损度参数估计
2 基于分离变量的相关性分析方法
2.1 方法原理
2.2 计算模型


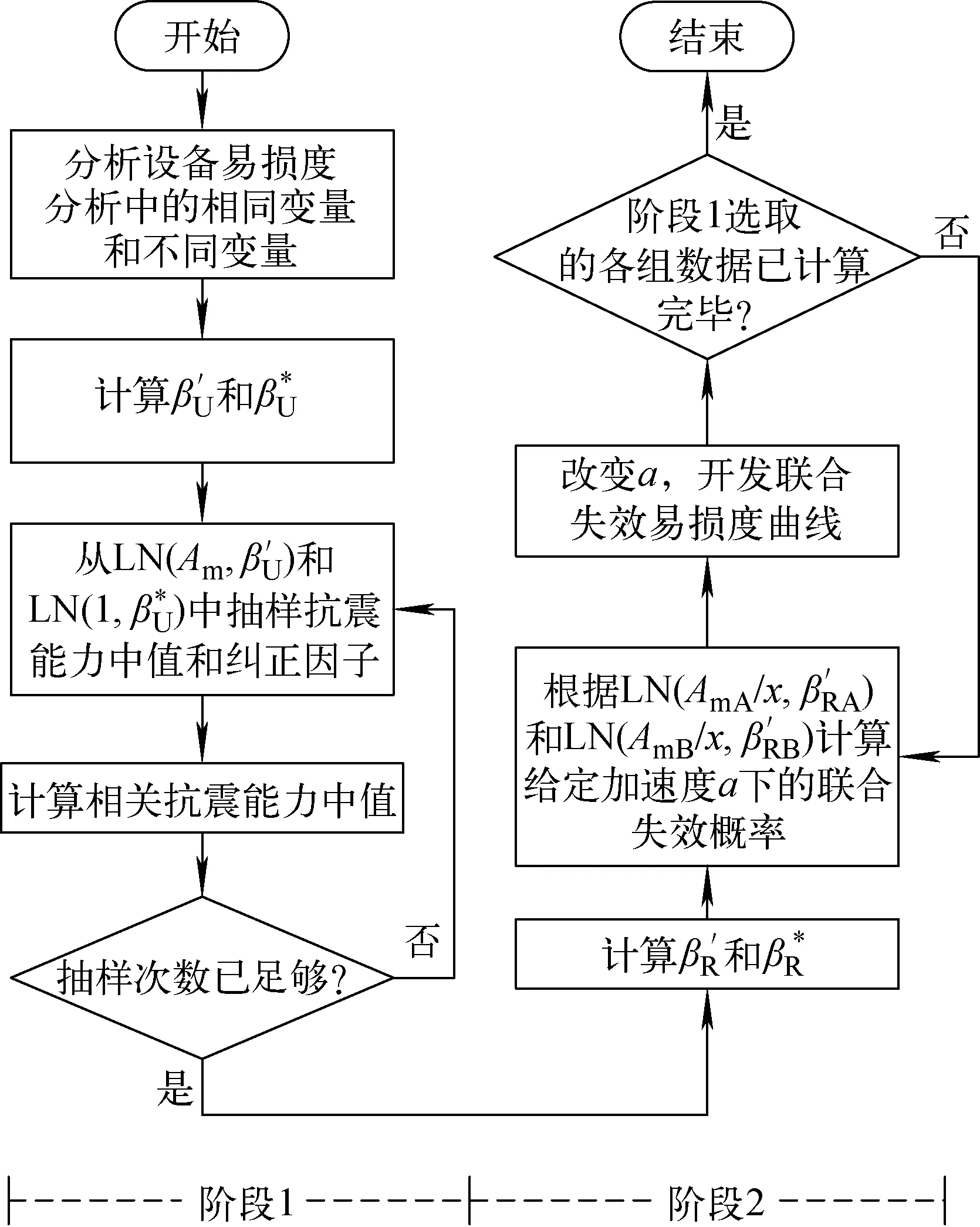

3 案例分析


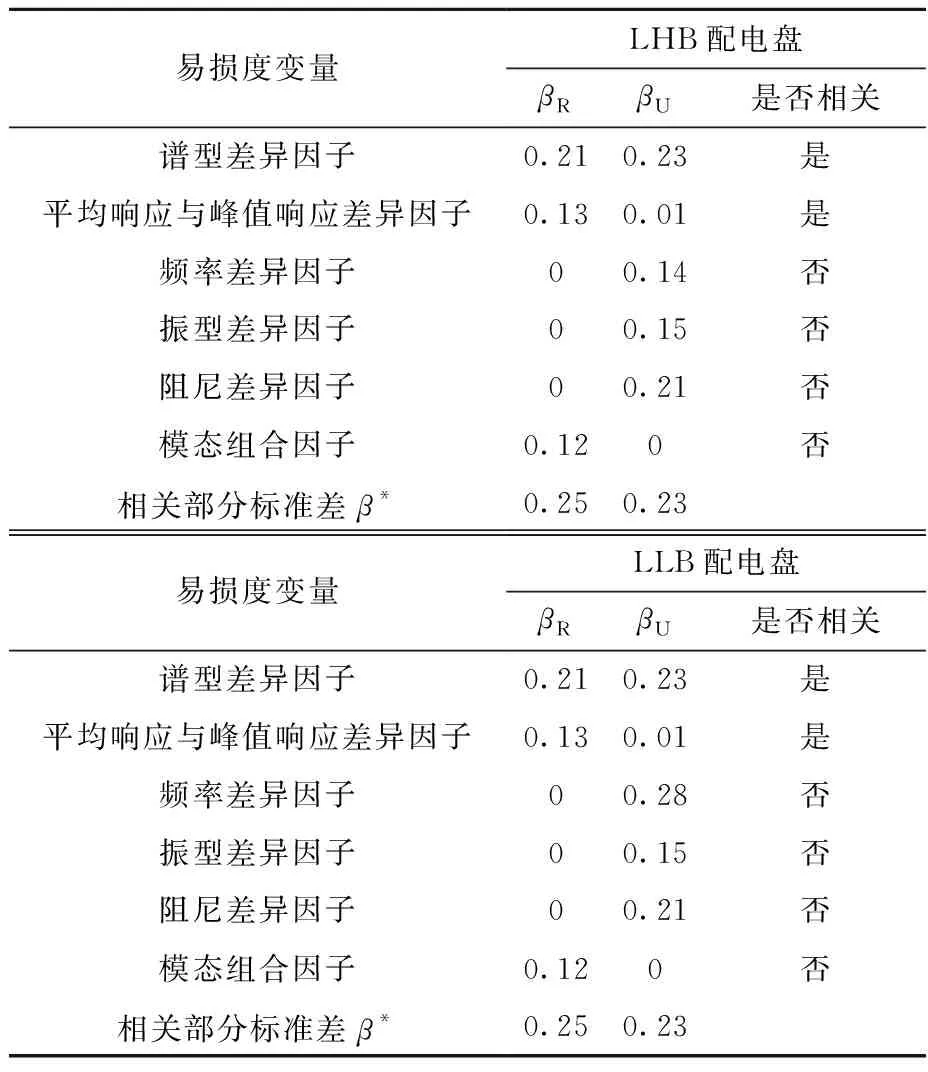



4 地震PSA中的应用
5 结论

