燃气锅炉主汽压的RBF神经网络滑模控制策略设计

王 胜，章家岩，冯旭刚

(安徽工业大学 电气与信息工程学院，安徽马鞍山 243032)

主蒸汽压力( 简称主汽压)是表征锅炉运行状况的重要被控参数，是衡量锅炉蒸汽产量与负荷是否匹配的重要指标，它反映了锅炉燃烧过程中的能量供求关系。对于燃气锅炉，燃烧控制系统的主要任务是根据汽轮机负荷变化来实时调整锅炉的燃料供应量，保持锅炉主汽压等被控参数的稳定，这对于保证火电机组锅炉设备的安全稳定运行，实现节能降耗和降本增效，提高企业经济效益都具有重要意义[1-3]。

锅炉运行过程中，主汽压发生变化说明其产汽量与汽轮机的耗汽量不匹配，对于燃气锅炉，应该实时调整燃气供应量，使得产汽量跟随耗汽量的变化而变化，从而保证锅炉主汽压的稳定。但由于燃气锅炉采用的燃料大都是钢铁企业生产过程中产生的高炉煤气和转炉煤气，其压力和热值波动较大，导致主汽压难以稳定控制，常规的控制方法难以达到理想的控制效果。Ma等[4]针对主汽压研究了12输入3输出的径向基函数(RBF)神经网络控制，有效提高了锅炉负荷响应速率和自适应能力，但由于该网络输入输出数量较大，导致网络学习速度下降。Shi等[5]采用基于Smith预估结构的滑模控制，将内模控制和Smith预估器相结合处理主汽压的时变问题，有效克服了对象的模型失配问题，但由于系统状态测量存在误差且缺少对误差的补偿，导致波形抖动。Wang[6]采用模糊神经网络实现了主汽压的自适应和自学习控制，具有实时在线调节的能力，但由于其设计的模糊化和解模糊过程较为粗糙，导致波形抖动较大，控制精度降低。

为此，笔者以燃气锅炉主汽压为控制对象，提出了一种基于神经网络和滑模控制相结合的主汽压优化控制策略，并引入干扰观测器实现对不匹配扰动的补偿。利用神经网络的自学习和自适应能力对滑模控制的切换增益进行及时调整，并通过仿真来验证该控制算法的有效性。

1 主汽压控制系统构建

1.1 控制系统原理分析

燃气锅炉燃烧控制系统如图1所示，整个燃烧过程主要涉及燃料、送风和引风3个子环节[7-8]。高炉煤气、转炉煤气和焦炉煤气是燃气锅炉的主要燃料来源[9]，根据锅炉负荷的变化合理调整锅炉燃烧器的煤气供给量是保证锅炉主汽压稳定的关键。但由于冶金行业的高炉炼铁和转炉炼钢生产工艺具有间歇性的特点，且整个煤气供应管网生产用户(如轧钢加热炉、炼铁热风炉)众多，会造成煤气产耗有很大的不确定性，导致供给锅炉燃烧的煤气压力波动显著，这也是煤气流量的主要扰动源。因此，为保证燃烧过程的经济性和生产的安全性，在控制主汽压的同时，还要保持最佳空燃比和炉膛负压的稳定，即当煤气供应量改变时，送风量和引风量也要进行相应调整。

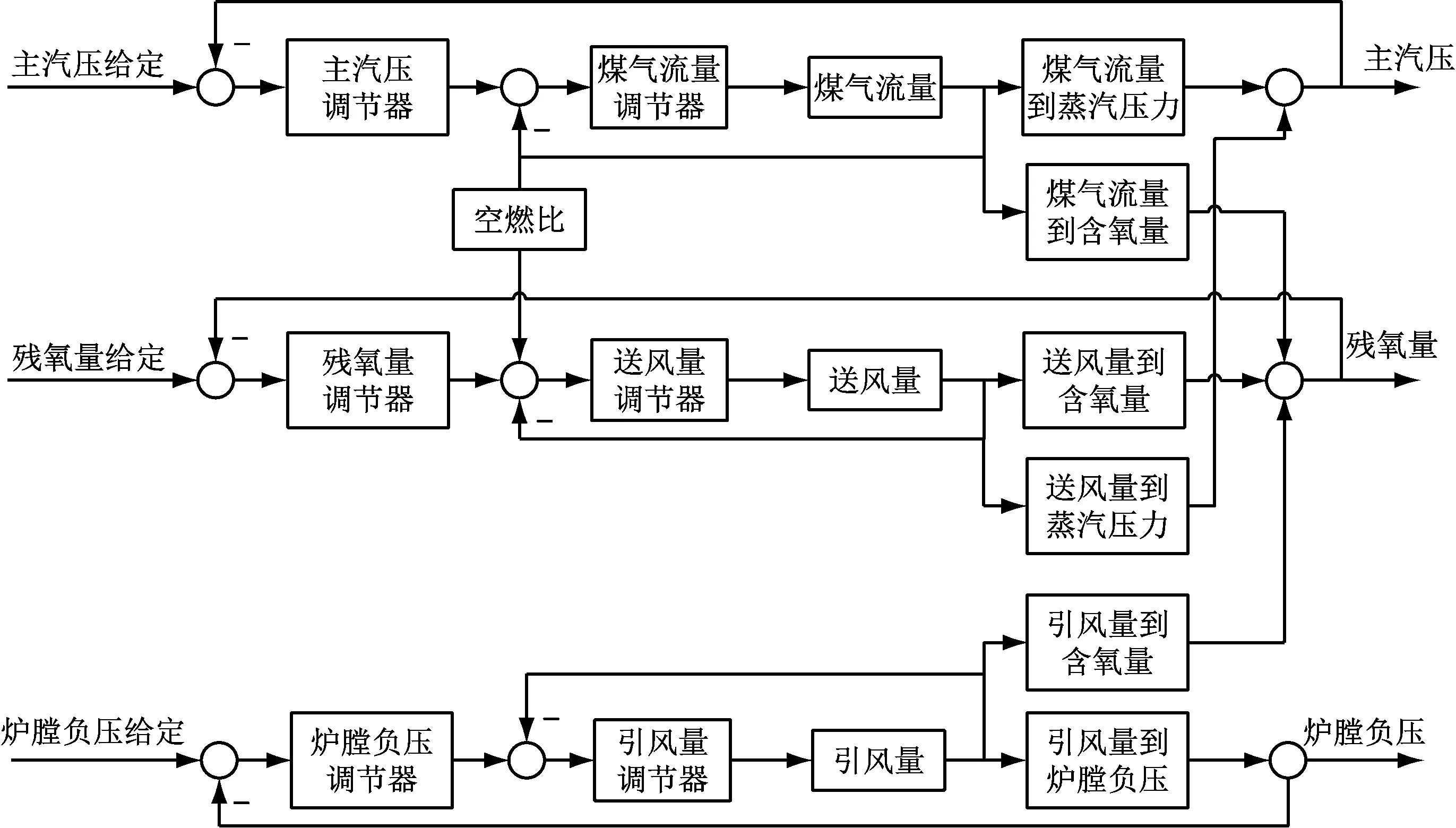
图1 燃气锅炉燃烧控制系统

1.2 主汽压控制回路设计

针对燃气锅炉主汽压控制的非线性、干扰大和模型参数易变的特点，笔者采用干扰观测器、神经网络滑模控制器和非线性补偿器对主汽压调节实现前馈、滑模串级主调和非线性补偿控制，控制回路设计方案如图2所示。图中，锅炉主汽压信号y通过变送器转换成4～20 mA的信号反馈至控制器输入端，该电信号与生产现场主汽压设定值SV之间形成偏差信号e，RBF神经网络滑模控制器以偏差信号输出的控制量作为副回路的设定值，副回路通过调节煤气流量阀门(阀门已进行非线性补偿)开度来改变煤气流量，并利用干扰观测器对煤气流量扰动进行前馈补偿，从而提高锅炉主汽压控制系统的稳定性，工程实践一般要求锅炉主汽压稳定在设定值的±5%。

图2 燃气锅炉主汽压控制总体方案Fig.2 Overall plan for main steam pressure control of the gas-fired boiler

针对主汽压控制系统的非线性特点，采取以下措施:

(1) 对煤气流量阀门的控制信号占空比进行非线性补偿，以改善阀门流量的非线性特性。电液数字阀门的流量特性由死区、线性区和饱和区三部分组成，对死区和饱和区的控制信号占空比进行补偿，补偿公式分别为式(1)和式(2)。

(1)

(2)

式中：t1、t2、t3和t4分别为阀芯的吸合延迟时间、吸合运动时间、释放延迟时间和释放运动时间，ms；T为阀门控制信号周期，ms；D为控制器输出的控制信号占空比；Dcom为补偿后的控制信号占空比。

以HSV-3101S1型电液数字阀门为例进行计算，对应的阀门控制信号周期T为30 ms，对其不同开度下的流量特性进行分析，得出t1=1.5 ms,t2=1 ms,t3=1.5 ms,t4=1 ms，则基于死区、线性区和饱和区的分段补偿控制信号占空比为：

(3)

(2) 将煤气流量控制放在串级系统的副回路，一方面可以很大程度地削弱煤气流量扰动的影响，另一方面可以克服因煤气流量扰动造成主汽压控制系统的非线性问题。

以上2点基本可以实现主汽压控制系统的近似线性化。

2 RBF神经网络滑模控制器设计

2.1 滑模控制器的设计

燃气锅炉主汽压控制系统的动态特性可以用含未知输入的动态状态方程来描述，即

(4)

对于式(4)，取切换函数为：

c1x1+…+cn-1xn-1+xn

(5)

其中，常数c1，c2，…，cn-1应满足多项式λn-1+cn-1λn-2+…+c2λ+c1为Hurwitz，则：

(6)

ueq=-(cB)-1(cAx+cBdt+cdtt)

(7)

式(6)可表示成：

cB(u-ueq)

(8)

(9)

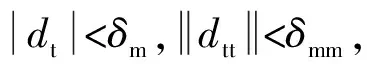
(10)

(11)

式中：K为滑模控制器的切换增益，K=(cB)-1σ。假设cB>0，则

(12)

u被确定后，系统状态轨迹将会在有限时间内到达滑模面，之后停留在滑模面滑动。滑模面上系统特征可以描述成：

Ax+B[-(cB)-1(cAx+cBdt+cdtt)]+Bdt+dtt=

Ax+dtt-B(cB)-1c(Ax+dtt)-Bdt+Bdt=

[I-B(cB)-1c](Ax+dtt)

(13)

式中:I为单位矩阵。

从式(13)可以看出，滑模面上的系统不受煤气流量匹配扰动dt的影响，且

(c-c)(Ax+dtt)=0

(14)

2.2 RBF神经网络滑模控制器设计

系统状态轨迹在滑模面上的抖振主要是由滑模控制器的切换增益K引起的，且K越大，系统抖振越厉害。利用神经网络的自学习、自适应能力对切换增益进行调节，可有效降低控制系统的抖振[10-12]。RBF神经网络滑模控制器的结构如图3所示。

图3 RBF神经网络滑模控制器Fig.3 RBF neural network sliding mode controller

K=|wTz(q)|

(15)

式中：z(q)为高斯函数；w为RBF神经网络隐含层到输出层的连接权值。

(16)

式中：Ci为网络第i个节点的中心向量；ri为网络基宽向量中的第i个值。

定义目标函数E为：

(17)

神经网络连接权值的调整算法为：

(18)

式中：η为神经网络学习速率，η∈(0,1)。

Δw≈-ηe(-1)sgn(s)z(q)sgn(wTz(q))

(19)

神经网络最终学习算法为：

w(t)=w(t-1)+Δw(t)+α[w(t)-w(t-1)]

(20)

式中：α为神经网络惯性系数，α∈(0,1)。

将神经网络的输出K值代入式(11)，则控制律为：

(21)

3 干扰观测器设计

由式(13)可知，滑模面上的系统不受煤气流量匹配扰动dt的影响，故设计干扰观测器时只需考虑煤气流量不匹配扰动dtt，针对式(4)的扰动问题，已有不少学者对其干扰观测器的设计进行了研究[13-15]，笔者选取简单有效的比例积分观测器。将式(21)作为基准控制律，引入干扰观测器后的复合控制律u*:

(22)

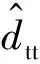
根据式(4)设计全阶比例积分观测器：

(23)

式(23)可表示成如下形式：

(24)

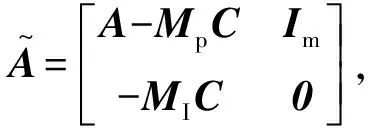
式(23)设计的全阶比例积分观测器的观测性能和存在性有如下引理：

成立。

4 仿真分析

为了验证上述优化算法的有效性，选取某热电厂150 t燃气锅炉主汽压作为仿真对象，100%负荷下其状态空间表达式为：

(25)

4.1 滑模控制器相轨迹仿真对比

系统的设定值SV取幅值为1的正弦波信号，图4(a)为常规滑模控制器的相轨迹，图4(b)为RBF神经网络滑模控制器的相轨迹。

(a) 常规滑模控制器

(b) RBF神经网络滑模控制器图4 2种控制器的相轨迹Fig.4 Phase trajectories of two controllers

对比图4(a)和图4(b)可知，常规滑模控制器相轨迹抖振明显，尤其在平衡点附近时抖振幅度达到了±0.5，波动较大。而RBF神经网络滑模控制器在平衡点附近时抖振幅度为±0.2，系统抖振幅度较常规滑模控制器降低了60%，说明神经网络对滑模控制器的切换增益K具有良好的优化效果，能实时给出最优切换增益，降低系统抖振。

4.2 滑模控制器跟随及抗干扰性能仿真对比

在[-1,1]的随机干扰下，图5(a)为采用常规滑模控制的方波和正弦波跟随曲线，跟随误差在[-0.2,0.2]，跟随性能一般。图5(b)为采用带干扰观测补偿的滑模控制的方波和正弦波跟随曲线，与常规滑模控制相比，系统的跟随性能明显改善，其随机干扰得到了有效抑制，但是在给定方波信号发生阶跃跳变的时刻，跟随曲线产生较大的尖峰，而正弦波跟随曲线仍然存在一定的跟随误差，误差基本在[-0.1,0.1]。图5(c)为采用带干扰观测补偿的RBF神经网络滑模控制，用方波与正弦波的叠加信号作为其跟随设定信号，在神经网络得到有效学习之后，设定信号与跟随曲线几乎完全重合，系统的随机干扰和阶跃跳变时产生的尖峰被有效克服。

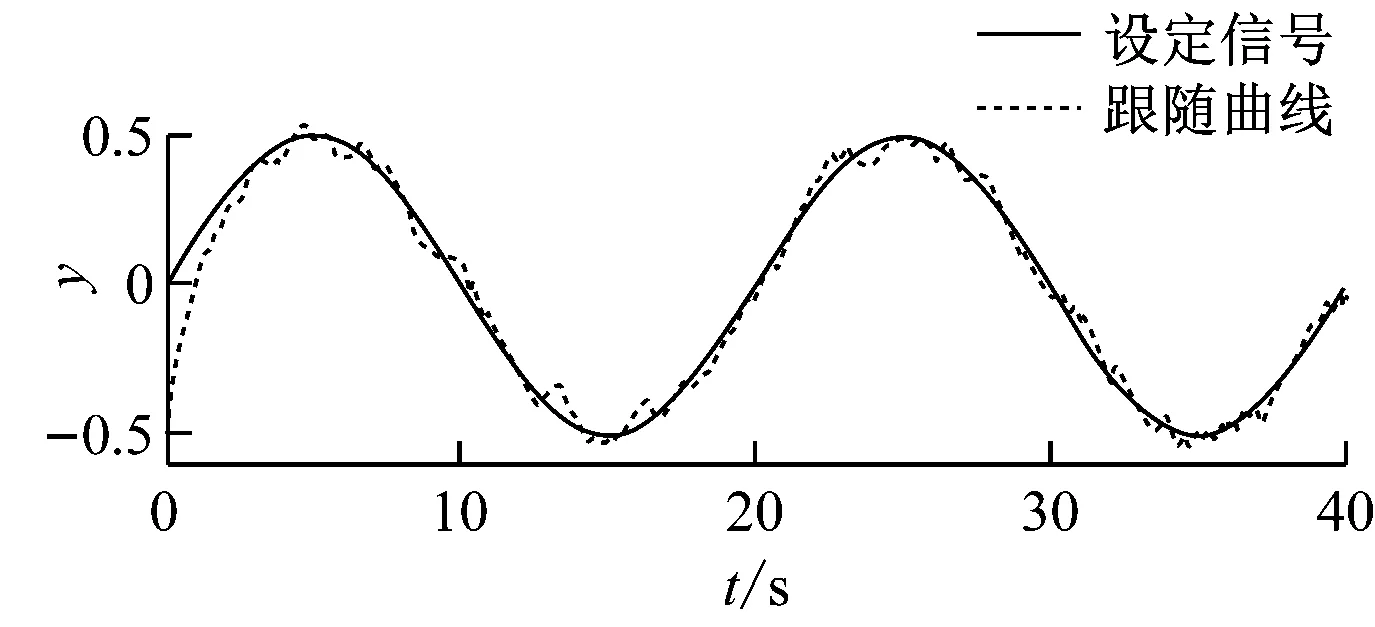
(a) 常规滑模控制

(b) 干扰观测补偿的滑模控制

(c) 干扰观测补偿的RBF神经网络滑模控制图5 3种控制策略的跟随曲线Fig.5 Following curves of three control strategies

4.3 滑模控制器鲁棒性仿真

用同样的系统辨识方法得到80%负荷下锅炉主汽压的状态空间表达式为：

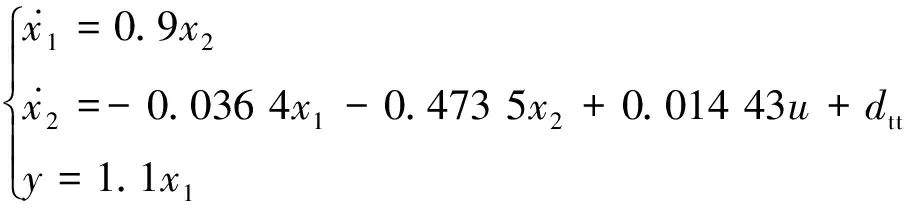
(26)

为观察设计控制策略的鲁棒性能，分别对100%负荷和80%负荷下锅炉主汽压对象进行阶跃响应仿真，主汽压设定值为6 MPa，系统运行135 s时加入幅值为20%的阶跃扰动dtt。

图6(a)和图6(b)分别为100%负荷和80%负荷下3种控制策略的阶跃响应曲线，根据经验试凑法，100%负荷下比例积分微分(PID)参数取为KP=0.12,KI=0.083,KD=4.11，80%负荷下KP=0.15,KI=0.09,KD=3。从图6可以看出，100%负荷下常规PID控制的调节时间为110.24 s，超调量为4.17%，主汽压波动范围在-0.086～0.21 MPa；常规滑模控制的调节时间为112.32 s，超调量为2.1%，主汽压波动范围在-0.056～0.15 MPa；带干扰观测补偿的RBF神经网络滑模控制的调节时间为54.87 s，超调量为1.56%，主汽压波动范围在-0.046～0.1 MPa，相比常规PID控制和常规滑模控制，主汽压控制精度分别提高了51.7%和30%。80%负荷下常规PID控制的调节时间为100.38 s，超调量为8.24%，主汽压波动范围在-0.086～0.35 MPa；常规滑模控制的调节时间为80.13 s，超调量为2.05%，主汽压波动范围在0.046～0.1 MPa；带干扰观测补偿的RBF神经网络滑模控制的调节时间为45.67 s，超调量为1.62%，主汽压波动范围在-0.026～0.11 MPa，相比常规PID控制和常规滑模控制，主汽压控制精度分别提高了69.8%和7.1%。基于以上分析可知，带干扰观测补偿的RBF神经网络滑模控制的鲁棒性明显优于常规PID控制和常规滑模控制，且系统调节过程中所需时间更短，超调量更小，控制精度更高。2种工况下，带干扰观测补偿的RBF神经网络滑模控制策略超调量最多减少6.62%，调节时间最多减少57.45 s，其抗干扰性能均优于另外2种控制策略。

5 工程应用

为检验系统实际应用效果，将带干扰观测补偿的RBF神经网络滑模控制策略应用于某热电厂150 t燃气锅炉主汽压控制中，控制系统为和利时集散控制系统(DCS)系统，整个优化控制系统拓扑结构如图7所示。在该控制系统中，压力变送器将检测到的主汽压送到DCS系统，带干扰观测补偿的RBF神经网络滑模控制器利用检测到的主汽压、煤气压力和汽轮机耗汽量等耦合因素计算出煤气供应量，进而调节煤气流量阀门。系统的设计以生产管理层作为中央操作站。逻辑控制层采用s7-300PLC作为控制器，对现场采集到的数据进行处理。生产现场层负责锅炉燃烧供汽过程中现场信号的采集和输出。操作监控层则负责整个系统运行状况的监控。

(a) 100%负荷

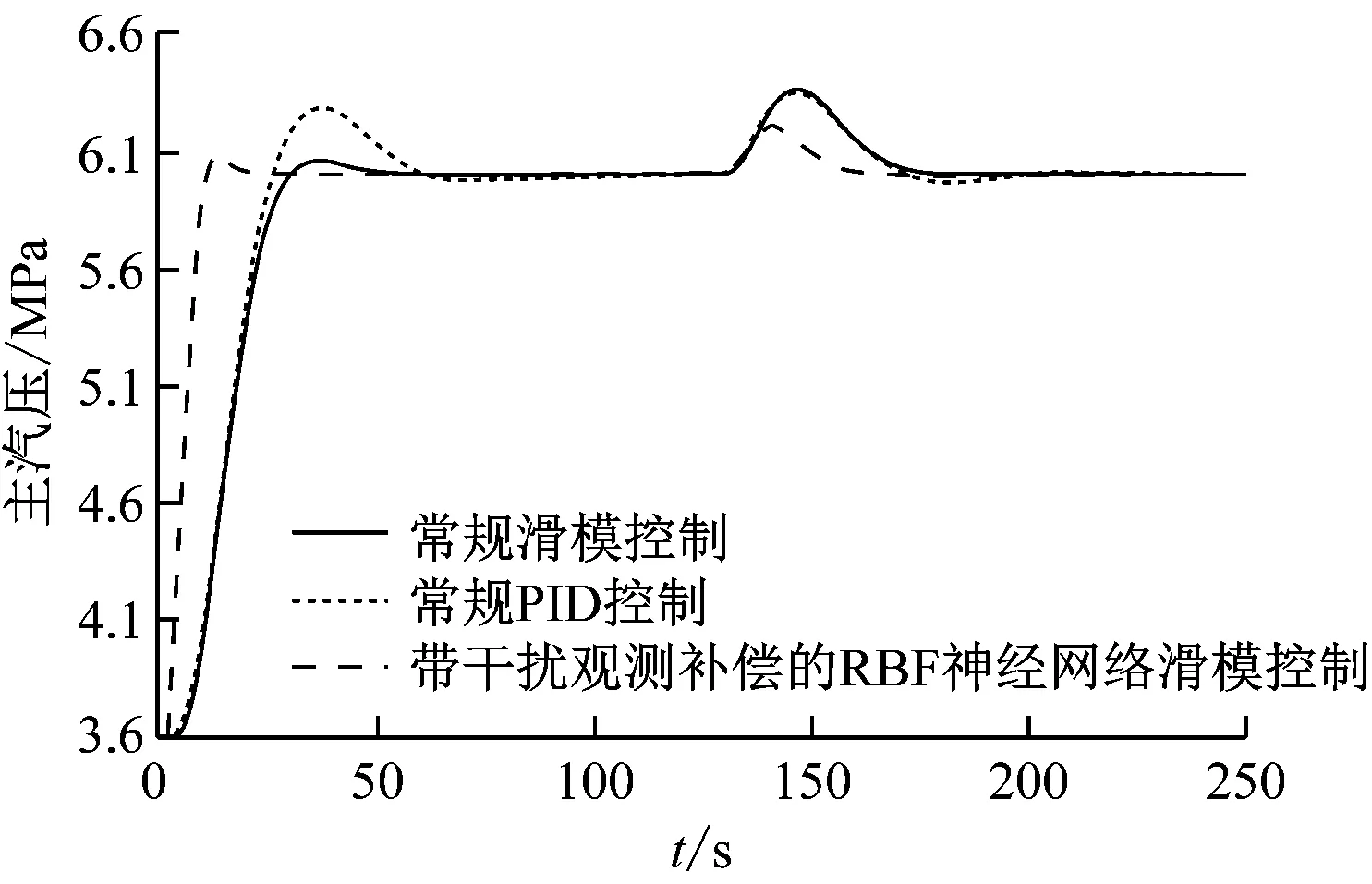
(b) 80%负荷图6 2种负荷下的阶跃响应Fig.6 Step response under two load conditions

图7 优化控制系统结构Fig.7 Structure of the optimized control system

图8(a)～图8(c)给出了锅炉100%负荷下连续3 d分别采用常规滑模控制、RBF神经网络滑模控制和带干扰观测补偿的RBF神经网络滑模控制的主汽压实时曲线，观察时间为4 h。从图 8可以看出，采用常规滑模控制时主汽压波动范围在±0.3 MPa，采用RBF神经网络滑模控制时主汽压波动范围在±0.2 MPa，系统抖振较常规滑模控制降低了33%，显然神经网络优化了滑模控制器的切换增益。将带干扰观测补偿的RBF神经网络滑模控制作为主汽压的控制策略时，主汽压波动范围在±0.1 MPa，控制精度较RBF神经网络滑模控制和常规滑模控制分别提高了50%和66.7%，系统扰动得到了有效遏制。而仿真时RBF神经网络滑模控制较常规滑模控制的系统抖振幅度降低了60%，采用常规滑模控制和带干扰观测补偿的RBF神经网络滑模控制时的主汽压波动范围分别在-0.05～0.15 MPa和-0.04～0.1 MPa，工程实际应用效果比仿真结果略差，这主要是因为实际生产现场环境复杂多变，存在很多不确定性的干扰因素。

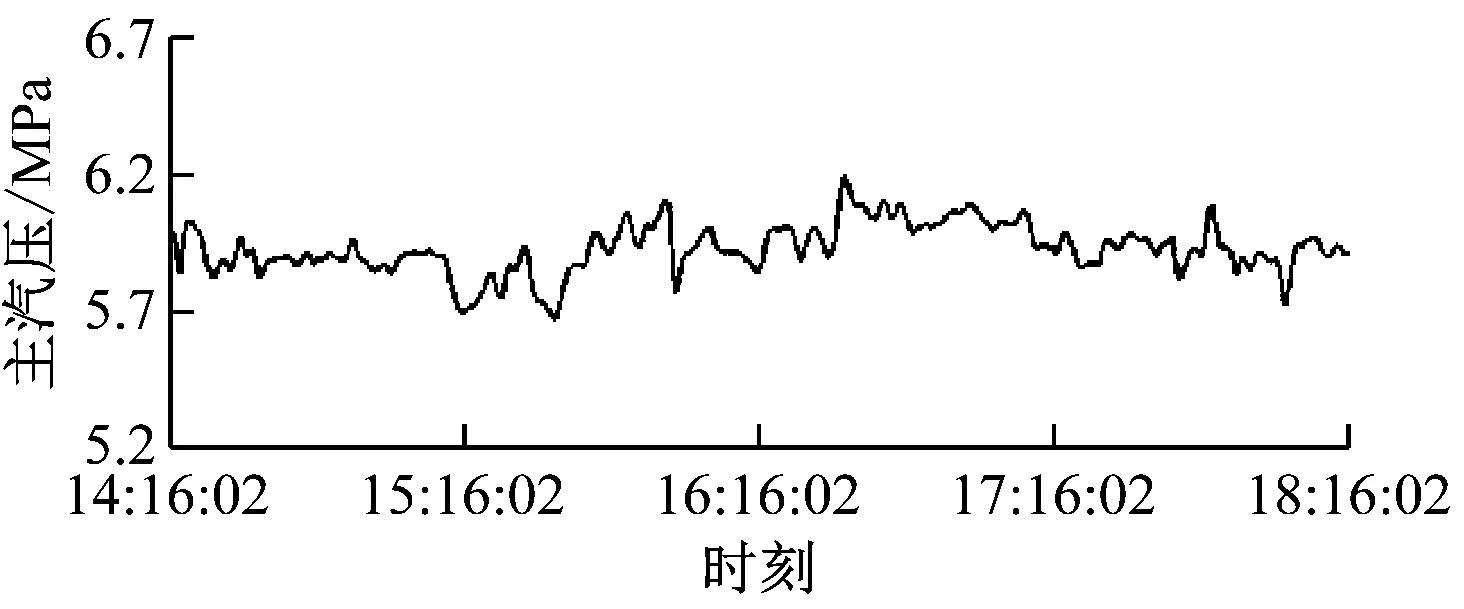
(a) 常规滑模控制

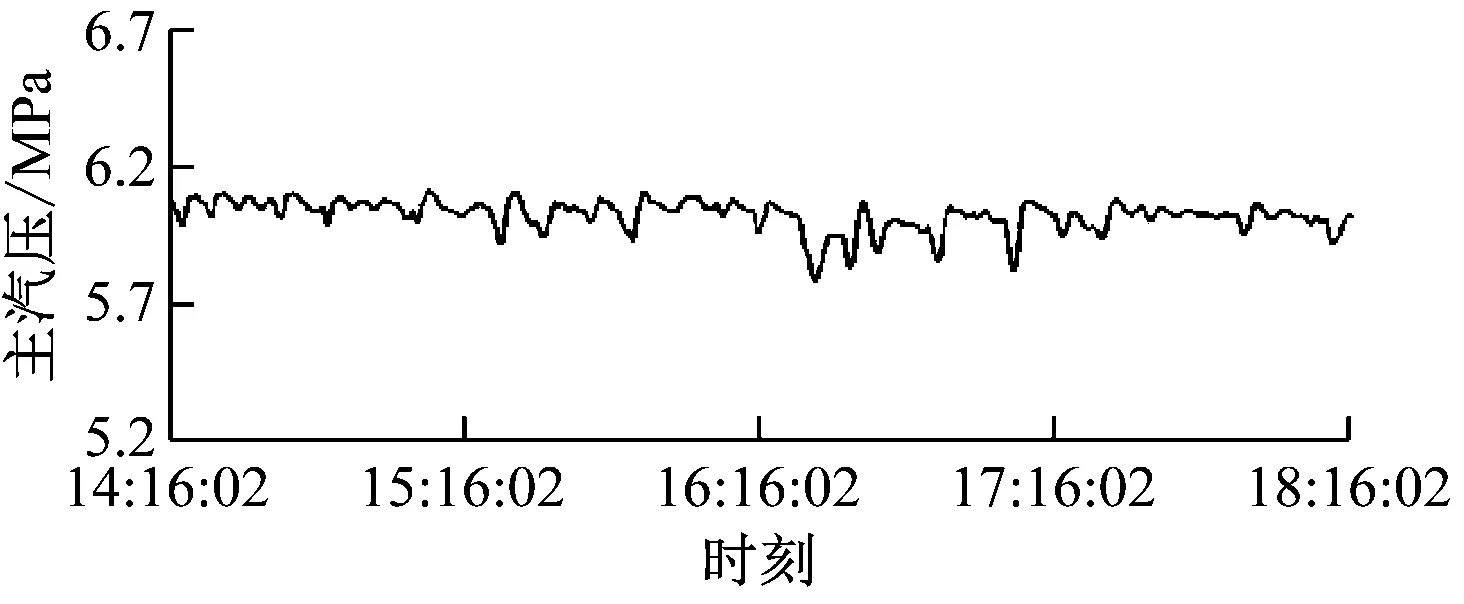
(b) RBF神经网络滑模控制

(c) 带干扰观测补偿的RBF神经网络滑模控制图8 3种控制策略下的主汽压曲线Fig.8 Main steam pressure curve under three control strategies

基于以上分析，所提出的带干扰观测补偿的RBF神经网络滑模控制策略提高了主汽压控制的稳定性能，达到了良好的控制效果。

6 结 论

(1) 本文设计了带有干扰观测补偿的RBF神经网络滑模控制策略。利用神经网络自学习、自适应能力来调节滑模控制器的切换增益，有效降低了系统抖振，加入干扰观测器后的复合控制提高了系统的抗干扰能力。

(2) Matlab仿真结果表明，所设计的控制策略抖振小，跟随性能好，在超调量和调节时间方面优于常规PID控制和常规滑模控制，具有更强的鲁棒性和抗干扰能力。

(3) 将该优化控制策略用于某热电厂燃气锅炉中，主汽压控制偏差在-0.04～0.1 MPa，有效提高了发电机组运行的安全性和稳定性。