水轮机空化声发射信号的优化VMD特征提取

刘 忠，刘 振，邹淑云，陈 莹，蒋 盈

(1．长沙理工大学 能源与动力工程学院，长沙 410114；2．中国水利水电科学研究院，北京 100038)

空化会破坏水流正常的流动状态，降低水轮机的水力性能，严重时会导致过流部件损坏，造成机组严重振动，产生噪声，威胁水电站的安全经济运行[1]。水轮机空化过程中大量微型射流或冲击波作用于叶片和管壁，形成包含0.02～1 MHz的高频声发射(Acoustic Emission，AE)信号，并沿着水力、机械系统进行传播[2]。对伴随空化产生的AE信号进行有效检测与特征提取，有望实现对空化状态的监测和辨别。国内外学者对水轮机空化产生的非平稳、非周期的AE信号进行了诸多研究。Husin等[3]证实了在气液两相流动条件下将声发射技术应用于气泡的在线检测是可行的。Rus等[4]在轴流式低水头闭环试验台上进行试验，揭示了AE信号的叶片流道调制水平相对值与空化系数的关系。刘忠等[5-6]采用小波包方法和改进经验模态分解(Empirical Mode Decomposition，EMD)对混流式模型水轮机空化声发射信号进行了特性分析，揭示了各典型频段小波包能量和各本征模态函数(Intrinsic Mode Function，IMF)特征分量随空化系数的变化规律。但小波包在变换算法上并没有取得明显突破，仍然受限于小波基和分解层数的选择，而EMD及其改进算法(EEMD)仍然存在因极值点包络估计误差易出现模态混叠和端点效应，参数难以选择，重构信号中存在残余噪声等问题[7]。

变分模态分解(Variational Mode Decomposition，VMD)[8]方法通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，具有更坚实的理论基础，因此得到了广泛应用。但VMD算法中分解层数和惩罚因子需要预先设定，极大地影响了分解效果。李华等[9]采用峭度最大值优化VMD分解层数的方法对滚动轴承早期故障进行了特征提取，但仅考虑了分解层数优化而将惩罚因子设为定值。Shi等[10]采用独立优化VMD参数的方法对风力机进行了状态监测，却忽略了分解层数与惩罚因子的内在联系，易使迭代算法陷入局部最优。为了实现全局寻优，蝗虫优化算法[11]、多目标粒子群算法[12]等已被用于VMD参数组合优化。灰狼优化(Grey Wolf Optimization，GWO)[13]算法是一种模拟灰狼种群捕食行为机制和种群等级制度的智能元启发式优化算法，具有收敛性较强、设置参数较少和易实现等优点，但这一方法容易陷入局部最优解。布谷鸟搜索(Cuckoo Search，CS)[14]算法是模拟布谷鸟的寄生育雏行为与莱维飞行搜索机制相结合而形成的一种有效求解最优化问题的算法，具备很强的全局搜索能力。笔者结合灰狼优化算法与布谷鸟搜索算法，对VMD的分解层数和惩罚因子参数进行全局组合搜寻，形成了GWO和CS混合优化VMD算法(简称优化VMD算法)，并将其应用于水轮机空化AE信号的特征提取中。

1 基本理论

1.1 VMD算法

VMD 算法实际上是一个变分问题的求解过程。其将信号f分解为k个模态函数uk，且每个IMF具有固定的中心频率ωk，使得每个模态函数的估计带宽之和最小。其建立的约束变分模型为：

(1)

(2)

式中：δ(t)为冲击函数。

为了将上述约束性变分问题转变为非约束性变分问题，引入惩罚因子α和拉格朗日乘子λ(t)，惩罚因子α可以在有高斯噪声的情况下保证信号的重构精度，而拉格朗日乘子λ(t)则保证了约束条件的严格性，故扩展的拉格朗日表达式L为：

(3)

利用乘子交替方向算法不断更新各uk,n+1、ωk,n+1和λk,n+1，求得式(3)的鞍点即为原问题的最优解。利用Parseval/Plancherel傅里叶等距变换，将式(3)变换到描述频率ω特性的频域求解，模态uk和中心频率ωk可分别通过式(4)和式(5)进行更新。

(4)

(5)

VMD算法的具体步骤如下：

(1) 进行参数初始化，{uk,1}、{ωk,1}。

(2) 根据式(4)和式(5)在频域内更新uk和ωk。

1.2 灰狼优化算法和布谷鸟搜索算法

1.2.1 灰狼优化算法

在GWO算法中，为模拟灰狼种群的社会等级制度，定义狼群中的当前最优解为η，次最优解为β，第三最优解为φ，其他解均为v。

灰狼追捕包围猎物的数学模型为：

(6)

式中：D为灰狼与猎物间的距离；l为当前迭代次数；Xp为猎物的位置向量；X为灰狼的位置向量；A和C为协同系数向量。

其中,A和C的计算式为：

(7)

式中：r1、r2为[0,1]之间的随机向量；a值随迭代次数的增加从2到0之间线性减小。

在狩猎过程中，若η、β和φ灰狼知道猎物的位置，则灰狼群体就可以利用这三者的位置来判断猎物所在的方位。其数学表达式为：

(8)

(9)

式中：Xη、Xβ和Xφ为η，β和φ狼的当前位置；Dη、Dβ和Dφ为η，β和φ狼分别与猎物的距离。

1.2.2 布谷鸟搜索算法

CS算法的基本原理是把布谷鸟所寄生的鸟巢位置映射为算法的解，以寄生巢位置的优劣作为算法的适应度值，寻找鸟巢的位置是随机或者类似随机的方式。

布谷鸟寻找鸟巢路径和位置的更新表达式为：

xi(l+1)=xi(l)+γ⊕L(θ),i=1,2,…,n

(10)

式中：xi(l)为第i个鸟巢在第l次迭代后的位置；γ为步长控制量；⊕表示点对点乘积；L(θ)为列维分布函数，服从L～u=l-θ(1<θ≤3 )。

1.2.3 灰狼和布谷鸟混合优化算法

在GWO算法中，狼群始终根据η、β和φ狼的位置信息来更新自身位置，使其迅速向最优解聚集，但这容易导致整个狼群过早地聚集于当前最优位置的某一邻域内，从而陷入局部最优解。CS算法通过莱维飞行机制可随机更新鸟巢位置，跳出当前区域，全局搜索能力强。因此，笔者将GWO算法和CS算法进行混合优化，利用CS算法对适应度值最好的3只灰狼和整个种群进行位置扰动，让狼群在逼近猎物的过程中根据是否被发现的概率p随机地更新位置，使算法具备更强的全局搜索能力和更快的收敛速度，适应性更强。

GWO和CS混合优化算法流程图见图1。

图1 GWO和CS混合优化算法流程图Fig.1 Flow chart of GWO and CS hybrid optimization algorithm

2 GWO和CS混合优化VMD算法

采用GWO和CS混合优化算法对VMD算法中的分解层数K以及惩罚因子α同时进行寻优，具体步骤如下：

(1) 对GWO和CS混合优化算法进行参数设置，其中，灰狼种群规模为M，最大迭代次数为Tmax，优化参数个数为d。

(2) 设定优化过程中的适应度函数。计算VMD分解的K个模态分量的包络熵E1,E2,…,EK，求得K个模态分量的平均包络熵S，同时定义各个模态包络熵与平均包络熵的差方和为包络熵差异系数B，表达式为：

(11)

式中：Ei为第i个IMF分量的包络熵；pj为a(j)的归一化形式；a(j)为经Hilbert解调后得到的包络信号；N为数据长度。

将各模态分量与原始信号之间的关联程度定义为互相关系数H。

(12)

包络熵差异系数B代表VMD分解模态的差异程度，B值越大表明分解的效果越好；互相关系数H表示分解模态与原始信号的相关性，H值越大表明分解模态与原始信号越相关，包含更多的信号信息。为了实现最终分解模态的差异最大化，同时保留更多的含有原始信号信息的模态分量，故定义包络熵差异互相关系数Q为：

Q=-max(B·H)

(13)

为了获得全局最优值，将包络熵差异互相关系数Q作为适应度值，以其最小值作为寻优目标，利用GWO和CS混合优化算法对VMD的参数组合进行寻优。

(3) 循环迭代直至最大迭代次数后结束计算，得出包络熵差异互相关系数的最小值，其对应的K和α即为VMD最佳分解层数Kopt和惩罚因子αopt。其算法流程见图2。

图2 GWO和CS混合优化VMD算法流程图Fig.2 Flow chart of GWO and CS hybrid optimized VMD

3 仿真信号分析

为了检验优化VMD算法的有效性，构造高频仿真信号x(t)，如式(14)所示。取采样点数4 096，时域波形如图3所示。

设置优化VMD算法的参数M=10，Tmax=20，d=2，α的搜索范围为[200,5 000]，K的搜索范围为[2,10]。

图3 仿真信号波形Fig.3 Simulation signal waveform

(14)

经过优化寻优，得到适应度函数的收敛曲线(见图4)。由图4可知，全局最佳的适应度值即最小包络熵差异互相关系数Q=-1.653 1。对应的VMD最佳参数组合为[1 303,3]。

图4 仿真信号迭代收敛图Fig.4 Iterative convergence diagram of the simulation signal

将优化VMD算法处理结果与常规VMD和EEMD算法进行对比，其时域波形和频谱如图5所示。

从图5可以看出，3种算法均分解出了仿真信号3个主要分量的频率为60 kHz、30 kHz和8 kHz。但是，相对于原始信号分量的波形，常规VMD和EEMD算法处理得到的IMF2和IMF3分量在波形和幅值上均出现了失真；其对应的频谱图中出现了模态混叠，如图5(b)中IMF2的8 kHz成分、IMF3的30 kHz和60 kHz成分以及图5(c)中IMF2的60 kHz成分。而优化VMD算法得到的各IMF的时域波形和频谱成分更接近原始信号分量。为进一步比较3种算法的分解效果，采用常用的反映测量数据偏离真实值程度的均方差J。

(15)

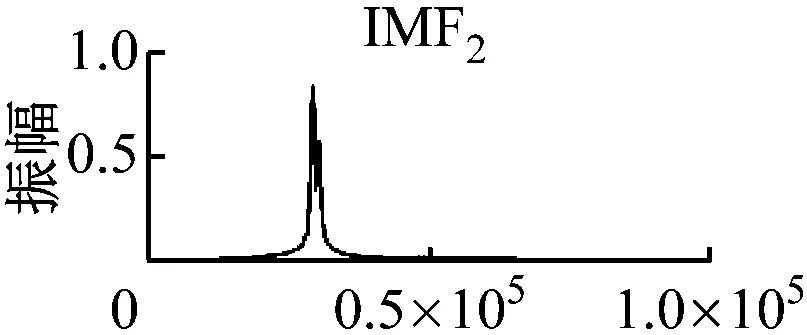
(a) 优化VMD算法

(b) 常规VMD算法

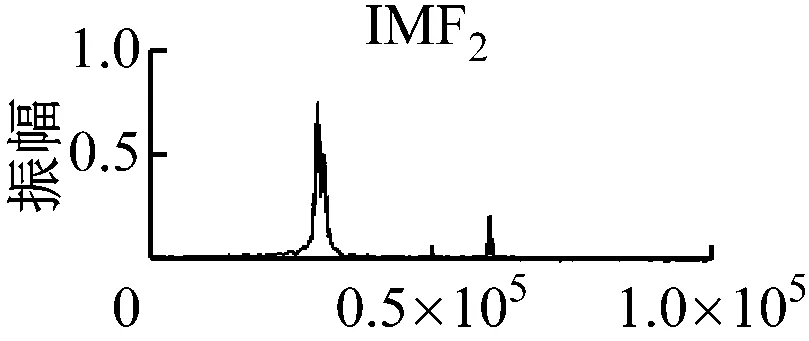
(c) EEMD算法

式中：Ji为分解得到的第i个分量的信号误差；xi(j)为对应分量的原始信号；Ii(j)为分解的模态分量。

Ji越小，表示分解得到的第i个分量与第i个原始信号的偏差越小，分解效果越好，反之，则越差。

上述3种算法处理得到的各分量的均方差如表1所示。由表1可知，优化VMD算法的各均方差均小于常规VMD和EEMD算法，表明优化VMD算法的分解效果最佳。

表1 不同分解算法的均方差

4 试验信号分析

所研究的混流式水轮机空化试验信号来自于一座处于国内领先水平、综合精度<±0.2%的闭式水轮机模型试验台。该试验台配备有水轮机性能测试分析系统，能采集并保存试验数据，实时监测模型水轮机水头和压力的变化，测量并计算单位流量、单位转数等衡量水轮机效率水平的性能参数，了解水轮机空化状态对模型水轮机运行效率的影响。通过调整试验台蓄水箱水位，控制尾水管压力，构造偏离设计工况的试验工况点，按从无到有、从弱到强的顺序改变水轮机的空化状态。水轮机尾水管段为透明有机玻璃，可采用闪频仪记录水轮机流态的变化。为了贴近空化声源，减少信号在过长流道和不同部件的损耗，完整地采集水轮机不同空化状态的声发射信号，分别在模型水轮机导叶拐臂和转轮下环处布置了2套SR-150N声发射传感器，采用PCI-9846H多功能数据采集卡进行信号采集。所分析的声发射信号数据截取于水轮机导叶拐臂上不同空化状态下对应的一段，每段试验数据点数为4 096(见图6)。

分别将3种不同空化状态下的水轮机声发射信号导入以灰狼和布谷鸟组合优化的VMD算法中，得到了不同的分解层数和惩罚因子的最佳参数组合。优化VMD算法分解试验信号的初始参数设置同仿真信号一致。处理后的声发射信号各阶IMF的时域波形及其频谱如图7所示。

(a) 无空化信号

图7 无空化、空化初生和临界空化状态下的IMF及其频谱图Fig.7 IMF and the spectrum under the condition without cavitation, with initial cavitation and with critical cavitation

以临界空化状态为例，优化VMD算法的收敛曲线如图8所示。全局最佳的包络熵差异互相关系数Q=-1.585 3，其对应的分解层数K=8，惩罚因子α=987。其他工况因篇幅限制，不再详述。优化VMD算法参数的寻优结果如表2所示。

不同空化状态的声发射信号分解得到的IMF不同，对应的各频带能量也不同，可作为反映空化程度的特征参数。设xi为分解得到的第i个模态分量IMF，其对应的能量为Fi，则有：

(16)

图8 临界空化状态信号迭代收敛图Fig.8 Iterative convergence diagram of critical cavitation signals

表2 优化VMD算法参数寻优结果

计算各阶IMF能量，保留能量值较大的前5层IMF，其随空化系数变化的关系如图9所示。从图9可以看出，除IMF1外，其他IMF能量值均随空化系数的减小逐渐增大，具有明显的规律性。结合图7中各IMF的频谱图可以看出，IMF1所处的频率段较低，对应的信号成分应为水轮机运行的背景噪声[5]，因此与其他IMF的能量变化规律不同。在尾水真空压力不断降低且尚未低至饱和汽化压力时，空化还未形成，水流流态相对简单稳定，此时采集的信号主要是由水体流动以及水流与水轮机的相互作用形成的。随着压力继续降低至饱和汽化压力时，空泡开始出现，形成气液两相流动，水流流态开始变得复杂，此时为空化初生状态，声发射信号能量较无空化时增大。随着水中空泡数量的急剧增多，溃灭冲击程度加剧，气液两相流的流动更加紊乱，此时采集的声发射信号各频段能量更大。因此，声发射信号分解得到的主要IMF的能量随空化系数变化的关系，可以敏锐地反映混流式水轮机从无空化、空化初生到临界空化的状态变化。

图9 IMF能量与空化系数的关系Fig.9 IMF energy vs. cavitation coefficient

5 结 论

(1) 优化VMD算法以包络熵差异互相关系数为适应度函数，自适应地确定了影响VMD处理效果的最佳分解层数Kopt和惩罚因子αopt，在保证各模态之间差异化最大的同时，又选择了与原始信号相关度最为紧密的模态分量，减少了人为因素造成的主观误差。

(2) 将优化VMD算法用于水轮机空化声发射信号的特征提取，得到位于空化主要特征频率段各阶IMF能量随空化系数的减小不断增大，直接反映了水轮机空化状态加剧，水流更加紊乱的过程，验证了优化VMD算法用于水轮机空化状态识别的有效性。