基于经验小波变换和关联维数的风力机齿轮箱故障诊断
叶柯华,李 春,2,胡 璇
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
由于存在清洁、储量丰富和易于开发等优势,风力发电已经成为当前最重要的可再生能源利用方式之一[1]。随着风力机不断大型化,其内部传动机构日益复杂[2]。此外,因长期处在恶劣非定常风场环境,风力机齿轮箱时刻处于剧烈的交变载荷作用下,同时因长期高速运转、疲劳损伤、加工误差和意外冲击等影响,极易发生各类故障,造成风力机性能下降,严重时将导致报废[3-6]。因此,及时发现和诊断机组故障对保证风力机安全稳定运行具有重要意义。
振动信号凭借易获得、包含信息丰富等优势,成为风力机故障诊断最实用和可靠的分析对象。而风力机齿轮箱通常具有多级结构,其内部复杂的传递路径和各齿轮间不同啮合频率间的调制作用,导致频谱特性复杂,以傅里叶变换为基础的传统方法难以取得较好的分析效果[7]。
蒲子玺等[8]提出了基于平稳小波及峭度准则的变分模态分解方法,可以有效提取强噪声背景下的滚动轴承早期故障信息。Hoseinzadeh等[9]提出一种基于互信息相关系数改进集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法,并用来定量分析轴承故障严重程度。Park等[10]对齿轮箱传动故障信号进行EEMD分解,提取本征模态函数(Intrinsic Mode Function,IMF)的波峰系数和形状系数作为故障特征,结合k值临近算法实现故障的有效分类。Hu等[11]基于集成固有时间尺度分解(Ensemble Intrinsic time-scale decomposition,EITD),采用关联维数作为风力机齿轮箱故障信号特征,提出了一种非平稳故障识别方法。齐咏生等[12]计算了故障信号EEMD分解后各IMF分量的Teager能量算子,结合信号瞬时频率和包络谱建立故障特征向量,通过分析频谱幅值信息对风力机故障类型进行识别。孟宗等[13]采用G-P算法计算轴承在不同状态下振动信号的关联维数,实现故障程度定量分析。Soleimani等[14]同时采用最大Lyapunov指数、近似熵和关联维数,提取强噪声环境下旋转机械的非平稳信号故障特征。该方法由试验数据验证表明,上述特征对变载荷条件下的故障诊断具有较好的鲁棒性。Liu等[15]利用对角谱对故障信号进行分析,再将其构建特征向量用于二叉树支持向量机的故障识别和分类。赵洪山等[16]将最大相关峭度解卷积算法与经验模态分解(EMD)相结合,有效提取风力机轴承早期微弱故障特征。
针对风力机齿轮箱振动信号的非平稳和非线性特征,上述以传统内积变换原理为基础的方法难以取得较好的效果。笔者提出了一种基于经验小波变换(EWT)和关联维数的风力机齿轮箱非线性故障特征提取方法。首先,对故障信号进行EWT分解;然后采用G-P算法计算各IMF分量关联维数,构建非线性故障特征向量;再采用支持向量机(SVM)实现故障的准确诊断,最后采用美国国家可再生能源实验室(NREL)“Gearbox Reliable Collaborative GRC”项目风力机齿轮箱故障数据对所提方法进行验证。
1 经验小波变换
Gilles[17]提出信号处理方法EWT是基于傅里叶谱对信号开展自适应分割的,通过构建小波带通滤波器以提取不同调频调幅分量。
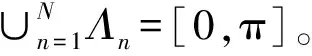
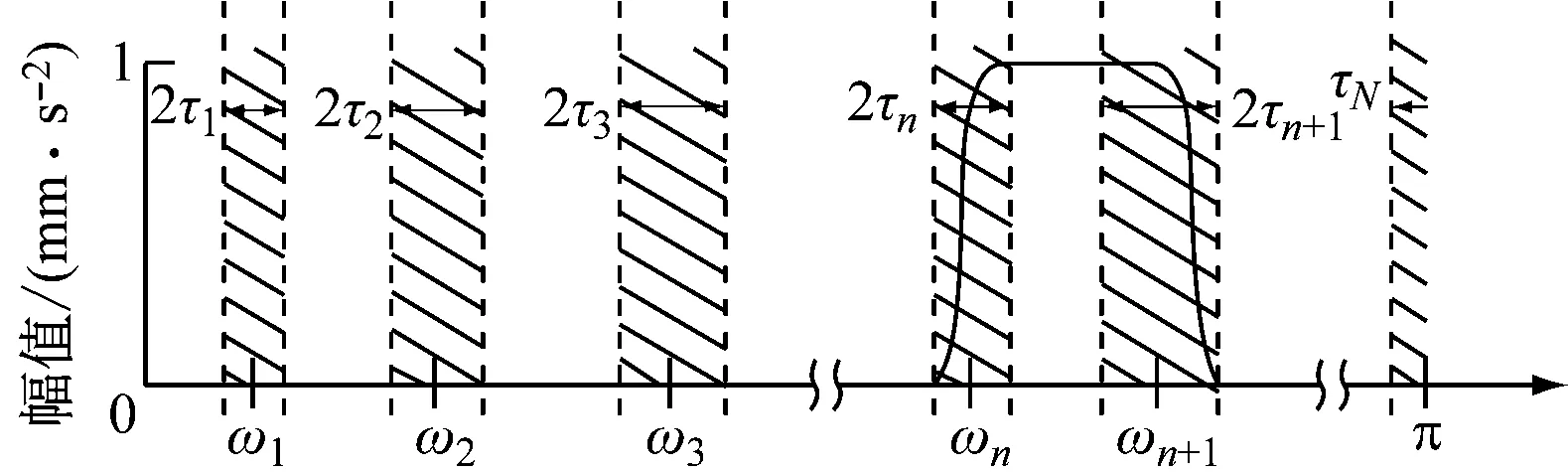
图1 傅里叶谱的分割Fig.1 Segmentation of the Fourier axis
定义相邻频带间存在过渡段,频带宽度为Tn=2τn,其中τn为过渡区宽度,即图1阴影区域。
基于Meyer小波[18]对分割区间Λn构建带通滤波器,则经验小波函数为:
(1)
(2)

β(x)=x4(35-84x+70x2-20x3)
(3)
τn=γωn
(4)
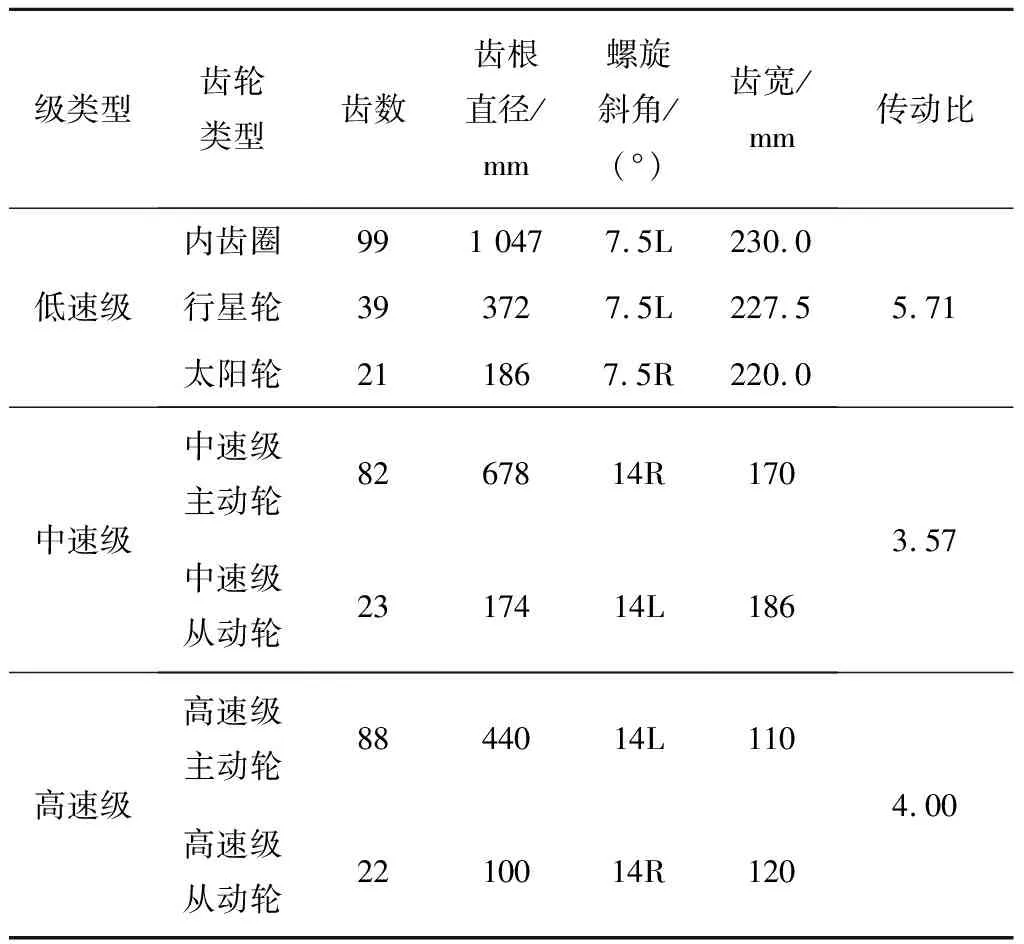
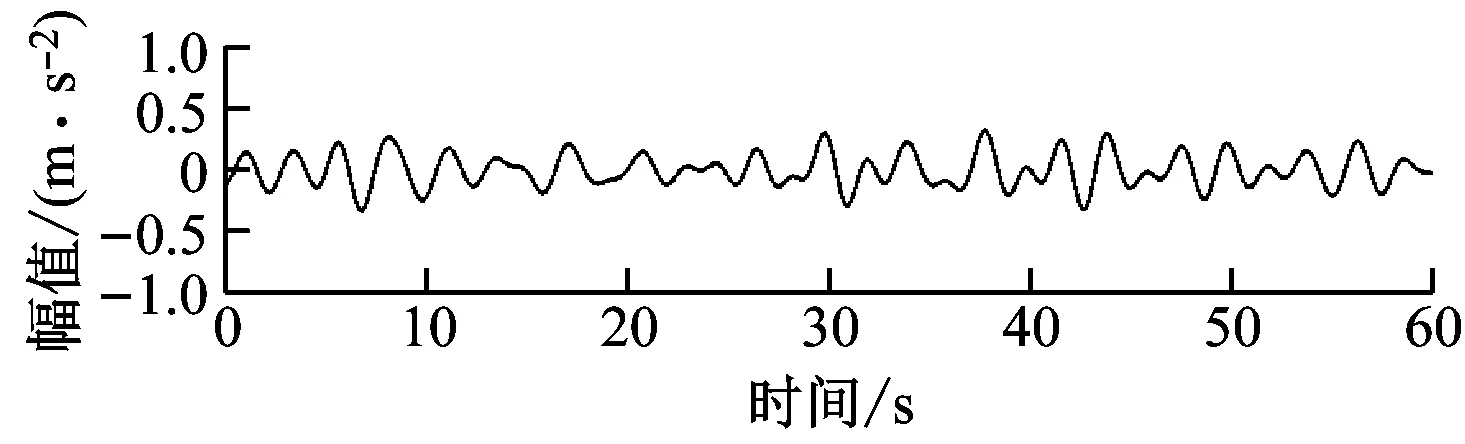
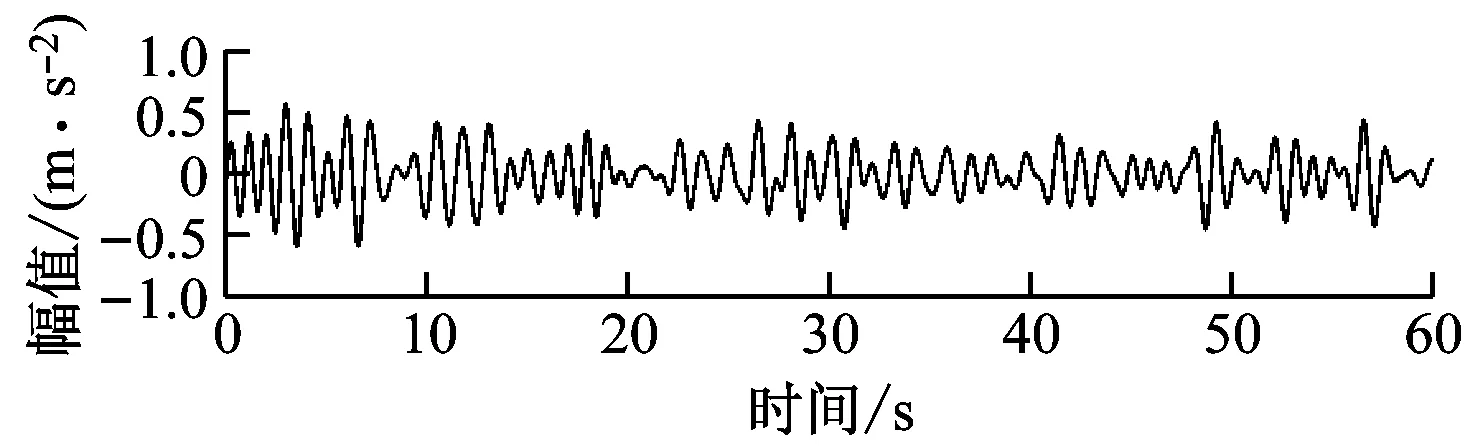
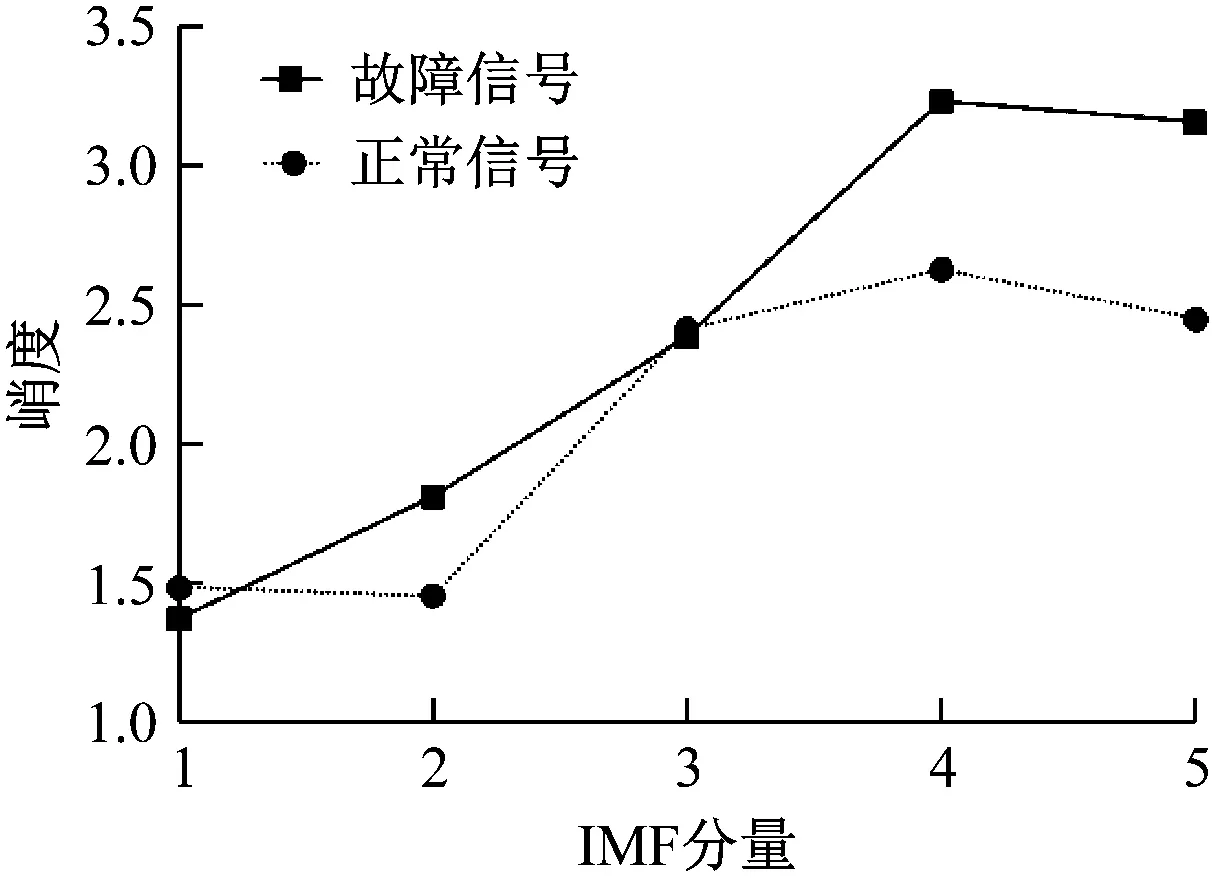
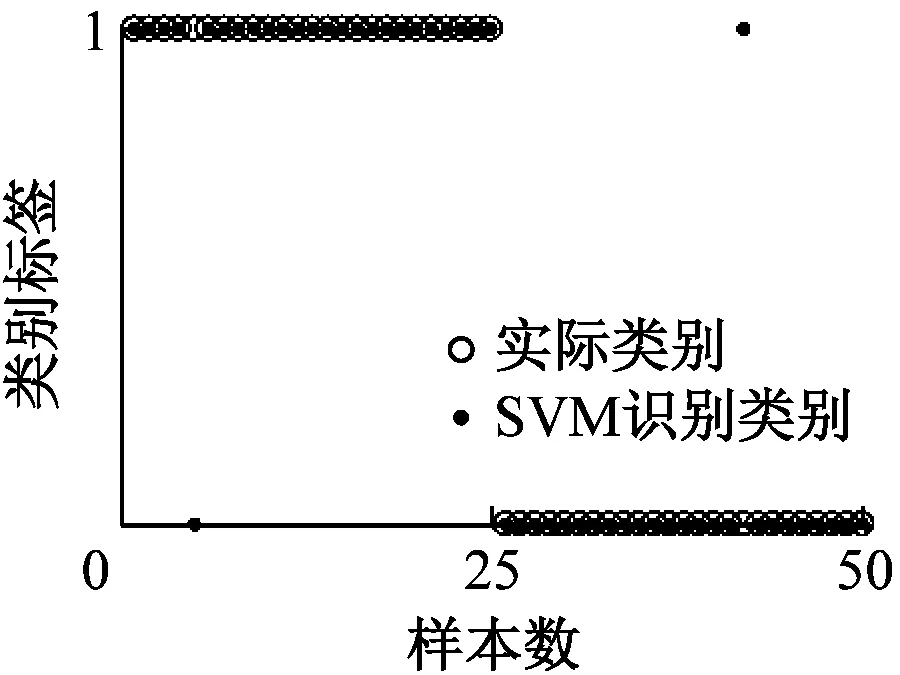
γ (5) 细节系数W(n,t)和近似系数W(0,t)由经验小波函数与信号内积产生: 重构原始信号: (8) 经验模态fk(t)定义为: f0(t)=W(0,t)*φ1(t) (9) fk(t)=W(k,t)*ψk(t) (10) 由于风力机齿轮箱故障信号的非平稳和非线性特征,传统时域频域方法难以提取强噪声背景下的信号故障特征[19]。分形维数作为空间状态中刻画非线性系统行为的重要参数,为表征信号自相似性的量化指标[20-21]。 关联维数作为分形维数的一种,在兼顾计算简便的同时,还能充分反映非线性信号的内在动力学特征[22],故可用来判断风力机齿轮箱振动信号特征参数,进行故障诊断。 基于延时嵌入相空间重构思想,Grassberger等[23]提出的G-P算法是目前计算关联维数采用最广泛的算法。经过多次改进后,其具体计算过程如下。 (1) 相空间重构。 对数据进行采样提取,获得时间序列{xn},相空间重构结果X为: (11) 式中:k为延迟时间;p为嵌入维数;Np为重构相空间中的向量个数,Np=n-(p-1);k为重构相空间的向量个数。 (2) 各向量距离确定。 从Np个向量中选取任意一个数组xi作为参考点,计算剩余Np-1个数组到该点的距离: (12) 重复计算全部数组,得到Np×Np阶矩阵R: (13) (3) 相关函数计算。 对于任意给定的一个数q(q>0),相关函数D(r)定义为: (i≠j) (14) 式中:H为Heaviside函数。 (15) 相关函数表示在p维相空间中2点之间距离小于r的点对在全部点对中的占比,为给定值r的函数。 (4) 关联维数计算。 当r趋于无穷,有关系式: (16) 则关联维数g为: (17) 传统人工神经网络决定节点数难,收敛速度慢。SVM以统计学习理论为基础,具备出色的学习和推广能力,具有良好的小样本分类能力[24]。 设有一组训练集(ai,bi),i=1,2,…,Q,Q为样本数,ai∈Fn为输入数据,其中Fn为样本空间,bi={-1,+1}为输出类别。将输入向量通过非线性变换映射到高维特征空间,转化为近似线性的回归问题。 假设原训练集空间为Fn,由非线性映射函数φ(x)投影至高维空间。设α,β为原空间Fn中的2个向量,根据泛函有关理论,可定义一个满足Mercer定理的核函数k(α,β),因此可得到k(α,β)=Φ(α)Φ(β),Φ为原空间至高维空间映射关系。此时,在不清楚具体映射条件的情况下也可利用高维空间计算内积,使其与高维空间的维数无关,实现非线性向高维线性转变后支持向量回归模型的建立。 因此,SVM算法求解过程最终转化为一个线性约束的凸二次规划问题。未知样本aj决策模型为: (18) 式中:δi为Lagrange乘子;h′为偏置量;sgn()为符号函数。 选取径向核函数作为SVM的核函数,采用遗传算法(Genetic Algorithm,GA)进行全局寻优,确定SVM模型最佳参数,具体流程如图2所示。 图2 基于遗传算法优化的SVM流程图Fig.2 Flowchart of the SVM based on genetic algorithm 针对风力机齿轮箱的振动信号特点,提出一种基于EWT和关联维数的故障诊断方法,诊断过程如下: (1) 选取齿轮箱壳体表面故障和非故障振动加速度信号作为研究对象。 (2) 利用EWT方法对振动信号进行分解,得到多组IMF分量。 (3) 计算各IMF峭度值,选取数值最大的前3个关键分量。 (4) 计算所筛选的IMF关键分量关联维数。 (5) 将所得的关联维数重新排序,首尾相接构成一组特征向量。 (6) 选取部分故障和正常状态下特征向量作为训练数据,通过SVM进行机器学习。 (7) 将余下的特征向量作为测试数据,输入SVM进行状态识别。 本文采用NREL GRC项目采集的风力机齿轮箱故障数据[25]。如图3所示,测试齿轮箱由1级行星轮系和2级定轴轮系构成。表1为齿轮箱结构参数,表中L、R分别表示左旋和右旋。 A-行星架;B-内齿圈;C-行星轮;D-太阳轮;E-中速级主动轮;F-中速级从动轮;G-高速级主动轮;H-高速级从动轮。 齿轮箱风轮额定转速为22.09 r/min,输出轴转速为1 800 r/min。该齿轮箱安装于NREL实验风场内,在运行期间发生油损事故,并逐步演化为多种故障(见表2)。随后NREL将其拆卸,在实验室条件下分别采集其故障和正常状态下的振动加速度数据。箱体上共布置8个传感器(AN1~AN8),具体位置分布如图4所示。 由图4可知,AN8传感器位于高速齿轮轴承处,处在损坏齿轮附近,振动较为强烈,信号所含信息更为丰富,故本文采用AN8传感器采集的信号数据,其采样频率为40 kHz。室内试验齿轮箱处于50%额定功率运转,分别在故障和正常状态下采集10组时长1 min的数据。为便于分析,重新采集采样频率在800 Hz时的信号数据,每间隔50个数据点提取一次,得到故障样本和正常样本各500份。 表1 齿轮箱参数 表2 齿轮箱实际损坏类型 图4 振动传感器位置Fig.4 Location of vibration sensors 图5为AN8传感器采集的齿轮正常和故障状态下的加速度振动信号。从图5可知,振动信号时域波动呈无序且混乱状态,无法直接判断是否发生故障。 (a) 故障状态 (b) 正常状态图5 正常和故障状态下齿轮振动信号时域波形 将故障和正常信号通过EWT分解得到各IMF如图6和图7所示。 (a) IMF1 (b) IMF2 (c) IMF3 (d) IMF4 (e) IMF5图6 故障信号EWT分解结果Fig.6 EWT decomposition result of the fault signal 图8为正常和故障信号各IMF分量峭度值。由图8可知,第3~第5分量峭度较大,故选取第3~第5分量作为分析对象。 分别计算各故障和正常信号EWT分解峭度最大的前3个IMF分量在不同嵌入维数下的关联维数gm,v,h,下标h为信号样本序号,v为IMF分量序号,m为嵌入维数。 将各样本所有IMF分量关联维数构建为高维特征向量Vh。则第h个样本分量的33维特征向量为: (a) IMF1 (b) IMF2 (c) IMF3 (d) IMF4 (e) IMF5图7 正常信号EWT分解结果Fig.7 EWT decomposition result of the normal signal 图8 各IMF分量峭度值Fig.8 Kurtosis of each IMF component (19) 图9为一组故障和正常信号样本IMF3~IMF5分量关联维数的对比。图9中,关联维数随嵌入维数的增加整体呈增大趋势。同一嵌入维数下,故障信号各IMF分量关联维数与正常信号的IMF分量关联维数存在重叠区域,故仅从图像无法准确直观地判断是否发生故障。因此,需要进一步将特征向量输入SVM中进行故障识别。 图9 故障和正常信号样本关联维数与嵌入维数的关系 图10为某一故障和正常信号关联维数的特征向量。故障样本在IMF3下各关联维数大于正常样本,IMF5中则更小。 图10 故障和正常样本关联维数的特征向量 为验证本文故障诊断方法的有效性,计算关键IMF分量均值,并以此构建特征向量,输入SVM作为对比。 训练集样本数分别为100、450、700和950。测试集中样本数均为50个。训练集和测试集中正常样本和故障样本各占50%。 采用遗传算法对SVM优化核参数和惩罚系数后,不同训练集样本数下关联维数和均值特征向量测试集的识别结果如图11和图12所示。其中,故障样本标识为“1”,正常样本标识为“0”。图中圆圈标记为样本实际结果,圆点标记为SVM识别结果。 由图11可知,当训练样本数为100时,关联维数特征集有48个样本能准确识别。训练样本数增加至450后,所有样本均被准确分类。 由图12可知,均值特征集SVM样本识别准确率明显低于关联维数特征集。当训练样本数为100时,7个正常样本未被正确识别。当训练样本数为950时,仍有4个样本出现分类错误。 表3为测试集样本数为50时,不同训练集样本数下的SVM故障识别准确率。从表3可知,关联维数特征集故障诊断样本的识别准确率明显高于均值特征集。当训练样本数为100时,关联维数特征集故障识别率可达98%,因此所提方法可满足小样本数故障诊断要求。 (a) 100个训练样本 (a) 100个训练样本 表3 不同样本数诊断精度 (1) 齿轮箱振动信号的关联维数与嵌入维数呈正相关;EWT分解的样本各IMF分量因包含能量逐渐增加,故关联维数大小总体也逐渐增加;且故障状态关联维数较正常状态关联维数更大。 (2) 对经过EWT分解后的IMF分量进行关联维数计算,齿轮工作状态不同,其振动信号的关联维数不同,虽然能有效提取齿轮箱信号故障信息,但仍无法准确判断故障类型。 (3) 与以IMF分量均值作为SVM输入参数相比,将基于EWT和关联维数所构建的特征向量输入SVM得到的故障识别准确率更高,更稳定,准确率高达100%,可有效实现风力机齿轮箱的故障诊断。
2 关联维数
3 支持向量机

4 基于EWT和关联维数的故障诊断方法
5 应用与分析
5.1 实例数据分析


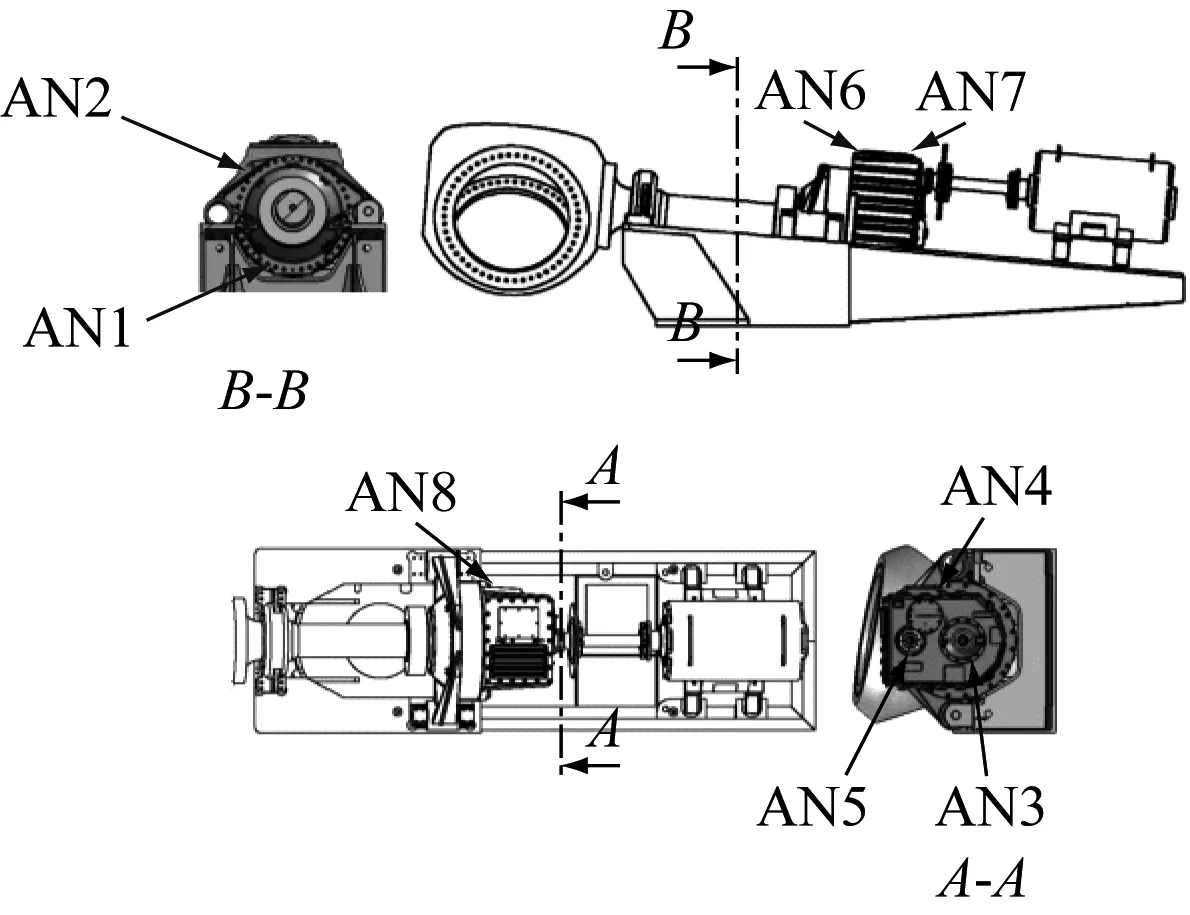
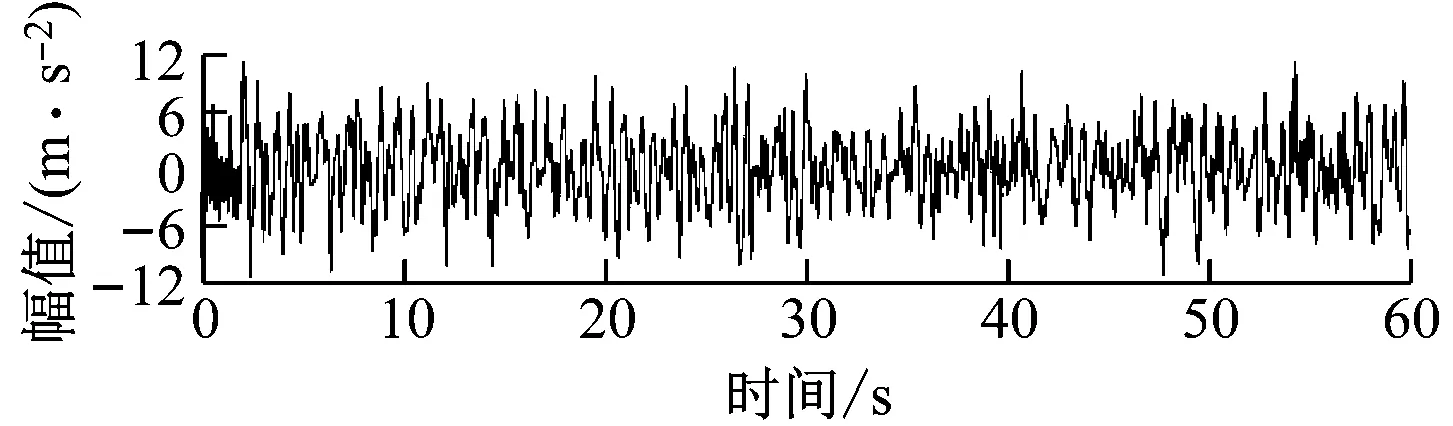


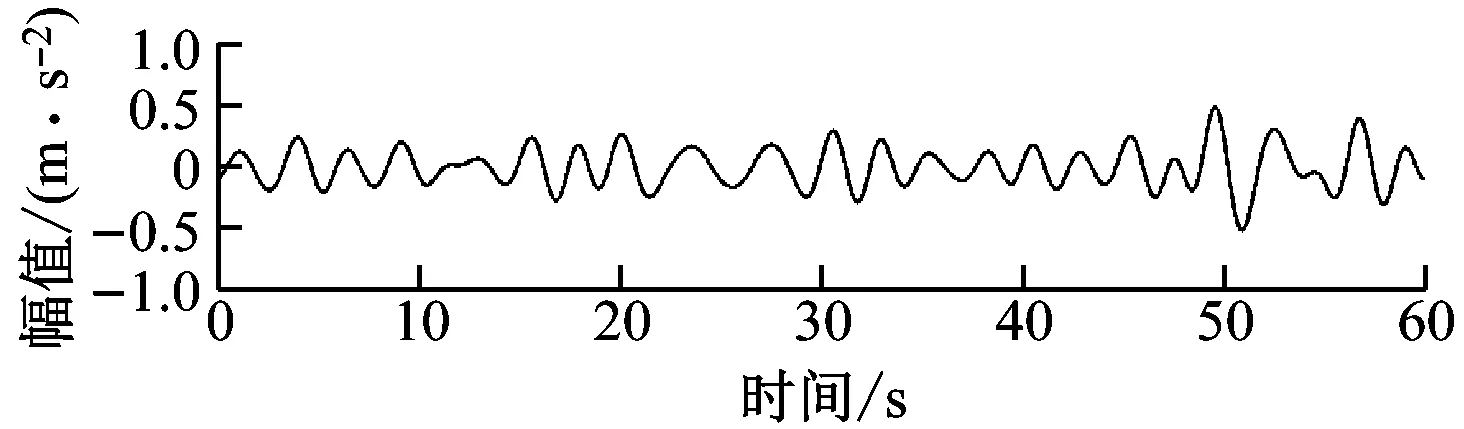
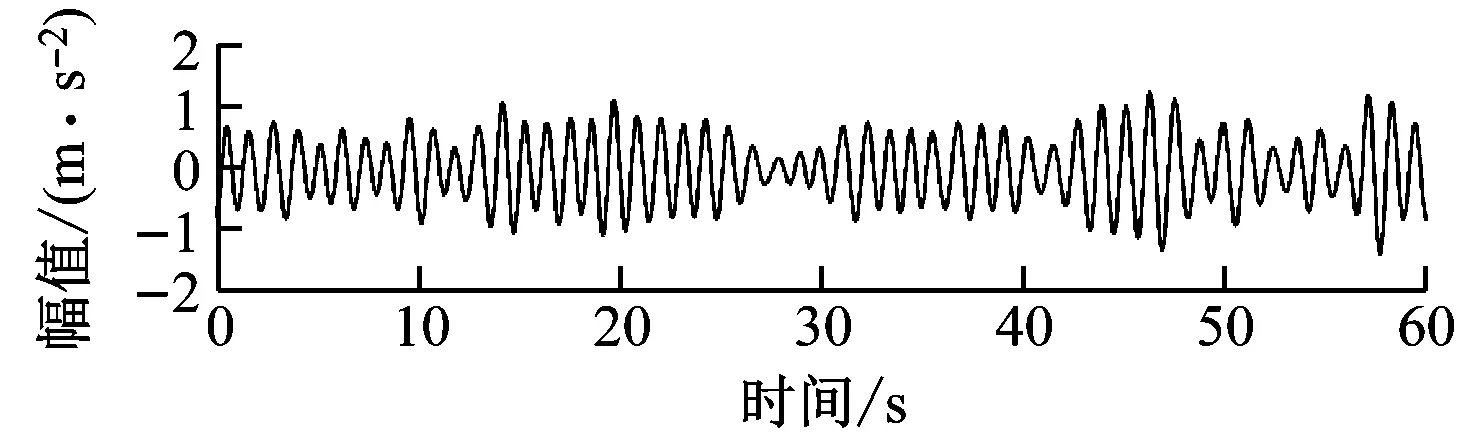


5.2 特征参数提取





5.3 模式识别与分类


6 结 论

