环境风影响下直接空冷阵列入口空气流量特性实验研究

孔新博，罗智凌，冯鹏远, 李 泓，周振华，张金祥

(1．华北电力大学 控制与计算机工程学院，北京 102206；2.中国科学院国家空间中心，北京 102206;3．国电电力大连庄河发电有限责任公司，辽宁大连 116000)

直接空冷技术利用空气作为冷却工质，通过轴流风机群强化空气流动以达到冷却乏汽和降低机组背压的目的，且直接空冷机组的耗水量仅为传统湿冷机组的20%[1-5]，其由于具有显著的节水效果，在我国富煤缺水的北方地区得到大规模应用。2016年，国家能源局确定的20个太阳能光热发电示范项目名单[6]中，有19个分布在西北缺水地区，均采用直接空冷机组。然而，采用空气作为冷却介质会使凝汽器的换热效率降低，导致背压升高，机组出力降低。此外，与传统湿冷机组凝汽器相比，空冷凝汽器的核心部件轴流风机群耗电量更大。直接空冷阵列轴流风机入口空气体积流量(简称风机体积流量)是影响凝汽器效率的关键因素，合理调节风机运行方式是空冷阵列节能优化的重要工作。由于凝汽器布置在露天环境中，环境风对风机体积流量影响显著，因此，研究直接空冷阵列在环境风影响下的运行特性具有重要意义。

Conradie等[7-8]的研究结果表明，在环境风影响下空冷阵列外围风机性能恶化是引起凝汽器换热效果差的主要原因。Hotchkiss等[9]发现横向环境风会使风机的工作效率降低。黄鹤等[10]对330 MW直接空冷凝汽器进行数值仿真，结果表明环境风是导致风机体积流量和凝汽器出口温度不均的主要原因。江泽铭等[11]研究了不同风况对300 MW直接空冷凝汽器换热性能的影响，发现空冷阵列迎风面第1行受环境风影响最大。王维英等[12]以宁夏某电厂350 MW直接空冷机组为例，研究不同风况对直接空冷机组背压和负荷的影响。杨立军等[13]通过实验发现风机并联运行时的空气体积流量远低于风机独立运行时的空气体积流量。张辉等[14]提出采用位置系数来衡量风机效率，实验发现无风环境下外围风机位置系数较小。目前，对于环境风影响下风机入口空气流量特性的分析仍以数值模拟为依据，缺少实验数据支撑。

笔者依托搭建在露天环境下的空冷阵列实验平台，在环境风扰动下测量每台风机的体积流量，分析空冷阵列风机体积流量与风况(即风速、风向)的关系；利用风机体积流量实际值计算不同风况下凝汽器背压，对传统背压模型进行修正，对空冷阵列转速控制器的设计提出了建议。

1 直接空冷系统和凝汽器模型

1.1 直接空冷系统

直接空冷系统结构见图1，包括空冷阵列平台、控制系统、调速系统和测量系统4部分，直接空冷系统的设备参数见表1。

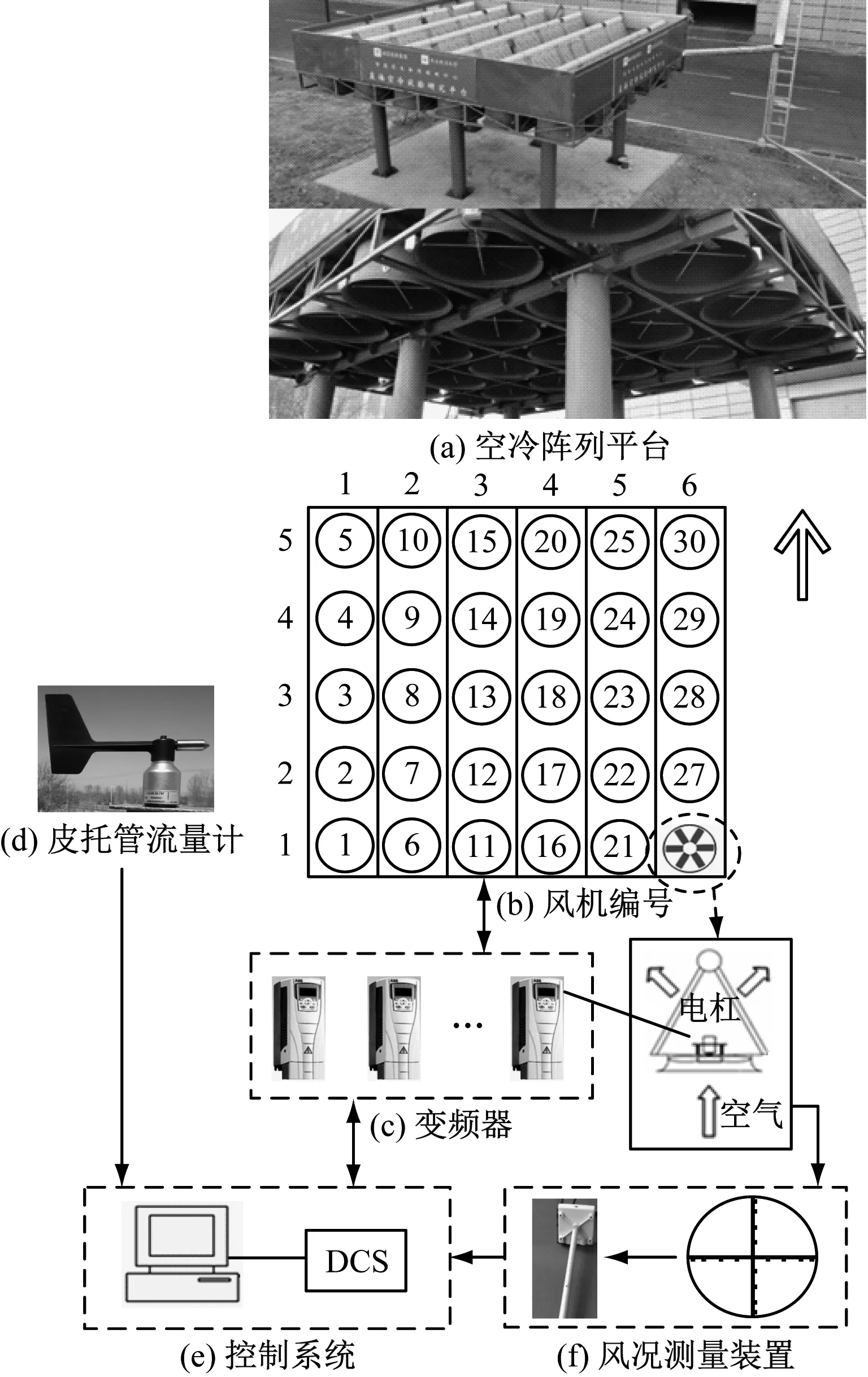
图1 直接空冷系统结构Fig.1 Structure of the direct air-cooling system

空冷阵列平台仿照国内某330 MW直接空冷机组的空冷阵列，以10∶1的比例建设而成，实验平台周围空旷且各方向风温一致。每个空冷单元包括1台风机、1对模拟翅片管和1台变频器。控制系统采用分散控制系统(DCS)，通过DCS监测风况和风机体积流量，控制风机转速。风机由交流电机驱动，调速方式为变频调速。30台变频器独立驱动30台交流电机，实现交流电机转速的单独控制。变频器功率为3 kW，与风机转速对应。在实验平台西南侧安装机械式风速风向仪，与空冷阵列平台同高，并保证周围无遮挡。风向传感器输出角度信号，角度为水平风来向。

采用皮托管流量计测量风机体积流量，每个空冷单元安装2根皮托管流量计，每根有8个风速测点。根据等面积环原理[14]布置测点，取16个测点的平均值作为第i行、第j列风机的体积流量qV,ij,c。

表1 直接空冷系统参数

(1)

式中：Vn为每个测点附近的瞬时风速；A为截面积。

1.2 冷端系统传统模型

管内蒸汽冷凝放热量为Q1：

Q1=qm,c(hc-cp,wTh)

(2)

式中：qm,c为排汽质量流量；hc为排放蒸汽焓；cp,w为水的比定压热容；Th为冷凝水温度。

管外空气吸收热量Q2为：

Q2=ρqVcp,a(Ta2-Ta1)

(3)

式中：ρ为空气密度；qV为风机体积流量；cp,a为空气比定压热容；Ta2和Ta1分别为冷却风出口、进口温度。

换热过程可以通过传热效率和传热单元数来描述，即：

(4)

(5)

式中：ε为传热效率；NTU为传热单元数；K为表面传热系数；AF为散热器换热面积。

根据能量守恒定律，管内蒸汽冷凝放热量Q1与管外空气吸收热量Q2相等。

联立式(1)～式(5)，冷凝水温度Th为：

(6)

根据风机的相似定律，满足相似条件的风机体积流量之比等于风机直径之比的3次方与转速之比的乘积。因此，可以利用实验平台风机的体积流量计算风机体积流量实际值，进而得到凝汽器背压。

根据经验公式，背压pb=[(Th+100)/57.66]7.46×9.8×10-3，该公式的计算精度足以满足工程需要。背压会影响排汽焓降，进而改变发电功率。此外，背压会对凝结水的温度产生影响，而末级排汽压力会随凝结水温度的变化而变化，从而改变有效排汽焓降，影响发电功率。

2 实验数据处理

2.1 单台风机体积流量基准值的测量

(7)

式中：qV,ij,m为风机体积流量实验值；qV,d为风机体积流量设计值。

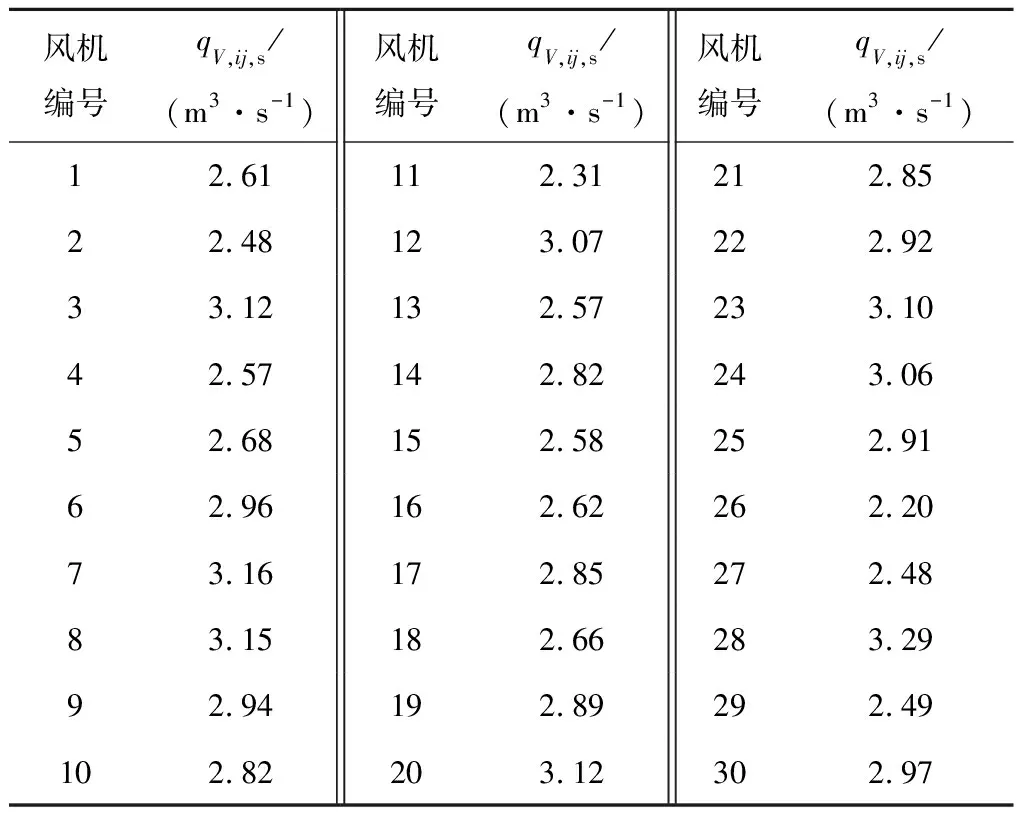
表2 风机独立运行时体积流量基准值

2.2 平均风向

采用单位矢量平均法[15]计算平均风向，其原理是统计各时刻下风向标度在坐标轴上的投影，计算累计风向标度投影的平均值，再通过反正切的方式还原平均风向。其中,设置正北风向为0°,沿顺时针增大。

(8)

图2 平均风向的变化Fig.2 Average variation of wind direction

2.3 风速

卡尔曼滤波算法是一种最优状态估计的方法，通过在模型的状态空间方程中增加测量噪声和过程噪声2个变量，使最优状态估计的协方差最小。其中，最优状态估计值通过模型预测值与测量值加权求和得到，而权重即为卡尔曼增益。模型预测值包含预测误差，测量值包含测量误差，通过卡尔曼增益可将二者融合，取概率最大的数值作为最优状态估计值。

式(9)为卡尔曼滤波算法的5个基本方程，分别为状态一步预测方程、一步预测误差协方差方程、卡尔曼增益方程、状态估计方程和滤波误差协方差方程。

(9)

式中：X(t,t-1)为用t-1时刻状态量预测得到的t时刻状态量；φ(t,t-1)为t时刻的状态转移矩阵；X(t)为t时刻最优状态估计值；P(t,t-1)为t时刻预测误差的协方差矩阵；P(t,t)为t时刻滤波误差的协方差矩阵；K(t)为t时刻卡尔曼增益；H(t)为t时刻测量系统参数矩阵；Y(t)为t时刻风速测量值矩阵；Q(t)为t时刻过程噪声的协方差矩阵；R(t)为t时刻测量噪声的协方差矩阵;I为单位矩阵。

受实验平台环境因素的限制，风速的测量范围为0～9 m/s。对1 800个风速实验数据进行处理，结果如图3所示。

图3 经卡尔曼滤波后风速与风速测量值的对比Fig.3 Comparison of wind speed before and after Kalman filtering

3 结果与分析

3.1 流量特性

为分析风向变化时风机体积流量的分布特性，在风向变化剧烈的天气进行实验。实验过程中所有风机以30 Hz频率运行，环境温度为20 ℃，各方向风温均保持不变。

从直接空冷系统的历史数据库中选取具有代表性的60 s风向持续变化的数据，并选取其中5个时间段(T1～T5)进行分析，如图4所示。分别计算每个时间段的平均风速和风向，以及每台风机的平均体积流量，在不同时间段内风机体积流量的分布见图5。其中，T1时间段内平均风速为3.3 m/s，平均风向为北偏西10°；T2时间段内平均风速为2.1 m/s，平均风向为西偏北4°；T3时间段内平均风速为2.7 m/s，平均风向为南偏西27°；T4时间段内平均风速为1.8 m/s，平均风向为南偏东26°；T5时间段内平均风速为2.1 m/s，平均风向为西偏南6°。由图5可知，环境风下迎风侧第1列(或行)为流量低谷区，且流量低谷区随风向的变化而转移，基本无时间延迟。

按列求和得到各列风机体积流量，其分布见图6。风机总体积流量为97.2 m3/s，迎风侧第1列的体积流量最小(11.6 m3/s)，占总体积流量的11.9%，第3列的体积流量最大(18.0 m3/s)，占总体积流量的18.5%。除迎风侧第1列风机外，其他区域各列风机的体积流量分布较均匀，这与文献[11]和文献[13]的结论相同。

图4 风速和风向随时间的变化Fig.4 Variations of wind speed and direction with time

(a) T1

图6 西偏北20°风向下各列风机体积流量的分布

进一步计算在风速为2 m/s时不同风向下风机平均体积流量，结果见表3。由表3可知，在不同风向下风机平均体积流量相差不大。

3.2 不同风速下风机的流量特性

在风力较强的天气下开展实验，所有风机以30 Hz的频率持续运行，风向见图2。通过计算可知，风向在280°～330°的数据所占比例为76.3%，可以认为该时间段风向基本稳定，选取风速分别为2 m/s、4 m/s、6 m/s和8 m/s的风机体积流量，并计算各列风机平均体积流量，其与风速的关系见图7。从图7可以看出，受环境风影响，第1列风机的平均

表3 不同风向下风机平均体积流量

图7 不同风速下各列风机平均体积流量的分布

体积流量显著低于无风情况，且风速越大，体积流量越小。进一步对各列风机体积流量的动态特性进行分析，各列风机体积流量与风速之间的关系见图8。

从图8可以看出，迎风侧第1列(即第1列)风机的体积流量在300～900 s内波动剧烈，在该时间段内风速由1.5 m/s增大至6.3 m/s，第1列风机的体积流量由10 m3/s减小至7.9 m3/s；在800～1 200 s内风速减小至1.9 m/s，因此体积流量明显提升。

(a) 第1列

(d) 第4列

各列风机体积流量标准差Rstd及其与风速之间的相关系数Rcor分别为：

(10)

(11)

式中：qV,ave为各列风机体积流量算术平均值；V为风速；D(qV)、D(V)分别为各列风机体积流量和风速的方差。

相关系数表征风机体积流量受风速的影响程度，相关系数的绝对值越大，表明风机体积流量对风速的影响越大。相关系数大于0时，风机体积流量随风速的增大而增大；相关系数不大于0时，风机体积流量随风速的增大而减小，具体计算结果见表4。

从表4可以看出，在风向基本不变、风速连续变化的环境风影响下迎风侧第1列(即第1列)风机的体积流量标准差最大，且远大于其他列；迎风侧第2列(即第2列)和背风侧第1列(即第6列)风机的体积流量有明显波动，中间3列风机体积流量基本稳定；迎风侧第1列风机的体积流量与风速呈负相关，迎风侧第2列和第3列(即第3列)以及背风侧第1列风机的体积流量与风速呈正相关，其他2列风机体积流量与风速基本无关。迎风侧第1列风机的体积流量与风速的相关系数为负，随风速快速变化，基本无时滞。风速波动是引起迎风侧第1列风机体积流量波动的主要原因。图9给出了风机体积流量标准差与风速的关系曲线。

表4 各列风机体积流量标准差及其与风速的相关系数

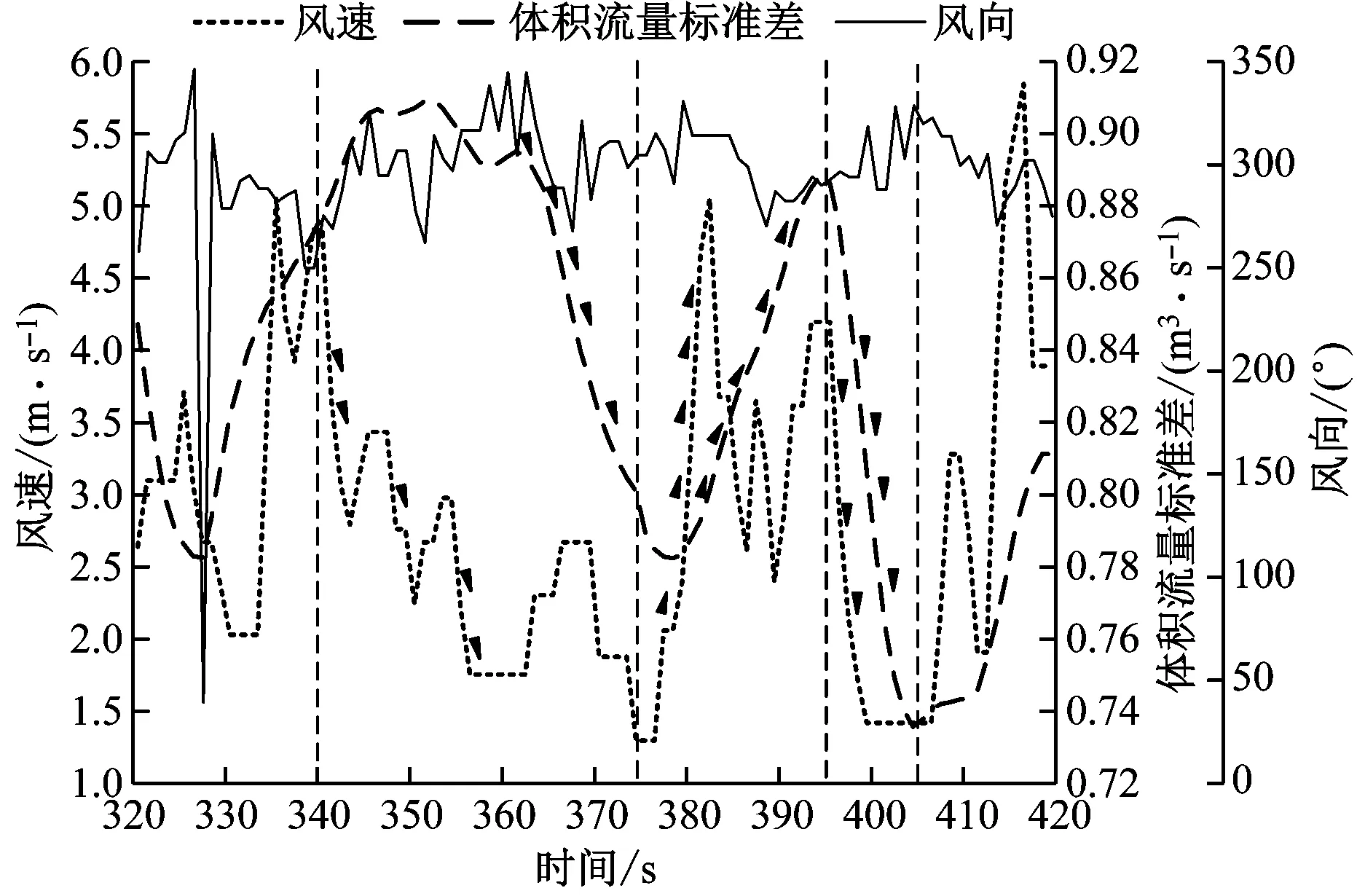
图9 风机体积流量标准差与风速的关系

3.3 环境风对凝汽器背压的影响

风机体积流量受到集群效应和环境风影响，因此根据实验数据估计机组的风机体积流量，建立了背压模型并进行验证。验证对象为330 MW直接空冷机组，设计风机体积流量为518 m3/s，风机额定功率为110 kW，风机直径为9.144 m，风机额定频率为50 Hz，总散热面积为847 432 m2，设计背压为15 kPa。选取4组实验数据，分别计算机组背压差，并将其与背压实际值进行对比，模型验证结果见表5。从表5可以看出，相比于传统模型，本文模型背压计算值的相对误差较小，精确度提升了2%～5%。这是由于在风机实际运行中存在风机集群效应以及环境风对风机总体积流量的影响，导致风机效率降低。

为分析不同风速对凝汽器背压的影响，选取6组不同风况的实验数据，所有风机以50 Hz频率运行。根据风机相似定律和本文所建背压模型计算凝汽器背压，见表6和表7，其中工况1～工况3分别表示环境温度为10 ℃、20 ℃和30 ℃，工况4～工况6分别表示负荷率为50%、75%和100%。

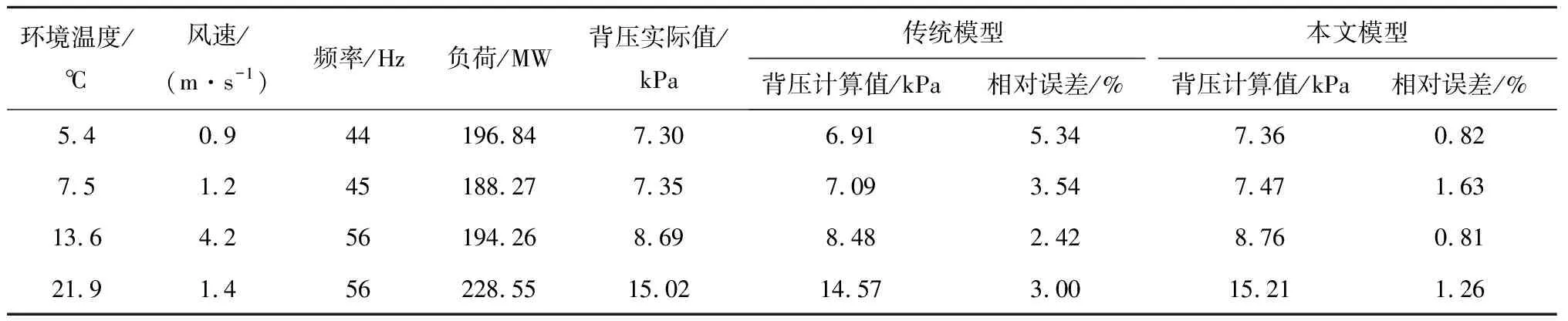
表5 背压模型验证

表6 额定负荷下凝汽器背压

表7 20 ℃环境温度下凝汽器背压

将实验数据中有风和无风时的背压进行对比，发现有风时凝汽器背压较大；当风速基本不变时，不同风向下机组背压差异不大；当风向基本不变时，风速越大，凝汽器内冷凝温度和背压越高，在额定负荷下风速从2 m/s增大至8 m/s，其背压较无风时的增幅约为0.5 kPa；当负荷一定时，环境温度从10 ℃升高至30 ℃，其背压较无风时的增幅约从0.5 kPa提高到1 kPa；当环境温度相同时，机组负荷率从50%提高至100%，其背压较无风时的增幅约从0.2 kPa提高到0.7 kPa，因此在夏季机组以高负荷运行时，需要充分考虑环境风的影响。

3.4 空冷风机控制优化建议

风机体积流量直接影响凝汽器的换热效果，环境风的存在造成迎风侧第1列风机体积流量显著减小，也使空冷阵列体积流量分布的不均匀性加剧。为削弱环境风对空冷阵列产生的不良影响，对空冷阵列转速控制器的设计提出以下建议：

(1) 在空冷风机底部安装空气流量计，实时监测风机体积流量，同时将风机体积流量和凝汽器背压作为反馈参数引入控制回路。

(2) 采用分区控制，即针对风机体积流量高且稳定的空冷阵列区域，提高风机转速；针对风机体积流量低且波动大的区域，降低风机转速。

(3) 空冷阵列长期处于稳定的环境风向时，将迎风侧第1列风机作为区域Ⅰ，其他风机作为区域Ⅱ；环境风向变化频繁时，考虑到实际控制器中不宜频繁切换控制模型，建议将体积流量波动较大的最外圈风机作为区域Ⅰ，体积流量较稳定的内部风机作为区域Ⅱ。

4 结 论

(1) 空冷阵列在环境风的持续影响下，迎风侧第1行(列)风机体积流量显著减小，而背风侧风机体积流量较大；流量低谷区随风向快速变化，无迟延；不同风向下风机平均体积流量差别不大，风向仅影响流量低谷区的位置。

(2) 迎风侧第1列风机的体积流量与风速呈负比例系数关系，风速变化是引起迎风侧第1列风机体积流量波动的主要原因。

(3) 实际运行时，在环境风影响下凝汽器背压高于无风时的背压。背压随风速的增大而增大，且环境温度和运行负荷较高时环境风的影响更为显著。