小学数学“数与代数”中数学模型的建构

■江苏省徐州市睢宁县桃园镇魏圩小学 袁 媛

一、基于数学问题情境是数学模型建构的基础

小学学生处于形象思维向抽象思维的过渡时期，基于数学生活的问题情境，特别是通过一些童话故事带入的情境，可以激发学生学习的兴趣。如教师在指导学生学习“小数的基本意义与性质”的时候，通过一则童话故事来导入教学，能够激发学生的学习兴趣。在运用故事导入的过程中，不是为了讲故事而讲故事，而是要让故事内容与学生的学习内容紧密地联系起来，让故事情境服务于教学情境。通过故事激发学生的学习兴趣，勾连起学生的认知经验，为数学建模提供帮助。此外，教师创设的故事内容要短小，故事要精彩，要与学生的生活、心理、认知联系起来，不能在教学过程中占用太多的时间。教师还要具有一定的创编故事、讲述故事能力，通过教师的“讲”，能够激发起学生学习的兴趣，为数学模型建构提供基础。

二、经历“数与代数”抽象、运算与建模的过程

学生在数学模型建构的过程中，首先要经历思维的参与，只有产生思维活动，才能从数学生活中认识数学关系，借助数学关系进行运算，最后才能达到建模的过程。其次，教师要基于学生生活提出数学问题，从学生能够理解的数学生活出发开展教学。最后，教师要引导在具体建模中完成对知识的再次回顾，实现学习支架的搭建。如在“正比例和反比例”的学习中，教师就可以设置这样的学习环节。

教师出示数学题：学校阳光食堂100kg面粉可以做出125kg馒头，照此计算，要做出200kg馒头，需要多少千克的面粉？从题中，我们可以看出“面粉”与“馒头”是两个基本的量；二者之间的关系通过“出饼率”表现。这道题目是从学生司空见惯的日常生活中提取的，学生对于其中的关系能够轻易理解。但是要想走向数学建模，就需要运用数学符号来表达其中的数学问题，发现其中的数量关系和变化规律。在教学当中，教师需要组织学生通过对题目当中数量关系的观察，对变化关系的概括，分析完成模型抽象，得到模型，这是学习的第一个环节。

在数量分析的基础上，我们不难发现，需要把问题聚焦在“出饼率”上。它直接关系着面粉与馒头两者数量之间的关系。由此可见，我们可以得到关系是馒头量=面粉量×出饼率。这道题目并不是要得到这两道题的准确答案，而是让学生建立起其中的数学思维。在本道题中，馒头量=面粉量×出饼率。面粉与馒头是变量，但它的“出饼率”固定的。因此，馒头和面粉成正比例关系。如果通过列式计算，则为：125÷100=1.25；200÷1.25=160千克。当然，这道题目并不是为了考察学生的运算过程，而是让学生经历思维的活动过程，唤醒学生运用比例知识解决问题。因此，教师要引导学生进行具体的分析，得出如下结论：

本道题目中，面粉和馒头是变量，但是“出饼率”是不变量。列方程的方式去解，则设：要做出200kg馒头，需要x千克面粉。

馒头量=面粉量×出饼率

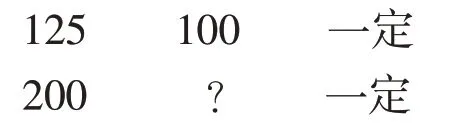
因此，面粉和馒头成正比例，通过列方程不难得出：

解：设要做出200千克的馒头需要x千克的面粉。

125：100=200：x

在教学中，教师通过这种式让学生思考，就是引导学生对数学模型建构过程进行思考。在第一次解题过程中，学生大多会基于两种数量关系进行直接计算，其思维没有经过整合，缺少了模型建构的过程；以上比例的方式则是让学生通过思维的发生，重新建立了思维模型。在这道题目的学习过程中，第一次是通过数学的方式解决问题；第二次是通过数学思维建模的方式解决问题。我们不难发现第二个方法更好，因为当学生建立了这样的数量关系后，对于其他的题目就能够熟能生巧，举一反三。这样的学习过程是进步的过程，在这种模型当中，一是数量关系的变与不变，是内容层面的；第二是方法层面的，即数学模型的建构与运用。

三、建构模型支架，运用数学模型学习

建模的过程就是“数学化”的过程。教师在教学中要时刻关注“数学化”的时间，找准“数学化”的节点，让学生运用数学模型学习，回到数学生活中完成知识的建模。如在“用字母表示数”的教学中，在学生建构起了用“字母”表示数的数学模型后，教师需要及时引导学生发现“用字母表示数”背后隐藏的知识结构，建立起符号思维，搭建起符号模型，让学生的思维品质得到发展。学生通过学习，已经初步具备了可以用字母表示任意一个数字的能力，在具体的学习运用，教师需要抽丝剥茧，让学生抵达知识的核心，建构起数学模型。

教师在研究完“x”在字母与数字之间的关系后，可继续让学生看一看教师的年龄如何表示，如果用“x”来表示，这里的“x”能不能“表示任意的数”，让学生经历思维建构的过程。通过这个环节，教师梦将让“字母表示数”的知识与学生的生活联系起来。有的学生认为这里的“x”大约能表示“25～35”之间的数字。教师顺势引出，“x”表示任意的数是“有范围”的；接着出示家中的小狗，让学生继续猜小狗的年龄。在这个环节中，让学生建构起“同一个问题中，不能用相同的字母表示不同的量”的概念。接着教师出示小狗比自己小32岁，让学生运用算式来表示，引导学生说出“x-32”，然后让学生说一说其中的数量关系。“x-32”是运算过程还是运算结果。最后，教师继续指出：“老师的年龄和小狗的年龄都会变化，如果继续用数量关系表示，其中有变量与不变量。”教师可让学生说一说其中的关系。经过这样的学习过程，学生在用“字母表示数”的数学模型运用的过程中就能够联系生活，联系知识概念与方法，实现知识的内化。

总之，数与代数的学习分布在教材的不同学段，包含着不同的数学模型。在教学中，从教师角度，教师需要从“数”的角度去理解，从生活的角度去设计，从思维的角度构建学习支架，帮助学生建立起数学模型，在具体的数学活动中运行数学模型，实现知识的迁移与内化；从学生角度，学生需要在具体的情境中理解“数与代数”，在真实的思维活动中获得“数感”的发展，感受模型的不同表征。此外，“数与代数”还需要与学生的数学生活、现实生活结合起来，需要与数学知识的整体建构结合，需要与学习发展的整体脉络结合。教师只有丰富问题情景、强调教学多样、学会把握数学关系、发展符号意识、探究数学规律，才能实现小学学生数学素养的全面发展。