新型电力营销智慧管控平台的设计与研究
袁轶,施沩,梁甜甜,季铮铮
(1.国网江苏省电力有限公司南通供电分公司,江苏 南通 226001;2.江苏电力信息技术有限公司,江苏 南京 210024)
0 引 言
电力智慧营销和管理中,数据的隐私性一直是电力营销管理领域的一个研究重点问题。文献[1]提出了一种基于全同态加密的智能电网数据隐私保护方案,首先分析了目前智能电表的用户隐私保护的两个阶段,根据现有的智能电网数据交换方案,设计出一个全同态数据隐私保护系统,虽然能够提高一定的数据隐私性,但是其加密的运算范围只限于整数,仍然存在被破解的可能性。文献[2]针对光伏电站逆变器的故障诊断问题。首先分析了逆变器的故障类型,将故障诊断问题转化成多分类问题;然后采用合成少数类通过采样技术人工生成数据样本,避免数据不平衡问题;最后,由实时监测数据提取特征向量,通过稀疏贝叶斯极限学习机训练模型,根据概率分布实现逆变器的故障多分类。
基于以上内容,本文设计了一个新型电网营销管理平台,能够提高数据加密的可靠性和光伏电站的监测和管理能力。
1 电力营销智慧管控平台
本文设计的电网营销管控平台的架构如图1所示。该平台主要是对电网营销数据进行管控,可以分为5层:数据来源层、采集层、存储层、处理层和分析层[3]。
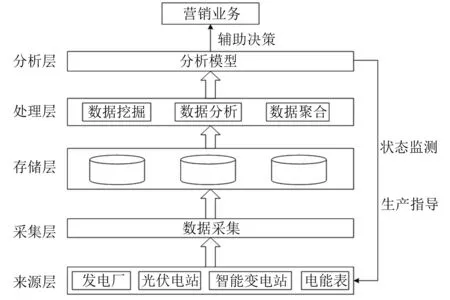
图1 电网营销管控平台架构
数据来源层主要为一些发电厂,像光伏电站一类的清洁能源发电站,智能变电站和智能电表。数据的类型主要为电量数据、营销数据和电站状态数据。
数据采集层主要为一些传感器,建立传感器物联网实现统一管理,通过设置采集频率来实现定期采集,同时为了防止数据不完整,补充设置采集时间[4]。
数据存储层主要负责数据的存储,本文采用云存储技术来对采集的数据进行存储,云存储技术能够利用小容量的存储设备实现大容量数据的存储,能够满足系统的需求[5]。
数据的处理层主要分为三个部分,数据挖掘、数据分析和数据聚合。数据挖掘是在海量数据中挖掘出对营销业务的有用信息;数据分析是对数据的正确性进行分析,保证数据的真实性;数据聚合是对同类数据进行整合、利用传输和保存[6]。
数据集分析层主要为大数据分析模型,通过对数据的分析,预测用户用电的需求和电站的状态,分析电力营销的规律。大数据模型经过不断的发展和创新,已经具有相当成熟的理论基础,进行相应的改进即可投入使用。
2 关键技术设计
2.1 基于实数取模运算的全同态数据加密方案
全同态加密方案由密钥生成算法、加密算法、解密算法和求值算法四个算法组成。本文的实数的运算法则是将非整数的小数部分进行转化成整数,然后按照整数的运算方法进行相应的运算,提出一种实数取模运算来进行转化[7]。
假设一个任意的正整数p和一个任意的实数n满足:
n=kp+r
(1)
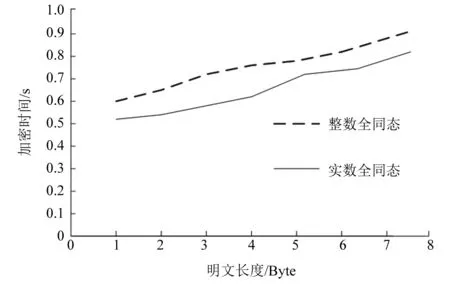
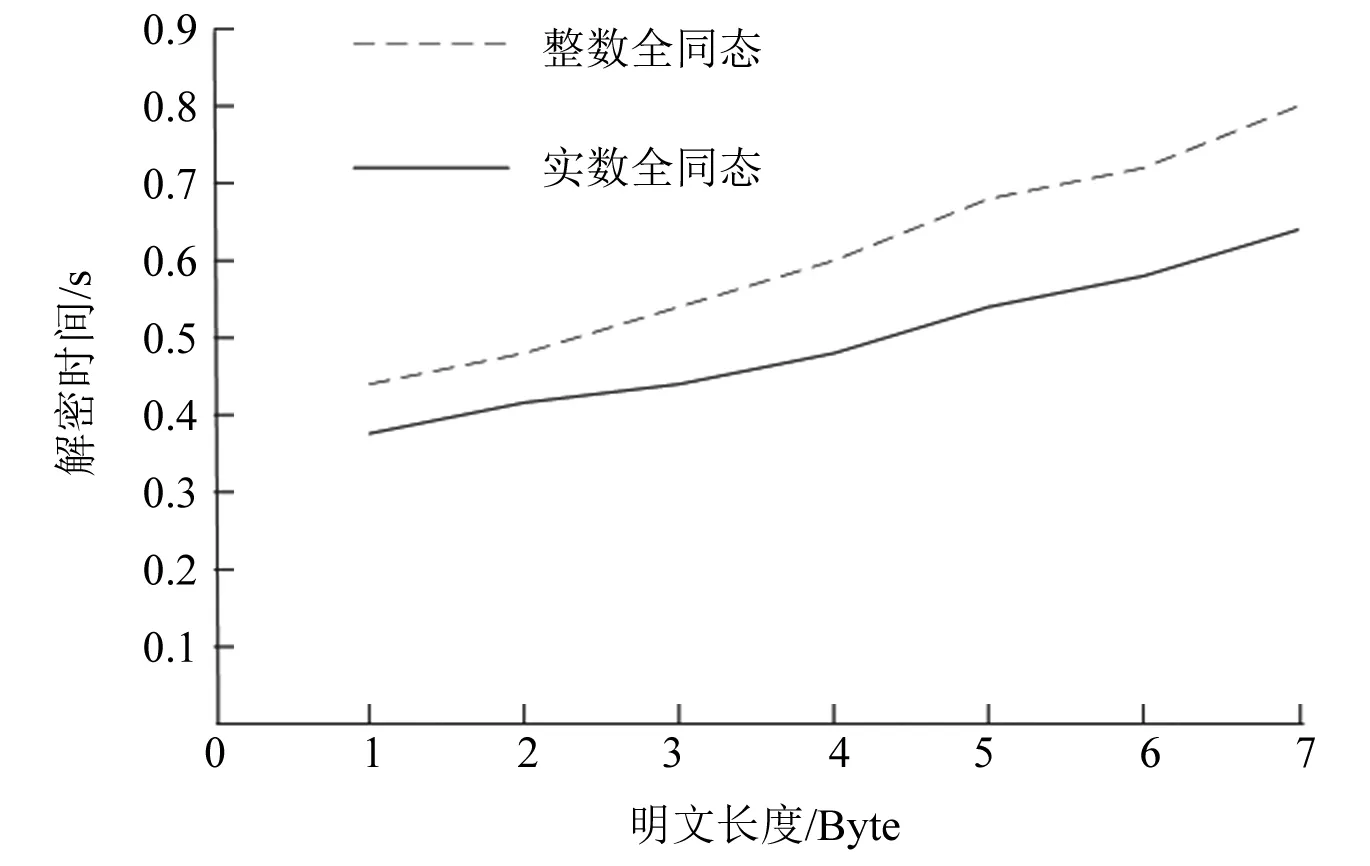
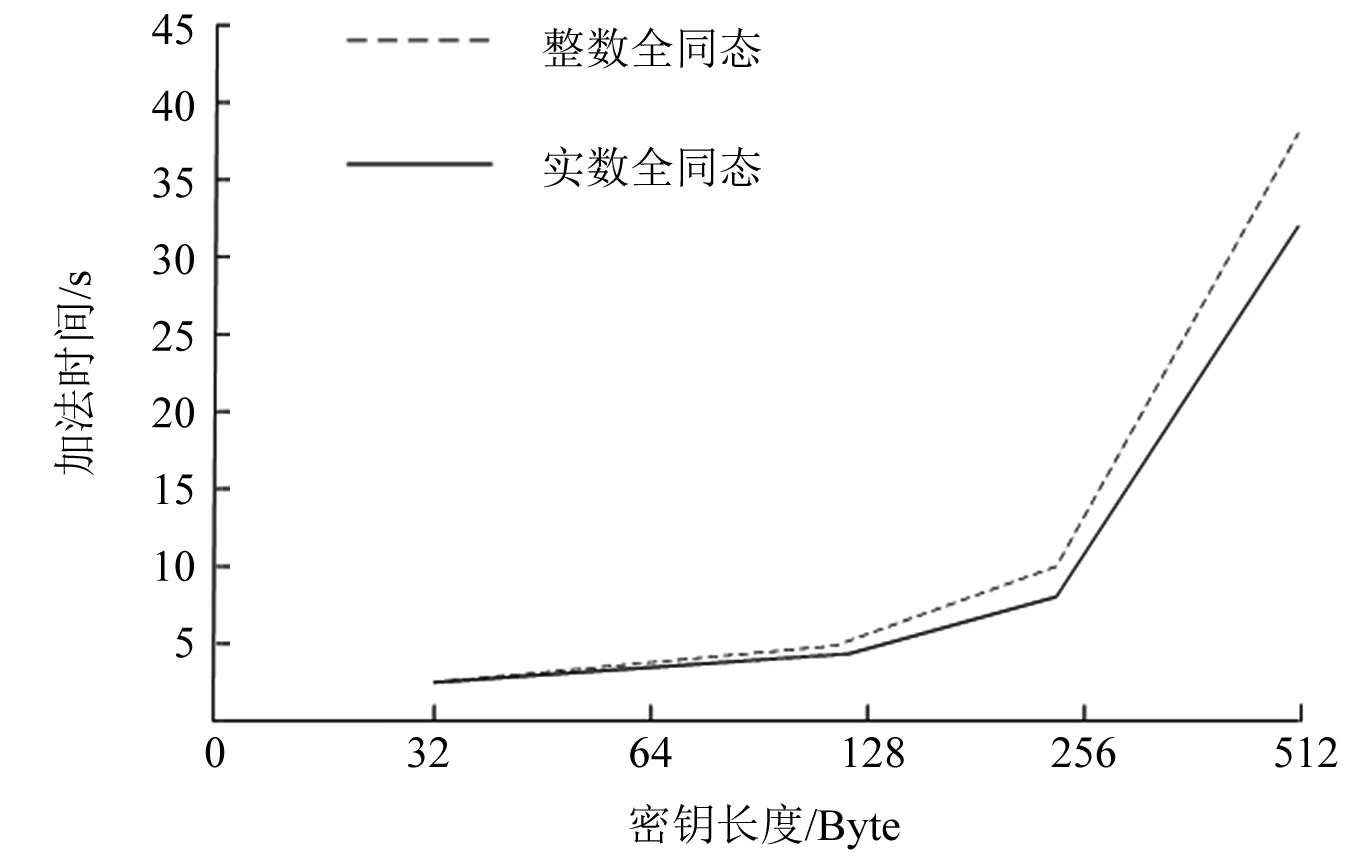
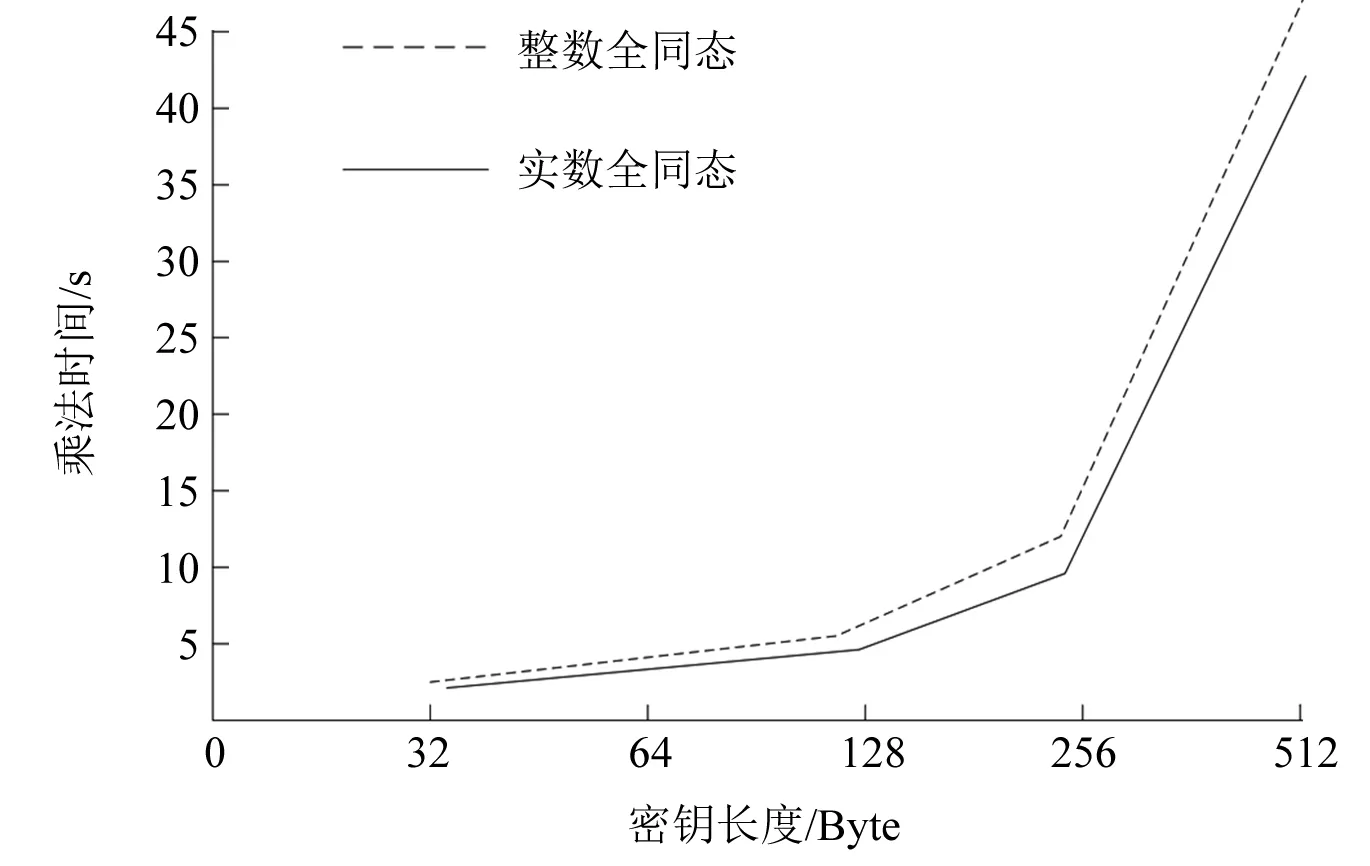
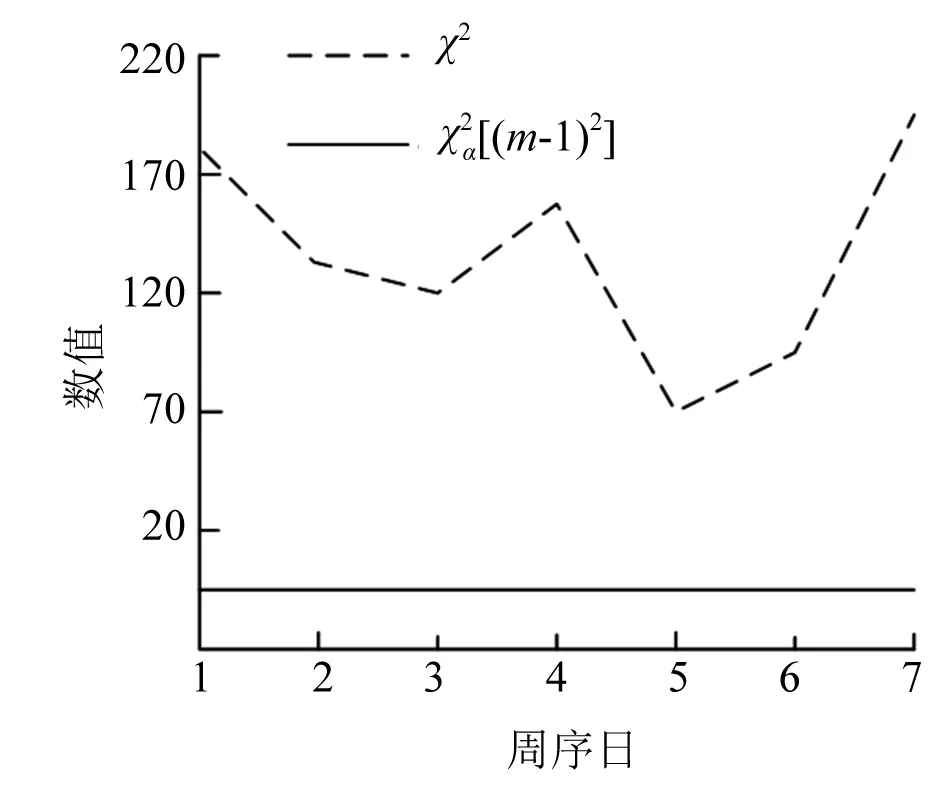
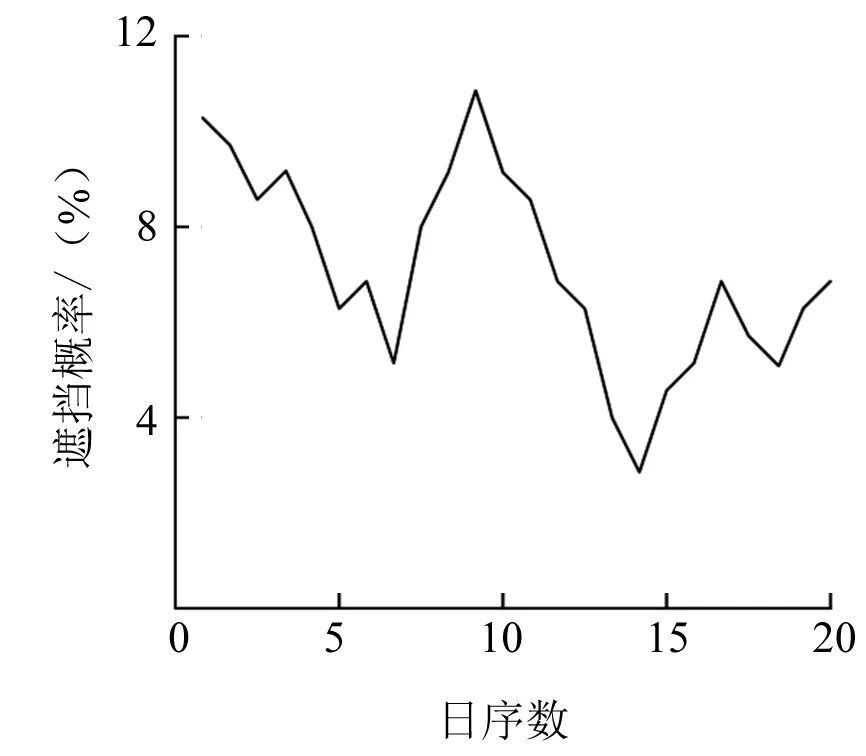
式中:k为整数,r为实数,并且0≤r 实数取模的运算公式为: (2) 通过式(2)的取模运算可以将全同态的数据加密方案扩展到实数范围,运用到工业控制系统中数据的加密中,以提高数据的安全性[8]。 数据加密主要是将数据通过密钥进行运算转化成密文,需要用到的时候再通过运算进行解密的一种保护数据安全的方式,将全同态数据加密的运算范围扩展到实数,不仅提高了全同态数据加密的适用性,还提高了数据加密的可靠性。 光伏电站的输出功率会受到光伏组件的受光面积、负载电压和太阳强度的影响。太阳能电池的I-U公式为: (3) 式中:I为太能能电池的输出电流;IL为光生电流;I0为电池反向饱和电流;q为电子的电荷;U为负载电压;n为二极管理想因子;k为玻尔兹曼常数;T为绝对温度。 本文提出一种基于温度系数的电流线性功率模型。根据式(3)可知,当电压U=0时,短路电流ISC=IL,即短路电流ISC与辐射度的强度成正比。假设工作环境的温度不变,光伏组件的短路电流ISC的计算公式为: (4) 式中:Gc为有效辐射度强度;ISC0、T0、G0为地面光伏组件标准测试(STC)条件下的短路电流、工作温度和辐照度;β为短路电流温度系数;Tc为光伏组件的实际工作温度。 由式(3)和式(4)可以推导出STC环境下的短路电流ISC0的计算公式为: (5) 式中:IMPP、UMPP为最大功率点电流和电压。 但是上述情况只有在理想情况下才能成立,在实际工作中光伏组件不可避免会受到阴影遮挡,导致计算出的ISC0计算结果会比理论值偏小。因此可以根据ISC0的计算结果来判断光伏组件是否被遮挡以及被遮挡的时间。 马尔科夫链是一种随机过程模型,即当前时刻的状态能够决定下一时刻的状态,不必考虑之前状态的影响[9]。假设现有一随机过程A={X1,X2,…,Xn}为马尔科夫链,离散状态集合I={a1,a2,…,an},a∈R,则其状态转移概率计算公式为: Pij=P{Xt+1=aj|Xt=ai} (6) 式中:Pij为从状态i转移到状态j的概率;Xt+1为t+1时刻的状态;Xt为t时刻的状态。 通常随机过程A会存在多个状态,因此P可以用矩阵的形式来表示。 (7) 矩阵P可称为一歩状态转移概率矩阵,则第k步的状态转移概率公式为: (8) 根据式(8),当k=2时,P(2)为1阶状态转移概率矩阵P中第i行各元素与第j行各元素对应相乘之和,其计算公式为: P(2)=P·P (9) 根据式(9)可以得出第n步的状态转移矩阵为: (10) 对于光伏组件的遮挡分析,初始数据为产生的电流,由于产生的电流数值范围较大,需要进行零-均值规范化处理。处理公式为: (11) 除此之外,还要获取异常的电流数据,即光伏组件发生遮挡时的短路电流。采用的是箱型图异常值分析法,箱型图会提供一个标准来识别异常值,异常值通常被定义为 光伏电站的遮挡概率计算模型的具体步骤为:采集光伏电站每日8∶00—18∶00的电站电流数据,将数据转化到STC条件下并进行零-均值规范化处理。然后采用箱型图分析法确定异常值构成马可科夫链,分别计算出正常数据的个数和遮挡时刻的个数,根据计算结果构建出非遮挡和遮挡两个状态的概率转移矩阵[9]。最后,通过“马氏性”检验后计算n步转移后的概率矩阵求出极限概率,即得到了光伏电站在运行时间内的遮挡概率。 在实验室内对上述数据加密算法和光伏电站的遮挡诊断算法进行仿真,以验证其可行性。采用的计算机配置为Windows 1064位操作系统,CUP为Inter Core i7-9700H,运行内存为16 G 3 200 MHz,硬盘大小为500 G。 上述改进中将全同态数据加密方案的运算范围从整数扩充到了实数,本文采用整数全同态数据加密方案(整数全同态)和数据加密方案(实数全同态)进行对比试验来比较两种方案的性能。首先对两种方案的加密时间和机密时间进行对比,在密钥长度为128 bit的情况下,比较两种方案对不同长度的数据加密时间和解密时间进行统计,加密时间对比示意图如图2所示。 图2 两种方案的加密时间对比 从图2可以看出,在相同密钥长度的情况下,随着明文长度的增加两种方案的加密时间会有所增长,但是实数全同态的数据加密时间会比整数全同态的加密需要的时间少。解密时间对比曲线如图3所示。 图3 两种方案的解密时间对比 在相同明文长度下比较两种方案在不同密钥长度下的加法和乘法运算时间,将测试结果进行整理。加法运算时间对比曲线如图4所示。 从图4可以看出在密钥长度<128 bit时,两种方案的加法时间几乎相等。但是密钥长度>128 bit字节之后,实数全同态的数据加密方案的加法算法增长速度会低于实数全同态。两种方案的乘法算法时间如图5所示。 图4 两种方案的加法算法时间对比 从图5可以看出,在密钥长度<128 bit时,两种方案的乘法时间几乎相等。但是密钥长度>128 bit字节之后,实数全同态的数据加密方案的乘法算法时间增长速度会低于实数全同态。 图5 两种方案的乘法算法时间对比 综上所述,将全同态数据加密的运算范围扩展到实数能够提高运算效率。 选取南通市内某光伏电站作为数据的来源,对电站内的电流、电压、辐照度和环境温度进行采集。采集频率为每两分钟一次,根据电站使用的多晶硅光伏组件品牌查得其温度系数β为0.06%,I0为5.82 nA,n为1.15。采集的时间为2019年11月21—30日,将这10 d的数据作为初始数据。 首先对数据进行预处理,采用上述的零-均值规范法。数据处理完成后,采用箱型图分析法分析得到电流的异常数据,即发生遮挡时的电流数据。分析一共得到45个异常数据,所处时间段大多为15∶00—18∶00。根据遮挡和非遮挡状态下的电流数据可以建立一歩转移概率矩阵: (12) 式中:PAA为当前时刻状态和下一时刻状态都为遮挡状态的概率;PAB为当前时刻状态为遮挡状态,下一时刻状态变成非遮挡状态的概率,以此类推。 将电流异常数据代入到式(10)中,可以得到d1的一歩状态转移概率矩阵: (13) 然后对数据进行 “马氏性”检验,采用χ2作为检验的标准。假设一数据序列的状态数为n,状态空间I={1,2,3,…,n},则边际概率的计算公式为: (14) 式中:P·j为边际概率;fij为转移频数概率矩阵。 根据式(14)的计算结果,可以得到χ2的计算公式为: (15) 图6 χ2与值对比图 本文将采集的每日数据构成马尔科夫链,因此马尔科夫链长度都是有限的,满足以下性质: (16) 式中:若Pj≥0,则{Pj,j=1,2,…,N}构成了一个概率分布,若{Pj,j=1,2,…,N}同时又满足Pj=Sipipij(Pj为状态为j的概率值;pi为状态为i的概率值;Si为i从0到N的和),则可以称为平稳分布。平稳分布的有限状态马尔科夫链具有以下性质:转移概率与初始状态无关,且一定为平稳分布。根据以上性质,设置转移步数为100,则d1序列的极限概率为: (17) 根据式(17)的计算结果可知,d1序列的遮挡概率为9%,即在1 d的运行过程中,有9%的时间被遮挡。 根据以上的计算过程,计算20 d的遮挡概率,可以得到遮挡概率统计如图7所示。 图7 遮挡概率统计图 根据图7可知,20 d的遮挡概率在3%~10%之间,与实际的运行情况基本相同。基于以上内容,可以得出本文的光伏电站遮挡计算模型,能够根据电流数据准确地计算出被遮挡的概率。 本文以数据隐私性和光伏电站的监测为出发点,对电力营销业务的管控进行了改进,使其能够满足互联网时代的要求。通过仿真,验证了加密算法和光伏电站遮挡概率计算的可行性,在电力营销管控方面具有良好的应用前景。但是由于试验数据不足,结果可能会存在一定的误差,在后续的研究中需要不断优化。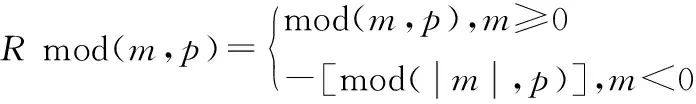
2.2 基于马尔代夫链的光伏电站遮挡概率预测算法
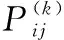
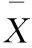
3 试验仿真与分析
3.1 数据加密方案性能验证
3.2 光伏电站遮挡预测模型仿真
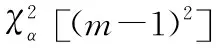
4 结束语

