基于线圈辅助励磁模型的无刷直流电动机调速控制系统设计

陈弘

(福建省送变电工程有限公司 ，福建 福州 350001)

0 引 言

无刷直流电动机多为自动控制模式，因此对无刷直流电动机输出稳定性的要求较高。研究无刷直流电动机的调速控制方法，在无刷直流电动机的优化设计中具有重要意义，相关的无刷直流电动机转速调节控制方法研究受到人们的极大重视[1]。

当前，对无刷直流电动机的调速控制方法主要为模糊控制方法、PID控制方法和反馈控制方法等[2-3]。文献[4]提出基于非同步耦合调制的无刷直流电动机的调速控制方法，采用自适应转速参数识别方法进行电机的输出稳定性控制。但该方法的计算量较大，抗扰动性不好。文献[5]提出基于模糊PID的电机转速控制方法，通过增加虚拟阻尼电阻进行无刷直流电动机的虚拟同步控制。该方法进行无刷直流电动机调速控制的模糊度较大，参数辨识能力不好。

针对上述方法存在的问题，提出基于线圈辅助励磁模型(以下简称BLDCM模型)的无刷直流电动机调速控制系统设计方法。首先构建控制约束参量模型；然后采用MMC子模块跟踪调节方法构建无刷直流电动机调速控制的动态约束规划模型，采用柔性直流输电换流BLDCM模型进行无刷直流电动机的输出转速稳态控制；最后进行仿真测试分析，得出有效性结论。

1 控制对象及约束参数分析

1.1 无刷直流电动机调速控制对象分析

构建无刷直流电动机调速系统的等效电路模型和被控对象模型，无刷直流电动机的等效传输原理图如图1所示。图1的等效电路模型分为初级电路和次级电路，采用电磁耦合器进行无刷直流电动机的等效传输的互感耦合控制[6]，建立等效T型电路，如图2所示。

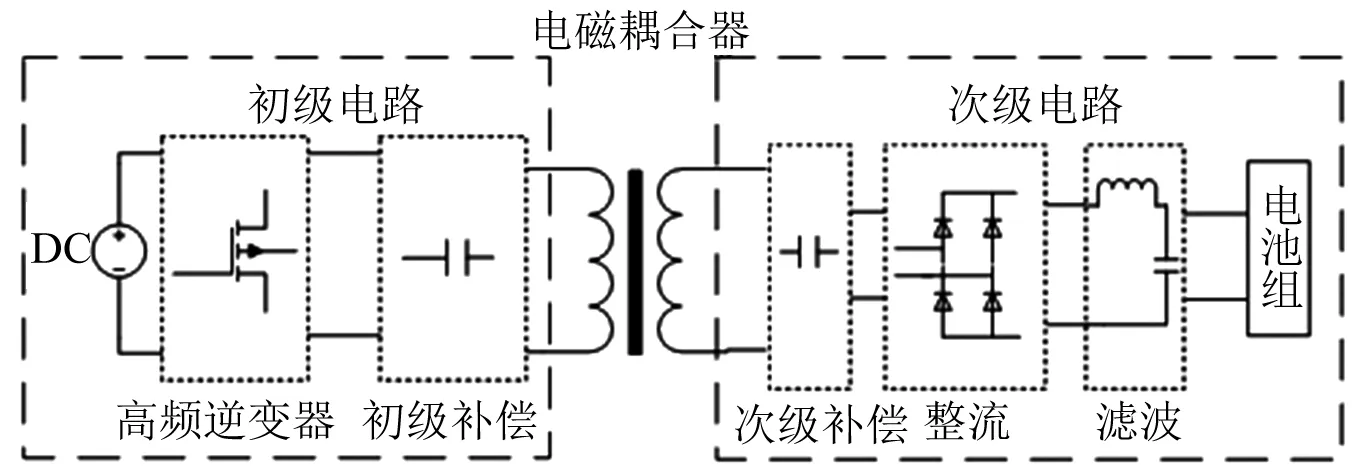
图1 无刷直流电动机的等效传输原理图

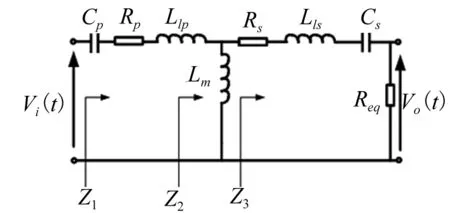
图2 T型等效电路

根据图2可知，无刷直流电动机的抗饱和控制过程是一个包含多变量的多目标优化过程。进行无刷直流电动机的调速控制时[7]，输出平均功率变化率为f，计算无刷直流电动机的直流控制变量。通过多时空尺度协调方法进行无刷直流电动机的输出等效控制，得到无刷直流电动机的输出相位和角频率的相关矩阵，具体表示为：

(1)

式中：G11(s)、G22(s)为无刷直流电动机输出相位；A12(s)、A21(s)为角频率；s为时间；e为单位时间电子量。在时间尺度上逐层细化电机变频过程，得到无刷直流电动机的失稳补偿反馈调节函数，计算电功率预测值[8]，得到无刷直流电动机的调速自动控制方程，如式(2)所示。

(2)

式中:v(k)为无刷直流电动机直流电压输入信号；x1(k)为确定的扰动步长下的无刷直流电动机输出阻抗；x2为电机组的减载控制参数；h为双闭环控制的步长；h0为双闭环初始步长。采用振荡失稳抑制方法进行无刷直流电动机转速控制过程中的稳定性调节和误差补偿，建立失稳补偿和反馈调节函数，在调频的空间范围内，采用负荷的波动性调节方法进行无刷直流电动机的直流多功率稳态调节，提高无刷直流电动机的自适应控制能力[9]。

1.2 控制约束参量模型

构建无刷直流电动机调速控制的约束参量模型，以直流输电的功率损耗和电机转矩为约束参量[10]，得到无刷直流电动机调速控制的目标函数，如式(3)所示。

f0(X)=wpP(X)+ε

(3)

式中：wp为功率损耗；P(X)为电机转矩；ε为一个小的常数，表示AGC电源协调配合的模型控制参数。

引入启动时间顺序、调频持续时间进行输出耦合控制，得到三次调频控制的迭代方程为：

(4)

xid=xid+Vid

(5)

式中：w为无刷直流电动机的磁损耗惯性权重；c1和c2为电功率预测约束的加速度常数；rand()和Rand()为两个在[0,1]范围里变化的随机值；pid、xid分别为启动时间顺序及调频持续时间。采用MMC子模块跟踪调节方法构建无刷直流电动机调速控制的动态约束规划模型，进行调速控制系统的优化设计。

2 无刷直流电动机调速控制算法优化

2.1 BLDCM模型

BLDCM是一种非线性控制系统，构建BLDCM模型，能够应用于无刷直流电动机调速控制系统中，得到较好的控制效果。使用AGC电源进行无刷直流电动机调速过程中的模糊度控制，构建无刷直流电动机调速增益调节模型。无刷直流电动机混合双馈控制模型表示为：

(6)

式中：p1、p2为无刷直流电动机的直流输电最大功率点因素；j为功率平衡约束参数；p3为升压比例；β为最优控制增量作用下的可调参数。

考虑系统网络拓扑结构，计算无刷直流电动机的调速控制误差项，得到无刷直流电动机自适应调节函数。

(7)

式中:α1、α2、δ1、δ2、b0为三次调频层控制时域特征系数；kp、kd为比例系数和微分系数。通过自适应调节函数进行电动机的电容电压监测，得到实时性控制律为：

(8)

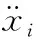
(9)

根据上述BLDCM模型设计，结合模糊参数约束方法进行无刷直流电动机调速自适应控制。

2.2 电动机调速控制输出

采用MMC子模块跟踪调节方法构建无刷直流电动机调速控制的动态约束规划模型，采用柔性直流输电换流BLDCM模型进行无刷直流电动机的输出转速稳态控制，得到输出的电压增益为：

(10)

能量损失相对大小的损耗比为：

(11)

式中：Req为能量损失量。在子模块电容电压波动下，单边复合次级直线感应电机的整流扰动输出为：

(12)

在二维电磁模型中进行扰动控制，根据并联过程的电压变化进行无刷直流电动机调速控制。

3 试验分析

为了验证本文方法实现无刷直流电动机调速控制的应用性能，进行了仿真测试。选用电动机型号为57BL-1080H1-LS-B，额定输出功率为10 MW，额定电压220 V，额定转速3 000 r/min。电动机实例如图3所示。

图3 电动机实例

设定无刷直流电动机的输出磁密在1.45到2.58之间取值,单元电机等效磁路的转矩输出为36 N·m，三相额定电流为210 A，其他参数设计见表1。

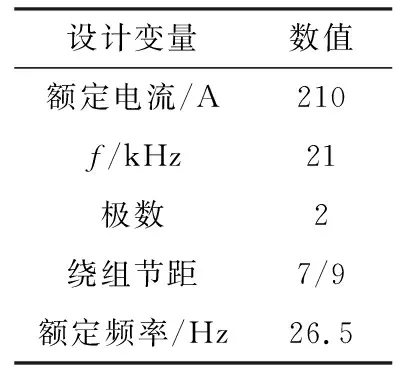
表1 参数设计

采用MATLAB软件为仿真试验环境，在MATLAB平台搭建所设计的基于BLDCM模型的无刷直流电动机调速控制系统。采用文献[4]方法、文献[5]方法作为试验对比方法。

根据上述仿真环境和参量设置，进行无刷直流电动机调速控制，测试无刷直流电动机的输入最大电流与时间的关系，结果如图4所示。

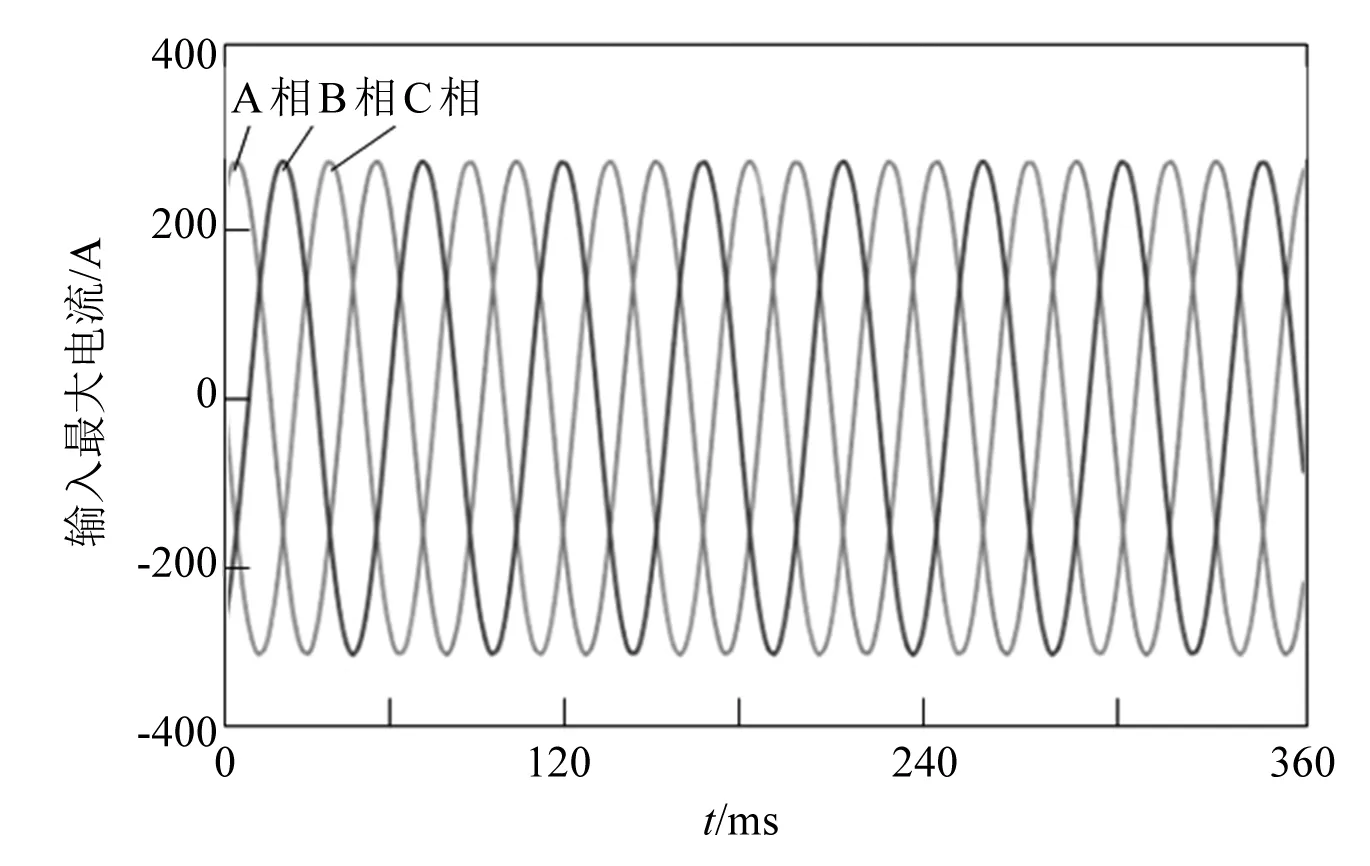
图4 输入最大电流与时间的关系

分析图4可知，采用本文方法进行电动机调速控制，输入电流的稳定性较好。以此为基础，分别测试本文方法及两种对比方法的输出功率，得到结果如图5所示。

分析图5得知，采用文献[4]、文献[5]方法进行无刷直流电动机调速控制时，其输出功率波动较大，而采用所提方法进行无刷直流电动机调速控制时，其输出功率波动小，平稳性较好。

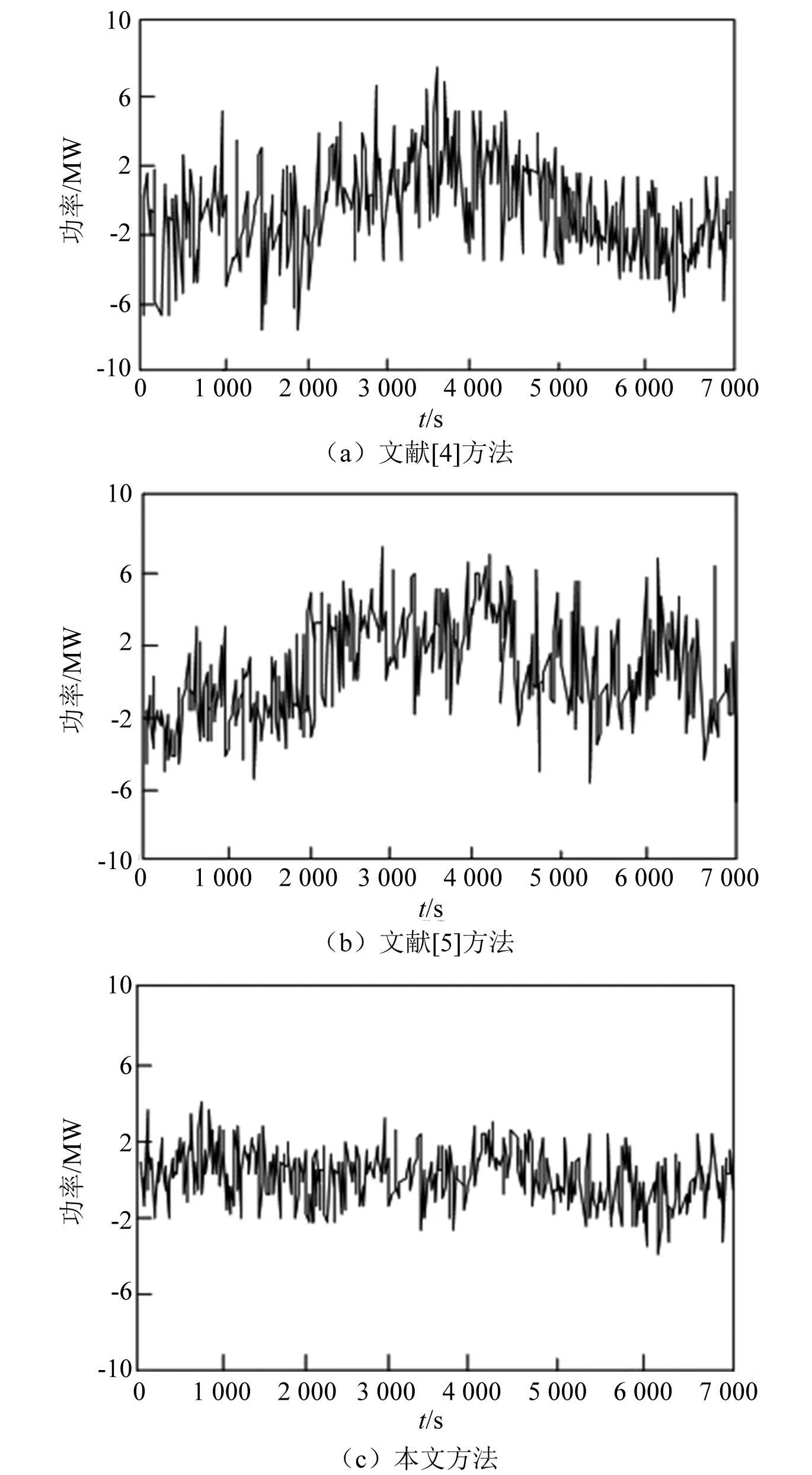
图5 输出功率测试对比结果

采用3种方法进行调速控制，迭代次数500次，测试控制的精度，得到结果如图6所示。

分析图6可知，采用文献[4]方法进行无刷直流电动机调速控制，在迭代500次后的控制精度为0.918，采用文献[4]方法进行无刷直流电动机调速控制的控制精度为0.911，而采用所提方法进行无刷直流电动机调速控制的控制精度为0.982。试验结果表明，采用所提方法进行无刷直流电动机调速控制的精度较高。

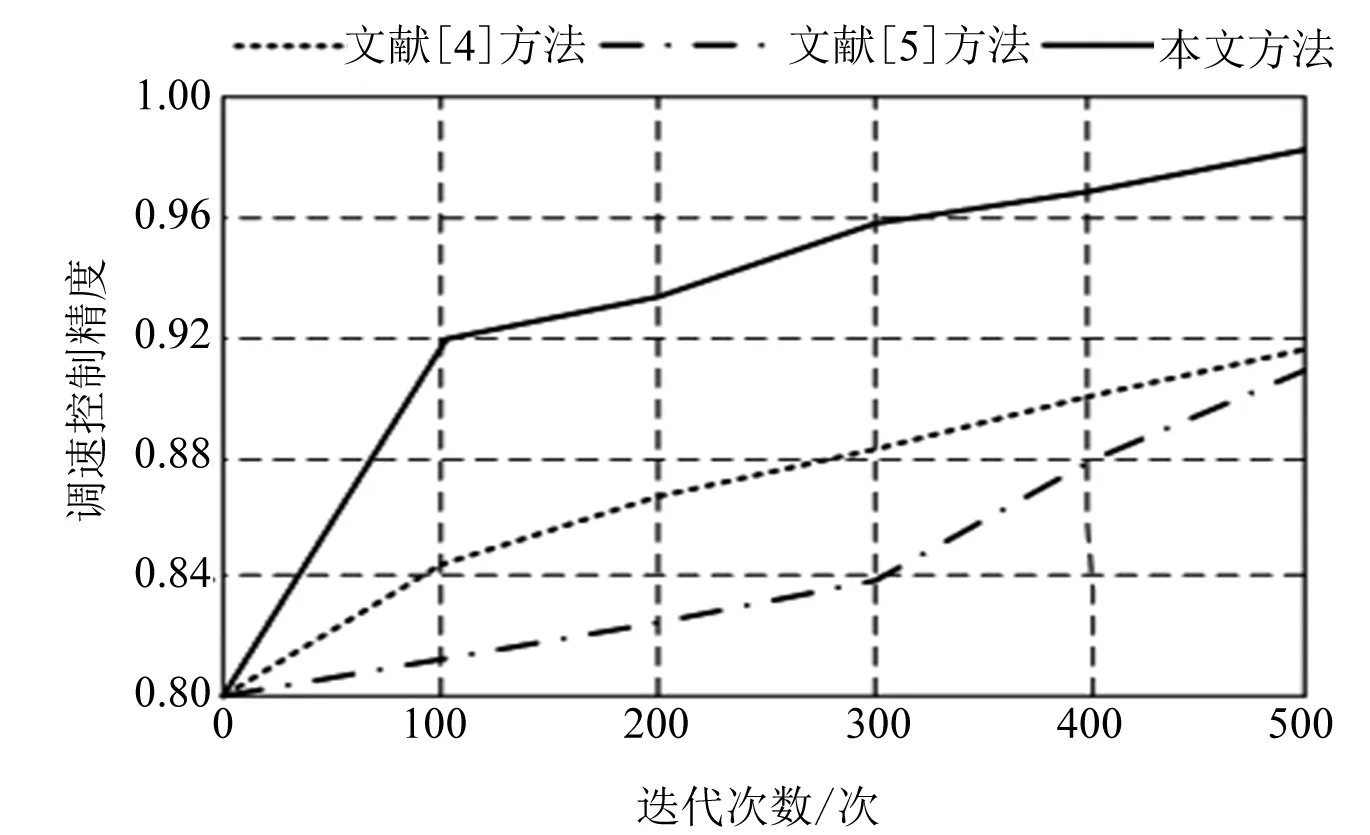
图6 控制精度测试

4 结束语

本文提出基于BLDCM模型的无刷直流电动机调速控制系统设计方法。采用电磁耦合器进行无刷直流电动机的等效传输的互感耦合控制，构建无刷直流电动机调速增益调节模型。采用柔性直流输电换流BLDCM模型进行无刷直流电动机的输出转速稳态控制。分析得知，采用本文方法进行无刷直流电动机调速控制的输出稳定性较好，电动机的输出功率增益得到提升。