基于改进混沌粒子群算法的电压暂降状态估计

褚晨杰， 吕干云， 贾德香， 吴晨媛， 李军

(1.南京工程学院 电力工程学院，江苏 南京 211167；2.国网能源研究院有限公司，北京 102209；3.国网常州供电公司，江苏 常州 213000)

0 引 言

电压暂降作为电能质量的主要指标之一，它给电力系统和用户的敏感供用电设备造成了一系列严重的问题[1]，包括照明设备、交流接触器、调速电机及多种工业设备的运行异常[2]。

近年来，电压暂降状态估计(voltage sag state estimation, VSSE)的概念被一些学者提出。文献[3]较早提出一种针对辐射型电网的电压暂降状态估计方法，采用最小二乘法搜索故障点所在路径，从而估计非监测节点电压暂降幅值，但该方法在环网中并不适用。文献[4]提出了一种基于实测的统计分析法，根据中高压变电站的暂降特性估计系统的暂降频次，但存在监测设备成本较高、统计结果易受环境和人为因素影响等问题。文献[5-6]等则采用量子粒子群和仿电磁学算法实现了电压暂降频次状态估计，并引入历史故障数据有效提升了估计精度。

本文通过电压暂降频次来刻画和估计电网中的暂降信息。通过可观测区域(monitor reach area,MRA)法配置监测仪安装位置，使用解析式法和故障点法确定故障区间和观测矩阵。然后将历史故障数据和现有监控数据结合，构建VSSE模型。最后将Tent映射具有遍历均匀性、迭代速度快的优点和莱维飞行方式相结合引入粒子群算法，提出一种改进混沌粒子群(chaotic particle swarm optimization, CPSO)算法，增强了全局寻优性能。通过在IEEE 30节点系统中测试，验证了本文算法的准确性和有效性。

1 VSSE的基本原理及模型

1.1 电压暂降状态估计的原理

VSSE的基本原理是通过监测母线上获得的暂降频次来估计未监测母线的暂降频次，其数学表达式为：

H=MX+ε

(1)

式中：H为量测量,H中各元素表示在对应电压阈值下监测母线上记录的电压暂降频次;X为状态变量;M为系统的观测矩阵;ε为量测误差。

1.2 量测量矩阵H的建立

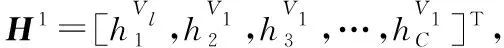
1.3 状态变量矩阵的建立

X中各元素表示对应的故障区间内发生故障的次数。本文基于故障点法进行故障区间划分，图1为母线m1沿线路发生故障时的电压暂降曲线，横轴表示故障位置百分比；纵轴表示残余电压率。图1中故障点随机选取在p1、p2处，线路的故障区间可用a、b两段表示。由于实际系统中存在过渡电阻和负荷变化等因素，母线电压暂降实际值与故障电压估计值偏差较大，从而影响了VSSE精度。因此故障区间划分的合理性直接影响状态估计结果的精度。本文将每条线路平均分为十段，由于临近的故障点造成的故障电压非常接近，因此故障点的选取不会对结果产生太大影响。

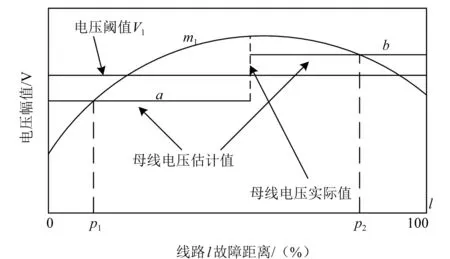
图1 母线的电压暂降曲线

1.4 观测矩阵M的建立

在阈值电压V1下观测矩阵M1的构建过程如下：

(2)

式中：Vij为故障区间j处发生故障时节点i处电压值；L为线路总数；C为监测仪总数。图1中，若l为第一条线路，当沿线路l发生短路故障时，监测母线m1在故障区间a的残余电压小于阈值电压V1，则M1(1,1)=1；故障区间b的残余电压高于阈值电压V1，则M1(1,2)=0；遍历全网所有线路则形成观测矩阵M1。

1.5 VSSE目标函数及约束条件

为了使VSSE结果在实际工程应用中更具有可靠性，本文的目标函数如下：

(3)

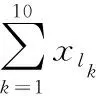
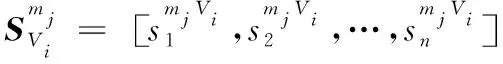
状态变量还应满足以下约束条件:

(4)

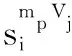
2 改进混沌粒子群算法

标准PSO算法在求解VSSE这类高维度和多局部极值问题时，在后期全局搜索能力不足，易出现早熟问题。因此本文采用一种改进混沌粒子群算法，利用混沌搜索的遍历性以及莱维飞行保持种群多样性来改进PSO算法，克服了PSO算法陷入局部最优的缺陷，寻优能力更强。利用莱维飞行的随机步长特点，加强脱离局部最优的能力，改进后的速度和位置更新如式(5)、式(6)所示。

vid(k+1)=w×vid(k)+[c1⊕L(λ)][Pid(k)-xid(k)]+
[c2⊕L(λ)][Pgd(k)-xid(k)]

(5)

xid(k+1)=xid(k)+vid(k+1)

(6)

式中：w为惯性权重；c1、c2为学习因子；Pid(k)、Pgd(k)分别为个体最优解和全局最优解；k为当前迭代次数；L(λ)为Lévy随机搜索路径，服从下式Lévy分布：

L(s,λ)～s-λ,(1<λ≤3)

(7)

式中：s为由Lévy飞行得到的随机步长。第二阶段：通过Tent映射将粒子映射到混沌空间中，使粒子可以飞行至全部的解集空间。Tent映射的数学表达式为：

(8)

对位置变量xid基于Tent映射进行混沌搜索，对比搜索前后适应度值，更新xid。

3 改进混沌粒子群算法求解VSSE

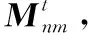
图2 改进CPSO求解VSSE的流程

4 算例分析

将本文方法应用于IEEE 30节点系统，系统结构如图3所示。该系统有30个节点、5座发电机和37条线路。本文故障类型设定为三相短路故障，不对称故障数据参见文献[7]。

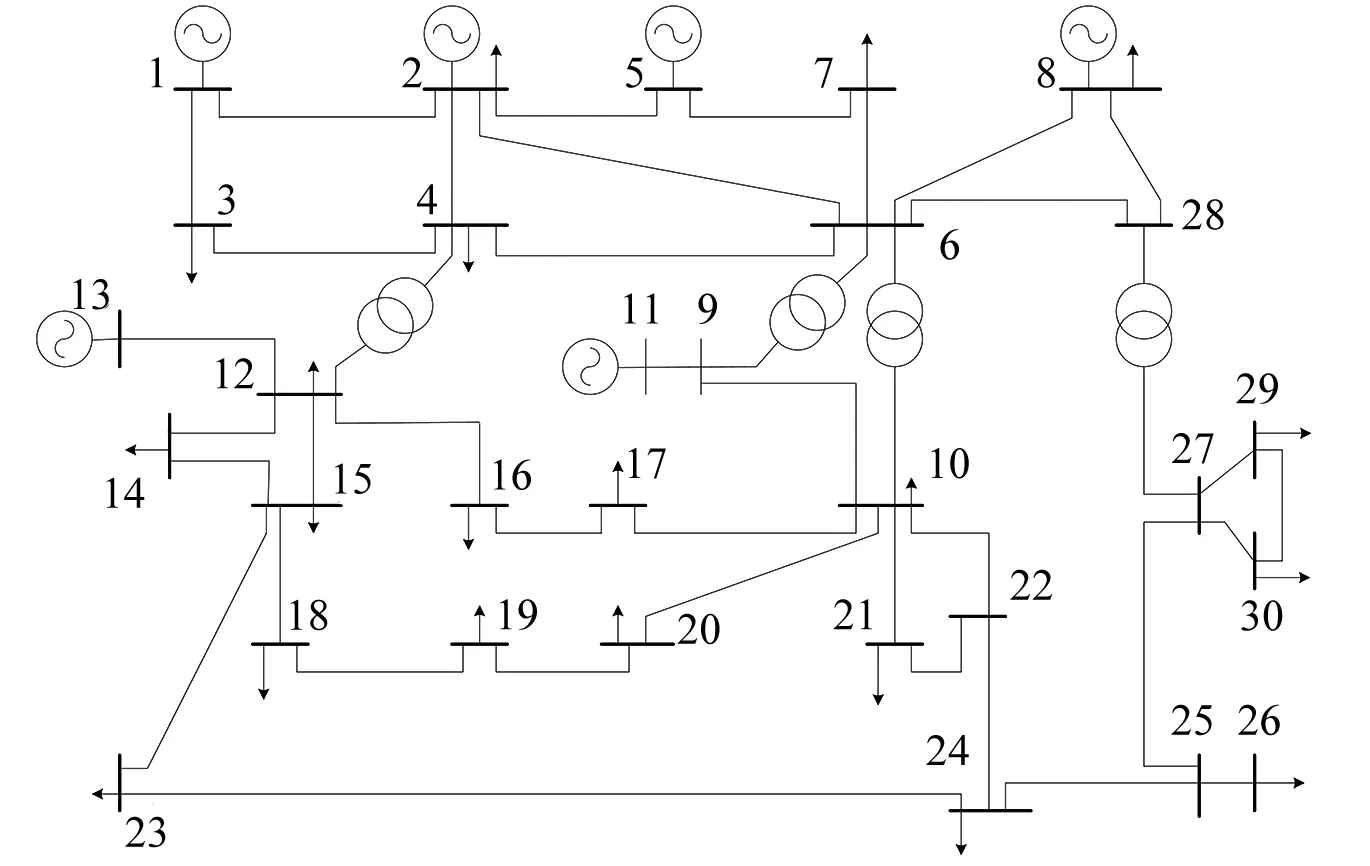
图3 IEEE 30节点系统

本文以电压阈值0.8 pu配置监测点，历史故障数据使用参考文献[8]中方法获得。在本文仿真分析中利用蒙特克罗随机模拟法在线路历史故障点附近随机模拟每条线路的故障位置。将本文改进CPSO算法与GA、PSO算法分别求解VSSE的结果对比，不同算法的平均适应度比较如图4所示。图5描绘了电压阈值为0.8 pu时母线电压暂降频次的实际值和估计值。

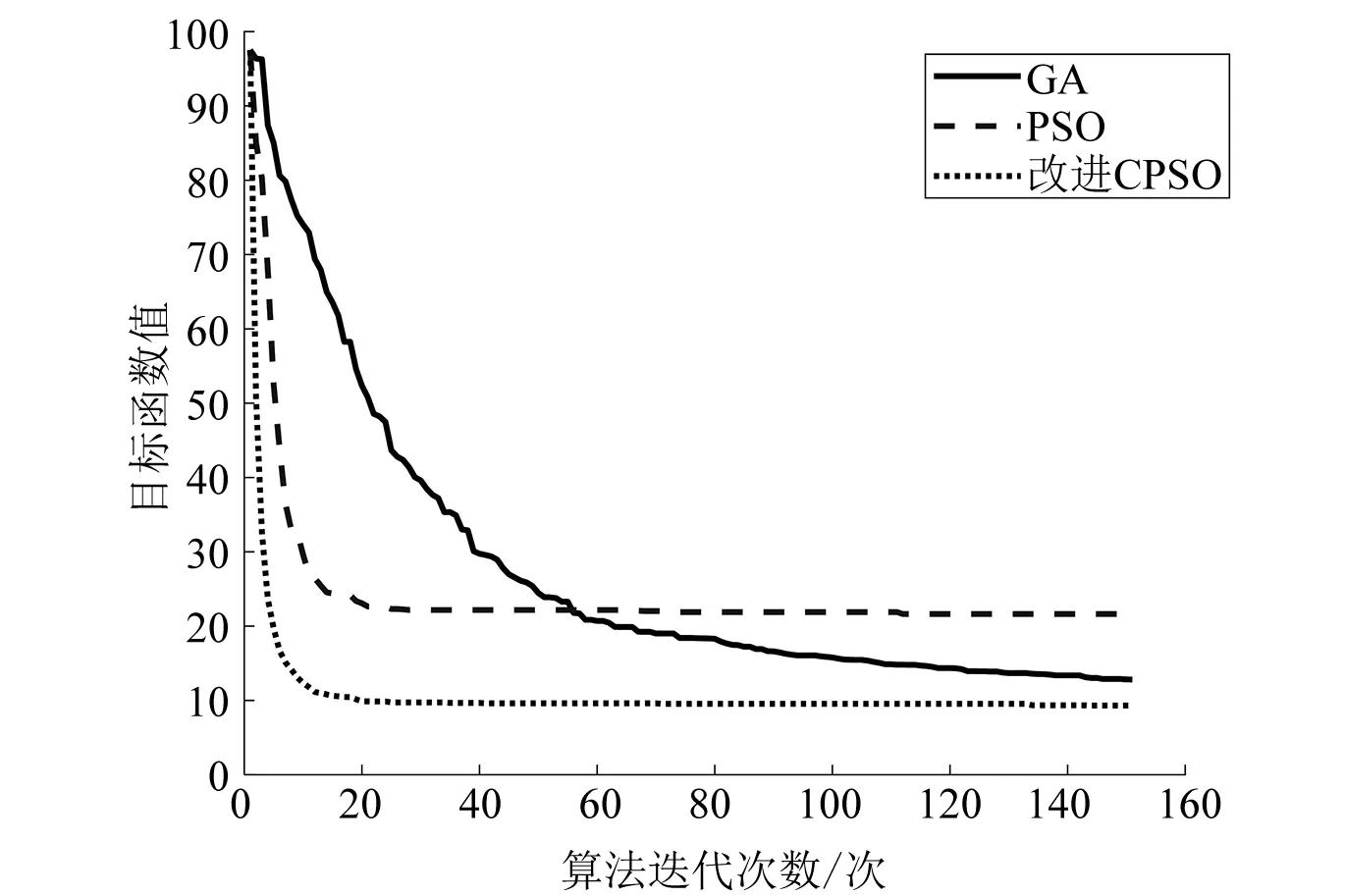
图4 不同算法的平均适应度比较

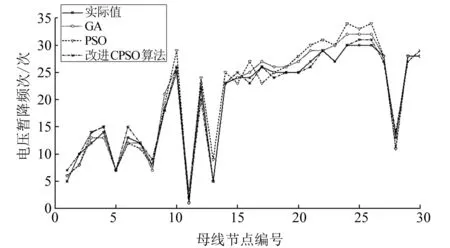
图5 电压阈值为0.8 pu时估计结果

从图4可以看出,改进CPSO算法的迭代收敛速度最快，在迭代进行20次时就已经有较好的寻优结果。为了评估文中估计值的准确性，定义误差为:

(9)

式中：REj为第j个节点的估计误差；NSest,j、NSreal,j分别为第j个节点的暂降频次估计值和实际值；NSequal为整个电网在某一阈值下的节点电压暂降频次均值。按图2求解流程，将改进CPSO算法和GA、PSO算法的仿真统计结果及误差对比列于表1、表2。

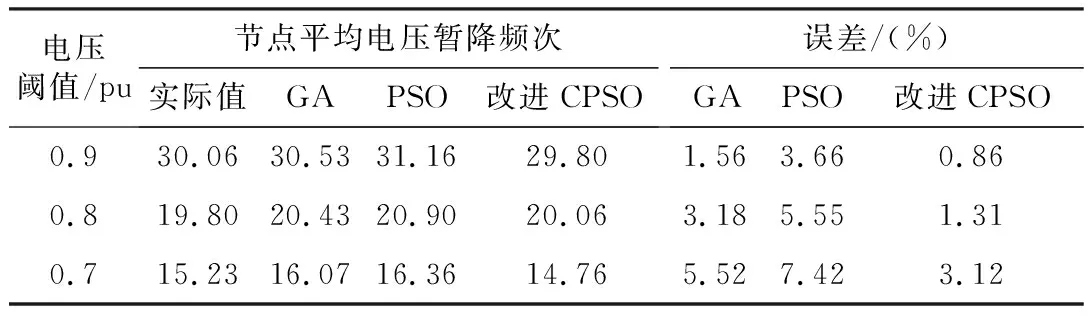
表1 节点平均电压暂降频次

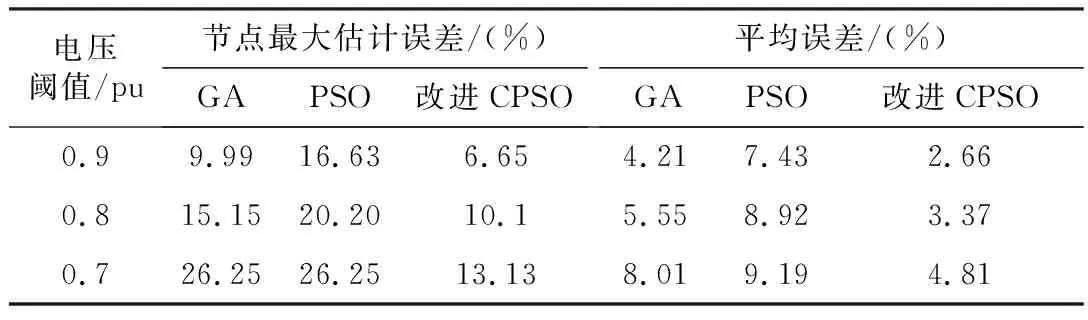
表2 IEEE 30节点仿真结果误差

通过表1和表2的误差对比可知，改进CPSO算法估计出的节点平均电压暂降频次高度接近于实际值，其精度明显优于GA、PSO算法，拥有较高的准确性。另外随着电压阈值的降低，平均误差逐渐增高，这是因为本文以电压阈值0.8 pu配置监测点，幅度低于0.8 pu的凹陷可能被遗漏从而导致电压暂降频次估计不准确。

5 结束语

本文提出一种基于Tent映射的改进CPSO算法，将莱维飞行和混沌搜索引入增强算法跳出局部最优的性能。利用该方法在IEEE 30节点系统中仿真测试，与标准GA、PSO算法的对比结果表明，改进CPSO算法的全局寻优能力强、寻优效率高和收敛性更好。VSSE虽然近年来取得了一定的进展，但仍面临复杂电网模型和参数的不确定性、时变性及量测不足的实际状况，解决这些问题是未来相当长时间内电能质量领域所面临的重要课题。