考虑静态电压稳定性的含风电场电力系统两阶段无功优化配置

朱维骏，杜振东，翁华，郁丹，刘晓芳

(浙江华云电力工程设计咨询有限公司，浙江 杭州 310006)

0 引 言

一般情况下，电压稳定问题与系统中无功不足的情况密切相关，属于静态稳定范畴。随着风电并网容量的增加，大规模风电场群并网后由于无功的波动而造成的含风电场电力系统电压稳定问题已成为当前风电并网亟需解决的问题，而实时跟踪系统无功的波动并进行补偿是解决这一问题的重要手段。

无功优化配置模型的决策变量通常是无功补偿装置的选址和容量，目标函数一般包括风险性指标项[1]70[2]3260[3]1153和经济性指标项[3]1153[4]31[5][6]1894。其中风险指标可分为两大类：一类通过连续潮流计算等方法，获取负荷裕度[7]等稳定性指标；一类是基于一般潮流计算得到的系统电压等电气量，构建的节点电压偏差和L指标[8-9]等评价指标。经济性指标主要包括无功补偿装置的网损、安装和维护费用等。同时，为了减小优化问题的规模，一般会通过灵敏度分析[1]70[10]和聚类[11]等方法筛选出候选补偿节点。

求解方法方面，由于交流潮流方程的非线性和非凸性，一般采用遗传算法和粒子群算法等启发式算法求解[1]71[2]3261[6]1894[12]，亦有文献通过线性化的方式将原非线性问题转化为凸优化问题[3]1154[4]44-46从而可以通过求解器直接求解或者结合启发式算法和数学规划方法[13]23-25。单纯采用遗传算法等启发式算法易导致“早熟”，陷入局部最优，解的质量难以得到保证。文献[13]28结合遗传算法和数学规划算法，但是对于交流潮流方程的处理不够细致。

基于现有研究的不足，本文提出一种考虑静态电压稳定性的两阶段无功优化配置框架：第一阶段利用L指标灵敏度的概念，确定无功补偿装置候选安装节点；第二阶段基于第一阶段的候选节点，进一步给出各个候选节点的无功补偿装置安装容量以及各个时段的动作情况。通过对交流潮流方程的线性化处理，将原问题转化为混合整数线性规划问题，同时优化过程综合考虑了不同的风电场景，给出的无功配置方案更能适应恶劣运行条件。

1 风电不确定性场景获取

风电不确定性场景采用如下方法获取：首先利用t-location scale分布[14]对历史风电出力预测误差进行拟合，再对拟合得到的概率密度函数进行拉丁超立方采样[15]，最后通过K-medoids聚类[16]获取典型场景及其概率。

2 基于L-Q灵敏度的候选节点选取

2.1 L指标

Kessel首次提出了L指标[17]，该指标可用于系统的静态电压稳定性的监测和评估。应用该指标进行电压稳定性分析时，首先需要把所有节点划分为两组：一组是负荷节点集合L，包括所有的PQ节点；另一组为发电机节点的集合G，包括所有的PV节点和平衡节点。

对节点进行分类后，系统的状态方程可表示为：

(1)

进一步变换可得：

(2)

式中：VL和VG分别为负荷节点和发电机节点的电压向量；IL和IG分别为负荷节点和发电机节点的注入电流向量；YLL、YLG、YGL、YGG分别为相应的导纳矩阵子矩阵。

定义负荷参与因子：

(3)

则负荷节点j的L指标可由式(4)计算：

(4)

每个负荷节点都可求得一个L指标值，一般取其中最大值作为整个系统的L指标值，用以评估系统的静态电压稳定性，即：

(5)

式中：αL=[1,2,…,nL]。L指标取值和静态电压稳定性之间的对应关系为：01，系统电压不稳定。

2.2 L-Q灵敏度

为了进一步减小优化问题的规模，提高求解效率，有必要事先确定候选配置节点，参考文献[1]70的思路，采用L-Q灵敏度指标(L-QSensitivity Index，LQSI)衡量在不同节点配置等容量无功补偿装置对于系统整体静态电压稳定性提升的效果。计算方法如式(6)所示。

(6)

式中：LQSIj为负荷节点j的L-Q灵敏度指标值；L为未配置无功补偿时的系统L指标；L(ΔQj)为在负荷节点j配置容量为ΔQ的无功补偿装置后的系统L指标；ΔQj为在负荷节点j配置的无功补偿容量，本文取为50 Mvar。

某节点的LQSI越大，说明在该节点配置同等容量无功补偿装置对系统静态电压稳定性的提升越明显，因此优先选择在LQSI较大的节点配置无功补偿装置。同时由于运行参数一定的情况下，补偿前的系统L指标为定值，因此LQSI越大等效为补偿后的系统L指标越小。

3 考虑多场景的无功优化配置模型

3.1 目标函数

目标函数可由式(7)表示，包括无功补偿装置的安装C1、维护费用C2、实际补偿费用C3、电容器调节代价C4、电压越限惩罚项CU、网损惩罚项Closs、弃负荷惩罚项Cshed和机组无功出力惩罚项CQG：

(7)

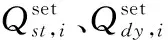
3.2 约束条件

1) 无功补偿容量约束

(8)

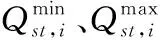
2) 潮流方程约束

以支路mn为分析对象，如图1所示。

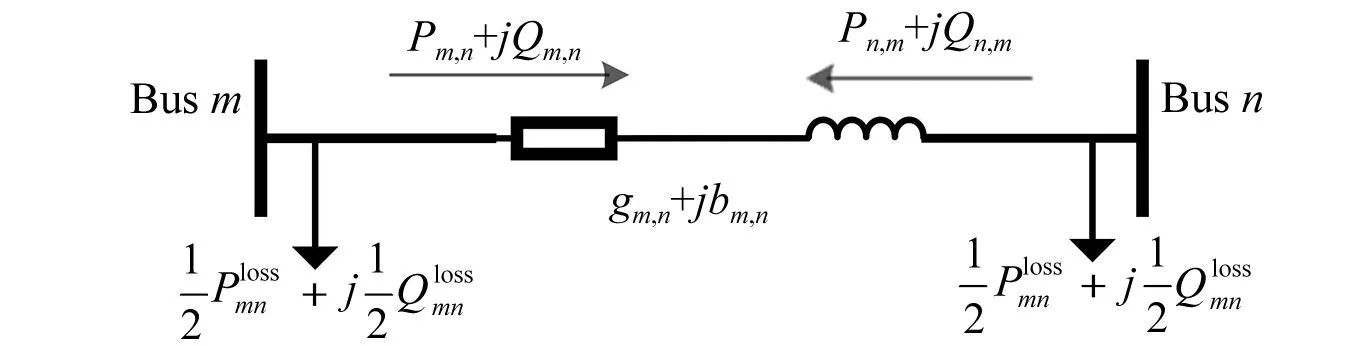
图1 线路潮流示意图

第二阶段的潮流约束采用文献[18]144-145[19]所述的线性化交流潮流方程，如式(9)所示。

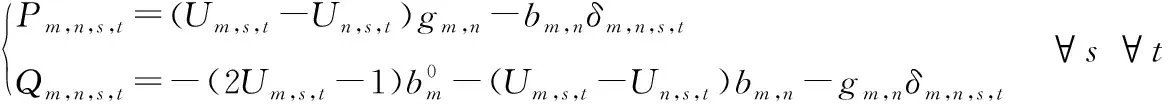
(9)

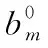
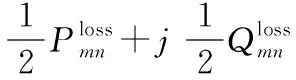
3) 潮流上限约束

(10)

式中：Sm,n,max为支路mn的潮流上限。式(10)为非线性约束，可采用文献[3]1154所述方法进一步线性化。

4) 网损

网损可由式(11)近似表示，可进一步采用文献[18]144-145的线性化方式。

(11)

5) 电力平衡约束

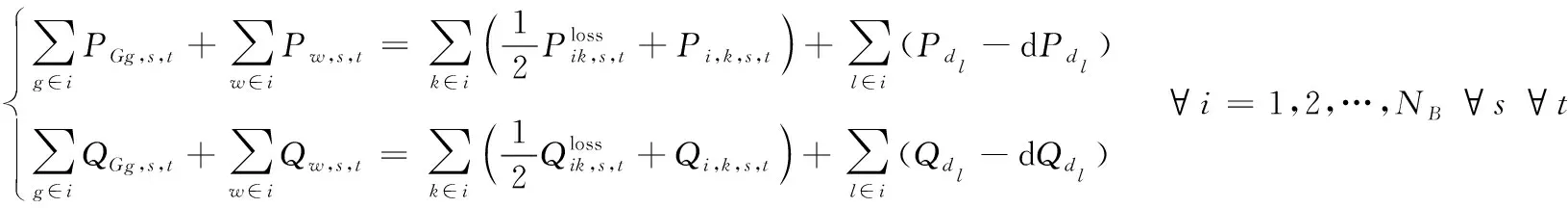
(12)

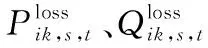
6) 机组出力约束

(13)

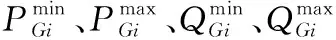
7)机组爬坡约束

(14)

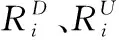
8) 无功投入约束

(15)

4 算例分析

上述模型为混合整数线性优化模型，利用商业求解器可直接求解。采用IEEE 39节电系统在MATLABR2018a平台上进行算例分析[20]。建模工具采用Yalmip工具包，求解器采用Gurobi 9.0.1[21]。

4.1 风电场景及其概率

本文风电场景数取2，最终获取的风电场景如图2所示，概率分别为0.712、0.288。

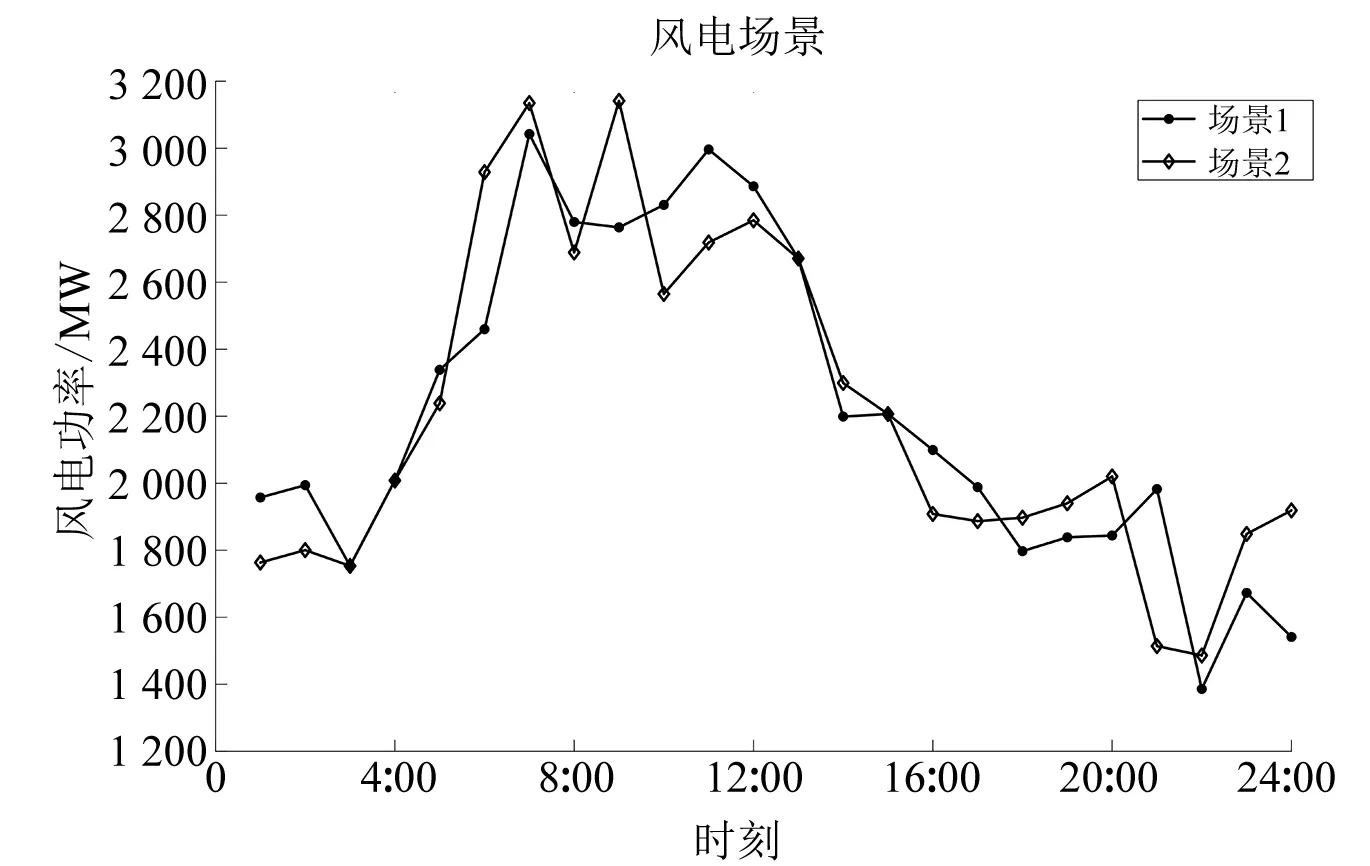
图2 风电场景

4.2 静态电压稳定性与负荷水平的关系

采用如下方法探究系统静态电压稳定性与负荷水平的关系：将case39的有功负荷、机组有功出力同时乘以一系列系数，分别计算L指标值。具体计算结果如图3所示。由此可见，系统负荷水平越高，系统静态电压稳定性越弱，系统越需要通过无功补偿措施提高静态电压稳定性。

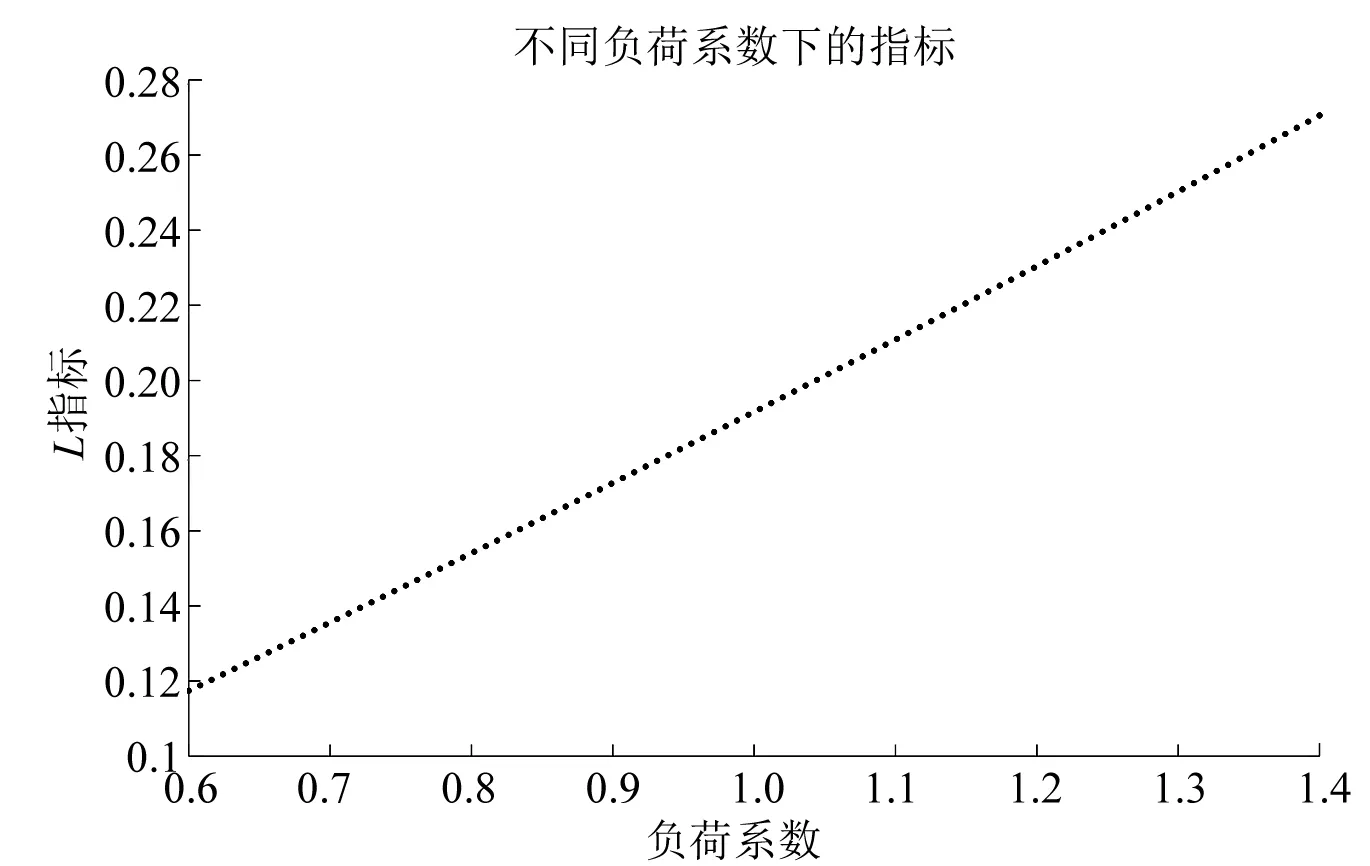
图3 不同负荷水平下系统L指标值

4.3 关键节点与负荷水平的关系

由前文分析可知，各负荷节点L-Q灵敏度指标的计算可以转换为L指标的计算：进行无功补偿后使得系统L指标后下降最多的n个节点为系统关键节点，同时也是无功补偿候选节点，本文n取6。

为探究系统关键节点与负荷水平的关系，仍采用case39，分别在5组不同的负荷水平下(case39的默认负荷乘以负荷系数)计算得到系统关键节点，结果如表1所示。由此可见，在不同负荷水平下，依据该方法选出的系统关键节点是不同的，这对于无功补偿装置的选址会产生较大影响。但考虑到系统的静态电压稳定问题随着负荷水平增大而突出，以高负荷水平下的关键节点作为无功补偿装置候选安装位置。

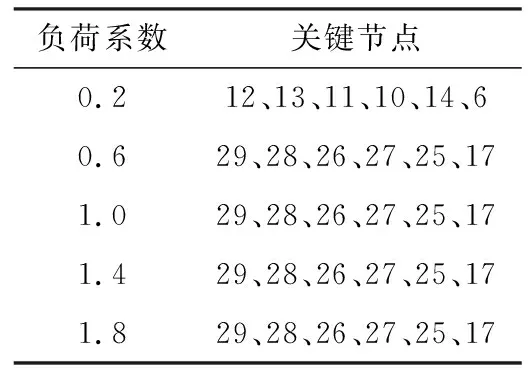
表1 不同负荷水平下求解得到的关键节点

4.4 关键节点有效性分析

为验证候选节点选取的有效性，另外随机选取3组安装节点，各组安装节点均配置50 Mvar的无功补偿容量，计算4组安装方案下的系统L指标。

4组安装方案如表2所示，其中方案0为不进行无功补偿的原系统L指标，方案2、3、4为随机生成的选址方案。

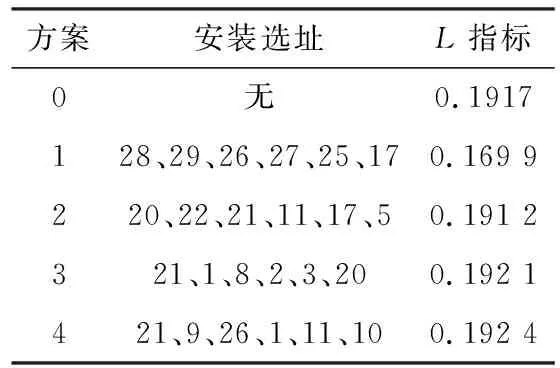
表2 不同无功补偿安装选址对应的L指标

对比方案1和方案2、3、4可以看出，利用L-Q灵敏度指标计算得到的安装地点显著优于随机生成的安装地点。同时对比方案3、4可以看出，不恰当的无功补偿反而会导致系统的静态电压稳定性降低。

4.5 优化算法有效性分析

确定候选安装地点后，还需要确定安装容量以及运行过程中实际投切容量。相关参数参考文献[22]，ast、ady、bst、bdy、cst、cdy、ΔCQ取值分别为20 元/kvar、225 元/kvar、1.2 元/kvar、11.25 元/kvar、6 元/kvar、32 元/kvar、5元/次，考虑的时段为24 h。

系统24 h的负荷曲线如图4所示。整数优化的收敛间隙取0.05%。

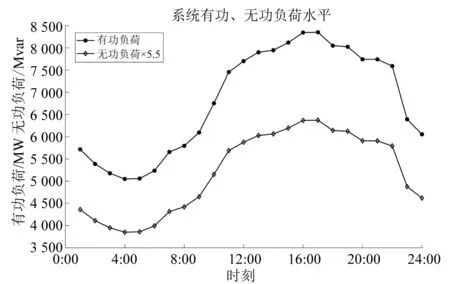
图4 系统负荷曲线

需要说明的是，表3、表4中给出的L指标、电压越限和网损等参数，是各时间段、各节点、各线路求和，然后按照场景概率进行加权的结果。

为验证优化结果的有效性，分别设置两组方案。

方案1：按照前文所述设置目标函数，求得最优解。

方案2：不设置目标函数，求得可行解。

负荷系数取1.2，网损、电压越限和L指标如表3所示。

表3 优化前后系统各项指标对比

由表3可以看出，经过优化之后，系统的各项指标均得到了明显改善。

为验证安装无功补偿装置的必要性，分别设置两组方案：

方案1：无功补偿装置安装档位最大值取10，求得最优解。

方案2：无功补偿装置安装档位最大值取0(即不安装无功补偿装置)，求得最优解。

为了凸显无功补偿的作用，去掉约束条件中的机组有功出力爬坡约束，负荷系数取1.2，网损、电压越限和L指标如表4所示。

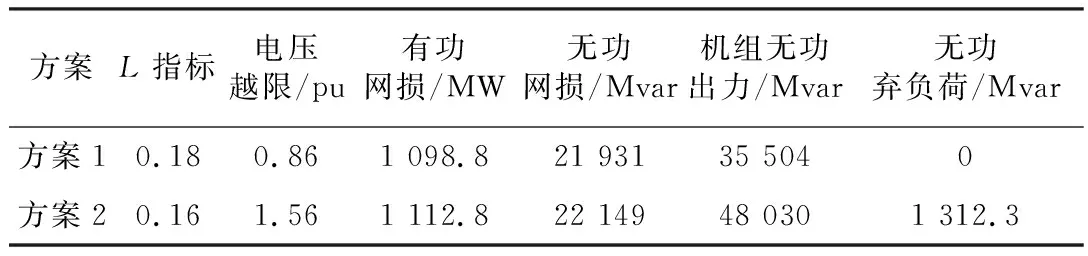
表4 安装无功补偿转置前后系统参数对比

由表4可见，添加无功补偿装置后完全消除了无功弃负荷，同时发电机组的无功出力有了明显减少，可提高发电端功率因数。两种方案的L指标接近，即使方案2供给了更多的无功负荷，但是电压越限以及有功、无功网损在添加无功补偿装置后都有了一定程度改善。

节点电压、有功网损变化曲线如图5、图6所示，进行无功补偿后，系统的各节点电压不仅更加平稳，而且标幺值也更加接近1。同时无功补偿后的网损更低，并且可以看出网损的变化趋势和系统负荷的变化趋势是一致的：负荷越高，网损越高，无功补偿后网损的减小程度越高。

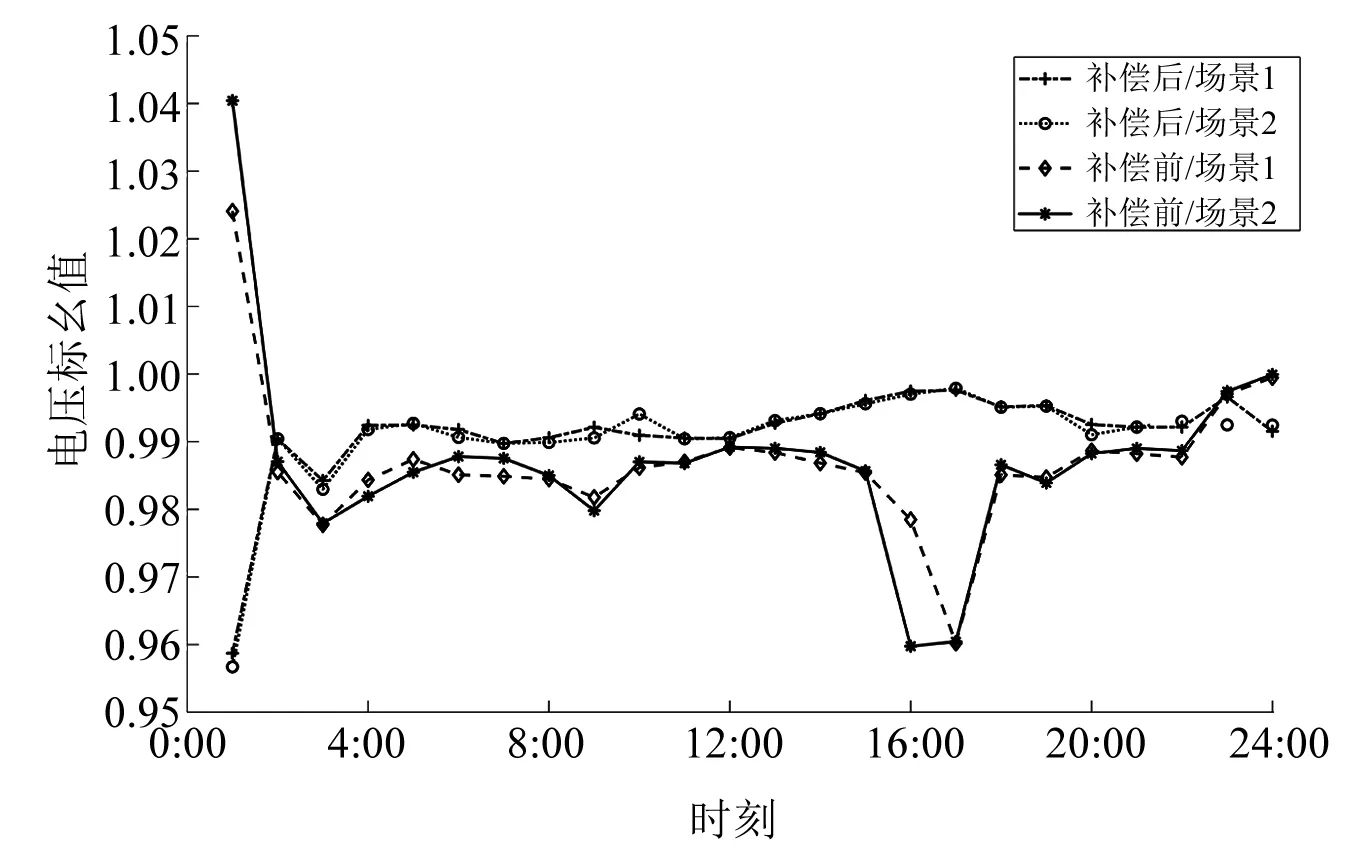
图5 不同场景下无功补偿前后节点电压变化曲线

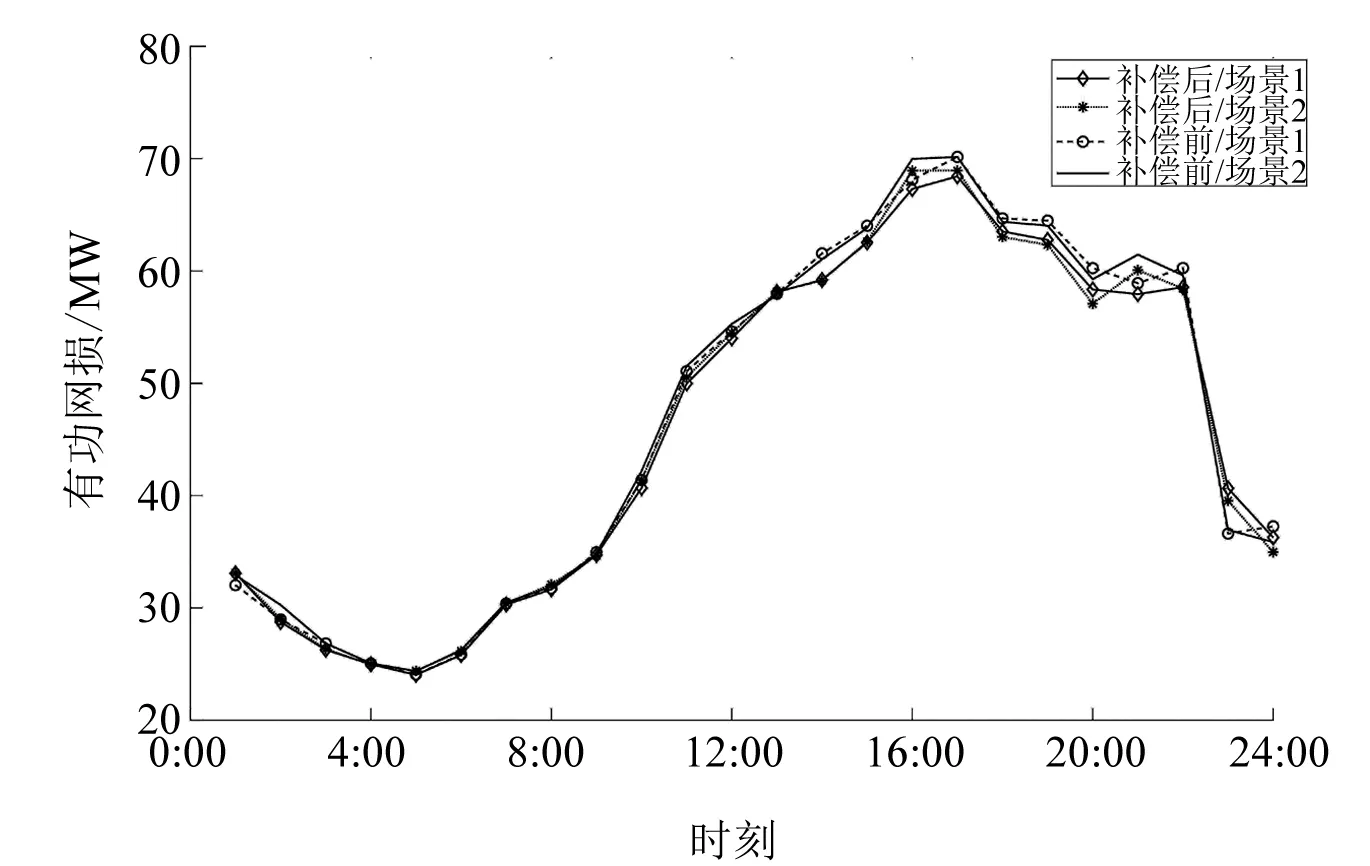
图6 不同场景下无功补偿前后有功网损变化曲线

4.6 无功补偿装置动作情况分析

静态、动态无功补偿设备动作情况如图7所示，需要说明的是，图中数据均为按照场景概率进行加权求和的结果。

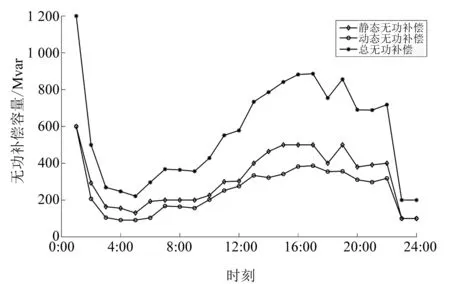
图7 无功补偿装置动作情况

由图7可以看出，补偿容量曲线和系统负荷水平的变化趋势是一致的。其中时刻1的无功补偿容量处于较高水平，主要是由于机组存在无功出力爬坡速率限制，时刻1∶00机组无功出力处于较低水平，为较少无功弃负荷，无功补偿装置大量投入。同时由于静态无功补偿装置的补偿价格更低，除了时刻1∶00(机组无功出力受限)以及时刻23∶00、24∶00(负荷水平较低)，其余时刻静态无功补偿容量均高于动态无功补偿容量。

5 结束语

本文建立了适用于含风电场的电力系统的两阶段无功配置优化模型。经过算例分析得到以下结论：

(1) 系统负荷水平越高，系统静态电压稳定性越弱，系统越需要通过无功补偿措施提高静态电压稳定性。

(2) 不同负荷水平下，通过L指标灵敏度获得的关键节点是不同的，应以高负荷水平下的关键节点作为无功补偿装置候选安装位置。

(3) 利用本文提出的优化模型，可显著提升系统静态电压稳定性，并大幅减小电压越限以及有功、无功网损。同时无功补偿装置的投入可减小发电机组的无功出力，有利于提高发电侧功率因数。

(4) 系统实时运行过程中，网损大小以及无功补偿装置的投入容量的变化趋势都和系统负荷水平的变化趋势具有一致性。