改进型忆阻退化jerk系统初值敏感的动力学和瞬态行为

张春红 ， 朱菊香 ， 张璇

(1.江苏联合职业技术学院 常州铁道分院，江苏 常州 213011；2.南京信息工程大学 滨江学院，江苏 无锡 214105)

0 引 言

忆阻器是一种电阻或电导可调的双端元件，通常包含磁控和荷控两种忆阻器。由于其非线性和记忆性，忆阻器在人工神经网络[1-2]和图像加密[3-4]等领域有着广泛的应用。忆阻器作为非线性元件引入电路之后，混沌电路的动力学行为更为复杂[5]。因此，建立含有忆阻的混沌电路，分析其超级多稳定性的行为，进而阐明非线性系统对于初值的敏感性是十分重要的。

本文在退化jerk系统的基础上，在第二方程中引入理想磁控忆阻器，提出一种改进型忆阻退化jerk系统[6]。新系统具有线平衡点，并表现出含有三种不同拓扑结构混沌吸引子的超级多稳态。此外，通过动力学特性分析，得出改进型忆阻系统的吸引子都是自激吸引子。特别是随着初始条件的变化，新系统表现出瞬态混沌，瞬态周期甚至改变吸引盆和拓扑结构的特殊暂态行为。

1 数学模型与稳定性分析

1.1 数学模型

采用有源磁控忆阻的数学模型为:

(1)

式中:u为忆阻的终端电压；j为忆阻内部磁通变量，j是u的积分；W(j)为与磁通量j相关的磁导率。

在退化jerk系统[6]第二方程中引入式(1)描述的忆阻，即可构建出新颖的忆阻系统，其数学模型表示为:

(2)

式中：x、y、z和w为4个状态变量；a、b和c为原三维系统的3个控制参数。

1.2 稳定性分析

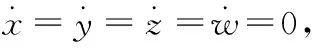
(3)

式中:η为任意实常数。不难看出I1和I2，I3和I4关于y轴对称。

式(2)在平衡点I处的雅克比矩阵为:

(4)

相应的特征方程为：

(5)

除零特征根外，其余的特征根的劳斯阵列表如式(6)所示。

(6)

式中:γ=sgnxIsgnyI(a-1)(α+βη2)/a；μ=sgnxIsgnyI(α+βη2)。

根据劳斯判据为了避免临界稳定状态，系统仅考虑00，两个实正一个实负和一个零特征根。平衡点I2和I3满足sgnxsgny>0，一个实正两个实负和一个零特征根。因此平衡点I1和I4为指数为1的不稳定鞍点，I2和I3为指数为2的不稳定焦点，在I2和I3附近可以形成自激吸引子的两个涡卷。

2 无穷多吸引子的共存行为

2.1 初值敏感的动力学行为

对于式(2)，首先规定控制参数a= 0.6、b= 1.3、c=2、α=1、β=0.03，初始状态[0，0/1，0，w(0)]。当w(0)在(-6, 8)内变化时，系统状态分量x的分岔图及其李雅普诺夫指数如图1(a)和图1(b)所示。随着w(0)的逐渐增大，式(2)表现出复杂动力学行为，包含周期、准周期和不同吸引盆的混沌行为，以及分段倍周期分岔行为等。特别当w(0)∈(-3.697, 4.523)时，式(2)在y(0) = 0和1两个初始条件下，呈现出对x(0)初始条件的敏感性，并且吸引子的混沌行为完全不同。

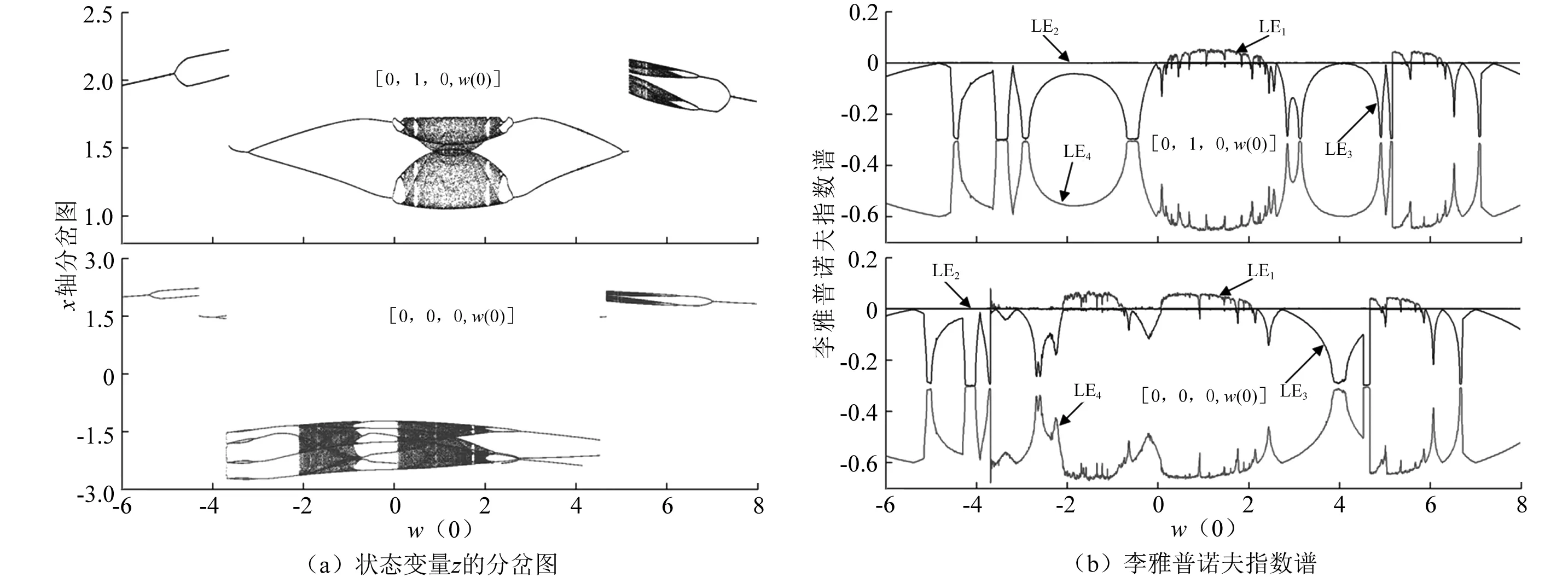
图1 式(2)关于w(0)的动力学

2.2 无穷多吸引子

根据图1的分岔图，仿真获得了在x-z平面上的若干典型吸引子相轨图。这些吸引子有着不同的尺寸和拓扑结构，并且由于忆阻器的引入，式(2)随着初始值的变化，所获得的吸引子的吸引盆也是不同的，因此式(2)存在着超级多稳定性。其中，图2(a)为三种混沌吸引子，图2(b)为准周期和周期。初始状态(0,0,0,0.3)为左，初始状态(0,1,0,1)为中和初始状态(0,1,0,6)为右的三种混沌吸引子。

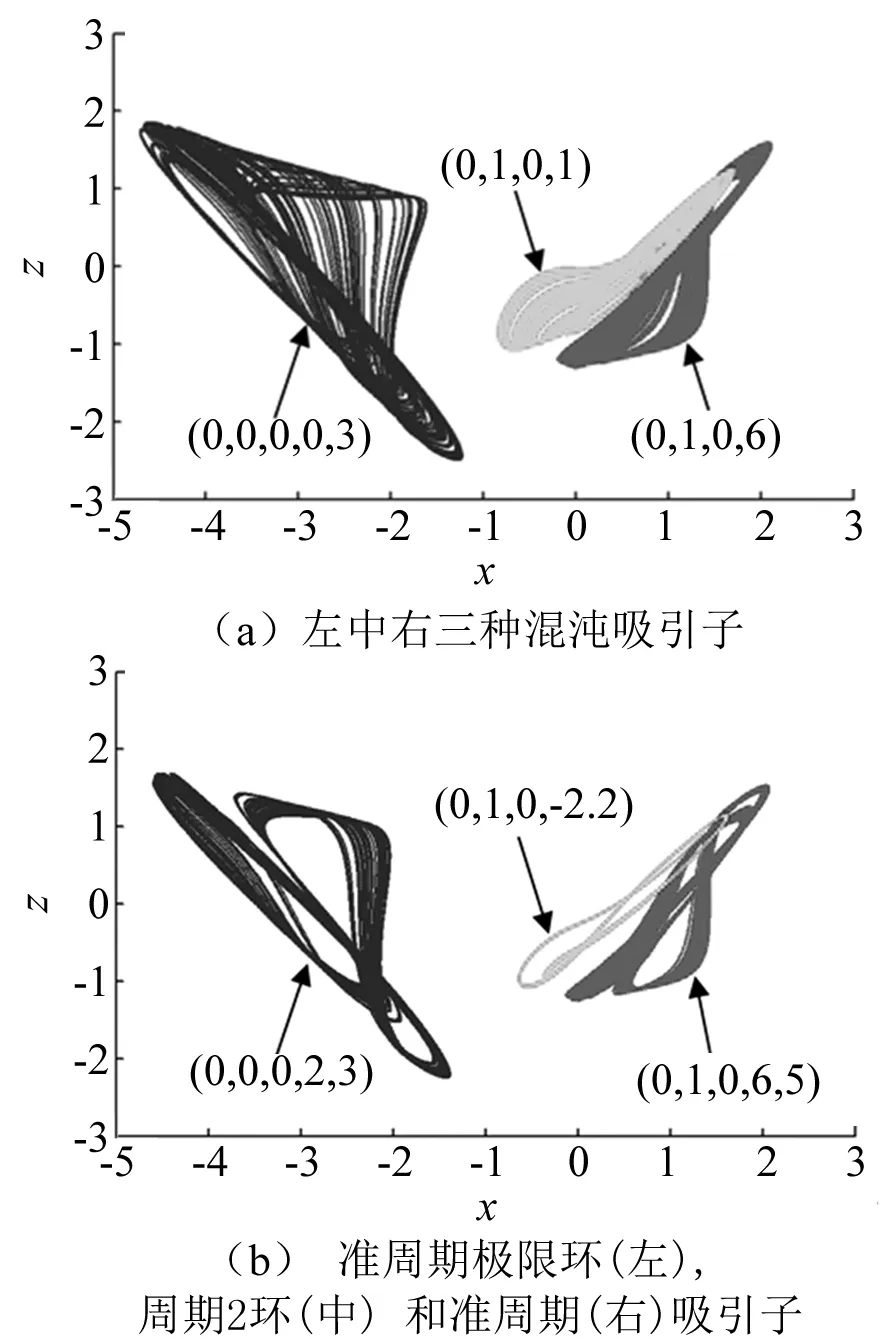
图2 式(2)MATLAB仿真的x-z平面相轨图

3 初值敏感的瞬态行为

对于式(2)，首先规定控制参数a=0.6、b=1.25、c=2、α=0.7、β=0.07，以初始状态 (0，1，0，0)为例，仿真[0.5 ks，0.9 ks]和 [2.5 ks，2.9 ks]两个不同时间段的吸引子相轨图，由一个瞬态周期过渡到稳态混沌。特别以初始状态(0，0，0，-2.3)为例，图3展示了[0.2 ks，0.6 ks]和[0.9 ks，1.3 ks]两个不同时间段的吸引子相轨图，由图3(a)瞬态周期过渡到图3(b)稳态周期。

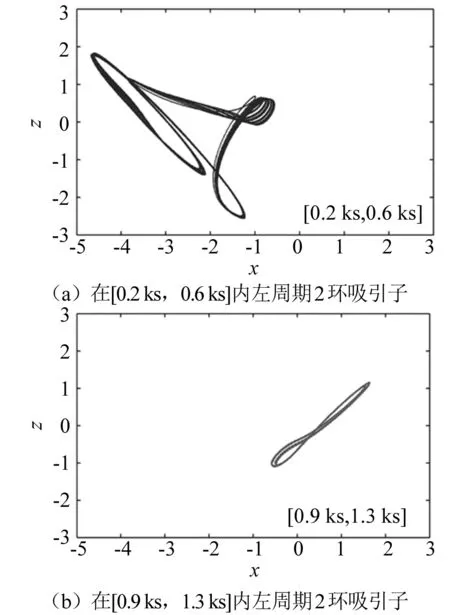
图3 (0,0,0,-2.3)时MATLAB仿真相轨图

4 硬件设计和PSIM仿真

构建忆阻系统式(2)的模拟电路，图4为忆阻jerk系统的主电路。选择时间尺度因子为k=1/(RC)，电路状态方程可以表示为

(7)

式中:ux、uy、uz和uw为电路中 4 个电容两端的电压，分别对应于x、y、z和w状态变量。为了更好地验证系统基于初值敏感存在无穷多吸引子和复杂的瞬态行为，设计了PSIM电路,并进行仿真验证MATLAB数值仿真结果。图4的绝对值函数abs(·)和-abs(·)使用PSIM电路仿真软件中的abs函数模块和比例模块实现。与系统(7)比较，图4中电阻值分别为Ra=R/a=60 kΩ，Rα=R/α，Rβ=gR/β，R1=R4=R=36 kΩ。以图3为例设定电路的初值，验证忆阻退化jerk系统中的复杂现象。由于数学模型与电路模型的时间参数不同，图5中的结果存在一定差异，但两者都显示出基于初值敏感的复杂瞬态动力学行为。

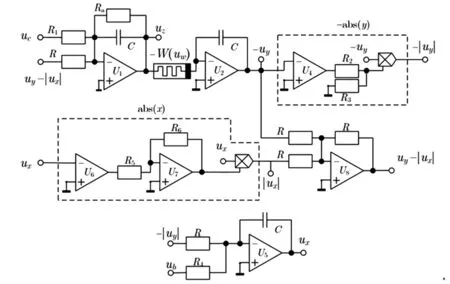
图4 改进型忆阻退化jerk系统主电路

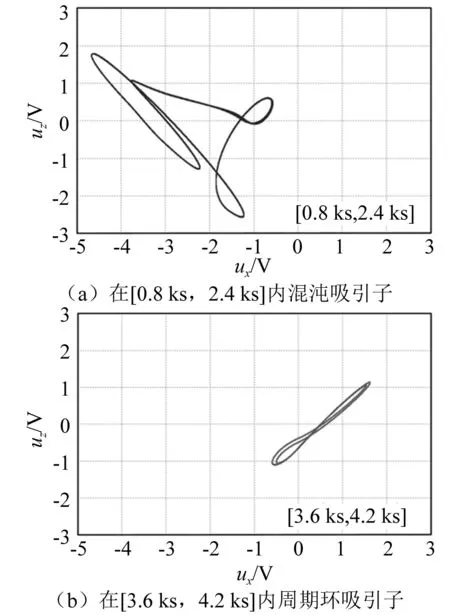
图5 (0,0,0, -2.3)时PSIM模拟的相轨图

5 结束语

通过在退化jerk系统中引入理想磁控忆阻器，提出改进型忆阻退化jerk系统。该忆阻系统固定系统参数条件下，通过改变系统初始状态可以呈现出三种拓扑结构混沌、准周期和周期等超多吸引子共存。调整系统参数后，在不同的初始条件下，改进型退化jerk系统不仅存在瞬态周期和瞬态混沌，还会呈现改变拓扑结构和吸引盆的复杂瞬态混沌现象，呈现对初值敏感的复杂瞬态行为。对系统模型进行模拟电路设计，并通过PSIM电路仿真验证了改进型忆阻退化jerk系统初值敏感的复杂动力学。