基于双层规划模型的光热电站与新能源联合规划

吴源昊， 赵承汉， 李硕， 解大

(1.上海交通大学 电子信息与电气工程学院，上海 200240； 2.上海电机学院 电气学院，上海 201306)

0 引 言

当光热电站作为灵活可控的机组来弥补风电和光伏的波动性出力时，能源间势必具有很强的耦合性[1]。光热电站与新能源电站的联合规划，对制定系统运行控制策略以及实现系统经济运行具有重要意义。

目前研究主要为考虑风电和风光打捆等形式的新能源电站并网的电源规划[2-3]。文献[4]进行了风光沼分布式电源规划。文献[5]考虑风光联合消纳对电源进行规划。而将光热电站纳入待规划电源可以很好地弥补新能源出力的缺陷，改善火电机组的出力特性。此外采用双层规划能更有效地解决两个相互作用和具有不同时间尺度的优化问题，可以更好地实现投资和运行两方面的优化。

本文首先介绍双层规划模型机理，然后对含风-光-火-光热的多能系统进行双层模型规划，通过算例仿真将双层模型与单层模型进行对比，证明了双层模型的先进性。最后对比四种不同电源配置规划方案的方案结果，证明了将光热电站加入待规划电源后经济性、实用性更优。

1 双层规划模型原理

本文建立上层规划层和下层运行层的双层模型。上层规划层模型中，以系统年综合成本作为上层目标函数Fup，以待规划电源的资源容量节点约束和电源接入节点约束作上层函数约束条件g(x)，解得最优的电源接入节点位置和容量；同时建立下层运行层模型，下层目标函数Flow为单个场景下的运行成本，根据上层计算得出的电源位置、容量以及该电源的运行条件作约束条件h(x,y)，求解各电源的出力值，并把计算结果反馈至上层，更新规划层的决策依据，其一般表达式如式(1)所示。

(1)

综上所述，本文的规划思路如图1所示。

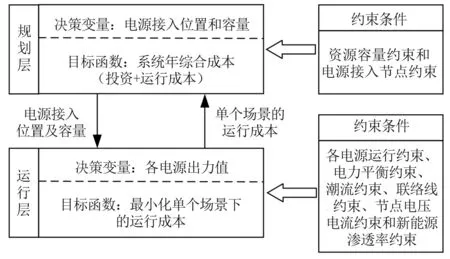
图1 规划思路图

2 含风-光-火-光热的多能协同双层规划

2.1 上层(规划层)模型

2.1.1 目标函数

上层模型的目标函数为：

minFup=C1+C2

(2)

式中：Fup为系统年综合成本；C1为投资成本；C2为运行成本。

2.1.2 约束条件

约束条件如式(3)～式(5)所示。式(3)为风电和光伏的装机容量约束，式(4)为火电机组装机容量约束，式(5)为光热机组装机容量约束。

(3)

(4)

(5)

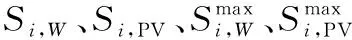
2.2 下层(运行层)模型

下层运行层模型是优化运行模型，可以采用场景内运行成本最小作为调度策略进行建模。下层模型的目标函数如式(6)所示。

minFlow=fo=Cop+Cfuel+Chj

(6)

式中：Flow为最低运行成本；Fo为运行成本；Cop为运维成本；Cfuel为火电机组燃料成本；Chj为火电机组启停成本。此外，下层模型需满足的约束有波动新能源约束、光热电站约束和火电约束等。

2.3 多能协同规划模型求解

双层规划模型属于混合整数非线性模型，为了提高运算效率，可以针对上下层模型采用不同的智能算法进行求解。上层模型属于混合整数非线性模型，采用遗传算法(GA)进行求解；下层模型属于非线性规划模型，采用风驱动优化算法(WDO)进行求解。

本文双层规划模型求解流程如图2所示。

图2 模型求解流程图

图2中：k为本文选取的风光典型场景数；n为当前选择的场景序号。初始化种群，染色体数目为P，其中当前场景下计算的受风驱动的染色体序号为m。

2.4 模型评价指标

为了评价模型及规划方案的优劣，提出以下两个量化指标：

(1) 波动性新能源消纳率。引入新能源消纳率的概念对波动性新能源的消纳效果进行评价，设τ为波动性新能源消纳率，则其值满足如下关系：

(7)

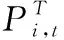
(2) 火电机组调峰比例。定义火电机组调峰比例κ作为评价指标能够体现出光热电站调峰对系统火电机组调峰压力的改善效果，光热电站响应越灵活，κ越小，系统中火电机组出力越平稳。

(8)

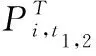
3 算例仿真及分析

光热电站本身具有储热系统，能够实现全天24 h持续出力，在本文作为稳定性电源考虑。

3.1 算例系统介绍

所选迪拜某地区的实际电力系统结构图如图3所示。

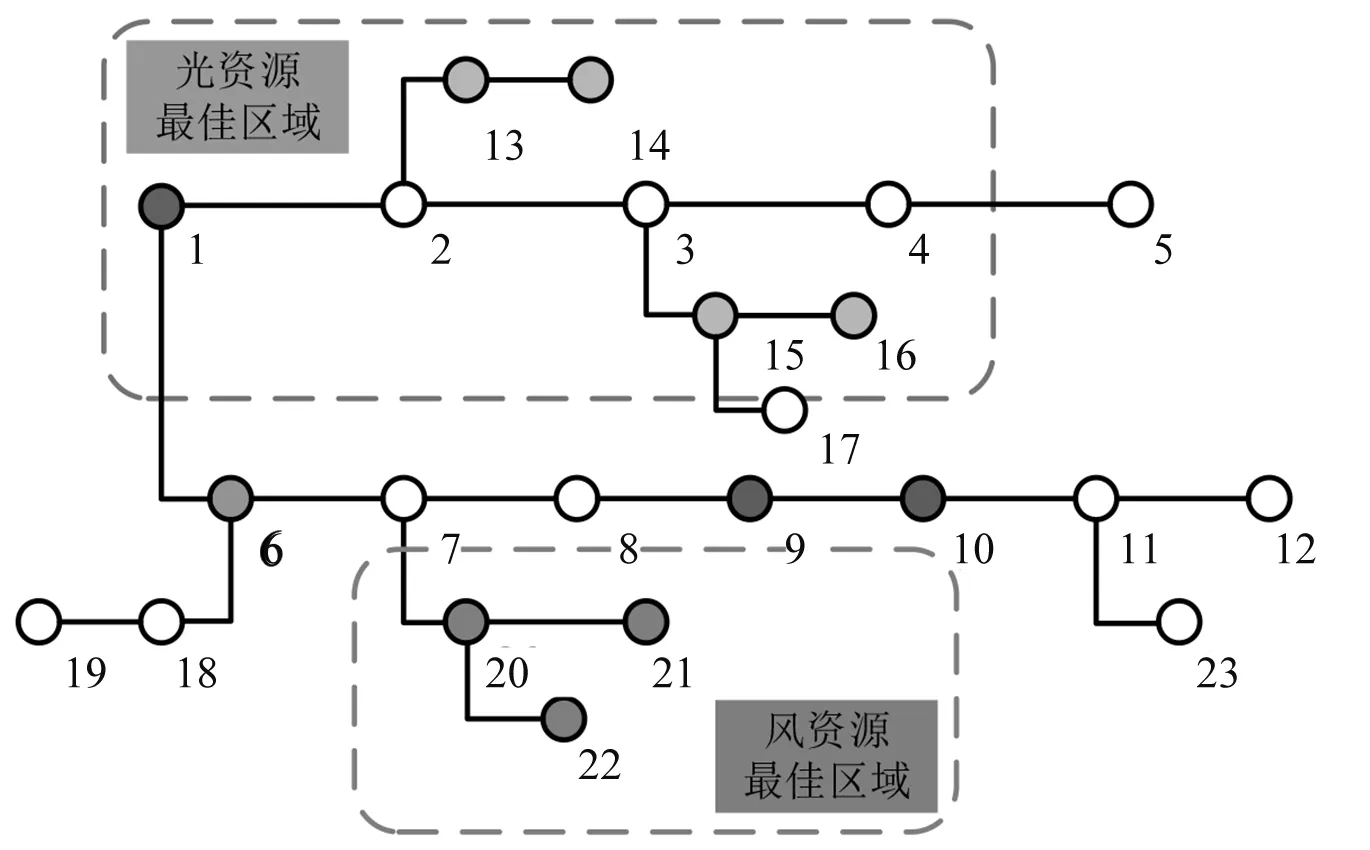
图3 实际算例系统

系统共含有23个节点。该地区地广人稀，根据风光资源分布情况以及各类待选电源的投资成本，设定风电接入节点为20、21、22，光伏接入节点为13、14、15、16，火电接入节点为9、10，光热电站接入节点为1，外送节点为6。

3.2 算例仿真

3.2.1 双层模型先进性验证

为验证提出的双层规划模型的先进性，设置单层典型规划模型作为对比算例。单层规划模型设置如下：

(1)以系统总成本最小为目标函数，决策变量为各接入节点的电源容量，约束条件考虑网络约束与待安装电源的容量约束，与双层规划模型相比未考虑各场景的经济最优运行策略。

(2)与双层模型相同，均采用场景分析理论描述风光不确定性出力，年度总费用为各场景下并行优化运行总费用的期望值，最终的优化结果如表1所示，其中电源规划结果用“接入节点(接入数量)”的形式表示。

表1 不同模型的电源规划结果

由表1可知：单层模型的规划结果中新能源机组占比69.3%，其中波动性新能源装机占总装机容量的64.9%；而双层模型的规划结果中新能源机组占比82.5%，其中波动性新能源装机占总装机容量的73.7%。因此双层模型有效提高了新能源装机渗透率，降低了火电机组的装机比例，装机结构更加清洁化。

如表2所示:与单层模型相比，双层模型年综合费用下降了3.26亿元，年运行费用下降了5.36亿元，火电机组的启停成本与燃料成本分别下降了70.9%%和63.2%。说明双层模型的规划结果在运行过程中减小了火电机组的调峰压力并降低了火电机组的出力，提高了系统的清洁性。

表2 不同模型规划结果的经济性运行结果

3.2.2 规划方案优化验证

本节根据待规划电源的种类提出如表3所示的两种规划方案。

表3 两种方案下的电源规划结果

方案一：待规划电源为风电、光伏和火电。

方案二：待规划电源为风电、光伏、火电和光热电站。

由规划结果对比可知，在均采用双层规划模型的前提下，考虑光热电站作为待规划电源时，波动性新能源的总装机容量提高了13.5%，在更大容量配置风电和光伏装机的前提下，弃风弃光的现象能够得到缓解。

在算例系统中夏季典型日出力场景下，按照双层模型的下层优化运行方式进行对比分析，此时系统的出力运行曲线如图4和图5所示。

图4 方案一夏季典型日出力曲线

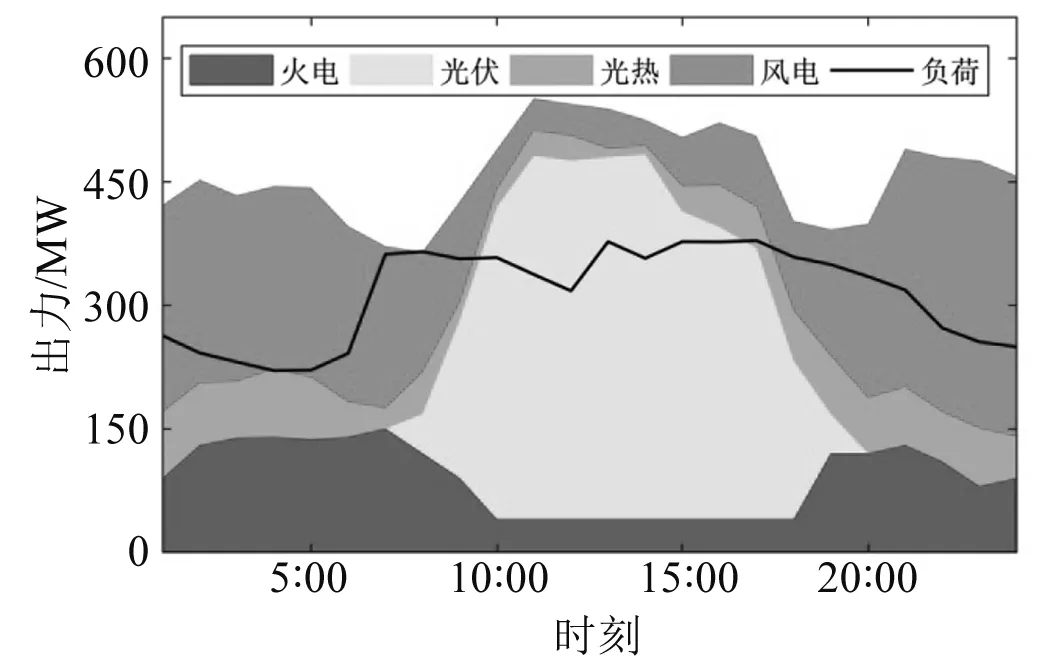
图5 方案二夏季典型日出力曲线

由图4和图5可知，根据下层模型的经济性优化运行策略，方案一即不含有光热电站的规划方案，在实际运行中的波动性新能源消纳率τ=60%，火电机组调峰比例κ=70%；方案二即含有光热电站的规划方案，在实际运行中的波动性新能源消纳率τ=69%，火电机组调峰比例κ=45%。方案一的运行结果中，外送时段主要在0∶00—6∶00，此时风电出力占比最高，达到全天高峰，但是弃风现象明显，本地消纳以火电为主；而方案二基本实现全天24 h外送，其中0∶00—6∶00和19∶00—23∶00由于光热电站的快速响应，减小了火电机组爬坡和弃风量，本地消纳以清洁能源为主，全天24 h外送电量明显大于方案一。

综上所述，在规划阶段考虑光热电站作为待规划电源能够有效地提高波动性新能源的消纳量，同时减小火电机组出力，提高系统清洁能源比例。

4 结束语

本文提出了考虑光热电站和波动性新能源作为待规划电源的电源双层规划模型，并从规划和运行的角度求解规划方案实现经济最优，主要研究结论如下：

(1)双层模型与单层模型相比，其下层考虑了各场景实际运行成本最小作为运行策略，在运算过程中通过上下层的迭代获得最终的规划方案，结果能够满足上层规划和下层运行不同时间尺度的经济性最优。

(2)仿真结果表明，在规划阶段考虑光热电站作为待规划电源能够有效地提高风电和光伏的消纳，同时减小火电机组出力，提高系统清洁能源比例，减少火电机组爬坡，减轻火电机组调峰压力。