基于CRITIC加权和IMFO-LSSVM的光伏发电功率短期预测

林鹏， 于洋， 张昕， 谢震伟， 张家豪， 王昕

(1.上海交通大学 电工与电子技术中心，上海 200240；2.国网吉林省电力有限公司延边供电公司，吉林 延边 133000)

0 引 言

光伏发电利用太阳能可再生的特点，可以缓解目前的能源危机问题[1]。但是光伏发电具有较大的随机性和间歇性[2-3]，若能准确地预测光伏发电功率，对电网的安全稳定运行意义重大。目前许多学者利用机器学习算法结合历史气象信息对光伏发电功率进行预测。文献[4]采用经验分解法与LSSVM相结合的预测方法，但是该方法没有对最小二乘支持向量机(least squares support vector machine,LSSVM)的参数进行优化。文献[5]搭建基于相似日与改进思维进化算法优化径向基神经网络的光伏功率预测模型。文献[6]利用PVPNet深度神经网络模型结合气象因素对光伏出力进行预测，但是这两种方法得到的预测精度都较低。

为了提高光伏发电功率预测的精度，本文提出了一种利用CRITIC加权灰色关联度提取相似日的改进飞蛾扑火算法(improved moth-flame optimization algorithm,IMFO)优化LSSVM的光伏发电功率短期预测方法。该方法首先在同类天气状况下利用CRITIC加权灰色关联度提取相似日，由于对各气象因素赋予了客观权重，提高了相似日选取的优异度。然后，利用柯西变异和自适应权重对传统的飞蛾扑火算法(moth-flame optimization algorithm ,MFO)进行改进，增强了MFO的寻优能力。最后，搭建基于IMFO优化LSSVM的预测模型，并利用澳大利亚某光伏电站的数据进行预测，证明本方法的优越性。本文研究为光伏发电功率预测方面的研究提供了一定的指导意义。

1 相似日提取

1.1 光伏发电影响因素分析

本文选取澳大利亚DKASC某光伏电站的数据样本进行分析。将数据进行无量纲化处理，绘制出2017年12月9日光伏发电功率与温度、湿度、直接辐射强度和漫射辐射强度的关系，如图1所示。

由图1可知，该日的功率输出与温度、水平辐射度和漫射辐射度有很强的正相关性，而与湿度有负相关性。为了研究各因素之间相关性大小，引入pearson相关系数ρ进行分析，其计算公式为:

图1 光伏功率与各气象因素归一化结果

(1)

通过式(1)计算出所选择样本数据晴天天气状况下功率与温度、湿度、水平辐射度和漫射辐射度的相关性，分别为0.198、-0.229、0.857、0.348。可知水平辐射度与功率的正相关性最强，其次为漫射辐射度和温度，而湿度与功率的输出呈负相关。因此，可以根据各气象因素对光伏输出功率的相关性不同，在相似日提取过程中计算各气象因素的权重。

1.2 加权灰色关联度提取相似日

1.2.1 灰色关联度

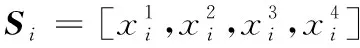
(2)

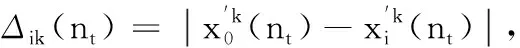
(3)

1.2.2 CRITIC方法

CRITIC方法是一种客观赋权的方法，求取各气象因素对光伏发电功率输出的客观权重是以各气象因素指标内数据的对比强度和冲突性来综合衡量的。

设Ck为第k个气象因素所包含的信息量，Ck的计算式为:

(4)

式中:σk为第k个气象因素的标准差;ρkv为气象因素k与气象因素v之间的相关系数。第k个气象因素的客观权重ωk的计算式为:

(5)

将式(5)代入到式(3)中，即可获得历史日与待预测日的加权灰色关联度。

2 预测模型搭建

2.1 LSSVM

对于给定的训练集{xj,yj}，xj∈Rm为输入，m为Rm空间的维数，yj∈R为输出，j=1,2,…,N，N为训练样本集个数。当LSSVM用于回归预测时，预测模型输出y的计算式为[7]:

(6)

式中:θ为核参数;b为偏移量;αj为包含正则化参数η的函数。

2.2 改进的飞蛾扑火算法

2.2.1 飞蛾扑火算法

在飞蛾扑火算法中首先假设候选解是飞蛾，把飞蛾在空间中的位置作为问题的变量，飞蛾通过飞行改变其在空间中的位置寻找最优解。飞蛾的集合用矩阵U为:

(7)

式中:n为飞蛾的数量;d为变量的维度。用矩阵OU=[OU1,OU2,…,OUn]T存储飞蛾适应度值，适应度值可以通过当前飞蛾的位置代入适应度函数获得，每代飞蛾可以按照适应度值大小进行排序作为下一代火焰。

每只飞蛾通过与之对应的火焰更新其位置，火焰的维度与飞蛾的维度相同。火焰的集合用矩阵H为:

(8)

同样，也有一个适应度值矩阵OH=[OH1,OH2,…,OHn]T与矩阵H对应，用来存储火焰当前适应度值。飞蛾通过不断地在火焰周围进行迭代寻优得到最优解。飞蛾相对火焰更新的计算式为：

Un=S(Un,Hm)

(9)

式中:Un为第n只飞蛾;Hm为第m个火焰；S为对数螺旋函数。S的计算式为:

S(Un,Hm)=D′eBtcos(2πt)+Hm

(10)

式中:D′=|Hm-Un|为第n只飞蛾与第m个火焰的距离;B为对数螺旋函数的形状参数;t为[-1,1]间的随机数。由飞蛾的更新公式可知，下一代飞蛾的位置与当前火焰的位置有关。通过不断迭代更新当前飞蛾位置进行寻优，满足要求后寻优结束。

2.2.2 改进飞蛾扑火算法

为了平衡全局搜索和局部搜索能力，引入柯西变异来提高飞蛾扑火算法的全局搜索能力，引入自适应权重来提高飞蛾扑火算法的局部搜索能力。

1) 柯西变异

引入柯西变异可以增加种群的多样性，避免算法陷入局部最优，其对当前最优解X更新的计算式为:

(11)

式中:X′为更新后的解；z为服从柯西分布的随机数。该算法在执行过程中，如果使用柯西变异后，适应度值比未变异之前更优，则用此时的解替代原来的解，否则原解保持不变。

2) 自适应权重

为了提高算法的局部搜索能力引入自适应权重ωsa，计算式为:

(12)

式中:Tc为当前迭代次数;Tmax为最大迭代次数;∂为比例系数，在本文中∂为1。那么，改进后的飞蛾相对火焰更新的计算式为

S(Un,Hm)=D′eBtcos(2πt)+ωsaHm

(13)

由式(13)可知，在迭代寻优过程中，随着迭代次数的增加，ωsa自适应地减小。这样，在初始时梯度下降比较快，当飞蛾接近火焰时，梯度下降比较慢，这样能够提高飞蛾的局部搜索能力。

2.3 IMFO算法优化LSSVM模型

LSSVM中正则化参数 和核参数对预测精度影响很大，利用IMFO算法对这两个参数进行寻优。在测试验证过程中利用此时具有最优参数的LSSVM模型进行预测能够提高预测精度。IMFO优化LSSVM模型的具体步骤如下：

步骤1：分别在晴、多云和雨三种天气类型下随机选取某一天作为测试样本，测试样本作为待预测日，余下的样本作为当前的训练样本。利用CRITIC方法确定各气象因素的权重，根据加权灰色关联度提取与待预测日相似度最高的5 d作为新的训练样本，此步骤为数据预处理步骤。

步骤2：参数初始化，主要是设定最大迭代次数Tmax，初始飞蛾种群数量n，变量维度d，飞蛾的搜索空间等，在本文中设置初始飞蛾种群数量为20，最大迭代次数为100，变量维度为2,飞蛾在两个维度的搜索空间均为[0.01 2 000]。

步骤3：初始化飞蛾的位置U，即在多维空间中随机生成飞蛾的位置。

步骤4：根据步骤1得到的新的训练样本，利用步骤3初始化的飞蛾位置作为正则化参数η和核参数θ的当前值，并利用LSSVM模型计算当前的适应度，将适应度值存储在OU中，适应度值为预测结果的均方根误差。

步骤5：适应度值OU按照逐渐增大的顺序进行排序，飞蛾根据适应度值的位置进行重新排序，并将排序后的结果赋给火焰H，并计算当前火焰的适应度值OH。

步骤6：根据式(13)螺旋更新飞蛾相对于火焰的位置，然后根据加权灰色关联度提取的相似日作为训练样本，利用LSSVM模型计算当前的适应度值，并将当前解进行柯西变异，根据变异前后的适应度值的大小，选取当前最优解。然后，飞蛾位置和火焰位置根据步骤5重新排序。

步骤7：如果满足终止条件，则程序停止运行并将最优结果输出，否则返回步骤6重新运行程序。

步骤8：将此时具有最优参数的LSSVM模型用来预测，将测试样本的气象因素作为输入，用来预测输出功率。

3 实例分析

3.1 数据来源

本文中所用的光伏数据集来自澳大利亚DKASC某光伏电站，时间为2017年12月1日至2018年2月15日7∶00—19∶00，共计77 d 数据样本。数据集包含功率、温度、湿度、水平辐射度和漫射辐射度。将所选样本分为晴天、多云和雨天，其中晴天45 d，多云20 d，雨天12 d。

3.2 评价指标

本文采用平均绝对误差rMAE，均方根误差rRMSE作为评价指标，rMAE、rRMSE的计算式分别为:

(14)

(15)

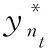
3.3 预测结果

根据本文的理论基础和光伏数据集，搭建预测模型进行验证，运行环境为MATLAB 2018a，调用LSSVMlab1.8工具箱对LSSVM中正则化参数和核参数进行寻优，工具箱中其他参数保持默认设置。在晴天、多云和雨天分别随机选取1 d 进行预测。利用未加权灰色关联度提取相似日的MFO优化LSSVM(未加权MFO-LSSVM)预测模型，CRITIC加权灰色关联度提取相似日的MFO优化LSSVM(加权MFO-LSSVM)预测模型，CRITIC加权灰色关联度提取相似日的IMFO优化LSSVM(加权IMFO-LSSVM)预测模型进行预测，并将结果对比。晴天、多云和雨天利用上述预测模型得到的光伏输出功率变化分别如图2～图4所示。

图2 晴天光伏功率预测结果

图3 多云天光伏功率预测结果

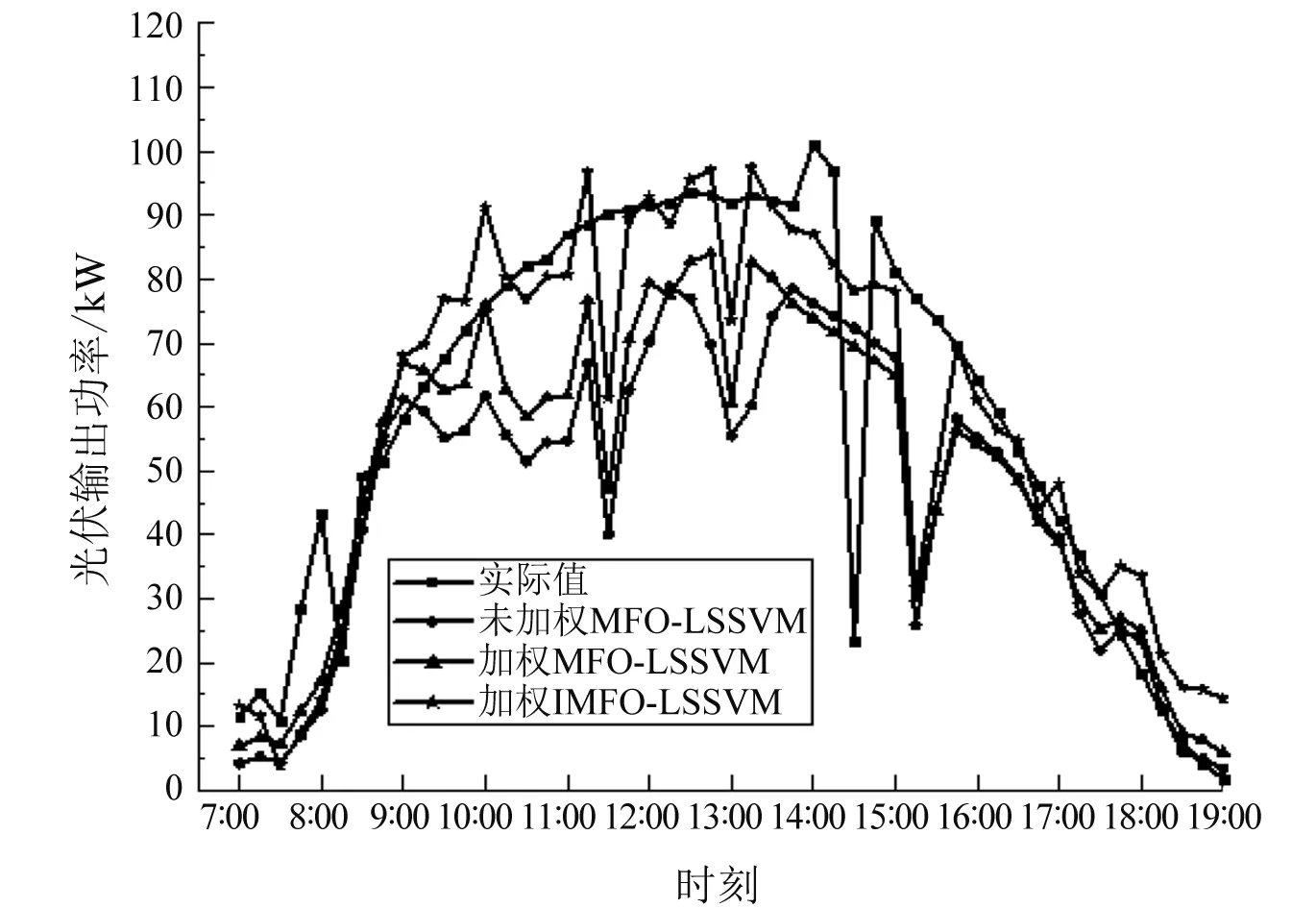
图4 雨天光伏功率预测结果

为了进一步分析各种方法的精度采用平均绝对误差rMAE和均方根误差rRMSE进行分析。表1为不同天气状况下预测结果的评价指标。从表1可以看出，利用加权MFO-LSSVM预测模型相较于未加权MFO-LSSVM预测模型在晴天、多云和雨天时平均绝对误差分别降低了0.24、2.47和2.73，均方根误差分别降低了0.19、2.90和3.24。这是由于未加权MFO-LSSVM预测模型在进行相似日提取时各气象因素对光伏输出的影响权重相同，这样不利于寻找最优相似日样本。加权MFO-LSSVM预测模型在提取相似日的过程中采用了CRITIC加权灰色关联度，赋予各气象因素不同的客观权重，提高了相似日选取的优异度，因此其预测精度更高。

表1 不同预测方法下的rMAE和rRMSE

对比加权IMFO-LSSVM预测模型和加权MFO-LSSVM预测模型可以发现，前者在晴天、多云和雨天时平均绝对误差分别降低了0.21、3.53和4.16，均方根误差分别降低了0.08、2.17和3.39。这是由于加权IMFO-LSSVM预测模型相较于加权MFO-LSSVM预测模型对飞蛾扑火算法进行了改进，由于传统的飞蛾扑火算法容易陷入局部最优，利用柯西变异和自适应权重分别增强了飞蛾扑火算法的全局搜索能力和局部搜索能力，这样能够得到更优的正则化参数η和核参数θ，因此加权IMFO-LSSVM预测模型得到的预测精度更高。综上可以看出无论是在晴天、多云还是雨天，加权IMFO-LSSVM光伏发电功率预测模型比其他预测模型得到的预测精度更好。

4 结束语

本文利用CRITIC加权灰色关联度提取相似日与IMFO优化LSSVM的预测模型对光伏发电功率进行了研究。通过CRITIC加权灰色关联度提高了相似日选择的优异度，通过自适应权重和柯西变异增强了传统飞蛾扑火算法的寻优能力，所得结果相对其他方法预测精度较高。本文的研究可以为光伏发电功率预测的研究提供一定的指导意义。