火灾作用后钢管混凝土构件侧向撞击性能研究
纪孙航, 史艳莉, 王文达
(兰州理工大学 土木工程学院,兰州 730050)
钢管混凝土不仅具有优越的力学性能和良好的施工性能,与钢结构相比,钢管混凝土由于钢管与混凝土之间的互补作用使得其具有良好的耐火性能和火灾后修复性能[1]。该类构件被广泛应用于高层及超高层结构、大跨结构、桥梁结构和交通枢纽站台等结构或构筑物中[2]。在结构服役过程中,除需要面临常规荷载外,往往面临着火灾、地震和撞击等荷载的威胁。自2001年“9·11”事件后,结构或构件等在火灾、爆炸和撞击等荷载作用下性能引起广泛关注和研究。
钢管混凝土结构在服役期间不可避免地可能会遭受撞击荷载,如结构倒塌造成的冲击,交通工具对站台柱等的撞击,恐怖袭击造成的冲击等。目前关于钢管混凝土构件的侧向撞击性能研究较多。Wang等[3-5]均对钢管混凝土构件进行了侧向撞击试验,结果表明钢管混凝土具有良好的抗侧向撞击性能。Wang等[6-9]对不同截面形式的钢管混凝土组合构件进行了侧向撞击性能研究。Zhao等[10-11]对不锈钢管混凝土组合构件进行了侧向撞击性能研究,结果表明该类组合构件的抗撞击性能优于普通钢管混凝土。
火灾往往会造成巨大的损失,严重威胁人类的生命和财产安全,随着现代建筑结构的高层化和功能复杂化,建筑火灾的问题也日益严峻。钢管混凝土结构在遭受火灾后往往面临着修复问题,需要对结构火灾后的性能做出评估。因此除钢管混凝土结构的耐火性能外,对其火灾作用后的性能进行研究也十分必要。Han等[12-13]先后对标准火灾作用后不同截面形式的钢管混凝土柱进行了火灾后剩余承载力试验,并在参数分析的基础上给出构件剩余承载力的计算方法。林晓康等[14-15]对火灾作用后的钢管混凝土和中空夹层钢管混凝土构件进行了滞回试验研究。受火后的钢管混凝土构件在使用过程中也可能遭受撞击荷载,因此有必要对其抗撞击性能进行研究。任晓虎等[16]对高温作用后钢管混凝土短柱进行轴向撞击试验,结果表明高温作用后的钢管混凝土仍具有良好的抗轴向撞击性能和完整性。目前关于钢管混凝土火灾作用后基本力学性能的研究较多,对该类构件在火灾作用后的侧向撞击性能研究极少。
为此,本文建立了火灾作用后钢管混凝土构件的侧向撞击数值模型,分别对已有火灾作用后钢管混凝土构件的压弯试验和常温下的钢管混凝土侧向撞击试验进行模拟,以验证本文模型的准确性。比较了不同受火时间后构件的挠度、撞击力和截面弯矩的时程曲线,以及受火后构件的弯矩和剪力分布形态。通过吸能系数、截面动态极限弯矩和火灾后动态弯矩提高系数对火灾作用后构件的抗撞击性能进行量化分析,并基于“塑性铰”简化模型,给出火灾作用后构件跨中最大挠度计算公式。
1 有限元模型
1.1 钢材的本构关系模型
温度对钢材的性能影响明显,高温下钢材强度显著降低,但当受火钢材的温度降至常温后,钢材的力学性能有所恢复。本文高温作用后的钢材采用双线性模型,其应力(σ)-应变(ε)关系式为
(1)
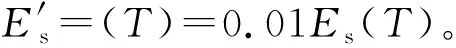
(2)
与静态荷载相比,动态荷载作用下钢材强度明显提高,其应变率效应不可忽略。采用Cowper-Symonds模型考虑钢材在不同应变率下的动态屈服强度,具体表达式为
(3)
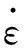
1.2 混凝土的本构关系模型
混凝土采用塑性损伤模型,高温作用后圆钢管混凝土中核心混凝土采用韩林海研究中建议的应力-应变关系模型,具体表达式为
(4)
式中:ξ为约束效应系数;β与q为参数;x=ε/εo;y=σ/σo,σo和εo为考虑了温度影响修正后的混凝土极限应力和极限应变,具体确定方法见韩林海的研究。
动态荷载作用下混凝土的应变率效应明显,目前多采用CEB-FIP中的模型考虑混凝土抗压强度提高的现象,具体表达式如式(5)所示。由于火灾作用后混凝土温度恢复至常温,且目前没有关于火灾作用后混凝土动态强度模型的研究,故本文采用式(5)计算混凝土的动态抗压强度
(5)
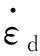
1.3 构件的尺寸与边界
在ABAQUS/standard中建立构件的温度场模型,采用ISO-834标准升温曲线作为构件的升温模型,构件受火均匀,通过瞬态热传递完成构件的温度场分析。在ABAQUS/Explicit中建立构件的动态撞击模型,构件的钢管和混凝土网格尺寸与温度场模型保持一致,以便将温度场的分析结果作为初始状态导入撞击模型中。构件长度为1 200 mm,截面直径为120 mm,钢管壁厚为3 mm,钢材屈服强度为345 MPa,混凝土抗压强度为50 MPa,落锤宽度为30 mm。当落锤质量和撞击速度选取合适时才能获得完整的撞击力时程曲线,参考已有常温下钢管混凝土的侧向撞击试验的质量和速度取值,经多次试算与调整,最终确定落锤质量为240 kg,撞击速度为6 m/s。构件的边界条件与网格划分,如图1所示。落锤的位置定义在构件上表面1 mm处,并赋予落锤质量和初始速度。落锤与钢管采用“硬接触”,钢管与混凝土之间法向采用“硬接触”,切向采用“面面接触”。内外钢管的网格划分保持一致,网格大小为15 mm。
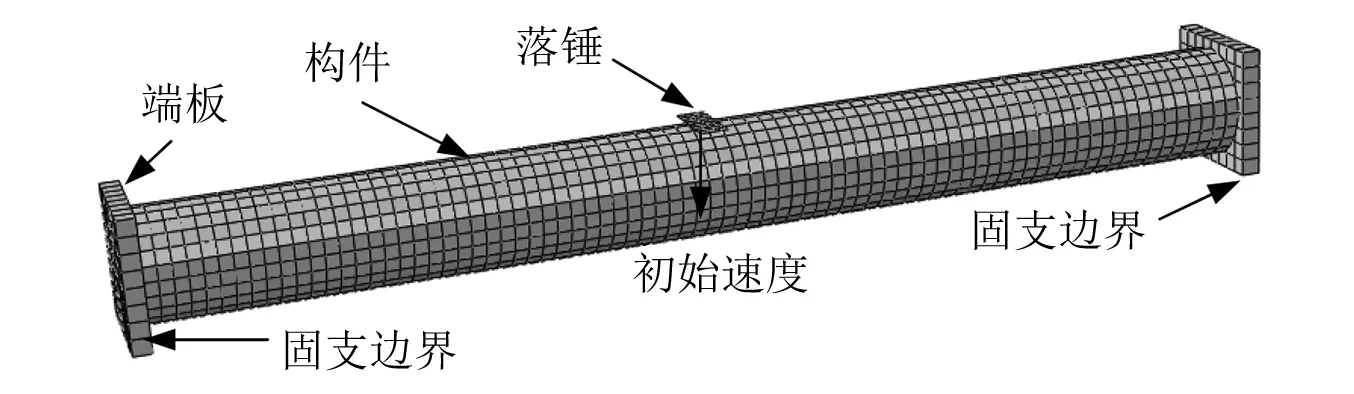
图1 边界条件与网格划分Fig.1 Boundary conditions and element division
2 模型验证
由于目前没有钢管混凝土构件在火灾作用后的侧向撞击试验,为验证本文模拟方法的合理性与准确性,分别对已有的火灾作用后钢管混凝土构件的压弯试验和常温下的钢管混凝土侧向撞击试验进行数值模拟。
2.1 钢管混凝土构件火灾作用后模型验证
火灾作用下钢材的强度随着温度升高逐渐降低,但当温度降为常温后,钢材强度有所恢复,而混凝土的材性只与经历的历史最高温有关。火灾作用后钢管混凝土数值模拟的关键是构件经历的温度与其不同温度材性对应的准确性。因此,为验证火灾作用后数值模拟方法的准确性,对火灾作用后圆钢管混凝土柱剩余承载力试验进行模拟。火灾作用后试件试验信息如表1所示,试件截面直径为108 mm,钢管壁厚为4.32 mm。表中:L为试件长度;e为荷载偏心距;to为受火时间;Nt为实测的火灾后剩余承载力值;Np为模拟火灾后剩余承载力值。
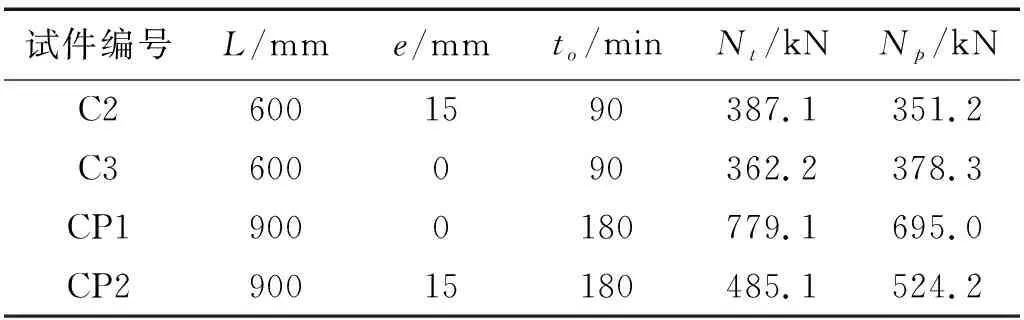
表1 火灾后试件试验信息表Tab.1 Information of tested post-fire specimens
试件试验荷载-位移曲线与模拟曲线的对比情况,如图2所示。模拟火灾后剩余承载力值与实测值之比的平均值为0.98,均方差为0.083,可见,模拟结果与试验结果吻合良好,说明火灾作用后钢管混凝土构件模拟方法准确。
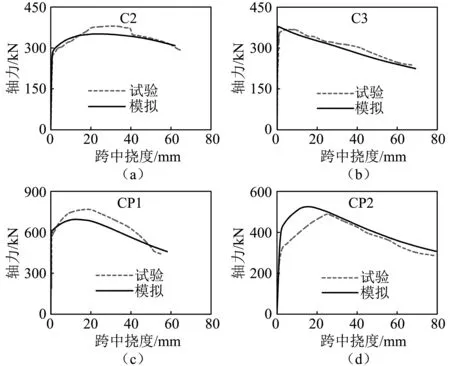
图2 荷载-挠度曲线模拟与试验结果对比Fig.2 Comparison between predicted and experimental load versus deflection curves
2.2 常温下钢管混凝土侧向撞击试验模拟
为验证钢管混凝土构件在侧向撞击荷载作用下模拟方法的准确性,对已有钢管混凝土侧向撞击试验[17]进行数值模拟,试件具体信息如表2所示,试件长度均为1 200 mm,钢管截面直径均为114 mm。表中,ts为钢管壁厚,H为落锤高度,vo为落锤速度。
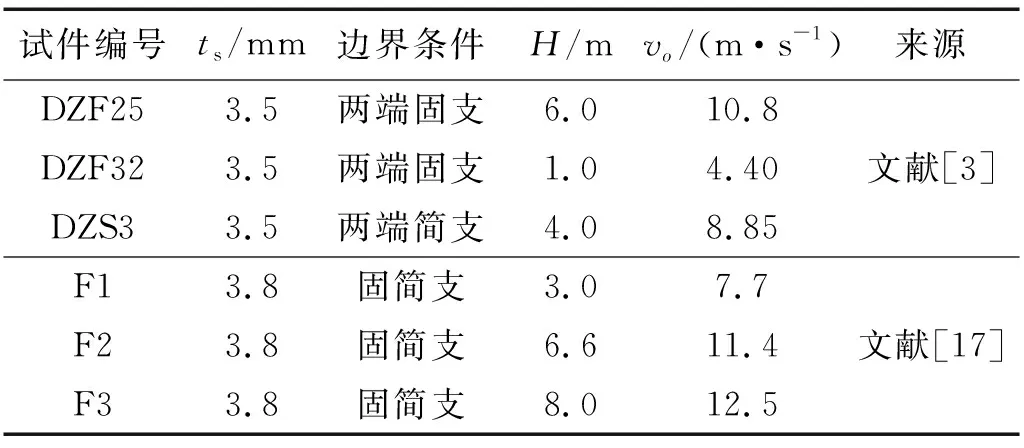
表2 试件信息表Tab.2 Information of tested specimens
图3给出试件典型的模拟撞击力时程曲线与试验曲线对比情况。可以看出,模拟的撞击力时程曲线与试验曲线整体吻合良好,试件的撞击力时程曲线均有明显的平阶段,可分为峰值阶段、平台阶段和卸载阶段。图4为试件的模拟结果与试验结果的对比情况,撞击力平台值、跨中挠度和撞击时程模拟结果与试验结果之比的平均值分别为1.03,1.08和0.99,其均方差分别为0.099,0.092和0.063。可见,模拟结果与试验结果吻合良好,说明钢管混凝土构件的侧向撞击模拟方法合理准确。
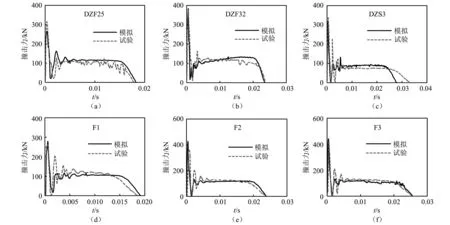
图3 模拟撞击力时程曲线与试验曲线对比Fig.3 Comparison between tested and calculated timehistory curves of impact force
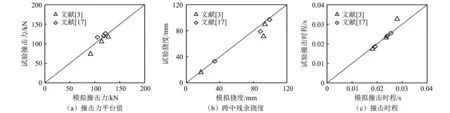
图4 模拟结果与实测结果对比情况Fig.4 Comparison between predicted and experimental results
3 受火后构件的撞击过程分析
3.1 构件的温度场
对不同受火时间后钢管混凝土构件的侧向撞击性能进行分析,除受火时间外,所有构件的撞击条件均相同。构件C0,C3,C6,C9,C12和C15的受火时间分别为0 min,30 min,60 min,90 min,120 min和150 min。构件C3,C9和C15典型的截面节点温度分布如图5所示。可以看出,对不同受火时间后的构件,外钢管的温度分布均匀,随着受火时间增加,外钢管温度升高。核心混凝土节点温度沿环向分布均匀,节点温度由混凝土外表面向核心区逐渐降低,出现明显的温度梯度,这与混凝土的热惰性和导热能力有关。构件C3,C9和C15的混凝土核心区域温度分别达到260 ℃,630 ℃和700 ℃左右。
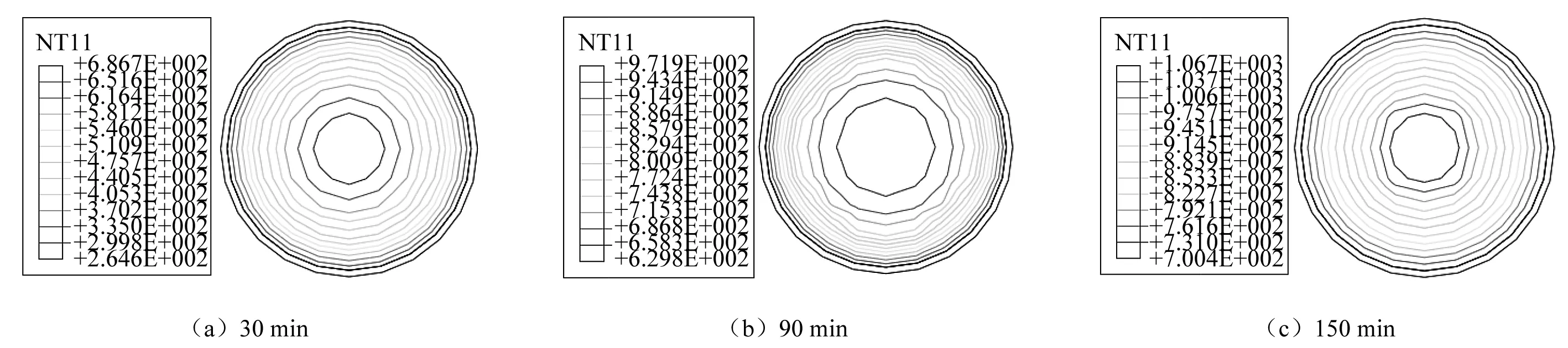
图5 构件截面的温度分布Fig.5 The distribution of sectional temperature on the members
3.2 构件的挠度与整体变形
不同构件的跨中挠度(u)时程曲线如图6所示。可以看出,受火时间对构件的跨中挠度影响明显,随着受火时间增加,挠度快速增大。构件C0,C3,C6,C9,C12和C15对应的极限挠度分别为24.8 mm,28.0 mm,34.1 mm,37.1 mm,39.5 mm和42.0 mm,与未受火相比,受火30 min,60 min,90 min,120 min和150 min后挠度增长的幅度分别为13%,38%,50%,59%和69%。对于不同受火时间的构件,前期挠度时程曲线基本重合,表明构件挠度发展速度基本一致。当挠度达到极限值后,又小幅降低,并保持在一定的值附近波动,其原因为落锤与构件分离后构件发生震荡,构件部分变形恢复,挠度有所减小。不同构件最终的整体挠度曲线如图7所示,l为距离构件跨中的距离,uf为构件最终残余挠度。可以看出,不同构件撞击后的最终挠度曲线均呈“弓”形,表明构件最终的破坏形态为弯曲变形,且随着受火时间增加,构件的整体变形逐渐增大。
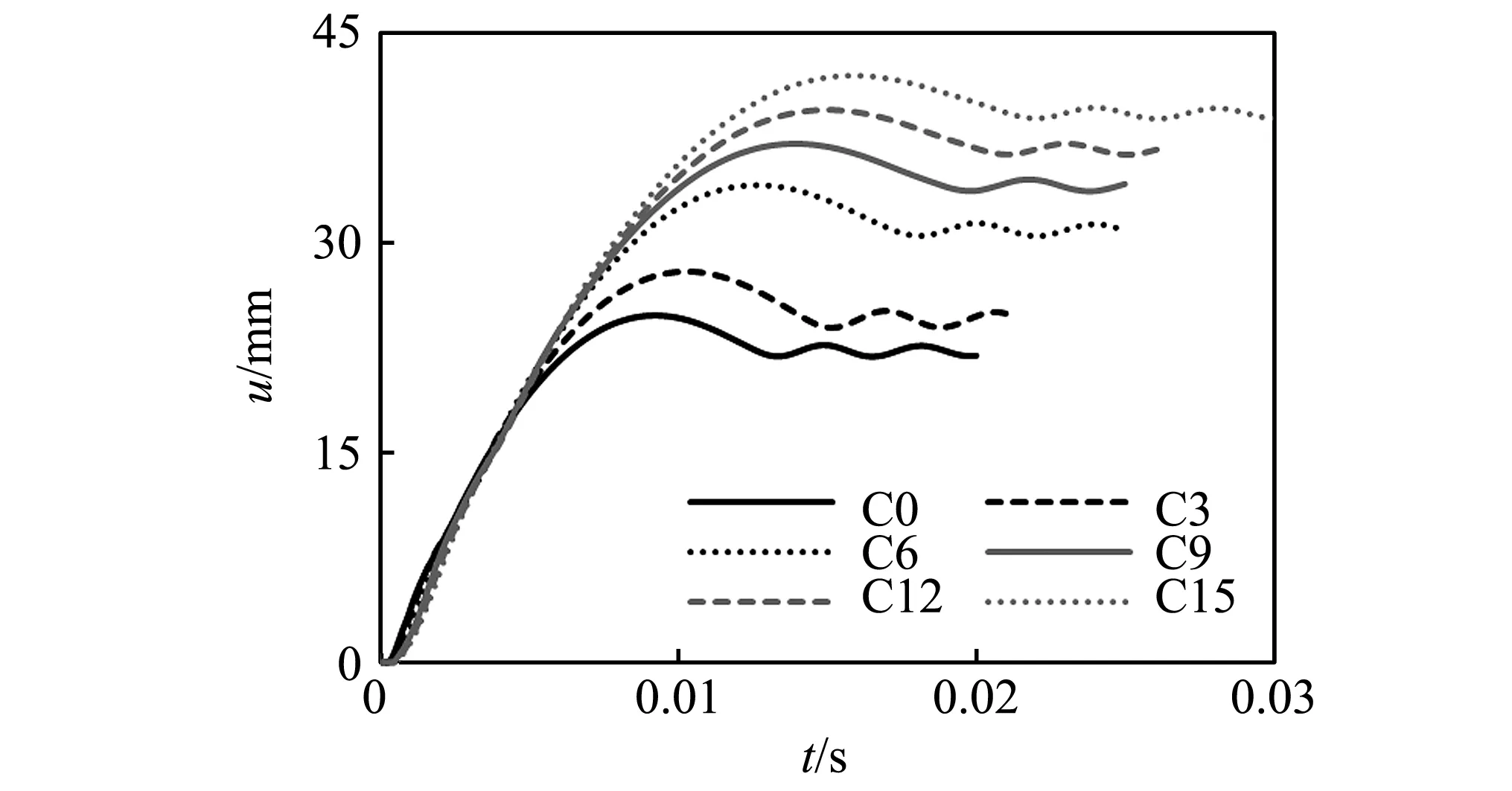
图6 不同构件的跨中挠度时程曲线Fig.6 Time history curves of mid-span deflection on different members
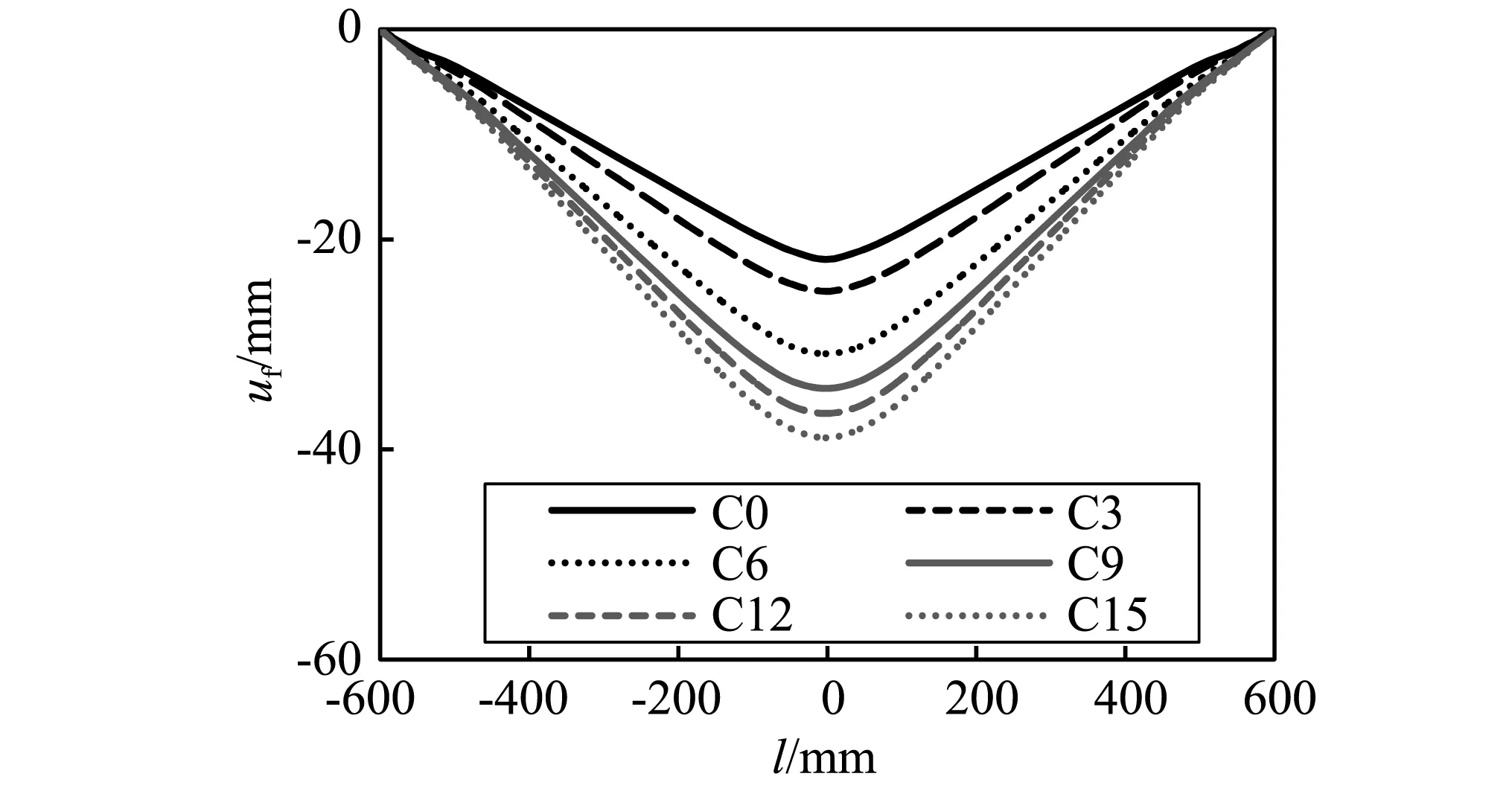
图7 构件的整体变形曲线Fig.7 Overall deformation curves of different members
3.3 撞击力时程曲线
不同构件的撞击力(F)时程曲线如图8所示。可以看出,不同受火时间后构件的撞击力时程曲线与未受火构件的撞击力时程曲线形态基本一致,其撞击力时程曲线有明显的三个阶段。以构件C9为例,其撞击过程可分为:峰值阶段(OC)、平台阶段(CD)和卸载阶段(DE),其中A点为撞击力峰值点,B点为撞击力最低点。此外,随着受火时间增加,构件的撞击力峰值大幅降低,撞击时程变长。构件C0,C3,C6,C9,C12和C15对应的撞击力峰值分别为289 kN,231 kN,165 kN,139 kN,123 kN和115 kN,其相应的撞击时程分别为0.012 6 s,0.014 4 s,0.017 3 s,0.018 9 s,0.020 s和0.021 2 s。其原因为受火时间越长,外钢管与核心混凝土强度降低的程度越严重,落锤与构件的接触刚度和构件的整体刚度均降低,导致撞击力峰值减小,接触时间变长。钢管混凝土构件撞击力时程曲线“平台阶段”的平台值与构件的抗弯能力有关,同时也可以反映构件的抗撞击性能。由图8可以看出,随着受火时间增加,构件的撞击力平台值逐渐降低。构件C0,C3,C6,C9,C12和C15的撞击力平台值分别为159 kN,149 kN,122 kN,110 kN,103 kN和93 kN,与未受火相比,受火30 min,60 min,90 min,120 min和150 min后降低的幅度分别为6%,23%,31%,35%和42%。这表明随着受火时间增加,构件的抗撞击能力和抗弯能力降低,因此也会产生更大的变形,这与3.2节跨中挠度随着受火时间增加的结论一致。

图8 不同构件的撞击力时程曲线Fig.8 The time history curves of impact force on different members
3.4 跨中截面的弯矩时程曲线
不同构件跨中截面的弯矩(MTd)时程曲线如图9所示。可以看出,跨中截面的弯矩时程曲线没有峰值阶段,但有明显的平台阶段。当截面弯矩达到某一极值左右时,弯矩较长的一段时间内保持相对稳定,该值为构件的截面动态极限弯矩[18],本文采用该值作为构件截面的动态极限弯矩(即构件在侧向撞击荷载作用下平台阶段的截面弯矩平均值)。此外,随着受火时间增加,构件的动态极限弯矩大幅降低,撞击时程变长。构件C0,C3,C6,C9,C12和C15的跨中截面动态极限弯矩分别为25.7 kN·m,23.8 kN·m,18.6 kN·m,16.9 kN·m,15.7 kN·m和14.7 kN·m,与构件C0相比,构件受火30 min,60 min,90 min,120 min和150 min后跨中截面动态极限弯矩降低的幅度分别为7%,28%,34%,39%和43%。表明构件的抗弯能力随着受火时间的增加逐渐降低。
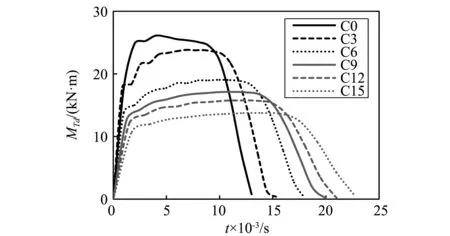
图9 构件跨中截面的弯矩时程曲线Fig.9 The time history curves of sectional moment atmid-span on different members
3.5 构件的弯矩和剪力分布
由于惯性力的存在,在撞击荷载作用下构件的弯矩分布会发生明显变化[19],以构件C9为例对火灾作用后构件的弯矩和剪力分布情况进行分析。图10为构件C9不同撞击时刻弯矩沿着构件长度方向的分布形态。可以看出,构件跨中和两端区域的弯矩在整个撞击过程中逐渐增加,零弯矩点由构件跨中渐向两端移动。在峰值阶段的初始期(约1 ms之前),由于惯性力和撞击力的影响,在构件L/4和3L/4区域附近产生明显的负弯矩,这与相应的静态荷载作用时弯矩分布不同。随着撞击时间增加,当撞击力经过峰值阶段的最低点(图8中的B点,该点对应时刻为2 ms)后,构件弯矩分布变化逐渐减小,呈“V”型分布,弯矩分布形态与静态荷载作用时基本一致。在2 ms后至15 ms撞击过程中,弯矩分布形态保持稳定,仅正、负最大弯矩在某一弯矩值附近稳定变化,这与从图9中的弯矩时程曲线得到的结论一致。这表明惯性力对构件弯矩分布的影响主要在“峰值阶段”,惯性力和撞击力会明显改变该阶段构件的弯矩分布形态。
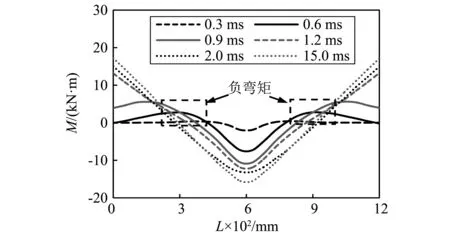
图10 构件C9的弯矩分布Fig.10 The distribution of the moment on C9 member
构件C9支座反力(FR)的时程曲线如图11所示。可以看出,支座反力时程曲线的形态与撞击力时程曲线基本类似,但曲线在撞击初期有明显的负支座反力。其原因为:在撞击初期,受惯性效应影响,构件有相对向上运动的趋势,从而产生了反向的支座反力。此外,支座反力在撞击开始至0.3 ms左右为零,但此时撞击力达到了约91 kN,撞击力和支座反力的变化存在一个时间间隔,这是因为应力波从跨中传向两端需要一定的时间[20]。
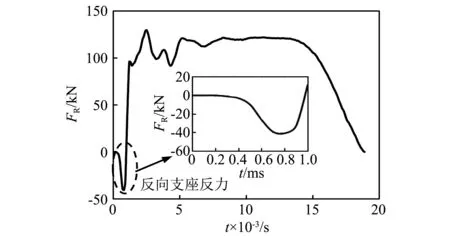
图11 构件C9的支座反力时程曲线Fig.11 The time history curve of reaction force on C9 member
构件C9不同撞击时刻剪力(V)沿着构件长度方向的分布情况,如图12所示。可以看出,在初始阶段约0.1 ms之前,剪力较大区域主要集中在跨中撞击区域两侧,同时在构件两端有明显的反向剪力区,且剪力分布不均匀,这与相应的静态荷载作用时明显不同。其原因为受到惯性力和撞击力的影响,这与图11中支座处出现反向支座反力的现象一致。此外,随着撞击时间增加,反向剪力逐渐消失,剪力向试件两端发展,且逐渐分布均匀,分布形态逐渐与静态荷载作用时一致。这表明惯性力仅对构件在“峰值阶段”的剪力分布有明显影响,对“平台阶段”的分布没有明显影响。
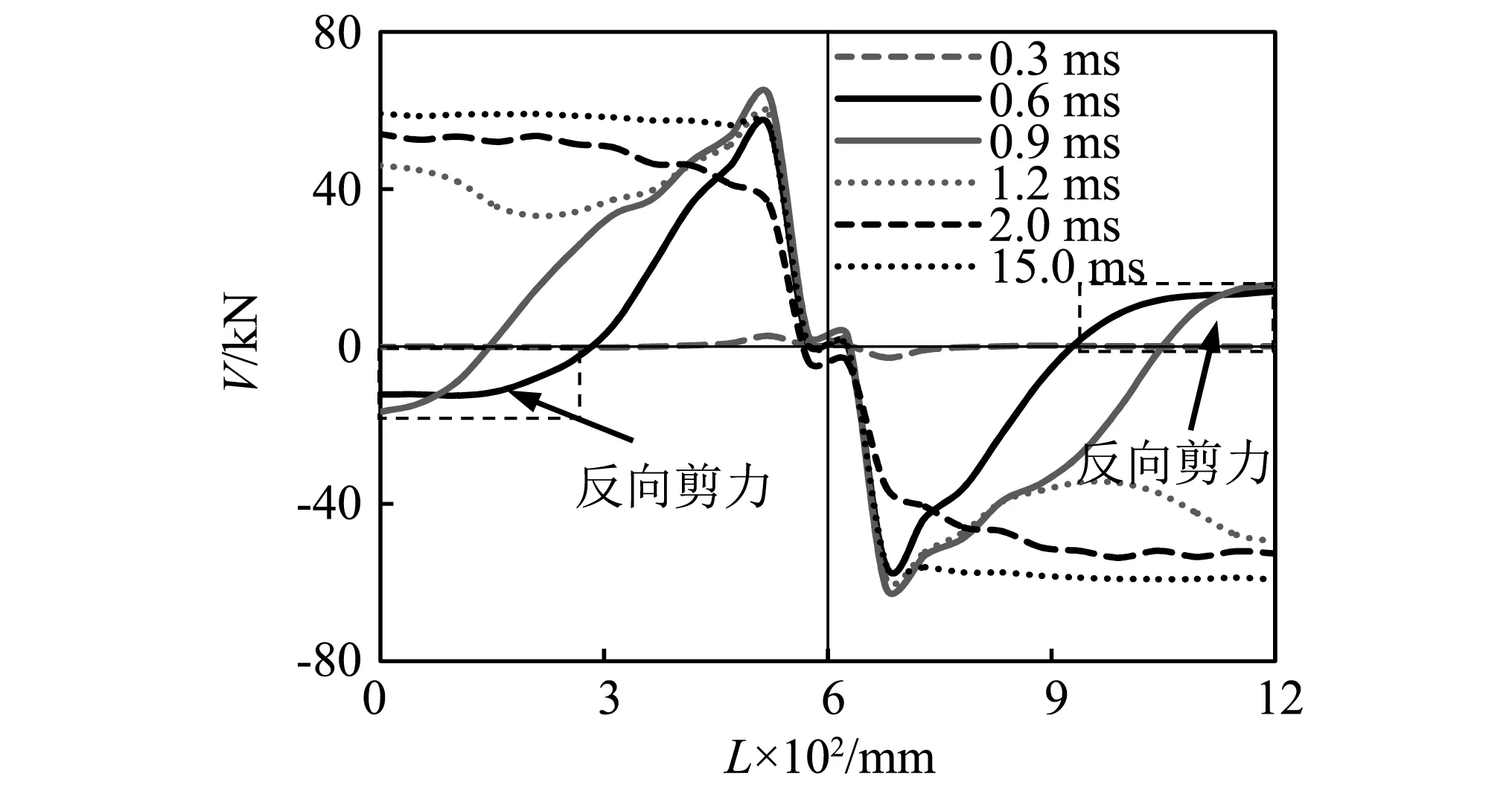
图12 构件C9的剪力分布Fig.12 The distribution of shear force on C9 member
4 构件抗撞击性能分析
4.1 撞击力-挠度曲线与吸能系数
不同构件的撞击力-挠度关系曲线如图13所示。可以看出,在峰值阶段,撞击力达到峰值后迅速降低,该阶段挠度发展较小。进入平台阶段后,撞击力保持在相对稳定的值,挠度迅速增大,构件的变形发展主要在该阶段。进入卸载阶段后,构件撞击力迅速减小至零,挠度有所减小。Eg构件的撞击力-挠度曲线围成的面积表示由构件整体变形所吸收的能量,Eg可由式(6)求得
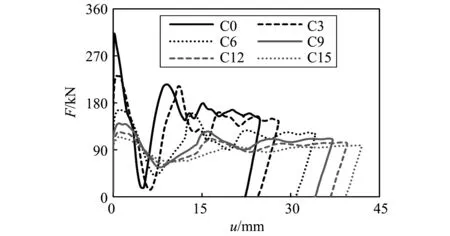
图13 构件的撞击力-挠度曲线Fig.13 Impact force versus deflection curves of different members

(6)
式中:uf为构件跨中的残余挠度;F(u)为撞击力随着构件跨中挠度变化的函数。
计算求得构件C0,C3,C6,C9,C12和C15对应的Eg分别为3 778 J,3 644 J,3 651 J,3 626 J,3 602 J和3 622 J,落锤的初始动能(E0)即为撞击的总能量,E0为4 320 J。构件的Eg/E0分别为0.87,0.84,0.85,0.85,0.83和0.84,可见,约85%初始动能由构件整体变形吸收,其余少部分能量通过落锤的剩余动能、构件的局部变形吸收,以及构件的震荡等形式耗散。这表明整体变形是受火后构件在侧向撞击荷载作用下的主要耗能机制。
吸能系数(μ)可以反映构件变形时的吸能能力[21]。μ的表达式为
(7)
式中:Ea为构件变形所吸收的能量;m为构件的质量;g为重力加速度值;ut为构件跨中截面的全部挠度(即构件跨中顶部表面的挠度),其表达式为
ut=uf+δ
(8)
式中,δ为构件跨中截面的局部变形。由于构件整体变形吸收了约85%的初始动能,局部变形较小,由局部变形耗散的能量较少,故计算时忽略掉局部变形所耗散掉的能量,构件的Ea值采用构件整体变形所吸收的能量Eg。
不同受火时间(to)后构件的吸能系数如图14所示。可以看出,随着受火时间增加,构件的μ快速降低,当受火时间超过60 min后,μ降低的幅度逐渐减小。与未受火的构件C0相比,构件在受火60 min后μ降低了33%,构件在受火150 min后μ降低了47%。这表明受火时间的增加会严重降低构件的抗撞击能力,其原因为:随着受火时间增加,钢管与混凝土的强度退化加重,构件产生了更大的变形。但当受火时间超过某一范围后,构件抗撞击性能随着受火时间增加而降低的幅度逐渐减小。

图14 构件的吸能系数(μ)Fig.14 The energy absorption capacity (μ) of the members
4.2 构件的动态极限弯矩与动态弯矩提高系数
受火时间对构件跨中截面动态极限弯矩分配的影响如图15所示。可以看出,随着受火时间增加,钢管与混凝土承担的动态极限弯矩均降低,但外钢管和混凝土各自承担的动态极限弯矩之比增大。这表明受火时间越长,钢管对构件抗弯承载力的贡献越大。如未受火的构件C0的外钢管承担了构件69%的动态极限弯矩,受火150 min后,构件C15外钢管承担了构件91%的动态极限弯矩。其原因为受火后当温度恢复至常温时,钢材的强度有所恢复,但混凝土的强度不能恢复,受火时间较长后,混凝土几乎丧失全部强度。
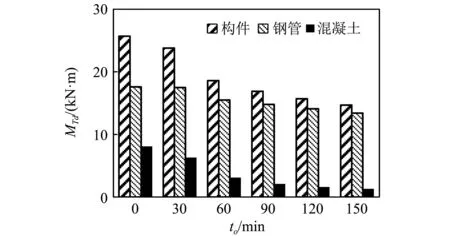
图15 构件跨中截面的动态极限弯矩分配Fig.15 The distribution of the dynamic ultimate moment on the members at mid-span
韩林海的研究给出圆钢管混凝土构件截面的静态极限弯矩(Mu)的计算公式,具体表达式如式(9)~式(13)
Mu=γm·Wscm·fscy
(9)
γm=1.1+0.48ln(ξ+0.1)
(10)
fscm=(1.14+1.02ξ)·fck
(11)
Wscm=π·D3/32
(12)
(13)
式中:γm为抗弯强度承载力计算系数;fscy为钢管混凝土的轴压强度承载力指标;Wscm为构件的截面抗弯模量;D为圆钢管混凝土的截面直径;ξ为钢管混凝土的约束效应系数;As为钢管的截面面积,Ac为核心混凝土的截面面积;fy为钢材的屈服强度值;fck为混凝土的标准抗压强度值。
采用动态弯矩提高系数可以反映构件截面动态极限弯矩与静态极限弯矩之比[22]。为反映温度对构件截面动态极限弯矩的影响,定义火灾后动态弯矩提高系数RT,以反映构件在火灾作用后的截面动态极限弯矩与常温下静态极限弯矩之比,具体表达式为
RT=MTd,u/Mu
(14)
式中,MTd,u为受火后构件的截面动态极限弯矩,该值可由数值计算得到。不同构件的火灾后动态弯矩提高系数RT如图16所示,可以看出,随着受火时间增加,RT快速减小,当受火时间超过90 min后,RT逐渐小于1.0,即构件的动态极限弯矩小于其静态极限弯矩,表明构件的抗弯承载力损失严重。在受火30~60 min,RT下降速度明显,其原因为构件抗弯承载力损失主要在该受火时间段。

图16 构件的火灾后动态弯矩提高系数RTFig.16 Post-fire dynamic increase factor of flexural capacity(RT) of the members
4.3 火灾作用后构件跨中最大挠度的计算公式
构件C9被撞击后外钢管的等效塑性应变和混凝土的应变如图17所示,其中混凝土云图上的矢量表示最大主应变的大小和方向。可以看出,外钢管在跨中撞击区域和两端区域产生明显的塑性变形,但跨中与端部之间区域没有塑性变形,表明构件在跨中与两端区域形成三处塑性铰。混凝土的主要变形区域也集中在构件跨中和两端。已有研究均表明两端固支的钢管混凝土构件在侧向撞击荷载作用下在两端和跨中共形成三处塑性铰。瞿海雁等的研究提出两端固支的钢管混凝土构件在侧向撞击荷载作用下的等效“塑性铰”模型,如图18所示。跨中截面的塑性铰绕两端转动的角度θ表达式为

图17 构件C9撞击后的塑性变形Fig.17 Plastic deformation of the member C9 after impact
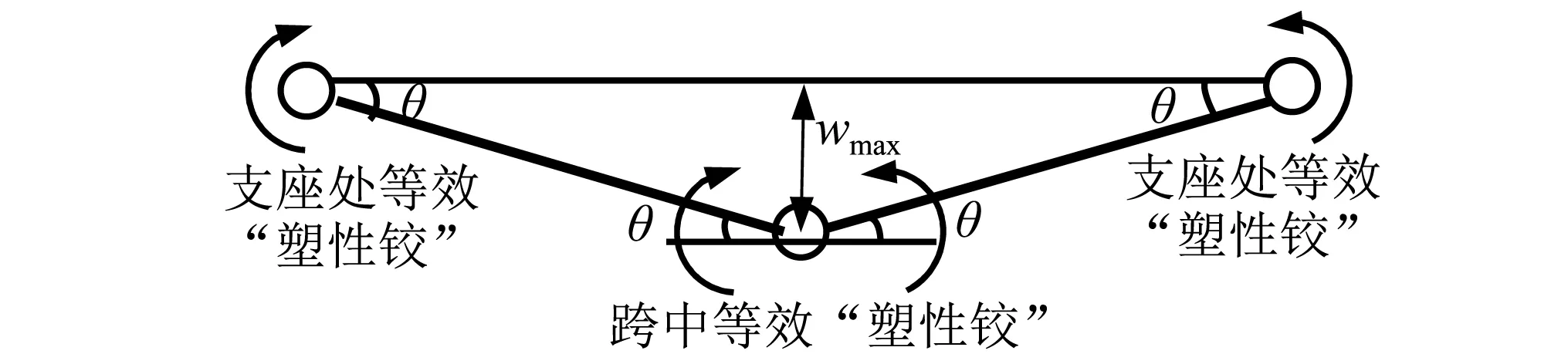
图18 三处“塑性铰”简化分析模型Fig.18 The simplified analysis model of three “plastic hinge”
(15)
式中:Ke为撞击的动能,Mp为跨中截面的动态极限弯矩。
本文采用该简化分析模型计算火灾作用后构件在撞击荷载作用下的跨中最大挠度(wmax)。跨中挠度(w)与θ的关系采用式(16)计算
(16)
式中:L为构件的长度。wmax计算的表达式可表示为
(17)
构件跨中最大挠度的模拟值与计算值对比情况如图19所示,umax/wmax的平均值为1.01,均方差为0.018,可见,计算值与模拟值吻合良好,说明该公式可以很好地计算火灾作用后构件在撞击荷载作用下跨中的最大挠度,也进一步反映了模拟的火灾作用后构件跨中截面动态极限弯矩的准确性。
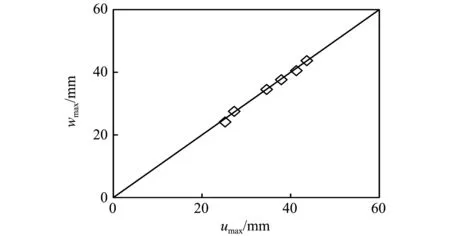
图19 公式计算最大挠度与模拟值对比Fig.19 Comparison between calculated and predicted maximum deflections
5 结 论
通过比较不同受火时间后钢管混凝土构件在撞击荷载作用下跨中挠度、撞击力和跨中截面弯矩的时程曲线,对构件弯矩和剪力分布形态、撞击力-挠度曲线、吸能系数、截面动态极限弯矩和火灾后动态弯矩提高系数进行分析,并给出火灾作用后构件跨中最大挠度计算公式,在本文研究范围内,得出以下结论。
(1) 受火时间对构件的跨中挠度和撞击时程影响明显,随着受火时间增加,火灾后构件的跨中挠度大幅度增加,撞击时程变长,构件的破坏形态为整体弯曲变形。
(2) 火灾作用后构件的撞击力时程曲线可分为峰值阶段、平台阶段和卸载阶段。随着受火时间增加,构件的撞击力平台值和截面动态极限弯矩逐渐下降,表明构件的抗撞击能力和抗弯能力降低。惯性力对构件弯矩和剪力分布的影响主要在“峰值阶段”,会明显改变弯矩和剪力的分布形态。
(3)构件主要通过整体变形吸收落锤的动能,随着受火时间增加,构件的吸能系数逐渐降低,但当受火时间超过某一范围后,构件的吸能系数下降的幅度逐渐减小。
(4)受火时间对构件截面动态极限弯矩的分配影响明显,随着受火时间增加,外钢管与混凝土各自承担的动态极限弯矩之比增大,表明钢管对构件抗弯承载力的相对贡献逐渐增大。构件的火灾后动态弯矩提高系数随着受火时间增加逐渐降低。
(5) 基于等效“塑性铰”简化分析模型,给出火灾作用后的构件在侧向撞击荷载作用下跨中最大挠度的计算公式,公式计算的最大挠度值与模拟的最大挠度吻合良好。

