环境激励下输电塔动力特性参数识别

赵 超， 赵家钰， 孙 清， 袁 俊， 王虎长， 贺育明， 谭 蓉

(1. 西安交通大学 人居环境与建筑工程学院，西安 710049；2. 中国电力工程顾问集团 西北电力设计院有限公司，西安 710075；3. 中国能源建设集团 陕西省电力设计院有限公司，西安 710054)

电力系统是国家的生命线工程，我国一直将电力系统的建设定为国家的发展要务，作为电力系统的载体，输电铁塔的安全性能显得尤为重要。在输电铁塔所承受的众多荷载中，风荷载是铁塔的主要负载，其设计取值受阻尼比的影响很大，在GB 50009—2012《建筑结构荷载规范》[1]中已明确指出阻尼比是确定风振系数中共振因子的关键参数，它的取值将对风振系数产生很大影响。但目前各国规范中对阻尼比的取值规定却各不相同，我国《建筑结构荷载规范》中规定钢结构的阻尼比应取0.01，美国ASCE74《输电线路设计导则》中指出铁塔阻尼比取值为0.04，澳大利亚荷载规范中规定铁塔阻尼比取值0.02。由于阻尼比是表征结构系统发生振动后能量耗散的特征参数，它与组成结构的材料特性，内部连接形式，以及结构的自振频率、振幅等参数有关。因此，由于阻尼机制的复杂性[2]，在工程实际应用中，确定阻尼比取值最有效的手段是进行实测。

本文以一基110 kV挂线输电塔为背景，采用环境随机激振法和牵引绳激振法对输电塔施加激振作用，通过沿塔身高度布置的加速度拾振器对铁塔的振动响应信号进行采集，采用修正平均周期图法对各测点的实测加速度响应信号进行去除噪声处理，在考察峰值频率相干度在95%的基础上，采用半功率带宽法对该输电塔的频率和阻尼比进行识别与分析。

1 测试方案

1.1 测试输电塔概况

本文测试的输电塔位于陕西省西安市浐灞东路，所属线路为1271-产等线。该塔为110 kV双回路角钢输电塔，塔身总高25 m，呼高15 m。输电塔的测试现场如图1所示，塔身上已安装导线和地线，该塔的正视图和侧视图如图2所示。现场测试时，场地视野开阔，人流量稀少，四周无明显障碍物遮挡。

图1 测试输电塔Fig.1 Field diagram of test transmission tower

图2 输电塔正视及侧视图Fig.2 Face view and side view of test transmission tower

1.2 激振方法

在结构振动测试试验中，常采用激振方法有两大类，分别为环境随机激振法和人工激振法[3]，本文采用环境随机激振和人工激振法中的牵引绳激振，对测试输电塔施加激振作用，研究不同类型的激振方法对结构动力参数测试与识别的影响。

牵引绳激振方法的现场加载装置如图3所示。在测试中，将一根钢丝绳索的上端连接到输电塔上，并将其下端分别锚固在平行和垂直导线方向的地锚上，通过底部安装的倒链葫芦张紧绳索，使输电塔产生初始位移，当绳索张力达到预设值后，通过解锁装置突然卸去荷载，结构将产生有阻尼的自由振动[4]。该激励方法激振能量集中，响应信号的信噪比高，但该激振方法对场地要求较高，需开挖场地埋设地锚等装置，现场组装设备耗时费力[5]。此外，若测试输电塔处于正常工作状态时，该激振法可能会影响到线路的正常运行。

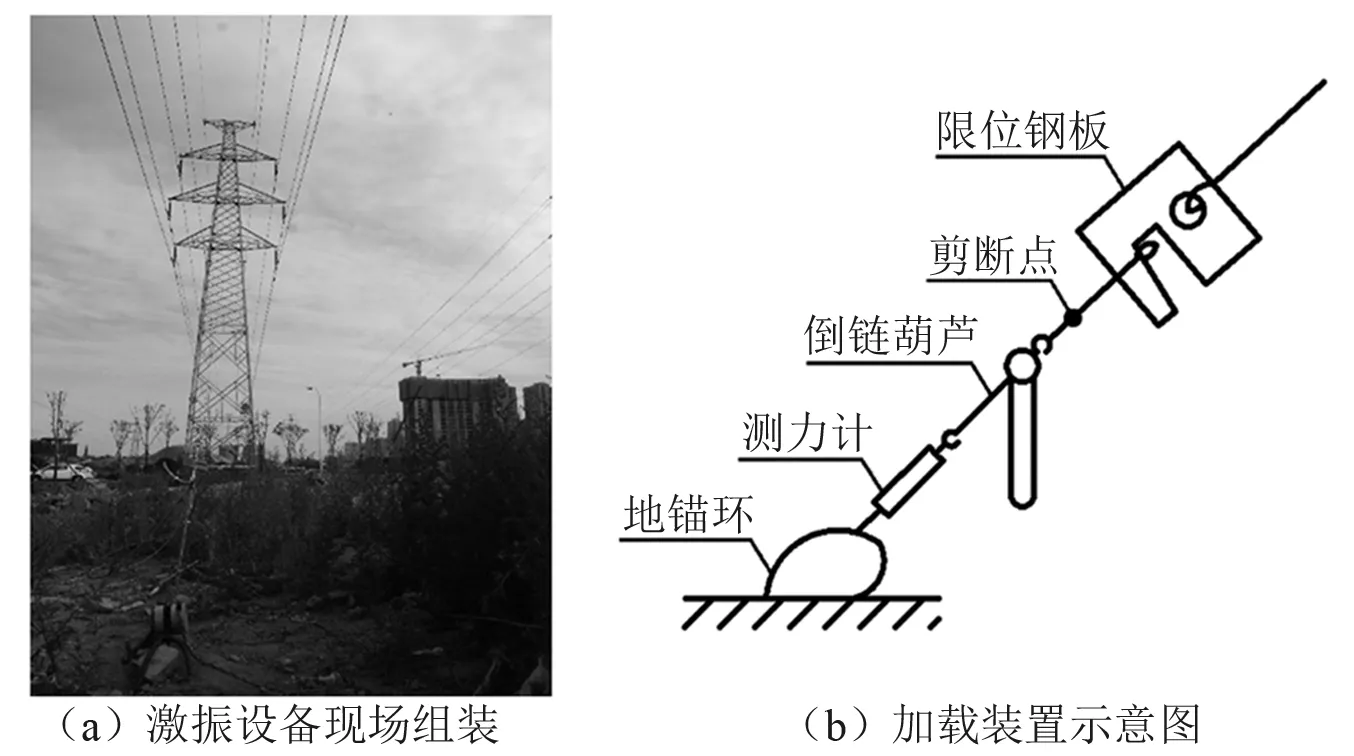
图3 牵引绳激振法Fig.3 Artificial excitation method

环境随机激振是将引起结构振动的自然地脉动和脉动风作为激振源，以此实现对输电塔的激振作用，该激振法无激振设备的要求，试验简便，所需的人力少，不受场地、测试结构类型的限制，广泛应用于野外现场实测试验中。但由于激振效果微弱，所测数据的信噪比偏低，易受噪声干扰的影响[6]，因此采用该方法时，通过监测场地的风速和减少可控噪声的产生，可以改善现场实测条件，提高测试数据精度。

1.3 振动测试系统

为采集测试输电塔的振动响应信号，在测试现场组装了一套完整的振动测试系统，如图4所示。沿塔身高度方向共布设8个测点，每个测点上均安装有加速度传感器。

图4 振动测试系统布置Fig.4 Layout of vibration testing system

加速度传感器为中国地震局工程力学研究所研制的941B型超低频拾振器，如图5所示。该型号传感器最大量程为20 m/s2，灵敏度为0.3 V·s2/m，为单轴加速度传感器，可采集结构的加速度响应信号。加速度传感器通过信号屏蔽线与INV3062C型数据采集仪相连接，如图6所示，该数据采集仪可完整的采集带宽在0～108 kHz的有效信号，并通过有线传输的方式传送到电脑设备终端记录。

图5 超低频941B型拾振器Fig.5 Type of 941B vibration pickup

图6 INV3062C数据采集仪Fig.6 Type of INV3062C data acquisition instrument

现场采集前，首先对拾振器进行归一化调试。然后根据测点布置图，将拾振器安装在塔身上，并通过信号屏蔽线与采集仪相连，调试采集设备，设置采样频率为50 Hz，确认各通道的一致性后，分别采用环境随机激振和牵引绳激振的方式对输电塔施加激振作用，分别采集并记录平行输电塔横担方向和垂直输电塔横担方向的加速度响应信号，用于自振频率和阻尼比等动力特性参数的分析。

2 阻尼比识别方法

2.1 数据前处理方法

本试验在数据采集的过程中，不可避免地受到周围环境噪声的影响，导致所采集到的信号里包含一定量的噪声信号。为消除噪声信号对结构真实响应的干扰，需首先对数据进行降噪处理。

周期图法[7]是一种功率谱函数估计的经典方法，常被用于消除数据信号中噪声干扰的影响，其方法原理为

(1)

(2)

图7 修正的平均周期图法Fig.7 Modified periodogram algorithm method

这样就减小了分段数增大对图形分辨率的影响，并使方差得到进一步减小。同时，由于噪声信号的存在具有随机性，即噪声的干扰不可能在每一段数据中都相同的存在，所以运用此方法处理就可以将噪声信号加以压制，同时提取出有用的响应信号。

由于汉宁窗函数可以使信号在频域阶段下的旁瓣互相抵消，消去高频干扰和漏能，改善由于矩形窗产生的谱失真问题，有利于提高阻尼比等振动参数的识别精度[10]，故本文在利用修正平均周期图法对数据进行前处理的同时，采用汉宁窗对数据进行加窗处理，长度为M的汉宁窗公式为

(3)

得到的采用加汉宁窗的修正平均周期图法为

(4)

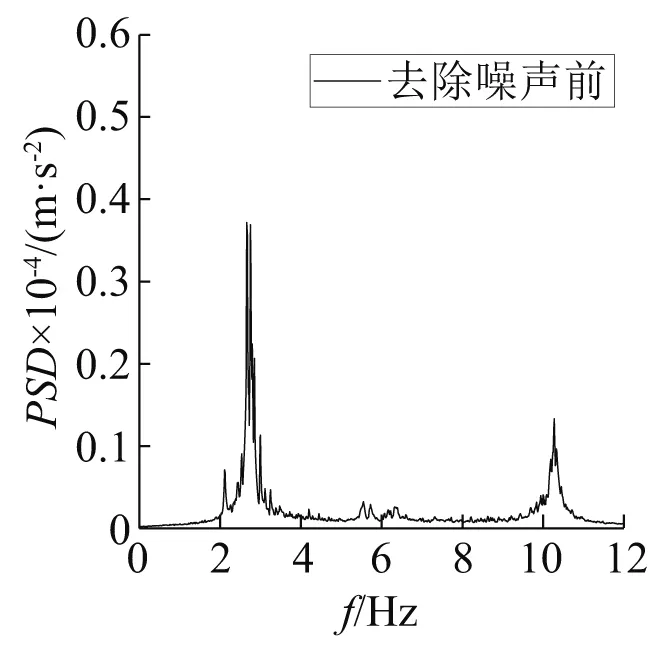
图8 去除噪声前响应信号幅-频曲线Fig.8 Amplitude-frequency curve of response signal before noise removal

图9 去除噪声后响应信号幅-频曲线Fig.9 Amplitude-frequency curve of response signal after noise removal

2.2 阻尼比识别方法

(5)

求解时，由于ξ≪1，故忽略ξ2以上小量，得到阻尼比

(6)

3 试验结果及分析

3.1 自振频率识别结果

采用两种不同的激振方法对输电塔施加激振作用后，各测点采集的加速度响应信号如图10和图11所示。

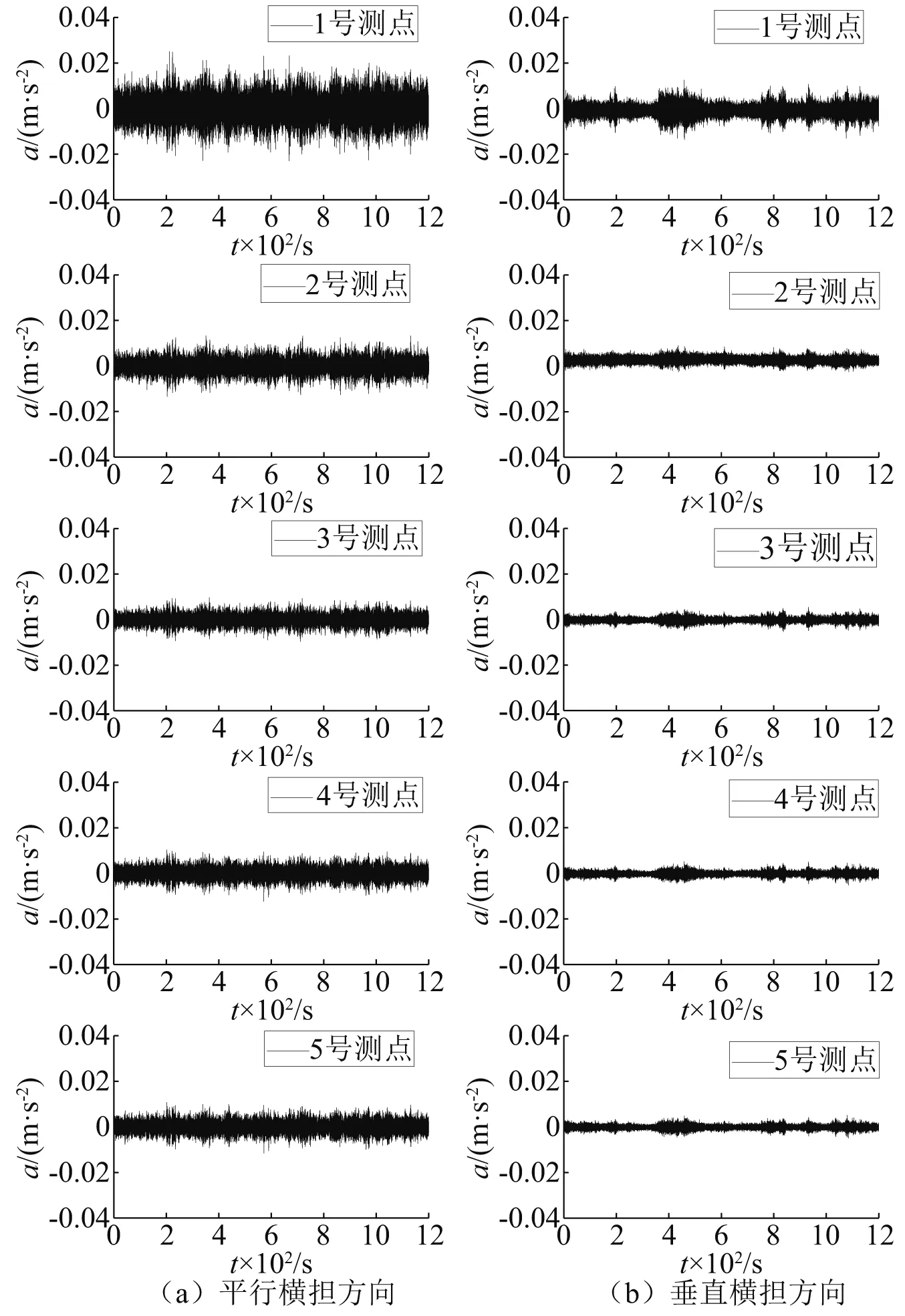
图10 环境激振法下各测点加速度响应Fig.10 Acceleration response under ambient excitation

图11 牵引绳激振法下各测点加速度响应Fig.11 Acceleration response under artificial excitation

对于采集到的加速度时程响应信号，首先利用前述加设汉宁窗的修正平均周期图法，对数据进行去除噪声处理，通过频谱分析，分别做出施加环境随机激振和牵引绳激振后各测点的幅-频特性曲线，如图12和图13所示。从图中可以看出，经去除噪声后，幅-频曲线中主峰峰值明显突出，且各测点的峰值频率表现出了高度的一致性，将识别的峰值频率列入表1和表2中。

图12 施加环境随机激振后响应信号的幅-频曲线Fig.12 Amplitude-frequency curve of ambient excitation

图13 施加牵引绳激振后响应信号的幅-频曲线Fig.13 Amplitude-frequency curve of artificial excitation

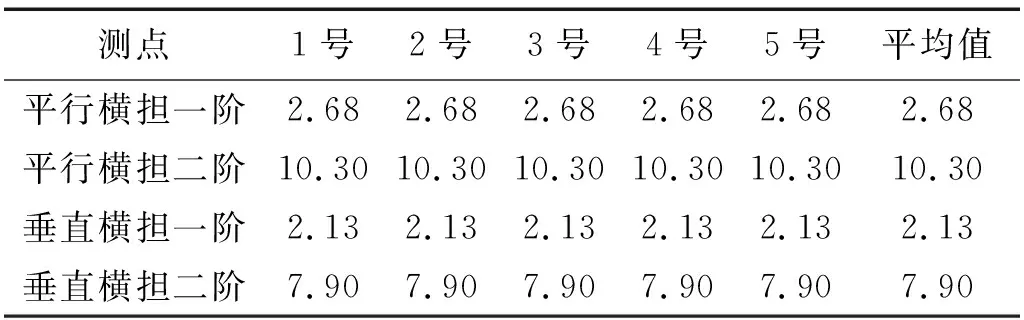
表1 环境激振法结构自振频率识别结果Tab.1 Recognition results of structures natural frequencies under ambient excitation Hz

表2 牵引绳激振法结构自振频率识别结果Tab.2 Recognition results of structures natural frequencies under artificial excitation Hz

由表1可知，采用环境激振法，识别出平行横担方向一阶频率为2.68 Hz，二阶频率为10.30 Hz；垂直横担方向一阶频率为2.13 Hz，二阶频率为7.90 Hz；根据表2可知，采用牵引绳激振法，识别出平行横担方向一阶频率为2.65 Hz，二阶频率为10.30 Hz；垂直横担方向一阶频率为2.15 Hz，二阶频率为8.35 Hz。

采用两种不同的激振方法时，平行横担方向和垂直横担方向的一阶自振频率接近，但在两个方向的功率谱中均可清楚识别。考虑到输电塔在两个方向质量和刚度分布相似的特点，识别结果与实际状态吻合。

3.2 数据有效性分析

进行振动信号采集时，存在噪声信号干扰。为了保证实测数据的可靠性，检验峰值频率的真实性，提高半功率带宽法识别阻尼比的精度，对测点峰值频率的相干性进行考查，如图14和图15所示，分别为施加环境随机激振和牵引绳激振下测点峰值频率相干度。

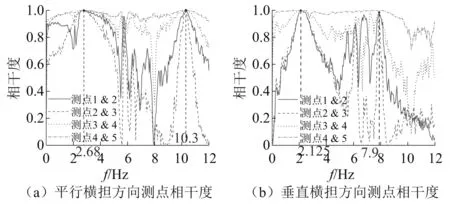
图14 环境随机激振下峰值频率相干度Fig.14 Coherence of peak frequency under ambient excitation

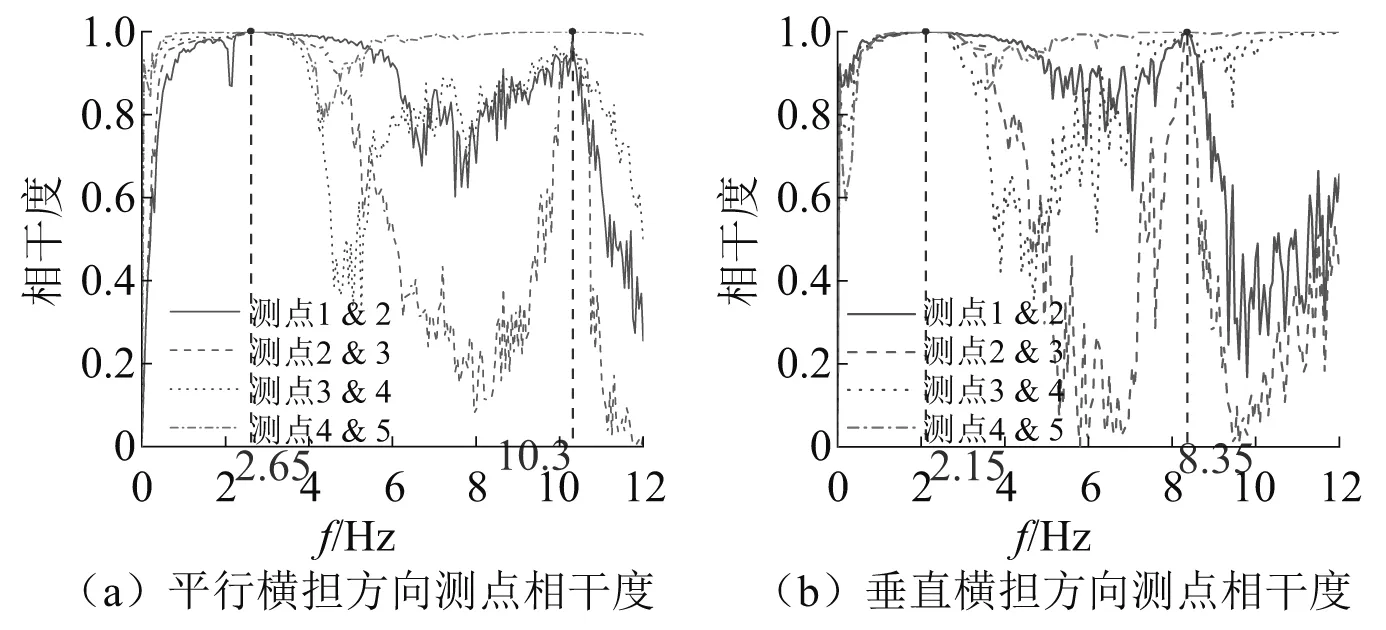
图15 牵引绳激振下峰值频率相干度Fig.15 Coherence of peak frequency under artificial excitation

环境激励下，平行横担方向一阶频率相干度为99.97%，二阶频率相干度为98.73%；垂直横担方向一阶频率相干度为99.95%，二阶频率相干度为97.00%。牵引绳激励下，平行横担方向一阶频率相干度为99.98%，二阶频率相干度为96.73%；垂直横担方向一阶频率相干度为99.98%，二阶频率相干度为97.86%。

从图14和图15可知，各激振方法下的测点在峰值频率处的相干性均达到了95%以上，说明数据中的噪声干扰已基本去除，所识别的模态频率为结构系统的真实频率。

3.3 阻尼比识别结果

在去除噪声并判别数据真实有效后，采用半功率带宽法，对所测输电塔进行阻尼比参数识别，如表3和表4所示，表3和表4分别为施加环境随机激振和牵引绳激振下阻尼比的识别结果。

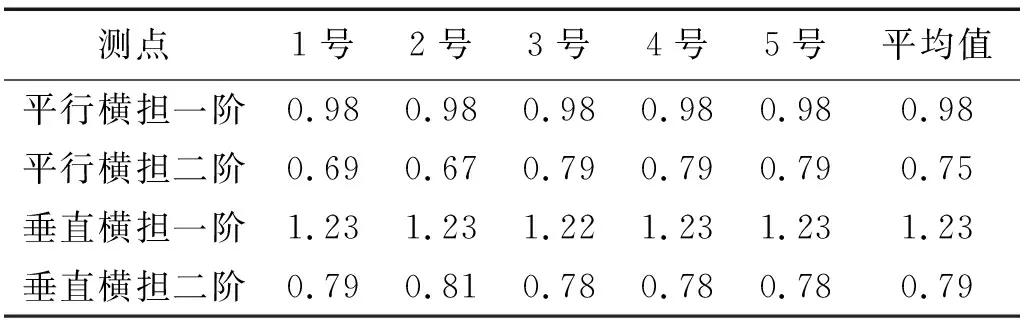
表3 环境随机激振法阻尼比识别结果Tab.3 Damping ratio recognition of ambient excitation %

表4 牵引绳激振法阻尼比识别结果Tab.4 Damping ratio recognition of artificial excitation %

采用环境随机激振时，所识别的平行横担方向的一阶阻尼比为0.98%，二阶阻尼比为0.75%，垂直横担方向的一阶阻尼比为1.23%，二阶阻尼比为0.79%；采用牵引绳激振时，所识别的平行横担方向的一阶阻尼比为0.99%，二阶阻尼比为0.78%，垂直横担方向的一阶阻尼比为1.25%，二阶阻尼比为0.82%。

对比两种激振方法下所识别的阻尼比数值可以看出：当采用不同的激振方法施加激振作用时，所识别的输电塔阻尼比数值接近，最大误差在5%以内，说明本文提出的修正平均周期图法进行数据降噪处理后，采用半功率带宽法，可有效识别激励作用下结构的阻尼比。

4 结 论

本文以位于陕西省西安市浐灞东路110 kV输电塔为测试对象，采用了环境随机激振和牵引绳激振分别对其施加激振效应，研究了输电塔的动力参数识别问题，对比分析了不同激振方法下的阻尼比识别情况，得出以下结论：

(1) 采用修正平均周期图法，对实测数据进行降噪处理，处理后的响应信号主峰峰值突出，旁瓣峰值降低，不均匀“毛刺”现象削弱，功率谱峰值提高36.8%。

(2) 采用半功率带宽法进行识别时，峰值频率的误差将影响阻尼比识别，因此在去除噪声的基础上，考察峰值频率的相干性大于95%，保证识别结果准确。

(3) 采用环境随机激振和牵引绳激振对输电塔进行激振，结果表明：两种方法识别的一阶阻尼在0.98%～1.25%内，误差小于5%，为采用环境激振法进行输电塔的动力测试提供参考依据。