多级齿轮传动转子系统的模态缩减与振动特性分析
韩健明, 杨 翼, 马清雅, 王滋华, 戴义平
(西安交通大学 能源与动力工程学院,西安 710049)
齿轮传动转子系统在能源、电力、机械、化工、航空、船舶和车辆等行业的动力设备中起着重要作用,其动力学和振动特性直接影响到整机设备的振动噪声和稳定运行,相关研究具有重要的理论价值和工程意义,受到国内外学者的广泛重视。
对于单级齿轮传动的两轴系统,Rao等[1]提出了齿轮传动转子系统的通用有限元模型,对含减速齿轮的透平电机转子系统进行了弯扭耦合自由振动分析,探究了齿轮啮合刚度对固有频率和模态振型的影响。Saxena等[2]利用ANSYS Workbench平台对齿轮转子系统进行了模态分析,并研究了轴承刚度的变化对系统固有频率的影响。蒋庆磊等[3]建立了齿轮传动转子系统的通用模型,对大功率离心泵轴系进行了振动及响应分析,并研究了齿轮副耦合作用对振动特性的影响。结果在轴系设计和机组运行稳定性方面具有实际意义。车永强[4]采用有限元法计算了未耦合和耦合的齿轮-转子系统的临界转速、振型、弯振不平衡响应和扭振不平衡响应。王逸龙等[5]以某航空发动机转子为研究对象,基于集中参数法建立了带阻尼环的齿轮传动转子系统的弯扭耦合动力学模型,分析了其在工作频率范围内的动力学响应。常乐浩等[6]提出了适用于平行轴外啮合圆柱齿轮-轴-轴承-箱体系统动力学建模的有限单元法,并以一对单级斜齿轮传动为例,通过与已有实验数据的对比验证了该方法的有效性。
对于多级多轴齿轮传动转子系统,庞辉等[7]分析了某三平行齿轮减速系统的固有频率、振型和受迫振动响应特性,结果表明,多级齿轮传动转子系统的振动通常为各轴间的弯扭耦合振动,且各轴上的不平衡会引起整个系统的振动。张义民等[8]基于模态叠加法,对膨胀机系统进行了固有特性分析和瞬态方式的不平衡响应分析,得到齿轮啮合前、后系统加载处的不平衡响应变化曲线。王奇斌[9]计算了齿轮传动转子系统在定转速、变转速下的不平衡响应以及静态传递误差引起的系统动力学响应。朱丽莎等[10]以压缩机转子系统为例,基于有限元法,建立了通用的弯-扭-轴-摆斜齿轮耦合动力学模型,并分析了系统的固有特性和不平衡响应。
综上所述,国内外学者在单级或多级齿轮传动转子系统的建模和振动特性方面开展了大量的研究工作,文献[11]研究了单级齿轮传动转子系统的模态缩减。然而,多级齿轮传动转子系统结构复杂、自由度多、求解时间长,而且由于齿轮耦合作用,多个转子振动相互耦合,系统动力学行为复杂,有必要关注多级齿轮传动转子系统的简化及其振动特性分析。因此,本文提出了一种适用于多级齿轮传动转子系统的模态缩减法,以某工程项目的透平驱动水泵系统为研究对象,通过有限元法建立了系统动力学模型,并利用模态缩减法减少了系统自由度。在此基础上研究了系统的固有特性、不平衡量与静态传递误差引起的稳态响应、启动状态下的瞬态响应以及稳定运转下突加不平衡时的瞬态响应。
1 齿轮传动转子系统有限元建模
1.1 齿轮啮合模型
本文建立的12自由度斜齿轮三维动力学模型如图1和图2所示,齿轮副被简化为两个由弹簧-阻尼单元连接的刚性圆盘。r1与r2为齿轮基圆半径;α12为齿轮的方位角,表示齿轮的相对位置;β12为螺旋角,主动轮左旋时大于0,右旋时小于0;ψ12为主动轮y轴正方向与啮合平面的夹角。位移向量可表示为

图1 斜齿轮副三维动力学模型Fig.1 Three-dimensional dynamic model of a helical gear pair
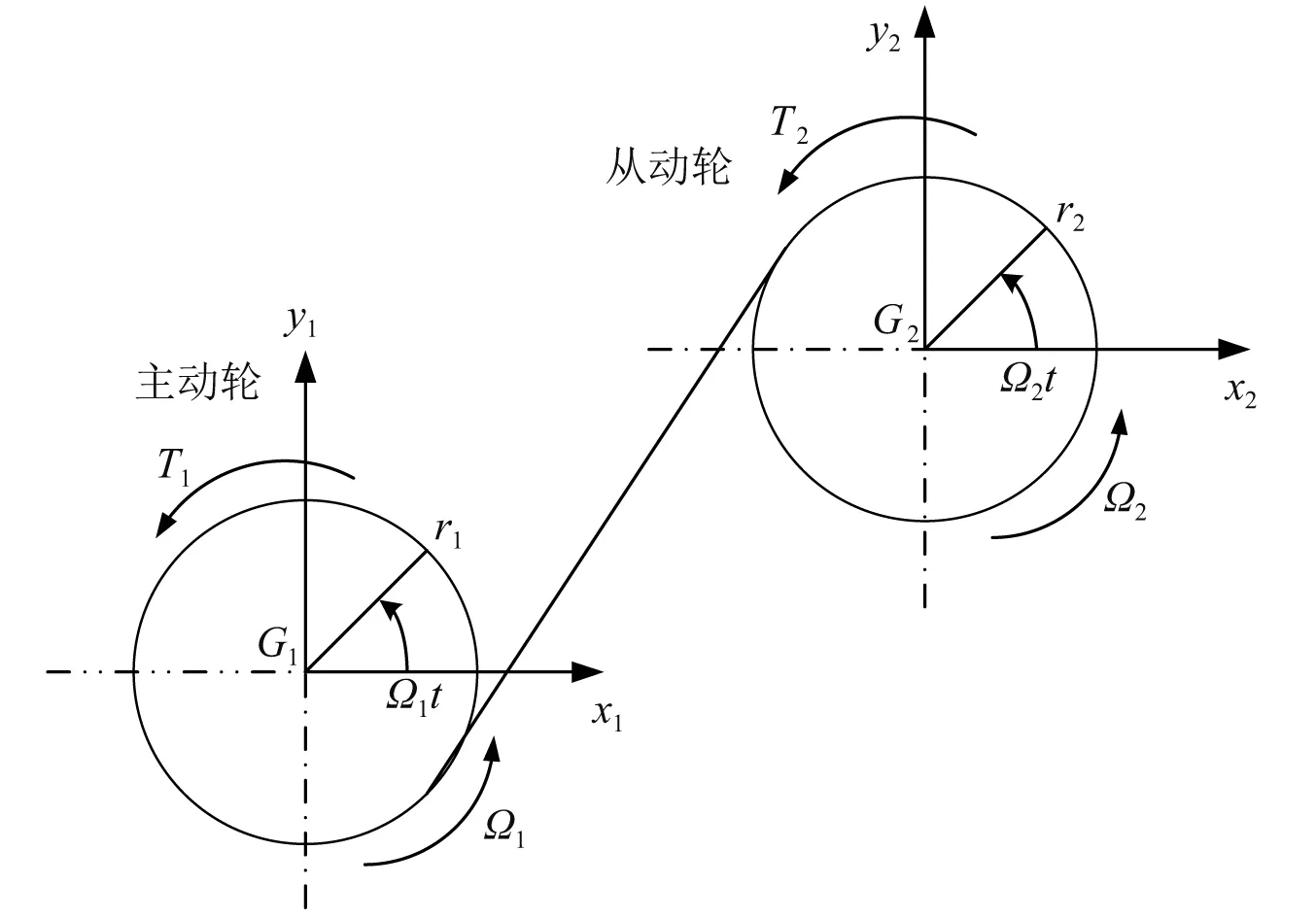
图2 z方向投影图Fig.2 Projection drawing in z-direction
qg=[x1,y1,z1,θx1,θy1,θz1,x2,y2,z2,θx2,θy2,θz2]T
(1)
式中:x,y和z为横向自由度;θ为扭转自由度。假设齿轮副受到不平衡激励,根据牛顿第二定律,齿轮副的运动微分方程为

(2)
其中,
Mg,i=diag(mi,mi,mi,Iix,Iiy,Iiz)
(3)
(4)
qg,i=[xi,yi,zi,θxi,θyi,θzi]T
(5)
(6)
(7)
(8)
Tg,i=[0,0,0,0,0,Ti]T
(9)
(10)
(11)
式中:U为不平衡量;h12为齿轮副在啮合线方向的相对位置,用位移向量表示为
h12(t)=[(-x1+x2)sinψ12+(y1-y2)cosψ12+
r1θz1+r2θz2]cosβ12+(z1-z2+r1θx1sinψ12+
r2θx2sinψ12-r1θy1cosψ12-
r2θy2cosψ12)sinβ12-e12(t)
(12)
式中,e12(t)为静态传递误差激励,其定义为
e12(t)=e12sin(N1Ω1t)
(13)
式中:e12为幅值;N1,Ω1分别为主动轮1的齿数和转速。
1.2 转子系统模型
转子系统的典型有限元模型由三部分组成:轴段、轴承和刚性圆盘。本文根据Stringer[12]所提出的方法建立轴段、轴承和刚性圆盘的有限元模型,获得相应的质量矩阵M、陀螺矩阵G和刚度矩阵K。阻尼假设为比例阻尼。由此即可得到单个转子系统的运动方程

(14)
式中:M,C和K为n阶矩阵,分别表示质量、阻尼和刚度矩阵;F为外力矢量。阻尼矩阵包含两部分,广义阻尼矩阵D和反对称的陀螺矩阵G。
2 模态缩减
2.1 坐标变换矩阵
Garvey等[13-14]提出了一种坐标变换的方法,可将单个转子系统的运动方程式(14)转换为一阶状态空间方程
(15)
其中,
(16)
式中,I为单位矩阵。这种坐标转换方法的关键是得到两个2n阶的矩阵TL和TR, 使得它们满足式(17)
(17)
式中,Md,Cd和Kd分别为对角化后的质量、阻尼及刚度矩阵。物理坐标与主坐标之间的转换关系可表示为
u=TRv
(18)

(19)
通过以下4个步骤得到转换矩阵TL和TR:
步骤1求解式(15)的特征值λi=αi±jβi并得到左右两个特征向量矩阵ΦL和ΦR,ΦR为标准化后的特征向量矩阵。将特征值排列成两个对角矩阵Λ1=diag[α1+jβ1,α2+jβ2,…,αn+jβn]和Λ2=diag[α1-jβ1,α2-jβ2,…,αn-jβn]。同时重新排列两个特征向量矩阵ΦL和ΦR,使其中的特征向量与Λ1和Λ2中的特征值相对应。
步骤2计算得到矩阵Md,Cd和Kd。其中Md=I,Cd=diag[ci],Kd=diag[ki]。ci和ki由式(20)得出

(20)
步骤3求解式(19)的特征值,并得到左特征向量矩阵EL和标准化后的右特征向量矩阵ER满足式(21)
(21)
式中,Λ=diag[Λ1,Λ2]。
步骤4将式(21)进行变形
(22)
由此可得到
(23)
2.2 整体系统方程
假设齿轮转子系统有m个轴,每个转子视作一个子系统。将每个子系统的运动方程写成式(15)的形式后,组装得到整体系统的运动方程
(24)
式(24)简写为
(25)
式(25)所给出的整体系统的运动方程并没有考虑齿轮啮合效应。耦合了第i个和第j个转子的齿轮啮合刚度矩阵可写为
(26)
Stringer等[15]认为单级齿轮传动的两轴系统的状态空间矩阵表示为
(27)
对于一个n轴系统,式(27)应修改为
(28)
其中,
(29)
式中,Astif,k为耦合了第i个和第j个转子的第k个齿轮啮合刚度矩阵。对于一个m轴系统,至少应有m-1个齿轮副来保证系统的稳定运行。因此,k=1,2,…,N(N≥m-1)。这样,整体的齿轮啮合刚度矩阵就可表示为
(30)
根据整体齿轮啮合刚度矩阵的形成方法同理可得整体齿轮啮合阻尼矩阵Bdamp。由此,式(25)改写为
(31)
整体的转换矩阵TL,s和TR,s由各子系统的转换矩阵TL,i和TR,i(i=1,2,…,n)组装得到,组装方法与式(24)类似。整体主坐标与物理坐标之间的关系表示为
us=TR,svs
(32)
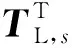
(33)

3 结果与讨论
3.1 有限元模型的验证
为了不失一般性,通过现有文献中一个实例来验证上述有限元模型。以Rao等提出的透平电机转子系统为验证对象,该系统由透平转子、电机转子和直齿轮副组成。该转子系统的简图如图3所示。对于直齿轮来说,螺旋角为0°,其它参数与Rao等文中所给一致。齿轮啮合刚度为1×108N/m时工作转速下的固有频率,如表1所示。同时,也给出了Rao等的计算结果作为对比。很明显,两组结果在各阶固有频率上都有着很好的一致性,证明了本文的有限元模型有着较高的精度。

图3 透平电机转子系统模型Fig.3 Sketch diagram of the turbo-generator rotors system

表1 透平电机转子系统的固有频率Tab.1 Natural frequencies of the turbo-generator rotors system (rad/s)
3.2 固有频率分析
以某工程项目的透平驱动水泵系统为研究对象,系统结构如图4所示。透平转子的工作转速为5 600 r/min。一级齿轮传动比为33/122,齿轮啮合刚度为2.85×108N/m,模数为4 mm,压力角为20°。二级齿轮传动比为34/87,齿轮啮合刚度为3.42×108N/m,模数为8 mm,压力角为20°。轴承B7,B8,B9和B10是滚动轴承,其它为滑动轴承。图5为该系统所对应的等效系统图。整个系统划分为36个节点,共216个自由度。
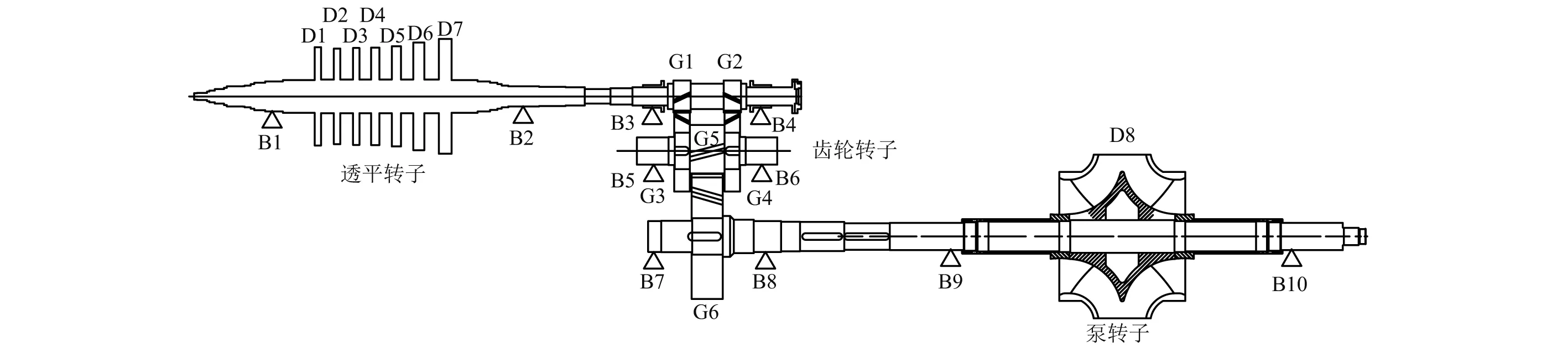
图4 透平驱动水泵系统Fig.4 Sketch diagram of the turbine driven pump system

图5 等效系统图Fig.5 The diagram of equivalent system
图6和图7分别为未耦合与耦合系统的Campell图。从中可以看出,齿轮耦合改变了系统的模态。相比于未耦合系统,耦合系统出现了两个新的固有频率,如图7中箭头所示。未耦合系统的1阶、2阶、3阶和4阶模态与耦合系统的3阶、4阶、5阶和6阶模态相差不大。相比于未耦合系统,耦合系统的部分固有频率如7阶、8阶减小了。这是由于齿轮将各转子耦合在一起后相当于增加了转子长度,因此部分受耦合效应影响的固有频率有所降低。此外,受陀螺效应影响,固有频率随转速的变化而变化,但变化并不明显。

图6 未耦合系统的Campell图Fig.6 The Campell diagram of uncoupled system

图7 耦合系统的Campell图Fig.7 The Campell diagram of coupled system
表2为完整自由度模型(216个自由度)与100个、80个、60个、40个自由度模型在工作转速下的前14阶固有频率,同时也给出了相应的偏差(以完整模型结果为标准)。当保留60个自由度时最大偏差仅为1.32%,保留40个自由度时最大偏差也仅为2.25%,意味着仅需要较少的自由度即可很好地预测系统的固有频率。
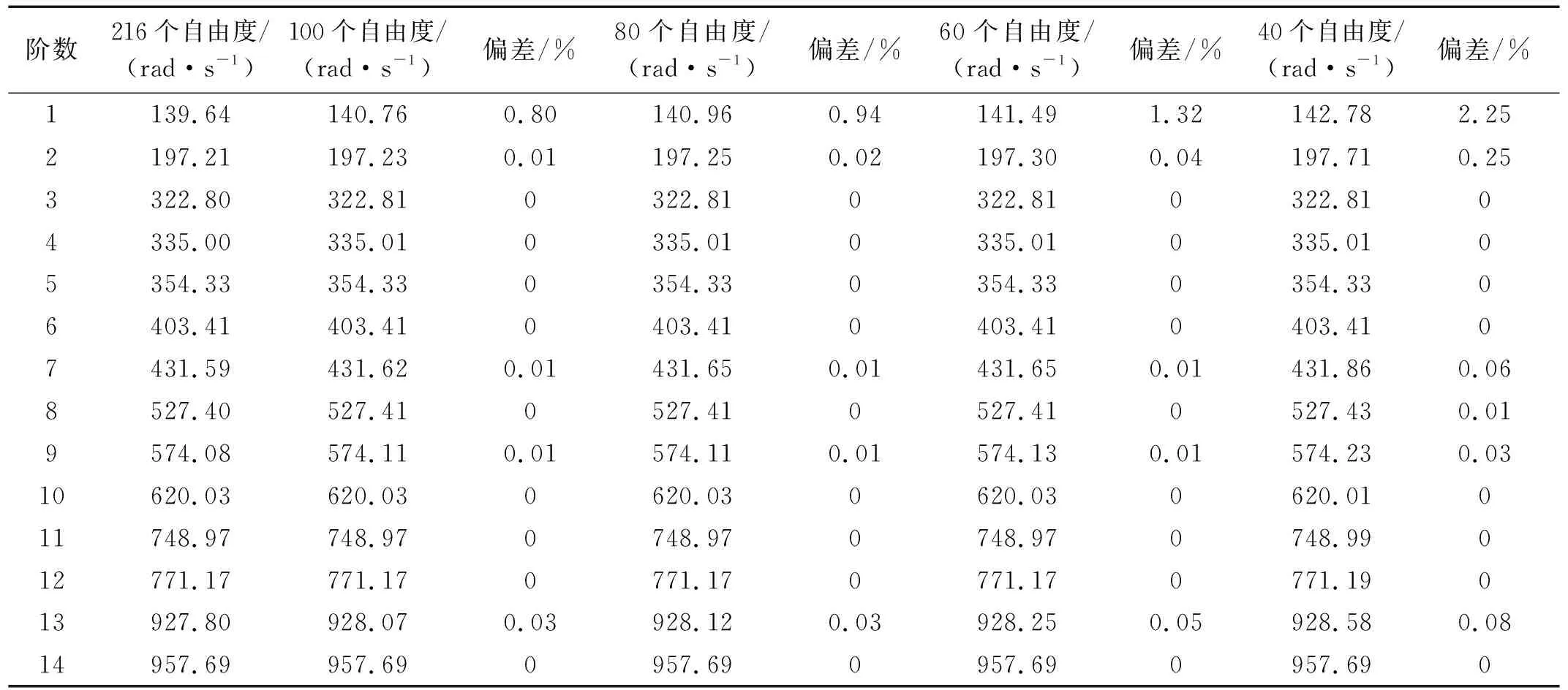
表2 工作转速下固有频率的偏差Tab.2 Error percents of natural frequencies at operational speed
3.3 稳态响应分析
本节对不平衡量及静态传递误差引起的稳态响应进行分析。根据美国石油协会标准[17]确定系统不平衡量的施加位置和大小,在D5处施加不平衡量2 004 g·mm。图8是系统D7处的不平衡响应曲线。可以看出,在给定转速范围0~7 000 r/min内,仅在临界转速3 087 r/min附近有一个波峰。相比于完整模型,缩减后的模型仍然具有很高的精度。

图8 系统D7处不平衡响应Fig.8 Response due to mass unbalance of D7
齿轮啮合的静态传递误差是指实际啮合位置与理论位置在啮合线上的偏差。齿轮的加工安装误差和变形都会引起传递误差。静态传递误差幅值为0.5×10-6m,频率为齿轮啮合频率。系统D7处的响应曲线如图9所示。在给定的转速范围0~7 000 r/min内存在多个峰值,且0~1 000 r/min内存在最大峰值。这说明静态传递误差激励在低转速范围内(0~1 000 r/min)就可以激发系统的高阶模态,引起系统剧烈振动,因此在对齿轮动力学的设计和分析中有必要重视静态传递误差激励的作用和影响。在转速大于2 000 r/min之后,40个自由度模型计算出的结果偏差较大,这是因为静态传递误差激励可以在低转速下激发系统的高阶模态,当缩减了较多的自由度后,一些高阶模态被丢弃,导致精度下降。所以在计算静态传递误差引起的响应时,应保留一定数量的自由度。

图9 系统D7处静态传递误差激励引起的响应Fig.9 Response due to static transmission error of D7
3.4 瞬态响应分析
首先对系统启动时的瞬态响应进行分析。在圆盘D7处给定一初始不平衡量U=156 g·mm。为简化计算,将透平的启动规律进行简化,使其以111.28 rad/s2的加速度启动至工作转速。采用4~5阶自适应变步长的龙格库塔法求解系统的运动方程,并获得了启动响应曲线。系统启动过程中X和Y方向的振幅如图10和图11所示。从图中可以看出,在系统启动至1.5 s,4 s以及5 s附近时,振幅增大,振动剧烈,相应的转速分别接近于转速为1 883 r/min,4 120 r/min和5 036 r/min的临界转速。完整自由度模型与100个、80个、60个、40个自由度模型的计算时间分别为69 856.77 s,3 016.49 s,1 601.74 s,542.46 s和119.37 s。
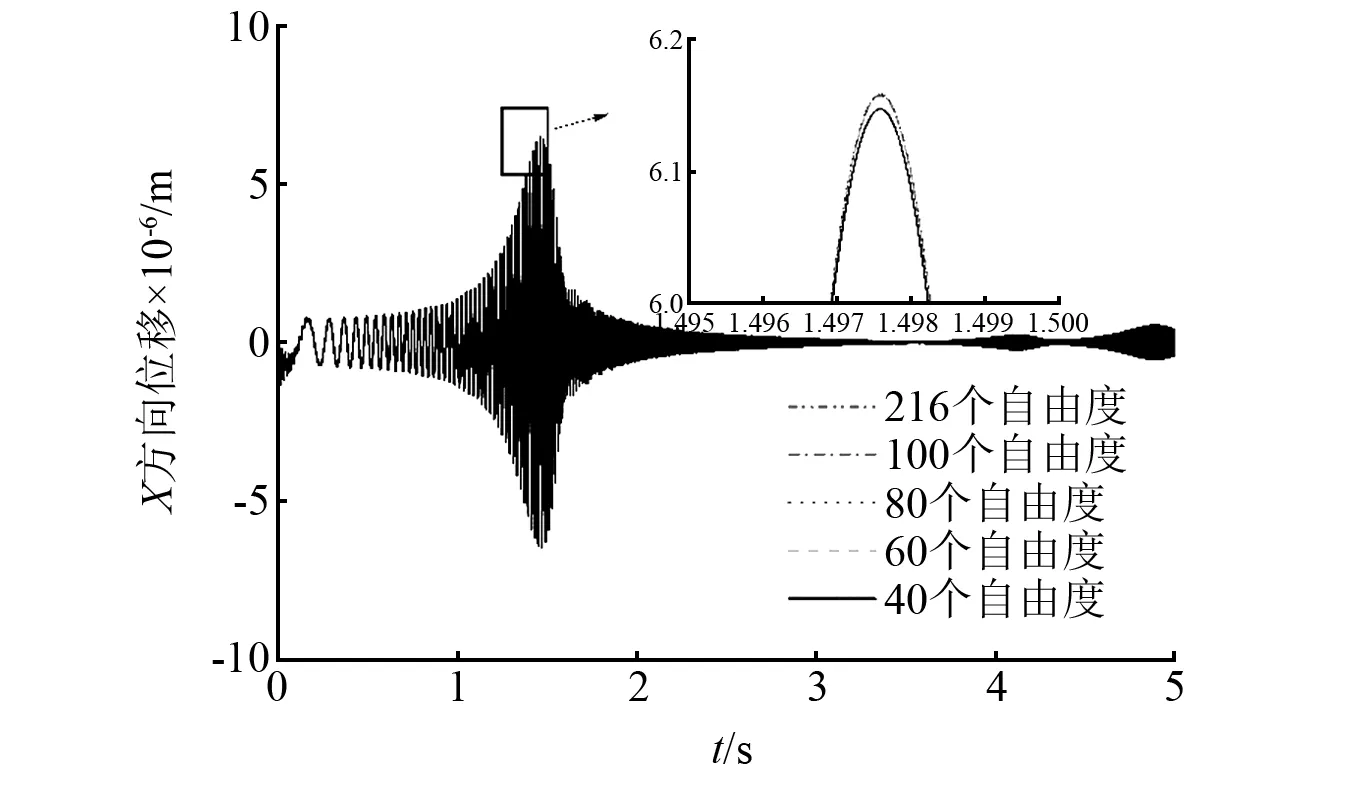
图10 启动状态下D7处X方向振幅Fig.10 X-direction amplitude at D7 in the startup state

图11 启动状态下D7处Y方向振幅Fig.11 Y-direction amplitude at D7 in the startup state
转子系统在运转过程中可能由于转子零件松脱或叶片断裂等原因造成不平衡量突然增大,为研究这种情况下的瞬态响应特性,当系统运转至某一时刻时,将系统不平衡量增大至780 g·mm。突加不平衡后转子系统在工作转速下的瞬态响应特性如图12和图13所示。从图中可以看出,在转子系统运转至1 s时突加不平衡,经过一段时间后瞬态响应消失,进入稳态阶段。计算具有216个、100个、80个、60个、40个自由度的模型所需要的时间分别为20 753.05 s,789.80 s,412.42 s,132.36 s和33.17 s。

图12 工作转速下突加不平衡D7处X方向振幅Fig.12 X-direction amplitude at D7 due to unbalance mutation at the operating speed

图13 工作转速下突加不平衡D7处Y方向振幅Fig.13 Y-direction amplitude at D7 due to unbalance mutation at the operating speed
相比于完整自由度模型,缩减自由度模型节省计算时间超过90%。表3为局部放大图中某一时刻不同自由度模型的振幅之间的偏差。以完整自由度模型为基准,缩减自由度模型结果的最大偏差仅为0.36%,说明仅需要很少的自由度参与计算,即可很好地预测系统的瞬态响应特性。

表3 瞬态响应振幅之间的偏差Tab.3 Error percents between transient response amplitude
4 结 论
本文采用有限元法,建立了多级多轴齿轮传动转子系统动力学模型,利用模态缩减法减少了系统自由度,并对缩减模型的准确性进行了验证,在此基础上研究了系统的振动响应特性,得到了如下结论:
(1) 齿轮耦合作用使系统产生了新的固有频率。此外,由于齿轮将各转子耦合在一起后相当于增加了转子长度,部分固有频率有所降低。
(2) 对于不平衡响应,相比于完整模型,缩减后的模型仍然具有很高的精度。静态传递误差激励在低速范围内(0~1 000 r/min)即可激发系统的高阶模态。因此,为保证计算精度,在计算静态传递误差激励引起的响应时应保留一定数量的自由度。
(3) 在启动过程中,由于自身不平衡量的作用,系统穿越临界转速时会发生不同程度的振动。在系统启动至1.5 s,4 s以及5 s附近的转速分别对应于转速为1 883 r/min,4 120 r/min和5 036 r/min的临界转速。当不平衡量发生突变时,系统发生剧烈振动,经过一段时间后瞬态阶段消失,进入稳态阶段。
(4) 利用模态缩减法剔除高阶模态后,大大缩减了计算时间。相比于完整自由度模型,缩减后的模型精度高,偏差小。因此,本文提出的模态缩减法在节省计算时间的同时也保证了计算准确性。

