既有桥梁对相邻车-桥系统气动力的影响分析

严乃杰， 吴 韬， 臧 瑜， 李永乐， 郑博文， 戴建国

(1. 中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081； 2. 西南交通大学 土木工程学院，成都 610031；3. 重庆市轨道交通(集团)有限公司，重庆 401120； 4. 上海市政设计工程研究总院(集团)有限公司，上海 200092)

随着城市交通的快速发展，城市桥位资源越来越宝贵，为了满足交通需求，常常需要在既有桥梁附近新建桥梁，如2007年通车的塔科马大桥平行桥，距原塔科马大桥仅61 m；2011年通车的新海河大桥，距原海河大桥仅35 m。当既有桥梁位于新建桥梁来流前方时，既有桥梁会干扰新建桥梁周围的流场，对作用在新建桥梁及桥上列车的气动荷载产生影响。已有研究表明：列车在桥梁、高路堤等结构物上运行时，在横向风荷载作用下，列车更容易发生列车倾覆等事故[1]。因此，桥上列车的气动特性也成为近年来的研究热点。对于大跨度轨道交通桥梁，主梁离地较高，桥面风荷载较大，导致桥上列车对风荷载的作用更敏感，车-桥系统受横向风的影响更明显，且作用在列车、桥梁上的气动力与车辆的位置密切相关，既有桥梁对新建桥梁车-桥系统气动力的干扰也更为复杂。

目前，国内外学者针对相邻桥梁的气动干扰现象开展了诸多研究。针对新建的塔科马平行桥，Irwin等[2]进行了节段模型和全桥气弹模型风洞试验，研究了两座桥梁间的气动干扰效应，包括施工状态、成桥状态的风荷载和气动稳定性。陈政清等[3-4]以平胜大桥、红岛航道斜拉桥为背景，研究了平行双箱梁桥面的颤振、涡振、静力气动特性，并分析了箱梁距离与气动干扰间的关系，结果表明相邻桥梁之间存在不可忽略的气动干扰。朱乐东等[5-6]以新建的海河大桥为背景，研究了既有桥梁对邻近新建桥梁颤振、涡振性能和气动力系数的影响。刘小兵等[7]引入干扰因子概念，研究了三种典型桥梁断面相互间的气动干扰效应，结果表明钝体断面的干扰效应更明显。秦浩等[8-9]通过全桥气弹模型试验、数值模拟，研究了大跨度双幅钢箱梁桥涡振特性，以及中央格栅抑制涡振的效果。JTG/T 3360-01—2018《公路桥梁抗风设计规范》指出：分离双幅桥梁净间距小于5倍单幅主梁宽度时，单幅桥梁的横向力系数的确定宜考虑双幅桥梁的气动力干扰效应。上述研究结果表明，相邻桥梁之间的气动干扰效应显著，在桥梁的设计中有必要考虑既有桥梁的影响。

已有研究均是针对相邻桥梁加劲梁间的气动干扰，如加劲梁颤振、涡振性能和静风特性等，关于既有桥梁对相邻车-桥系统的气动力干扰研究还未见报道。本文以某新建的悬索桥为工程背景，通过节段模型风洞试验，测试了考虑、不考虑既有桥梁干扰两种工况下车-桥系统的气动力系数，研究了既有桥梁对邻近车-桥系统气动力系数的影响。结合试验结果，模拟了车-桥系统抖振力时程，通过极值概率分布计算了车-桥系统抖振力的极值，分析了既有桥梁对邻近车-桥系统抖振力的干扰效应。

1 工程概况

本文以某新建的双塔三跨连续钢箱梁悬索桥为工程背景，该桥为城市轨道交通桥梁，设计时速80 km/h，跨径布置为50 m+210 m +600 m +210 m +50 m，梁宽22.0 m、高4.5 m，桥面布置人行道护栏、防抛网、疏散平台等附属设施，钢箱梁横断面如图1所示。在新建桥梁下游有一座既有桥梁，为双塔三跨连续钢箱梁公路悬索桥，跨径布置为211 m +600 m +211 m，梁宽35.5 m、高3.0 m，桥面布置了人行道护栏、中央分隔带，钢箱梁横断面如图2所示。两座桥梁轴线水平距离70 m，竖向高度差3.45 m。新建桥梁桥面设施数量多，桥面风环境相对复杂，且为轨道交通桥梁，车-桥系统对风荷载更加敏感。因此，本文主要研究既有桥梁对相邻新建桥梁车-桥系统气动力的影响。

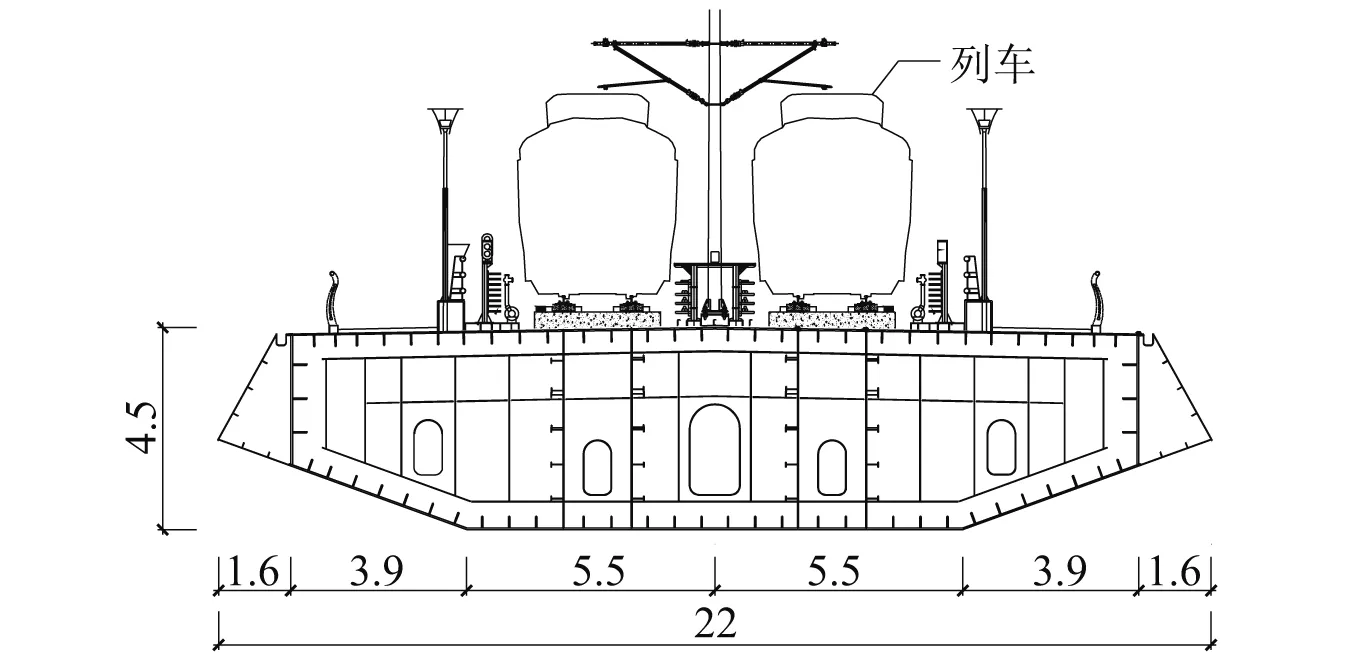
图1 新建桥梁钢箱梁横断面(m)Fig.1 Cross-section of steel box girder of new-built bridge (m)

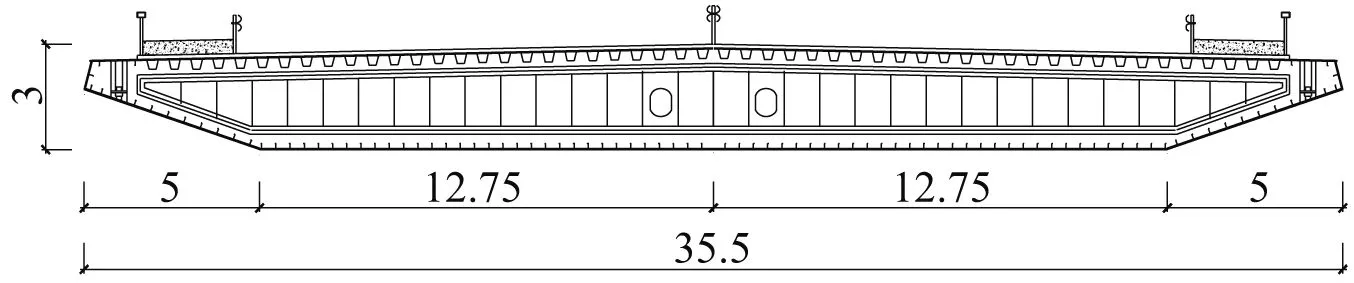
图2 既有桥梁钢箱梁横断面(m)Fig.2 Cross-section of steel box girder of existing bridge (m)

2 车-桥系统气动力模型

2.1 静风力

作用在单位长度桥梁上的静风力可以表示为

(1)

(2)

(3)

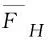
列车的截面形式为矩形，绕轴心的扭转力矩对列车响应的贡献较小，可以忽略不计[10]。当风速垂直于列车运动方向时，作用在单位长度列车上的静风力可表示为

(4)

(5)

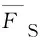
2.2 抖振力

体轴坐标系下，作用在单位长度桥梁上的抖振力可以表示为

(6)

(7)

(8)

式中：FH为桥梁抖振阻力；FV为桥梁抖振升力；MT为桥梁抖振升力矩；χ为导纳函数；u(t)为顺风向脉动风；w(t)为竖向脉动风。

研究中通常仅考虑顺风向脉动风对列车抖振力的贡献[11]。然而，已有研究表明横向风和竖向脉动风对列车抖振力的影响不容忽视[12]。为了更真实地模拟作用在移动列车上的抖振力，本研究同时考虑了顺风向、横风向和竖向脉动风。体轴坐标系下，作用在单位长度列车的抖振力可以表示为

(9)

(10)

式中：FS为列车抖振横向力；FL为列车抖振升力；v(t)为横风向脉动风；χiu，χiv，χiw为与不同风向脉动风有关的导纳函数；Ciu，Civ，Ciw为与抖振力有关的气动力系数，i=S,L。根据Yan等的推导结果，上述抖振力系数可表示为

(11)

(12)

(13)

3 车-桥系统气动特性风洞试验

试验在西南交通大学XNJD-1风洞第二试验段进行，试验段宽2.4 m、高2.0 m，风速范围为1.0～45.0 m/s。列车和桥梁模型缩尺比取1/40，模型长2.095 m，其中列车模型宽75 mm，高87.5 mm，风洞中车-桥系统节段模型如图3(a)所示。通过交叉滑槽系统实现桥梁、列车气动力分离，测试了考虑、不考虑既有桥梁影响两种状态下新建桥梁车-桥系统气动力系数。考虑既有桥梁影响下的车-桥系统节段模型，如图3(b)所示。

低风速下雷诺数较小，高风速下车-桥模型会发生振动而影响试验结果。因此，试验风速取15 m/s。试验中使用了一种自主研发的车-桥系统三分力测试装置——交叉滑槽系统，该装置能够实现车-桥系统的同轴转动，并能分别测试出车-桥系统中列车、桥梁的三分力，从而方便地进行不同攻角情况下的气动力的试验[13]。试验中分别测试了-3°～+3°风攻角下，考虑、不考虑既有桥梁影响时新建桥梁上无车/单车/双车组合工况下车-桥系统的气动力系数，试验工况如表1所示，试验结果如表2和表3所示。其中，单桥不考虑既有桥梁的影响；双桥考虑了既有桥梁的影响，且既有桥梁位于新建桥梁的来流前方，如图3(b)所示。

图3 车-桥系统节段模型Fig.3 Segmental model of vehicle-bridge system

表1 风洞试验工况Tab.1 Cases of wind tunnel test

由表2可知，受既有桥梁影响，当风攻角为-3°，0°时，不同位置列车的横向力系数均增大，升力系数基本均减小；其中，0°风攻角下单车过桥时背风侧列车横向力系数增幅最大，为39.3%；-3°风攻角下双车过桥时背风侧列车升力系数减幅最大，为-68.2%。当风攻角为+3°时，不同位置列车的横向力系数基本均减小，升力系数基本均增大；其中，双车过桥时背风侧列车横向力系数减幅最大，为-143.1%；单车过桥时背风侧列车升力系数增幅最大，为52%。需要注意的是：双车过桥时，受迎风侧列车的遮挡，背风侧列车的气动力系数均显著小于迎风侧的。

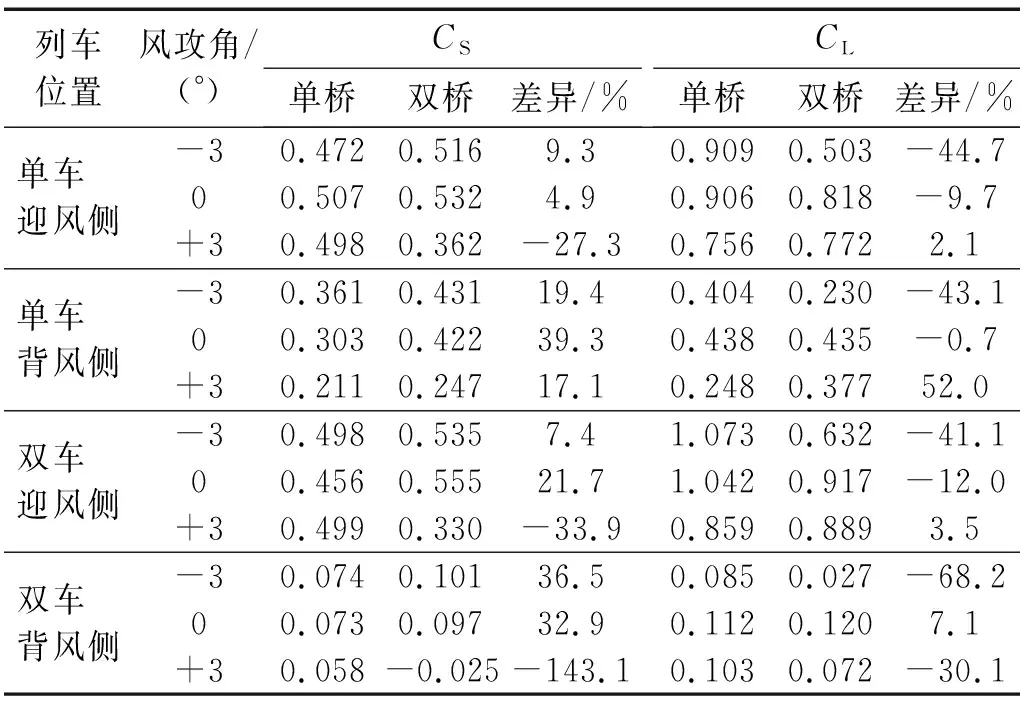
表2 列车气动力系数Tab.2 Three-component coefficients of vehicle

由表3可知，受既有桥梁影响，不同工况下桥梁的阻力系数均减小，且减幅随着风攻角的增大而增大，升力矩系数基本均增大；其中，+3°风攻角桥面无车情况下阻力系数减幅最大，为-22.4%；0°风攻角桥面无车情况下升力矩系数增幅最大，为200.6%。当风攻角为-3°时，不同工况下桥梁的升力系数均增大，最大增幅为29.2%；其余风攻角下桥梁升力系数的变化规律不明显。

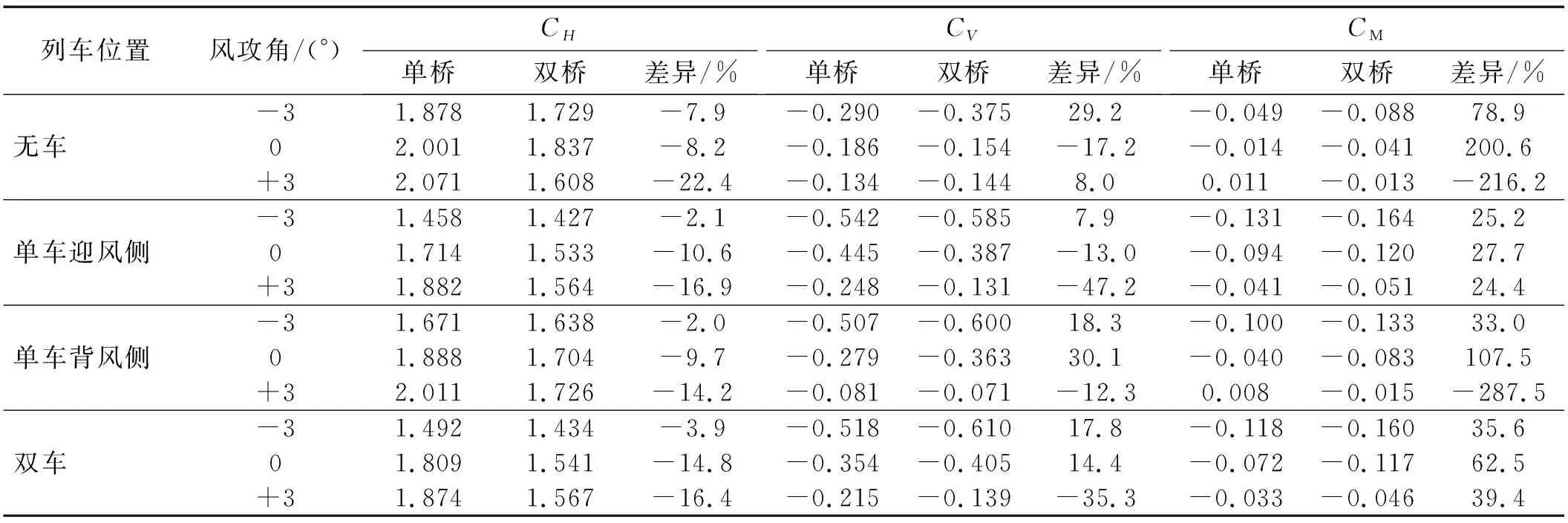
表3 桥梁气动力系数Tab.3 Three-component coefficients of bridge

综上所述，受既有桥梁影响，相邻车-桥系统的气动力系数变化明显，表明既有桥梁对邻近车-桥系统的气动干扰效应显著，且部分工况下列车、桥梁的气动力系数大幅增大，对结构的整体抗风性能不利。因此，结构设计中应充分考虑既有桥梁对邻近新建车-桥系统静风荷载的影响。受既有桥梁干扰，相邻车-桥系统中列车的气动力系数变化幅度相对较大，表明桥上列车的静风荷载受既有桥梁的影响更大。

4 车-桥系统抖振力影响分析

4.1 风场模拟

由列车、桥梁的抖振力表达式可知，桥梁抖振力与顺风向和竖向脉动风有关，列车抖振力与顺风向、横风向和竖向脉动风有关。为了研究既有桥梁对邻近车-桥系统抖振力的影响，首先需要模拟相对于静止桥梁和移动列车的脉动风场。

模拟相对于桥梁的脉动风场较为容易，但是列车是移动的，模拟相对于移动列车的脉动风场则较为复杂。常用方法是沿顺桥向模拟大量离散的脉动风场，然后插值选取不同位置风场不同时刻的脉动风速值构造出相对于移动列车的脉动风场。当模拟点数量线性增加时，计算量则呈指数型增长，使用该方法模拟移动列车时程计算量大、效率低。此外，插值选取风速值将导致构造的移动列车脉动风时程不连续而产生“突变”。另一种方法是使用相对于移动列车的脉动风谱，直接模拟相对于移动列车的脉动风时程，避免模拟大量离散风场，可有效减少计算量[14-15]。

本文采用Yan等推导的相对于移动列车的脉动风谱

(14)

(15)

Sξξ(Δy,f)=Cohξ(Δy,f)Sξ(f)

(16)

式中：Sξ′ξ′(Δη,f)为相对于移动列车风场的互谱，ξ=u,v,w；Rξ′ξ′(Δη,τ)为相对于移动列车风场的互相关函数；Sξξ(Δy,f)为相对于脉动风互谱；Sξ(f)为常用脉动风自谱；Cohξ(Δy,f)为风场相干函数；τ′=Δx/U为时间间隔，其中Δx=(Vtrτ-Δη)cosφ0， Δy=(Vtrτ-Δη)sinφ0； Δη为列车上风场模拟点间距；φ0为平均风速与车速的夹角，当风速垂直于列车运行方向时φ0=90°。当Δη=0时，式(14)便为相对于移动列车的脉动风场自谱。

将顺风向和横风向Simiu谱、Lumley-Panofsky竖向风谱和Davenport相干函数代入上述公式，便可得到对应风环境下相对于移动列车的风谱。取风速U=25 m/s、车速Vtr=80 km/h，时间步长Δt=0.25 s，风向角φ0=90°，通过谐波合成法分别模拟相对于桥梁和移动列车的脉动风时程，如图4、图5所示。

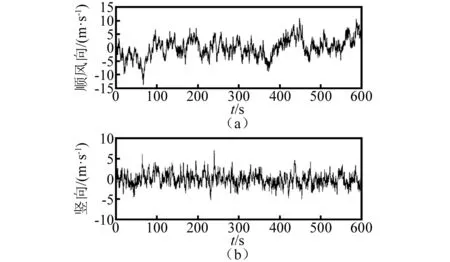
图4 相对于桥梁的脉动风时程Fig.4 Time histories of turbulence relative to bridge

图5 相对于移动列车的脉动风时程Fig.5 Time histories of turbulence relative to moving vehicle

4.2 移动列车抖振力时程

为了简化研究，列车、桥梁的导纳函数取1.0。基于上述模拟的脉动风场，分别模拟考虑、不考虑既有桥梁影响工况下单车、双车过桥时作用在列车、桥梁上的抖振力。桥上无车、单车、双车情况下，车-桥系统抖振力时程的影响如图6～图9所示。

图6 单车过桥时移动列车的抖振力Fig.6 Buffeting forces of moving vehicle as one vehicle moving on bridge

由图6、图7可知，受既有桥梁影响，单车/双车过桥时，迎风侧列车抖振横向力、抖振升力幅值均显著增大；背风侧列车的抖振横向力幅值略有增大。其中，单车情况下，背风侧列车抖振升力幅值略有减小；双车情况下，背风侧列车抖振升力幅值基本不变。

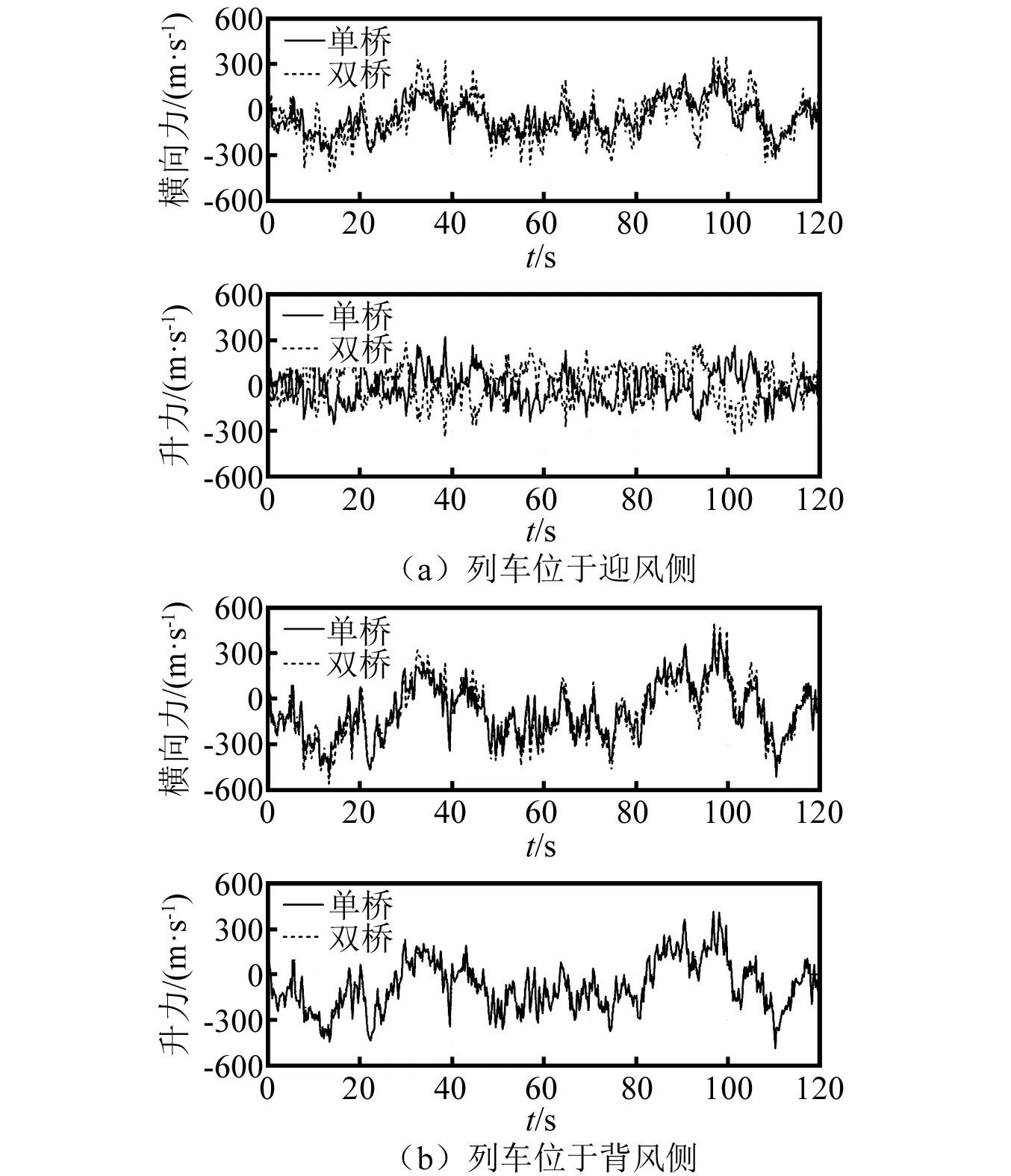
图7 双车过桥时移动列车的抖振力Fig.7 Buffeting forces of moving vehicle as two vehicles moving on bridge

由图8、图9可知，受既有桥梁影响，各工况下相邻桥梁的抖振阻力幅值均减小，抖振升力和升力矩的幅值略有增大。由图8、图9可知，当桥上有车时，作用在桥梁上的抖振力升力、升力矩幅值显著大于桥上无车工况下的，表明列车对桥梁产生影响，导致作用在桥梁上的抖振升力、抖振升力矩增大。

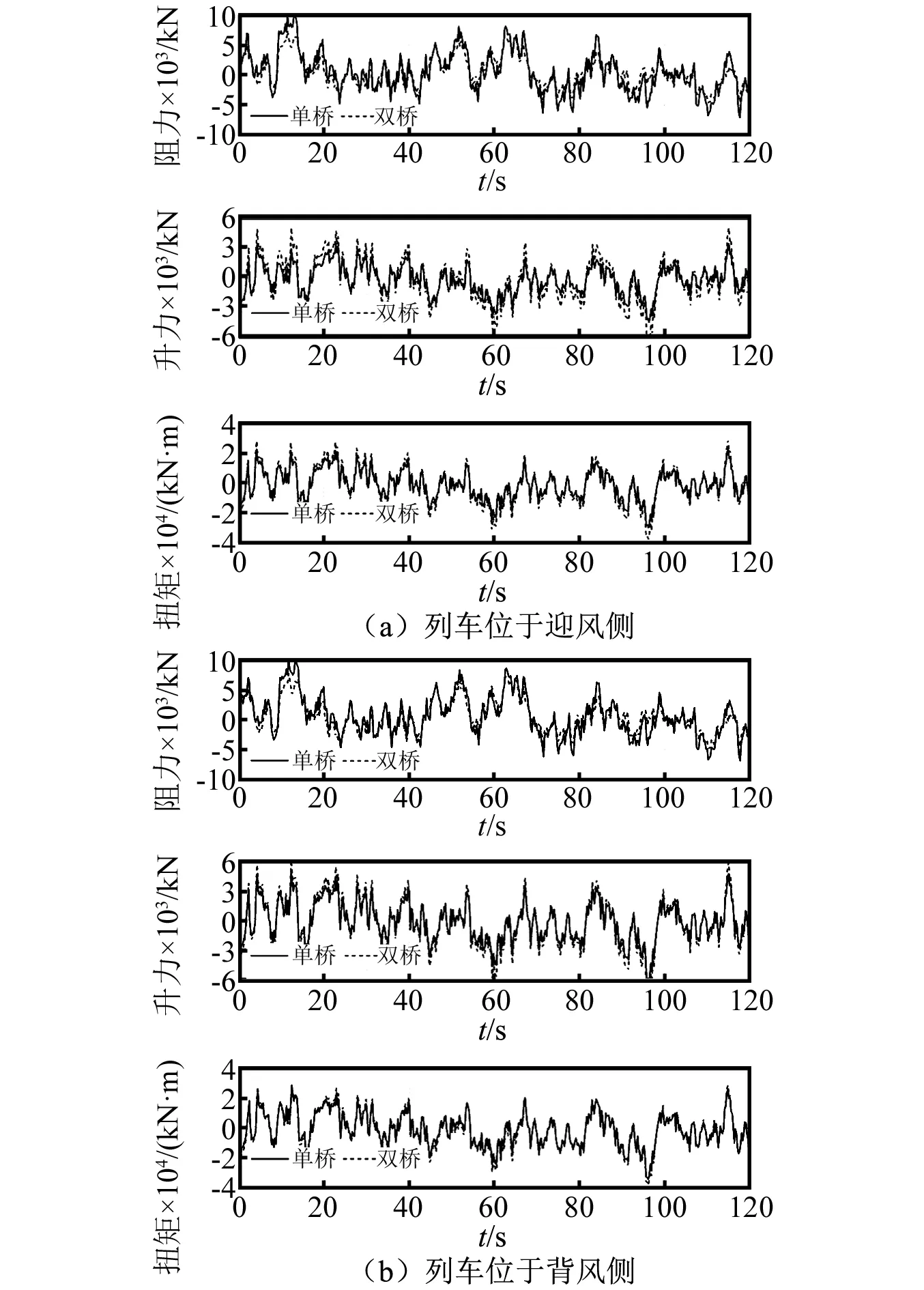
图8 单车过桥时桥梁的抖振力Fig.8 Buffeting forces of bridge as one vehicle moving on bridge

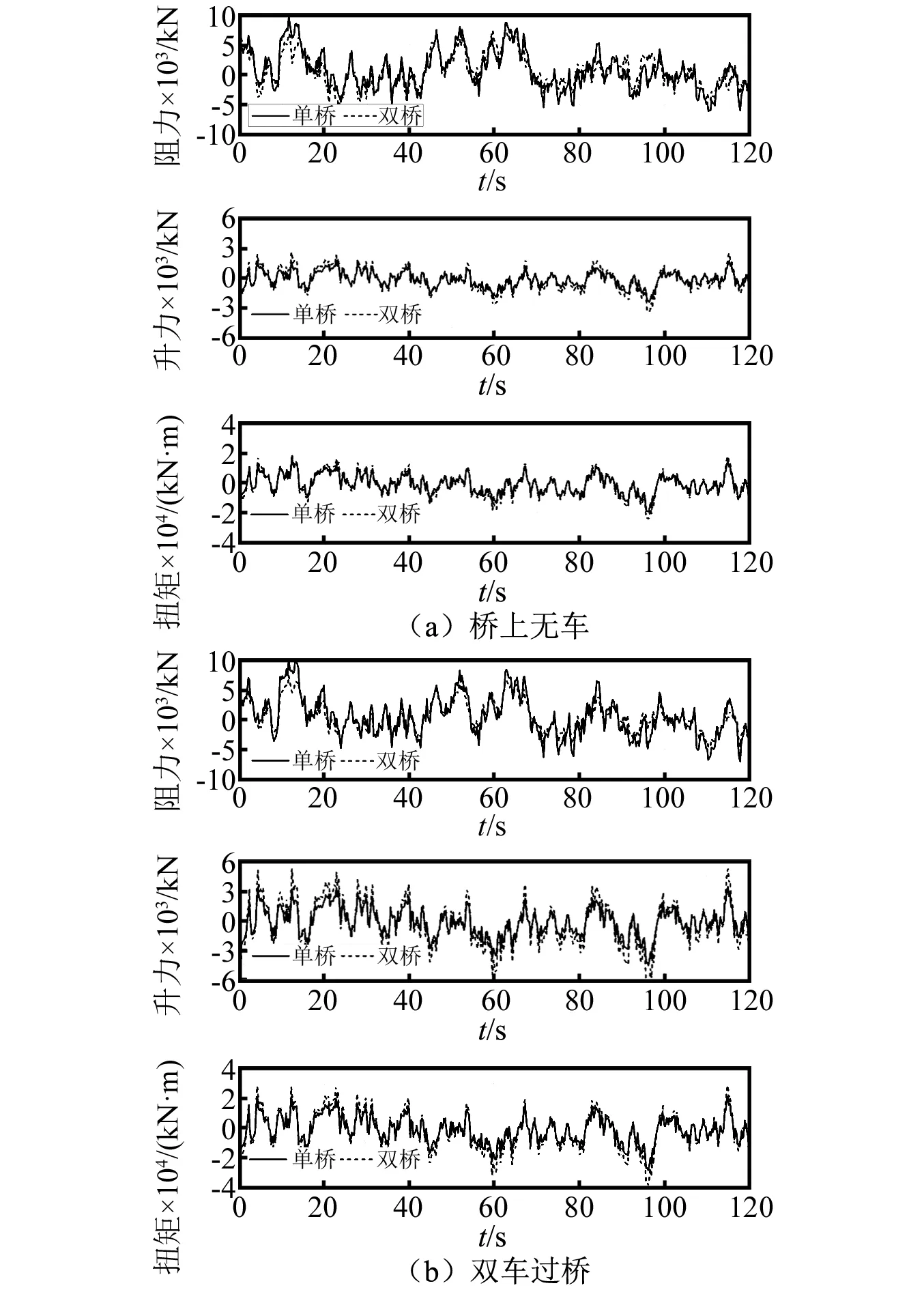
图9 桥上无车、双车过桥时桥梁的抖振力Fig.9 Buffeting forces of bridge as no vehicles or two vehicles moving on bridge

综上所述，既有桥梁对相邻桥梁上迎风侧列车抖振力的影响显著，且抖振力幅值受既有桥梁的影响而显著增大；背风侧列车抖振力受到的影响相对较小，其中，抖振横向力幅值略有增大，抖振升力基本不变。较之桥上列车，邻近桥梁受既有桥梁影响相对较小，其中抖振阻力幅值均减小，抖振升力和升力矩幅值略有增大。

4.3 抖振力极值

横向风作用下，车-桥系统响应极值主要受风速极值控制，即脉动风极值。研究中通常将脉动风视为各台历经零均值的平稳高斯过程，则抖振力也为各台历经零均值的平稳高斯过程。零均值平稳随机过程的极值服从穿越率基于泊松假定的极值概率分布，则时长T内不同超越概率下抖振力极值可以表示为

(17)

(18)

(19)

式中：Fmax为超越概率pf下抖振力的极值，即抖振力大于Fmax的概率为pf；v0为穿越率；λn为抖振力谱SF(f)的第n阶矩。

为了进一步研究既有桥梁对邻近桥梁车-桥系统抖振力极值的影响，取时长T=10 min，分别计算5%超越概率下上述工况列车、桥梁抖振力的极值，计算结果如表4、表5所示。

由表4可知，受既有桥梁影响，相邻桥梁上迎风侧列车抖振力极值显著增大；背风侧列车抖振横向力极值略有增大，抖振升力极值略有减小。其中，双车情况下迎风侧列车抖振横向力增幅最大，为35.2%；单车情况下迎风侧列车抖振升力增幅最大，为67%。

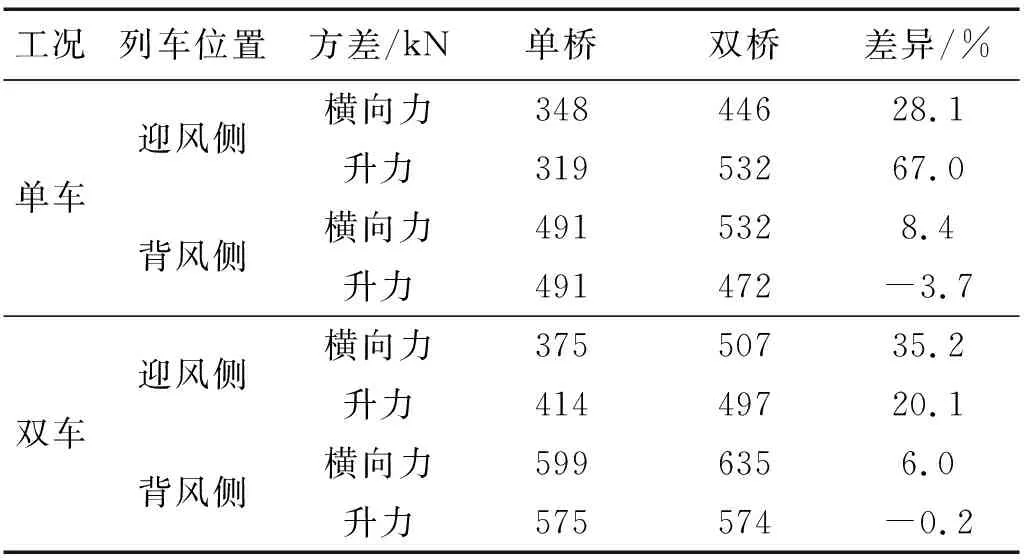
表4 列车抖振力极值Tab.4 Exreme values of buffeting forces of vehicle

由表5可知，受既有桥梁影响，不同工况下相邻桥梁抖振阻力极值均减小，抖振升力和抖振升力矩极值均增大，且抖振升力极值增幅最大。通过对比可知，桥上有车时，相邻桥梁抖振阻力极值受既有桥梁干扰而减小的幅度比桥上无车工况下的小，表明桥上有车时，既有桥梁对相邻桥梁抖振阻力的干扰效应大于无车情况下的。双车情况下，相邻桥梁的抖振力极值变化幅度最大，抖振阻力减小22.9%、抖振升力增大48.5%、抖振升力矩增大37.5%，表明双车过桥时桥梁抖振力极值受既有桥梁的影响最大。

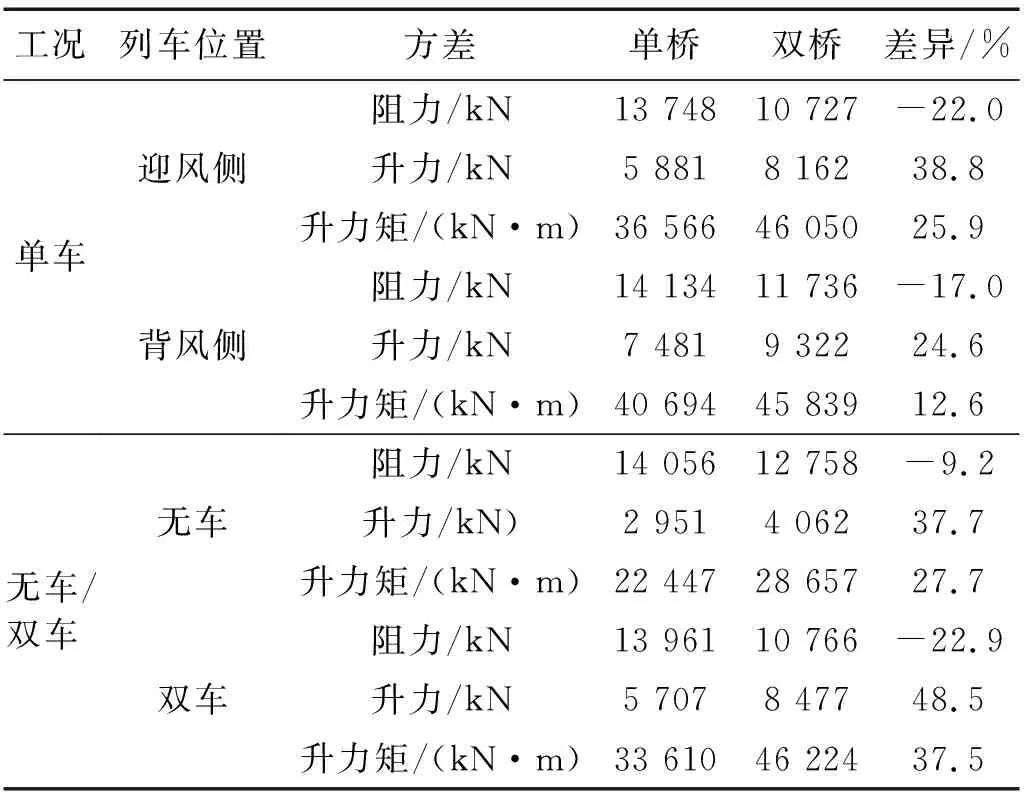
表5 桥梁抖振力极值Tab.5 Extreme values of buffeting forces of bridge

综上所述，车-桥系统抖振力极值受既有桥梁的干扰显著。受既有桥梁的影响，除了背风侧列车抖振升力和桥梁抖振阻力的极值减小，车-桥系统其余抖振力极值均显著增大。因此，结构设计中应充分考虑既有桥梁对相邻车-桥系统抖振力的影响。

5 结 论

通过节段模型风洞试验、数值模拟，本文研究了既有桥梁对相邻车-桥系统气动力的影响，得到以下结论：

(1) 既有桥梁对相邻车-桥系统气动力影响显著，会导致部分工况下列车、桥梁的气动力系数、抖振力显著增大，对结构的整体抗风性能不利，结构设计过程中应该充分考虑既有桥梁对邻近新建车-桥系统气动力的干扰效应。

(2) 既有桥梁对相邻车-桥系统气动力的影响与列车的位置、风攻角有关，并呈现一定的变化规律。其中，列车的气动力系数、抖振力受既有桥梁的影响更为显著。

(3) 受既有桥梁影响，迎风侧列车抖振力幅值均显著增大，背风侧列车的抖振力幅值变化较小。相邻桥梁的抖振阻力幅值减小，抖振升力和升力矩的幅值增大。

(4) 车-桥系统抖振力极值受既有桥梁的干扰显著。受既有桥梁的影响，除了背风侧列车抖振升力和桥梁抖振阻力的极值减小，车-桥系统其余抖振力极值均显著增大。