车轮谐波磨耗对轮轨蠕滑特性的影响分析

吴 丹， 丁旺才， 郭富强， 马 琳

(1. 兰州交通大学 机电工程学院，兰州 730070； 2. 中国铁路成都局集团有限公司成都动车段，成都 610051)

目前，高速列车车轮多边形问题日益凸显，而车轮谐波磨耗是车轮多边形最主要的表现形式，普遍存在于高速列车和地铁车辆中[1-3]，造成车辆轮轨关系恶化，对铁路系统的安全运行构成极大威胁，对高速列车影响更大。1998年，德国ICE高速列车脱轨，造成人员伤亡的重大事故，事故原因就是多边形橡胶弹性轮的接触载荷过大，导致车轮轮辋断裂[4]。针对车轮谐波磨耗产生的机理以及所引发的高频振动，国内外学者做了大量的研究，对机理的研究目前尚没有统一的定论[5]。Wu等[6]基于实测试验研究车轮多边形的形成机理，表明构架耦合共振主导了车轮多边形的形成。刘韦等[7]通过建立刚柔耦合车辆系统动力学模型，表明柔性轮对能更真实地反映轮对振动和轮轨力的变化，并应尽量避免车轮多边形产生的激励与柔性轮对垂直弯曲振动频率耦合所对应的运行速度。Xiao等[8]基于UM软件建立CRH2型车辆-轨道耦合模型，研究发现谐波阶次和波深幅值对轮对横向位移的影响不大，且波深影响大于阶次，并发现最大接触角和等效锥度均出现在谐波磨耗的最深处。Wu等[9]基于SIMPACK软件建立柔性轮轨模型，研究了车轮多边形对高速列车动力响应的影响，表明车轮谐波磨耗会使轮轨接触处产生高频冲击载荷，并激发轮对及轴箱的振动模态，引发共振，从而使轴箱加速度及应力过大。Zhao等[10]通过复特征值分析法研究了车轮多边形的形成机理，发现轮轨间的蠕滑力达到饱和时，可引起轮轨系统的摩擦自激振动，该振动是引发车轮多边形磨损的主要原因。Johansson等[11]根据轮轨接触FASTSIM算法，建立多体系统轮轨耦合模型，通过数值迭代模拟时域内的轮轨动态相互作用，并以某地铁车为例，分析车轮不圆度对轮轨动态特性的影响。Johansson等[12]通过现场试验和数值模拟研究了不同类型严重踏面损伤的货车的动力学响应，分析了车轮不圆度对轮轨垂向接触力和轨道响应的影响。崔大宾等[13]通过SIMPACK软件建立考虑真实车轮非圆化状态的车辆动力学模型，分析了车轮非圆化对车辆动力行为的影响。宋志坤等[14]通过SIMPACK软件和ANSYS软件建立柔性轮轨下的车辆-轨道耦合模型，分析了钢轨波磨和车轮谐波磨耗共同作用下对车辆振动特性的影响。胡晓依等[15]基于柔性轮轨模型，分析了阶次和幅值对车辆振动特性的影响。已有的研究多是研究车轮谐波磨耗对车辆动力响应的影响，鲜有研究考虑车轮谐波磨耗对轮轨接触特性的影响，但车轮谐波磨耗必然会造成轮轨接触斑内蠕滑特性的改变，而轮轨间的纵向蠕滑力对列车的牵引和制动性能起决定作用，横向蠕滑力也直接影响列车的横向稳定性和脱轨安全性。因此，研究车轮谐波磨耗对轮轨接触斑内蠕滑特性的影响具有非常重要的意义。

本文以CRH380D型高速动车组为研究对象，通过建立4种不同轮轨关系的车辆-轨道耦合动力学模型，结合多体动力学理论，分析最能反映真实情况的轮轨模型，并基于柔性轮轨关系下的车辆-轨道耦合动力学模型，系统分析了车轮谐波磨耗对轮轨接触蠕滑特性的影响，并在车轮谐波磨耗下进一步探究了轨下扣件参数和运行速度对蠕滑特性的影响。

1 车轮谐波磨耗测试及分析

采取接触式直接检测方法对车轮谐波磨耗进行测试，采用德国Müller-BBM公司生产的WMR 78661-h0型车轮粗糙度测试仪，根据测试仪的相关操作要求进行车轮谐波磨耗测试，其测试现场如图1所示。

图1 测试仪器及现场Fig.1 Test instrument and field

测量时，将测试仪固定在钢轨上方，并缓解轮轴制动力，保证车轮可绕车轴中心自由转动。经测试，得到了镟后15万km的谐波磨耗实测结果，车轮谐波磨耗实测结果的极坐标幅值图，如图2所示。可见左侧4位车轮均出现了明显的谐波磨耗，将实测结果通过HHT-希尔伯特黄变换处理可以得到阶次幅值图，如图3所示。从图3可知，4位车轮在第18阶均出现了粗糙度幅值明显增大的现象，可以得出车轮谐波磨耗主要是由第18阶所主导的。因此，在实际仿真计算中，可以将实际谐波磨耗处理成由第18阶主导的单一谐波激励。

图2 车轮谐波磨耗极坐标图Fig.2 Polar diagram of harmonic wear of wheel

图3 车轮谐波磨耗阶次图Fig.3 Order diagram of harmonic wear of wheel

2 车辆-轨道耦合动力学模型

2.1 轮对的柔性化

应用有限元软件ANSYS建立轮对的有限元模型，利用柔性模块FEM(finite element method)将轮对柔性体导入到车辆系统动力学模型中，选取2个界面节点，通过Craig-Bampton算法求解轮对的固有模态和静模态。计算轮对的前15阶模态及振型，其主要的模态和振型如表1所示。轮对4阶垂向弯曲模态如图4所示。

表1 轮对的主要模态Tab.1 Main modes of wheelset

图4 轮对4阶垂向弯曲模态Fig.4 The fourth order vertical bending mode of the wheelset

2.2 轨道的柔性化

柔性轨道模型是一种包括柔性钢轨、扣件、轨枕和道床的三维轨道模型。钢轨建立为梁单元有限元模型，扣件被模拟成Bushing力元类型的特殊力。

柔性轨道模型如图5所示。图中： ①为钢轨；②为扣件；③为轨道板；④为弹性体基础(路基)；kph，cph分别为轨下垫层及扣件对应的横向刚度和阻尼；kpv，cpv分别为轨下垫层及扣件对应的垂向刚度和阻尼；kbh，cbh分别为路基对应的横向刚度和阻尼；kbv，cbv分别为路基对应的垂向刚度和阻尼。

图5 柔性轨道模型拓扑图Fig.5 Topology of flexible track model

2.3 车辆-轨道耦合动力学模型的建立

为探究4种轮轨模型在车轮谐波磨耗作用下的动力学特性，建立刚性轮轨、刚性轮柔性轨、柔性轮刚性轨以及柔性轮轨共4种车辆-轨道耦合动力学模型，上述刚性轨为传统意义上所谓的“刚性轨道”，即不考虑钢轨及轨下基础的振动与变形，刚性轨道模型退化为保留轨头几何廓形的边界。通过对比分析，研究得到最能真实反映轮轨振动特性的模型，其中柔性轮轨下的车辆-轨道耦合动力学模型如图6所示。采用力元来模拟模型中各部件之间的连接关系。车辆动力学模型的基本参数、悬挂参数以及转动惯量参数均与该车实际参数一致，车辆动力学模型采用S1002CN车轮踏面，其主要参数，如表2所示。

图6 车辆-轨道耦合动力学模型Fig.6 Vehicle-track coupling dynamic model

表2 车辆动力学模型主要参数Tab.2 Main parameters of vehicle dynamics model

3 车轮谐波磨耗下轮轨关系模型的选择

为分析不同轮轨关系之间的差异，研究最能真实准确反映实际情况的轮轨关系模型，设置轨道长度为1 000 m，则柔性轨道的轨枕数目应为1 667根。设定车速为300 km/h，车轮谐波磨耗阶次为18阶，幅值为0.02 mm，以我国TB/T 3352—2014《高速铁路无砟轨道不平顺谱》中提供的计算方法计算所需轨道不平顺谱，并将其作为轨道激励输入，得到1位轮对左轮的轮轨垂向力时域图和频域图，如图7、图8所示。

图7 不同轮轨关系的轮轨垂向力频域图Fig.7 Frequency domain diagram of vertical force of wheel-rail with different wheel-rail relations

图8 不同轮轨关系的轮轨垂向力时域图Fig.8 Time domain diagram of vertical force of wheel-rail with different wheel-rail relations

车轮谐波磨耗产生的轮轨激励频率可通过式(1)进行计算

(1)

式中：N为车轮谐波磨耗阶次，取18阶；v为车速，取300 km/h；D为车轮滚动圆直径，取920 mm。

通过计算可得，18阶车轮谐波磨耗产生的轮轨激励频率为519 Hz。由图7可知，轮轨垂向力的主频为519 Hz，与采用式(1)计算得到的激扰频率一致。结合图7和图8，对不同轮轨关系的动态响应做进一步分析可知：同为刚性轨时，刚轮和柔轮的轮轨垂向力分别为88.32 kN，96.90 kN，考虑柔性轮对后轮轨垂向力增幅为9.7%；同为柔性轨时，刚轮和柔轮的轮轨垂向力分别为74.79 kN，84.13 kN，考虑柔性轮对后轮轨垂向力增幅为12.5%。由此发现，柔性轮下的轮轨垂向力均高于刚性轮，柔性轨下的轮轨垂向力均低于刚性轨。由于柔性轮对的4阶弯曲频率521 Hz与18阶谐波磨耗产生的轮轨激励频率519 Hz接近，触发了柔性轮对的4阶弯曲振动模态，因此柔性轮下的轮轨垂向力均高于刚性轮。根据崔大宾等的研究得出钢轨垂向pin-pin弯曲共振频率超过900 Hz，远高于车轮谐波磨耗所引起的轮轨激励频率，不会引起共振，同时，柔性轨相较于刚性轨可以有效的缓解轮轨间的高频冲击振动，因此柔性轨下的轮轨垂向力均低于刚性轨。轮对振动加速度的频域和时域分析也表现出了上述规律，由于篇幅所限，其频域图和时域图文中将不再呈现。

钢轨振动加速度的频域图，如图9所示。从图9中也可以得出上述规律。钢轨振动加速度的时域图，如图10所示。分析图10可知刚性轨的振动加速度存在近似等幅振荡。这是由于在数值计算中刚性轨被视为每个车轮下的刚性体，其计算点始终跟随于轮轨接触的下方，故会出现近似等幅振荡。而柔性轨的振动加速度整体呈现出先增大后减小的趋势，这是由于前轮通过后钢轨振动加速度会呈现衰减状态，直到后轮通过后才完全衰减，但柔性轮与柔性轨耦合时，车轮谐波磨耗产生的激励频率激发了轮对的4阶弯曲振动模态，从而使柔性轨的振动加剧，因此柔性轨的振动加速度出现在第二个峰值点，此后完全衰减。

图9 不同轮轨关系的钢轨振动加速度频域图Fig.9 Frequency domain diagram of vibration acceleration of track with different wheel-rail relations

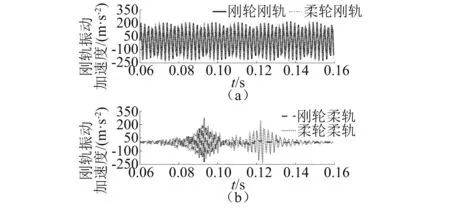
图10 不同轮轨关系的钢轨振动加速度时域图Fig.10 Time domain diagram of vibration acceleration of track with different wheel-rail relations

由此可知，在分析车轮谐波磨耗阶次、波深幅值以及扣件刚度和运行速度对轮轨蠕滑特性的影响时，考虑轮轨均为柔性体，可使计算结果更加准确，切合实际。

4 柔性轮轨下的蠕滑特性分析

4.1 轮轨蠕滑率/力推导

当轮轨间的蠕滑力小于极限摩擦力时，轮轨接触处于蠕滑状态，反之，处于纯滑动状态。正是由于蠕滑的存在，使车轮的圆周速度大于或小于前进速度，进而在轮轨间产生牵引力和制动力。由于考虑车轮谐波磨耗的轮轨在接触瞬间会发生较大的弹性变形，将直接影响轮轨接触位置以及接触斑内的蠕滑特性，故无法用解析法计算蠕滑力，需采用FASTSIM插值数表进行轮轨蠕滑力的求解。在该算法中，Kalker[16]简化理论用Winkler弹性基础代替精确理论中的弹性半空间，沿滚动方向接触斑的前沿向后沿进行链式求解，该理论认为稳态工况下，在接触区内实际滑动速度为0，其滑动方程为

(2)

引入轮轨接触表面的线性柔度系数Li，由此，弹性位移u和切向力p的关系，可表示为

ui=Li·pi(i=x,y)

(3)

将式(3)代入式(2)，并对式(2)进行积分得

(4)

(5)

因此，蠕滑力可通过应力在椭圆形接触斑内的积分得到，即

(6)

据Kalker线性理论的蠕滑率/力关系表达式为

(7)

根据Kalker滚动接触理论的基本方程可得到不考虑轮对摇头角速度和横移速度的蠕滑率ξx，ξy，φ的计算公式

ξx=(|v|-|c|)/v

(8)

ξy=sinψ≈ψ

(9)

φ=ωsinδ/V=sinδ/r0

(10)

式中：v为车轮接触斑上的滚动速度；c为圆周速度；ω为车轮滚动角速度；δ为接触角；ψ为轮对摇头角；r0为车轮名义滚动圆半径。

该简化计算公式由于忽略了很多因素往往仅用于机理研究，对于动力学数值仿真计算，需要建立更完整的蠕滑率计算公式。通过建立3组笛卡尔坐标系表征轮轨系统[17]，如图11所示。坐标系x′y′z′为体坐标系，其原点在轮对的质心。坐标系x″y″z″为中间坐标系，它通过绕z‴轴旋转ψ角后得到。坐标系x‴y‴z‴为平衡坐标系，其原点在轨道中心线上，且相对于固定的绝对坐标系xyz以等速度v前进，其中绝对坐标系xyz固定在轨道中心线上，φ为绕x″轴的侧滚角，ψ为绕z″轴的摇头角。此外，再建立2个瞬时性的轮轨接触点坐标系e1le2le3l和e1re2re3r，如图12所示。δl和δr分别为左右轮轨接触角，rl和rr分别为左右车轮滚动圆半径。

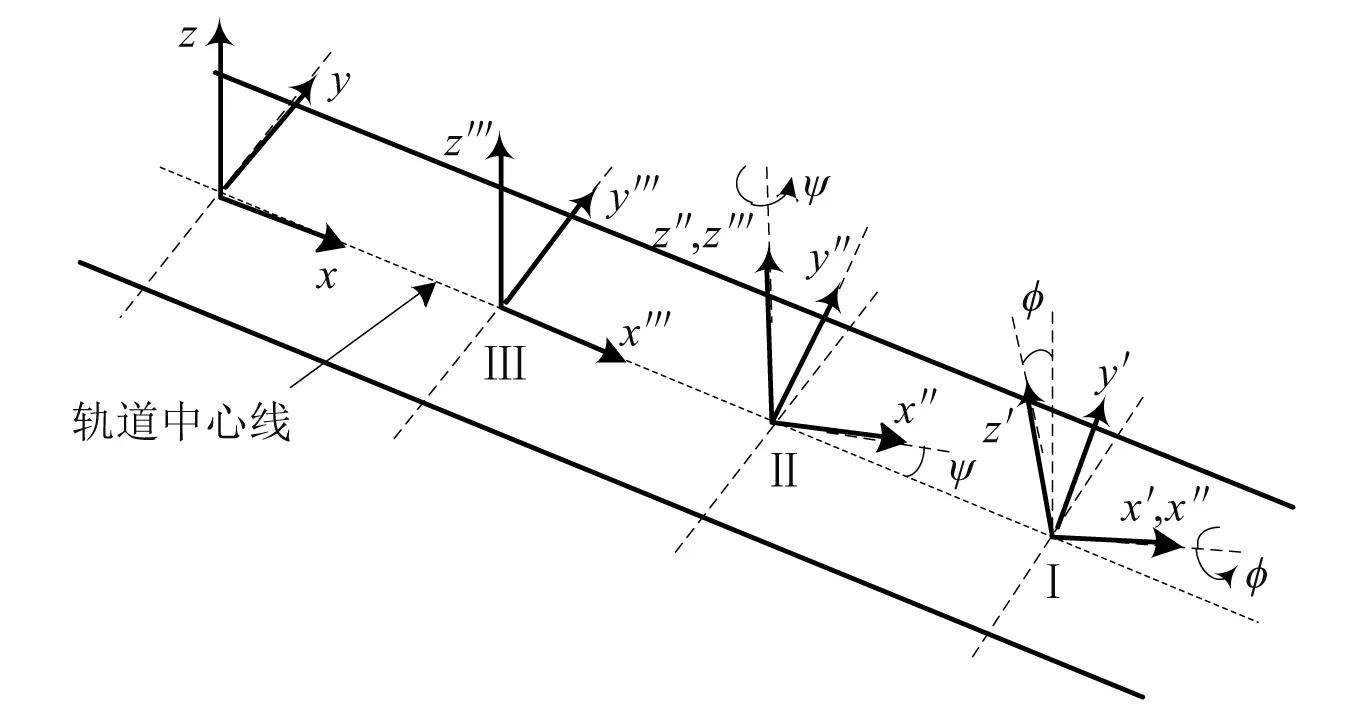
图11 坐标系Fig.11 Coordinate system

图12 接触点坐标系Fig.12 Contact point coordinate system

3组坐标轴之间的变换关系为

(11)

(12)

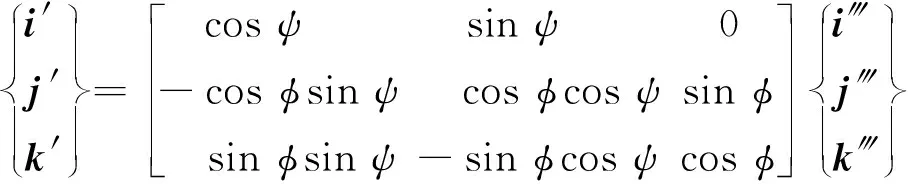
(13)

轮轨接触点坐标系同轮对体坐标系之间的变换关系为

(14)

(15)

轮对角速度ω的运动方程可在坐标系中推导得到，即

(16)

式(16)由式(11)进行坐标变换得

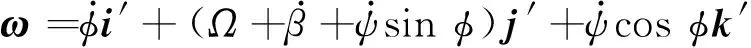
(17)

式中，β为绕y′轴名义角速度Ω的扰动角位移，且Ω=v/r0。

令Δl和Δr为轮轨接触点离开其平衡位置的横移量，Lw为轨距之半，则左右接触点的位置矢量以体坐标表示为

Rl=(Lw-Δl)j′-rlk′

(18)

Rr=-(Lw+Δr)j′-rrk′

(19)

式(13)以平衡坐标轴表示，左右位置矢量的分量为

(20)

(21)

R′l和R′r分别为左右接触点在平衡坐标系上的位置矢量，则

R′l=xi‴+yj‴+zk‴+Rl

(22)

R′r=xi‴+yj‴+zk‴+Rr

(23)

对R′l和R′r分别按时间求导，并略去高阶项后为

(24)

(25)

由蠕滑率的定义，即轮轨接触点处相对的线位移和角位移可得纵向蠕滑率、横向蠕滑率和自旋蠕滑率，分别为

(26)

(27)

(28)

对式(26)～式(28)进行化简，经代数运算并略去高阶项后得：

左侧车轮

(29)

(30)

(31)

右侧车轮

(32)

(33)

(34)

4.2 车轮谐波磨耗对蠕滑特性的影响

高速列车在运行过程中，其轮轨接触条件对轮轨间蠕滑特性影响很大，通过第3章分析得到车轮谐波磨耗会引起轮轨间的振动加剧，这势必影响轮轨间的接触条件，进而影响其蠕滑状态，加剧轮对自激振动，由文献[18]可知，轮对自激振动是产生车轮谐波磨耗的原因之一，因此轮轨之间会形成一种产生和激发轮轨高频振动的不良循坏，从而对蠕滑特性造成一定影响。

为探究车轮谐波磨耗对轮轨接触斑内蠕滑特性的影响，根据实测车轮谐波磨耗的数据，选取4种主要谐波阶次(3阶、6阶、9阶和18阶)和4种波深幅值(0.05 mm，0.10 mm，0.15 mm和0.20 mm)，基于最能真实反映实际情况的柔性轮轨下的车辆-轨道耦合模型对轮轨接触蠕滑特性进行对比研究，通过计算得到不同阶次和幅值下的纵向蠕滑率/力，如图13、图14所示。由图13可知，纵向蠕滑率整体呈现出随波深幅值和阶次增大而增大的趋势，且在高谐波阶次下，其波深幅值的影响更加明显，在低阶且幅值较小处，其对纵向蠕滑率的影响较无谐波磨耗时相差不大。在第18阶、0.2 mm幅值处的纵向蠕滑率最大，其纵向蠕滑率为无谐波磨耗(纵向蠕滑率为0.206 4%)的1.32倍。由图14可知，纵向蠕滑力同样呈现出随波深幅值和阶次增大而增大的趋势，且高阶次下波深幅值对纵向蠕滑力的影响较低阶次下更为明显。同样，在第18阶、0.2 mm幅值处的纵向蠕滑力最大，其纵向蠕滑力为无谐波磨耗(纵向蠕滑力为8.665 7 kN)的2.68倍。

图13 车轮谐波磨耗对纵向蠕滑率的影响Fig.13 Influence of harmonic wear of wheel on longitudinal creepage

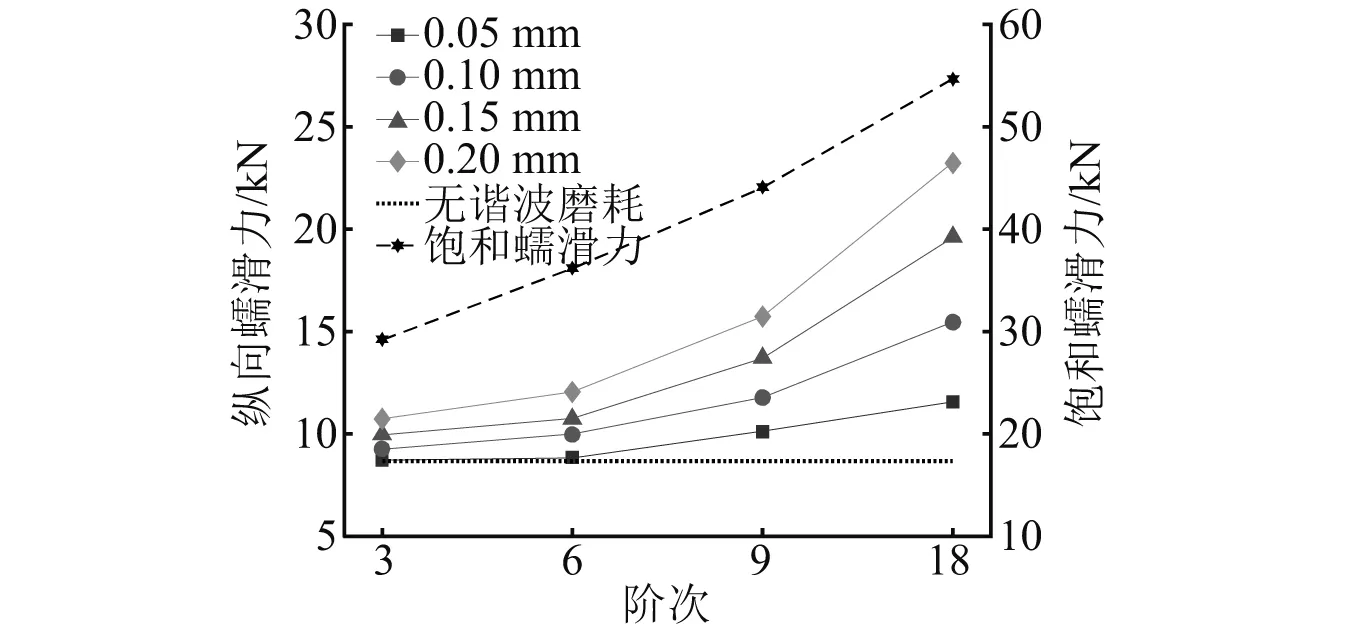
图14 车轮谐波磨耗对纵向蠕滑力的影响Fig.14 Influence of harmonic wear of wheel on longitudinal creep force

不同阶次和幅值下的横向蠕滑率/力如图15、图16所示。由图15可知，在低谐波阶次下，波深幅值对横向蠕滑率的影响要高于阶次的影响。但无论在低阶还是高阶都呈现出随波深幅值和阶次增大而增大的规律，在第18阶、波深幅值为0.2 mm处其横向蠕滑率最大，为无谐波磨耗(横向蠕滑率为0.137 5%)的2.13倍。由图16可知，当波深幅值较高时，阶次对横向蠕滑力的影响较低幅值下的影响更加显著，但整体同样呈现随波深幅值和阶次增大而增大的趋势，在第18阶、波深幅值为0.2 mm处，横向蠕滑力最大，其为无谐波磨耗(横向蠕滑力为8.086 1 kN)的1.57倍。

图15 车轮谐波磨耗对横向蠕滑率的影响Fig.15 Influence of harmonic wear of wheel on lateral creepage

图16 车轮谐波磨耗对横向蠕滑力的影响Fig.16 Influence of harmonic wear of wheel on lateral creep force

从计算数据可知，低阶处的纵向蠕滑率基本均约为0.2%，说明低阶处轮轨接触斑内黏着区占大部分，此时蠕滑力较小，轮轨黏着关系良好。但在第18阶、0.2 mm幅值下其纵向蠕滑率接近0.3%，此时接触斑内黏着区逐渐减少，滑动区逐渐扩大并占接触斑面积的大部分。其原因为18阶下的车轮谐波磨耗激励频率激发了轮对的4阶弯曲模态，加剧了轮轨振动，进而影响了轮轨之间的接触关系，使蠕滑率/力显著增大。

由于Kalker简化理论考虑了蠕滑力的饱和效应，即考虑了库伦摩擦力(轮轨间极限摩擦力)Tmax=f·p，p为接触面内法向力，f为轮轨间摩擦因数，取值为0.3。通过和饱和蠕滑力曲线对比发现，蠕滑力没有达到饱和，也就意味着轮对没有发生空转或滑行。

4.3 谐波磨耗下轨下参数和速度对蠕滑特性的影响

由第3章分析可知，车轮谐波磨耗会引发轮轨振动加剧，导致轮轨接触关系不良，而扣件刚度直接决定钢轨的振动特性和位移，由于车轮谐波磨耗不可避免，研究基于车轮谐波磨耗下的轨下参数，分析其影响规律，寻求通过轨下参数优化轮轨接触特性，以期改善轮轨接触状态。

由参考文献[19-20]可知，扣件刚度的范围为45～170 kN/mm，并考虑运行速度对蠕滑特性的影响，故本文选取扣件刚度范围为40～160 kN/mm，运行速度范围为150～350 km/h，基于第6阶、0.05 mm幅值下的车轮谐波磨耗，计算得到不同扣件刚度和运行速度对蠕滑特性的影响。

运行速度对纵向蠕滑特性的影响要明显大于扣件刚度的影响，如图17、图18所示。且从图17(b)、图18(b)状态参数分布图中可知：在低速区，其纵向蠕滑率/力随扣件刚度的增大而减小；在高速区，其纵向蠕滑率/力随扣件刚度的增大而增大。纵向蠕滑率/力在低速区受速度的影响并不敏感，但当速度高于250 km/h时，速度对蠕滑特性的影响极为显著。

图17 纵向蠕滑率Fig.17 Longitudinal creepage

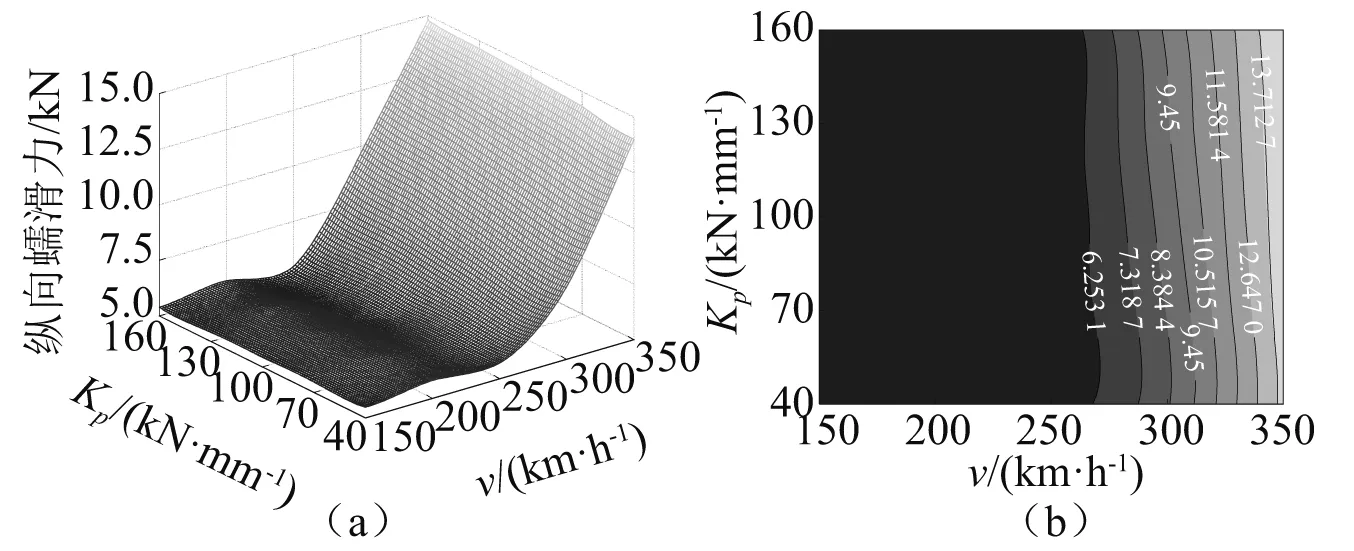
图18 纵向蠕滑力Fig.18 Longitudinal creep force

扣件刚度对横向蠕滑率/力的影响较纵向蠕滑率/力更显著，如图19、图20所示。同样，在低速区和高速区，横向蠕滑率/力随扣件刚度的增大呈现出相反的特性。但在低速区其影响波动较小，而在高速区影响较大。因此，要实现良好的轮轨接触特性，扣件刚度的取值不宜过大。

图19 横向蠕滑率Fig.19 Lateral creepage

图20 横向蠕滑力Fig.20 Lateral creep force

综上，相较于扣件刚度，运行速度对蠕滑特性的影响更明显。不同速度下的蠕滑力频域图，如图21、图22所示。究其原因，结合图21、图22做进一步分析可知，在相同的扣件刚度下，蠕滑力随着运行速度的提高，其振动频率有向高频区转迁的趋势，从而容易引发高频振动，促使轮轨振动加剧，导致轮轨接触关系恶化。因此，在车轮谐波磨耗激扰作用下，要实现良好的轮轨接触关系，速度应作为第一参考要素，且当速度高于300 km/h时，轨下扣件刚度参数的选取在考虑轨道变形和工程造价的前提下应尽量取低值。

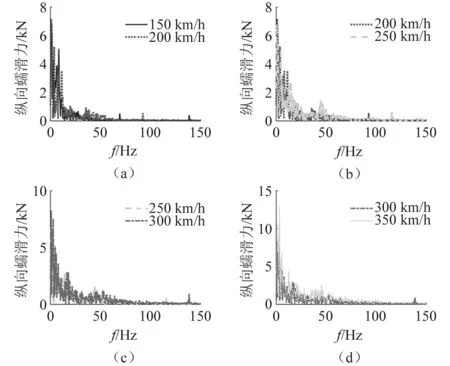
图21 不同速度下纵向蠕滑力频域图Fig.21 Frequency domain diagram of longitudinal creep force under different velocities

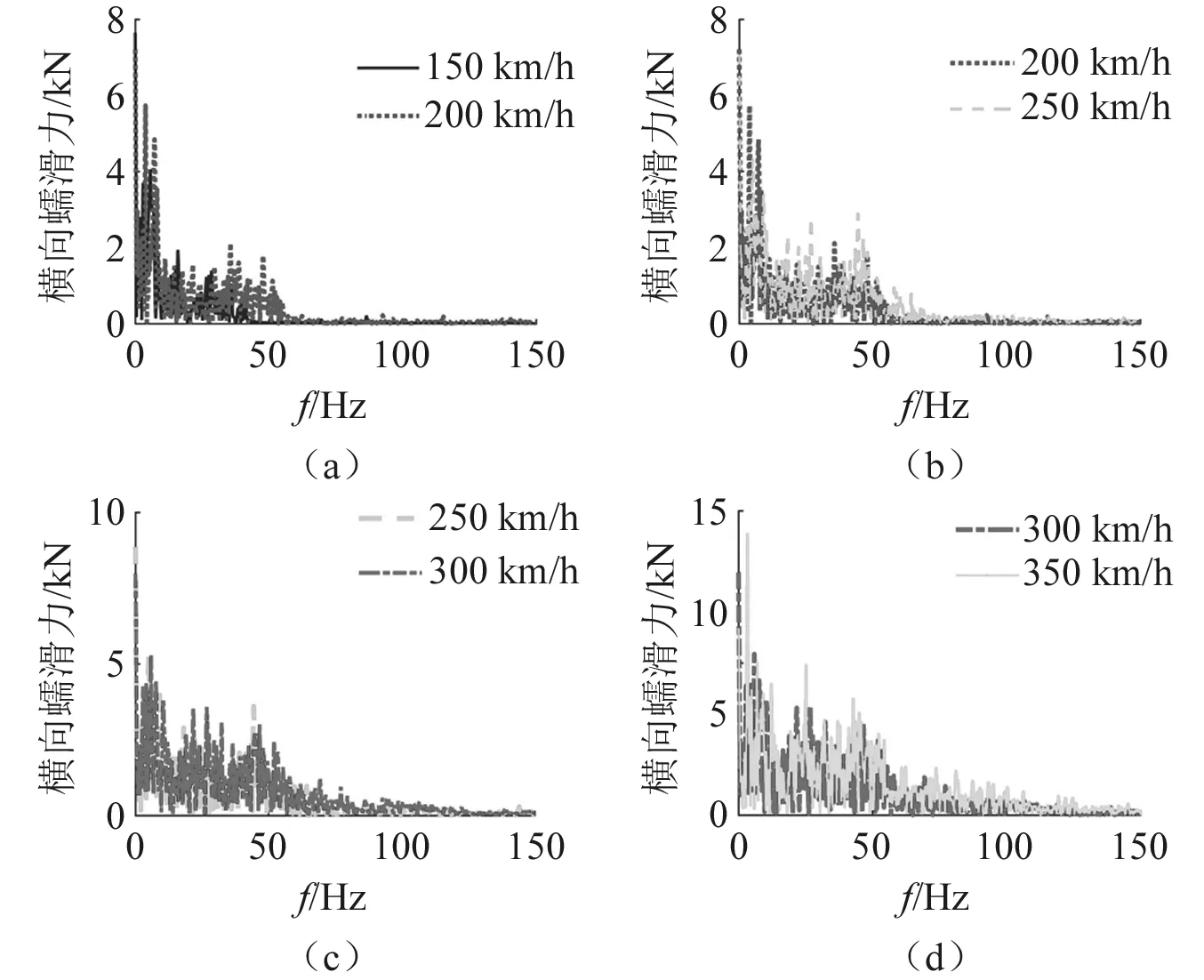
图22 不同速度下横向蠕滑力频域图Fig.22 Frequency domain diagram of lateral creep force under different velocities

5 结 论

通过建立4种不同轮轨关系的车辆-轨道耦合动力学模型，结合多体动力学理论，分析了4种轮轨关系下的振动响应，并基于柔性轮轨关系下的车辆-轨道耦合模型研究了车轮谐波磨耗、扣件刚度以及运行速度对轮轨间蠕滑特性的影响。主要结论有：

(1) 由第18阶主导的车轮谐波磨耗激励频率为519 Hz，与柔性轮对的4阶弯曲振动模态频率521.9 Hz接近，激起了轮对的4阶弯曲振动模态，引起系统振动加剧，导致柔性轮下的振动响应高于刚性轮；同时，钢轨的垂向pin-pin弯曲频率远高于谐波磨耗激励频率，加之柔性轨可以缓解轮轨间的高频冲击，使得柔性轨下的振动响应低于刚性轨。

(2) 车轮谐波磨耗的阶次和幅值对轮轨蠕滑率/力的影响显著，呈现出随阶次和幅值增大而增大的趋势，尤其在高谐波阶次下，幅值对蠕滑率/力的影响更加显著。高谐波阶次下的车轮谐波磨耗激励频率容易激发车轮的固有弯曲模态，加剧轮轨振动，进而影响轮轨之间的接触关系，使蠕滑率/力显著增大。

(3) 扣件刚度对蠕滑特性的影响与速度呈现相关性，当速度低于250 km/h时，扣件刚度对蠕滑率/力的影响并不显著，但仍呈现出随刚度增大而减小的趋势，当速度高于300 km/h时，扣件刚度对蠕滑率/力的影响比较明显，呈现出随刚度增大而增大的趋势。同一扣件刚度下，随速度的增大，其振动频率有向高频区转迁的趋势，从而容易引发高频振动，促使轮轨振动加剧，导致轮轨接触关系恶化。