基于可视图图谱幅值熵的滚动轴承故障诊断方法
陈 芒, 于德介, 高艺源
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
对机械振动信号进行特征提取是机械故障诊断的关键步骤[1]。目前,机械振动信号特征提取技术主要是基于传统的时域分析、频域分析、时-频域分析方法[2]。然而,由于滚动轴承故障振动信号的非平稳性和非线性,传统的信号处理方法往往难以有效地提取复杂的故障特征[3-4]。因此,有必要进一步研究有效的轴承故障特征提取方法。
近年来,图信号处理(graph signal processing,GSP)技术随着图谱理论的发展而迅速兴起,该项技术主要是将传统的信号处理方法拓展到图信号的分析处理。目前国内外学者先后提出了许多图信号处理方法,如图离散信号处理(discrete signal processing on graph,DSPG)、图傅里叶变换(graph Fourier transform,GFT)、图短时傅里叶变换(graph short-time Fourier transform,GSTFT)、图小波变换(graph wavelet transform,GWT)和图经验模态分解(graph empirical mode decomposition,GEMD)等[5-9]。目前,GSP技术已广泛应用于计算机网络、气候变化和图像处理等领域[10-11],然而该技术在机械故障诊断领域中的应用并不多见。
GSP方法与传统的振动信号处理方法不同,前者研究的是振动数据集关系的图结构,后者研究的是振动数据集本身[12]。复杂网络是一种特殊的图结构,对于非线性时间序列,复杂网络能更好地捕捉其动力学特征。可视图算法(visibility graph,VG)[13-16]是一种特殊的能将离散时间序列转变成复杂网络的算法。对于振动信号,其本身就是典型的离散时间序列,因此可以通过可视图建网方法将振动信号转变成可视图复杂网络,从而在复杂网络的顶点域、图谱域和顶点-图谱域对故障振动信号分析处理。近年已有一些学者初步研究了基于复杂网络顶点域的机械故障特征提取方法。孙斌等[17]针对离心泵振动信号的非线性及其非平稳特性,提出了一种基于可视图网络节点重要性度量的离心泵振动故障诊断方法。陈安华等[18]提出了基于复杂网络社团聚类的故障模式识别方法。
本文将复杂网络与GSP技术引入故障诊断领域,针对滚动轴承振动信号转变的可视图信号,在图谱域对故障振动信号分析处理。熵是一种描述系统不确定性程度的量,能够反映出系统中量的分布情况[19]。本文根据信息熵理论,定义了图谱幅值熵(graph spectrum amplitude entropy,GSAE),并将其作为滚动轴承的单一故障特征,提出了基于可视图图谱幅值熵(graph spectrum amplitude entropy of visibility graph,GSAEVG)和马氏距离(Mahalanobis distance,MD)[20]的滚动轴承故障诊断方法。应用实例表明,本文方法不仅能有效准确地识别滚动轴承不同故障,还能有效区分不同程度内圈故障,且区分效果明显优于基于传统的熵指标的故障诊断方法。
1 可视图
1.1 图的基本概念
一个无向、连通、加权图可用G=(V,E,W)来表示,其中:V为顶点的集合;E为边的集合;W为加权的邻接矩阵。 若vi和vj这2个顶点之间有边eij=(vi,vj)连接,那么这条边的权值就用wij来表示,若没有边连接,则wij=0。在实际应用中,wij通常由人为来设定,一般用以下3种方式来定义
W1∶wij=1
(1)
(2)
W3∶wij=‖xi-xj‖2
(3)
式中,xi和xj分别为顶点vi和vj的函数值。式(1)定义的权值都为1,完全忽视了顶点之间的差异;式(2)定义的权值均小于等于1,忽略了部分顶点之间的差异;式(3)定义的权值为两顶点之间的平方欧氏距离,可以如实反映顶点间的差异。
在邻接矩阵基础上,建立能更好反映图中蕴含在顶点之间关系的图拉普拉斯矩阵,定义为
L=D-W
(4)
式中,D为度对角矩阵,表示各顶点连接的边数,其对角元素为di=∑wij。
1.2 可视图建网算法
可视图建网算法中,网络中的每个节点与离散时间序列数据中的每个时间点对应 ,其基本思想如图1所示。在图1(a)中,用5个直方条表示一个离散时间序列的前5个数据点,直方条的高度表示每个时间点数值大小;图1(b)中的每个实点与时间序列中的数据顶点相对应,假如2个直方条的顶端相互可视,则对应的两点相连。可视性准则如下:
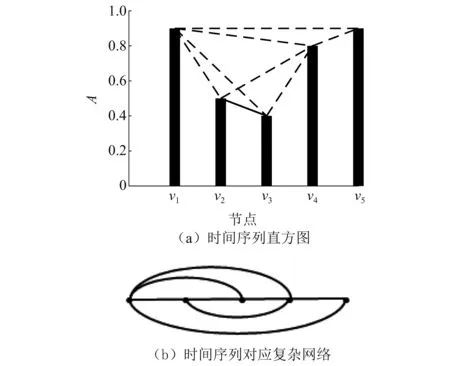
图1 时间序列可视图建网Fig.1 Visibility graph of time series
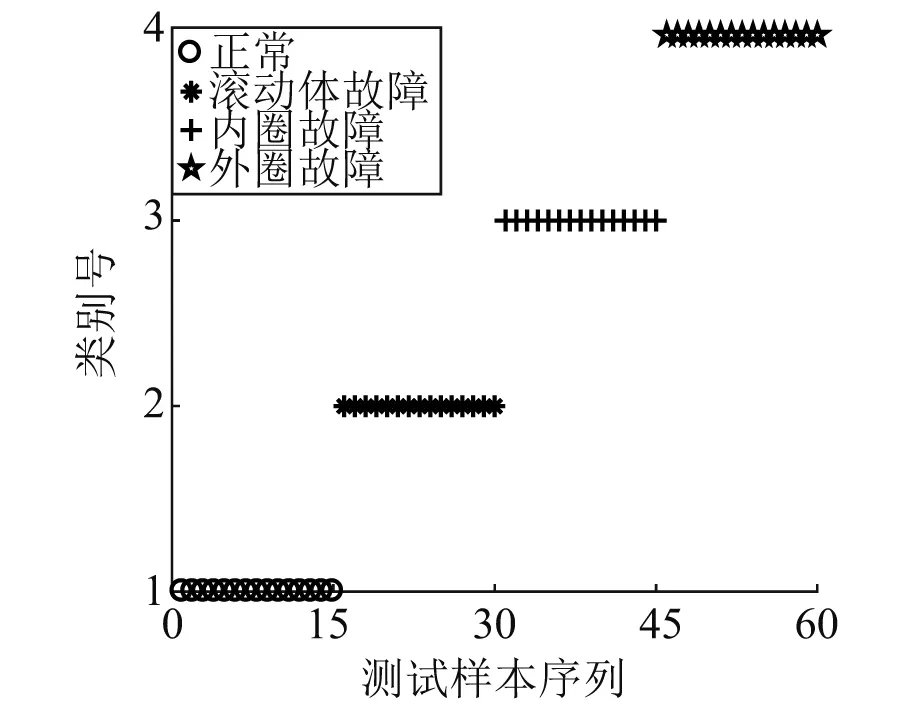
若离散时间序列中任意2个点(va,xa)与(vb,xb)相互可视,那么对任意点(vc,xc),其中va (5) 可视图算法建立的复杂网络有如下性质:①网络为无向网络;②每个点至少与其左右相邻的节点相连;③横轴及纵轴经过仿射变换或者坐标比例尺度改变,可视性仍然保持不变。可视图建网算法能够保持原有时间序列的一些固有特征,即可以将离散时间序列映射成规则网络,进而可以捕捉时间序列的几何结构。 在图1中,顶点的集合可表示为V={v1,v2,v3,v4,v5},边的集合可表示成E={(v1,v2),(v1,v3),(v1,v4),(v1,v5),(v2,v3),(v2,v4),(v3,v4),(v4,v5)}。若采用式(1)定义边的权值,那么图的邻接矩阵为 图的度对角矩阵为 (6) 则GFT的逆变换的定义为 (7) 式中,r为特征值和特征向量的阶次,特征值和阶次一一对应,而阶次与阶次之间是线性关系,特征值与特征值之间是非线性关系,在图谱中通常使用阶次。 GFT可以把一个复杂的图信号分解成一系列不同阶次的特征向量的叠加,它建立了图信号与阶次之间的对应关系。因此,图信号可以通过GFT将其从顶点域变换到图谱域,进而可以实现类似传统频域中“频率”的概念分析[21]。 Shannon[22]首次把熵的概念引入到信息理论中,提出利用信息熵来对事物包含的信息量及反映其状态变化的信息量进行描述。 (8) 根据信息熵理论,本文定义图信号f(n)的图谱幅值熵为 (9) 图谱幅值熵度量了图信号的阶次分布均匀程度,体现了图信号能量分布的图谱域复杂度。当图信号能量集中在少数几个阶次区域时,图谱幅值熵Sf取值较小;当图信号能量在整个阶次区域分布比较均匀时,图谱幅值熵值Sf取值较大。当滚动轴承出现故障,其振动信号必然发生变化,由此转换得到的可视图信号必然不同。不同的故障状态会得到不同的可视图信号,其包含的故障信息也不同,阶次分布的均匀程度亦不同。因此可通过提取可视图信号的图谱幅值熵这一特征指标来指示故障是否发生。 首先将采集的轴承振动信号通过可视图建网方法得到可视图信号;然后通过式(3)计算可视图的邻接矩阵W; 再通过式(4)计算其拉普拉斯矩阵L; 最后通过式(6)和式(9)计算图谱幅值熵Sf,并把该指标作为滚动轴承的特征参数。 马氏距离是由印度统计学家P.C.Mahalanobis提出的,表示数据的协方差距离,它可以有效的计算2个未知样本集的相似度,进而实现对未知样本的预测。马氏距离不受量纲影响,即不受变量之间的相关性干扰。依据实际应用背景,将马氏距离定义为 (10) 对于滚动轴承故障信号,不同类型故障信号的特征参数之间的马氏距离较大,同种类型故障信号的特征参数之间的马氏距离较小。因此,可以将图谱幅值熵作为滚动轴承振动信号的单一特征参数,选择马氏距离作为分类器,从而对滚动轴承故障进行分类。 本文先将采集的滚动轴承振动信号依据可视图建网算法转换成可视图信号,采用式(3)构造邻接矩阵。然后将图谱幅值熵作为滚动轴承特征参数,再通过马氏距离实现故障分类。详细诊断流程如下: 步骤1分别采集滚动轴承正常,滚动体故障,内圈故障,外圈故障振动信号,每种状态进行m次采样,总共有4m个样本。将其分成测试样本和训练样本两组,其中,每种状态训练样本各k个,剩下的4m-4k个样本作为测试样本。 步骤2将每个样本数据转换成可视图,求出每个样本数据图谱幅值熵Sf,并将该指标作为特征参数。 步骤4根据式(10),计算每个测试样本与4种状态训练样本的马氏距离,测试样本与4种训练样本的MD值分别记作d1,d2,d3,d4。 步骤5比较d1,d2,d3,d4,取其中最小的前k个值所对应的训练样本类型为对应的测试样本故障类型,进而判断滚动轴承的状态,达到故障类型识别的目的。 为了验证本文的方法的有效性,采用美国凯斯西储大学电气工程实验室的滚动轴承实测数据[21-22],对滚动轴承不同类型故障进行识别。测试轴承型号为6205-2RS JEM SKF深沟球轴承,采样频率fs=12 000 Hz,轴承转速为1 772 r/min,采样长度N=2 048。人为设置轴承点蚀故障,故障直径为0.177 8 mm,深度为0.279 4 mm,通过加速度传感器分别采集轴承正常,滚动体故障,内圈故障,外圈故障状态的振动信号,4种状态下某一样本振动信号时域波形如图2所示。 图2 不同状态轴承振动信号时域波形Fig.2 Time-domain waveforms of bearings’ vibration signals with different states 每种状态轴承振动信号各截取20个样本,对每种状态取5个样本作为训练样本,其余15个样本作为测试样本,总共有20个训练样本,60个测试样本。根据诊断流程步骤计算各个状态下4个训练样本特征参数的均值和方差。测试样本序列的排列顺序依次为正常状态样本(1~15),滚动体故障样本(16~30),内圈故障样本(31~45),外圈故障样本(46~60)。按照式(10)计算出每一个测试样本与4种状态训练样本的马氏距离,基于可视图图谱幅值熵的马氏距离判别结果如图3所示。 图3中:d1为60个测试样本与正常状态训练样本的马氏距离;d2为60个测试样本与滚动体故障训练样本的马氏距离;d3为60个测试样本与内圈故障训练样本的马氏距离;d4为60个测试样本与外圈故障训练样本的马氏距离。 从图3可以看出,4种测试样本判别结果明显,取马氏距离最小值所对应的训练样本的状态为测试样本的状态类别。由图3(a)可以看出,序列1~15的测试样本d值最小,可以判定序列1~15的测试样本为正常状态样本;由图3(b)可以看出,序列16~30的测试样本d值明显小于其他样本序列,可以判定序列16~30的测试样本为滚动体故障样本;同理,由图3(c)可以判定序列31~45的测试样本为内圈故障样本;由图3(d)可以判定序列46~60的测试样本为外圈故障样本。这判别结果与预期是完全一致的,由此可见,利用可视图图谱幅值熵进行特征提取并用马氏距离判别法判别故障诊断的方法能有效识别滚动轴承故障类型。 图3 4种不同故障类型的马氏距离判别结果Fig.3 Classification results of rolling bearings with four fault types using Mahalanobis distance 上述方法产生的结果都是基于式(3)构造可视图邻接矩阵得到的,为了证明该权值构造邻接矩阵的有效性,分别用式(1)、式(2)构造可视图邻接矩阵,采用同样的分析处理方法对试验一中的试验数据进行分析,得到的结果与基于式(3)构造可视图邻接矩阵得到的结果进行对比,其结果如表1所示。 从表1可以看出,基于W1构造的邻接矩阵方法无法准确地识别各类故障,因为其忽视了各顶点间的差异;基于W2构造的邻接矩阵方法识别率也不高,因为该权值忽视了部分顶点间的差异;而基于平方欧氏距离构造邻接矩阵的方法能够对滚动轴承故障进行准确有效地识别,且对各类故障的正确识别率均为100%。这就表明基于平方欧氏距离构建邻接矩阵的方法优于其他权值构建邻接矩阵的方法,这是因为该权值能如实反映顶点间的差异,进而能捕捉不同故障类型可视图结构的差异,从而对轴承的不同故障类型进行有效准确地识别。 表1 不同邻接矩阵对滚动轴承故障数据识别正确率Tab.1 Fault identification accuracies of rolling bearings using different adjacency matrices % 为了表明本文对滚动轴承故障特征提取方法的优越性,将本文的特征提取方法与基于排列熵(permutation entropy, PE)[23]及多尺度排列熵(multiscale permutation entropy, MPE)[24]的滚动轴承故障特征提取方法对比。在同样的试验条件下,取上述相同的正常状态、滚动体故障、内圈故障和外圈故障4种试验数据进行分析,将其分别编号为1,2,3,4,其中,每种状态训练样本5组,测试样本15组。首先分别利用排列熵、多尺度排列熵和可视图图谱幅值熵提取滚动轴承信号的故障特征;然后根据诊断流程用马氏距离判别函数作为分类器进行故障识别。其中,基于PE的特征提取方法,嵌入维数为m=6,时延为t=2;基于MPE的特征提取方法,嵌入维数为m=6,时延为t=2,尺度因子为s=4。分类结果如图4~图6所示。 对比图4、图5与图6结果可以看出,基于PE以及基于MPE的滚动轴承故障特征提取方法,均出现一定的错误。然而,无论针对上述哪种状态轴承,基于本文可视图图谱幅值熵的特征提取方法均有很好的分类效果,故障识别正确率为100%,表明用GSAEVG对轴承振动信号进行特征提取能够准确的捕捉故障信息,该方法优于基于排列熵以及多尺度排列熵的特征提取方法。 图4 基于PE特征提取的分类结果Fig.4 Classification results based on the feature extraction of PE 图5 基于MPE特征提取的分类结果Fig.5 Classification results based on the feature extraction of MPE 图6 基于GSAEVG特征提取的分类结果Fig.6 Classification results based on the feature extraction of graph spectrum amplitude entropy 为了进一步验证该方法的有效性,将其应用于滚动轴承模拟故障试验台的实测信号。试验台如图7所示,试验轴承型号均为SKF 6206-2RS1/C3,采样频率为8 192 Hz,采样长度为2 048,电动机转速为900 r/min。为模拟轴承故障,使用线切割加工技术分别在深沟球轴承内圈、外圈上切割单点故障,其中内圈故障深度为0.4 mm,外圈设置了2种不同程度故障,深度分别为0.2 mm,0.3 mm。通过加速度传感器分别采集轴承正常,内圈,不同程度外圈故障状态的振动信号,4种状态下某一样本振动信号时域波形如图8所示。 图7 滚动轴承模拟故障试验台Fig.7 Rolling bearing simulation failure test bench 图8 不同故障状态振动信号时域波形Fig.8 Time-domain waveforms of bearings’ vibration signals with different states 采用上述轴承相同的故障诊断方法。先将训练样本进行训练,计算出训练样本特征参数及方差;然后根据式(10)计算出每一个测试样本与每一类训练样本的d值;最后根据d值对测试样本进行分类。在图9中,测试样本序列的排列顺序依次为正常状态(1~15),内圈故障(16~30),外圈故障1(31~45),外圈故障2(46~60)。图9中:d1为60个样本与正常状态训练样本的d值;d2为60个测试样本与内圈故障训练样本的d值;d3为60个测试样本与外圈故障1训练样本的d值;d4为60个测试样本与外圈故障2训练样本的d值。同理可知,马氏距离最小值所对应的训练样本的状态为测试样本的状态类别,从图9可以看出,每类故障都能有效的进行识别。 图9 不同故障类型的马氏距离判别结果Fig.9 Classification results of rolling bearings with different fault types using Mahalanobis distance 为了进一步体现本文方法的优越性,在此次试验基础上,同样地将本文的特征提取方法与基于PE及MPE的滚动轴承故障特征提取方法对比。其中,基于PE与MPE方法的参数与试验一中的参数相同。取上述相同的4种试验数据(正常、内圈故障、外圈故障1、外圈故障2)进行分析,将其分别编号为1,2,3,4,其中,每种状态训练样本5组,测试样本15组。首先分别利用PE,MPE和GSAEVG提取滚动轴承信号的故障特征;然后根据诊断流程用马氏距离判别函数作为分类器进行故障识别。分类结果如表2所示。 表2 基于不同方法特征提取的分类结果Tab.2 Classification results based on feature extraction from different methods 由表2可以看出,基于PE以及基于MPE的滚动轴承故障特征提取方法,均出现一定的错误。然而,无论针对上述哪种状态轴承,基于本文GSAEVG的特征提取方法均有很好的分类效果,故障识别错误数为0,进一步表明用图谱幅值熵对轴承振动信号进行特征提取能够准确的捕捉故障信息,其特征提取效果优于传统的基于排列熵以及多尺度排列熵的特征提取方法。 针对轴承故障特征难以提取的问题,本文将复杂网络与图信号处理引入机械故障诊断领域,提出了基于可视图图谱幅值熵和马氏距离的滚动轴承故障诊断方法。主要结论如下: (1) 将轴承振动信号转换为可视图信号,通过GFT将可视图信号从顶点域变换到图谱域,进而在图谱域对轴承振动信号进行特征提取,从而为故障诊断的特征提取方法提供了一条不同于传统的时域、频域或时频域分析的新途径。 (2) 可视图图谱幅值熵度量了可视图信号的阶次分布的均匀程度,体现了可视图信号能量分布的图域复杂度,不同故障类型可视图信号能量分布图域复杂度不同。通过可视图图谱幅值熵能有效地提取出轴承的不同故障特征。应用实例分析结果表明,与传统的排列熵及多尺度排列熵特征提取方法比较,本文方法能够更有效准确地提取滚动轴承故障特征。 (3) 需要说明的是,本文是在有监督分类基础上进行滚动轴承故障诊断,接下来笔者将研究低标签及无标签下的机械故障诊断,即在已知部分故障样本标签或无故障样本标签基础上进行机械故障诊断。

2 图谱幅值熵
2.1 图傅里叶变换

2.2 图谱幅值熵


3 滚动轴承故障特征提取和分类
3.1 特征提取
3.2 马氏距离分类
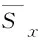
4 故障诊断流程
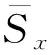
5 应用实例
5.1 试验一





5.2 试验二




6 结 论

