极化码编码理论综述

李莉萍，侯妍妍

(安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039)

0 引言

当前，第五代移动通信(5G)正在被学术界、工业界积极研究，很多国家及地区亦在进行5G服务的部署；与此同时，世界范围内也开始了对第六代移动通信(6G)的新理论、新技术的调查研究[1-2]。在5G通信中，目前已确定使用极化码(polar code)[3]作为增强移动宽带场景(eMBB)控制信道编码方案[4-5]。

本文先对极化码的编码原理进行简单介绍，然后重点描述极化码编码构造方案的研究进展，并对各个构造方案进行介绍，以展示极化码的编码构造理论与技术的全面图景。

1 极化码基本原理

文献[3]给出了极化码的基本理论，本节介绍文献[3]中的相关内容，以引出极化码的编码构造问题。

对于任意码长N(N=2n，n≥0)，极化码的编码可以表示为：

xN1=uN1GN，

(1)

对于任意一个B-DMC信道W:x→y，其中x表示输入字符集，y表示输出字符集，则信道转移概率可以表示为W(y|x),x∈x={0,1},y∈y。极化码编码后的码字xN1在N个底层信道W上进行传输，得到输出信号yN1，这个过程产生向量信道WN，其转移概率为：

(2)

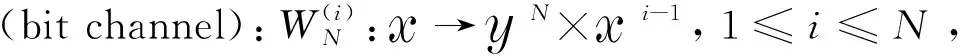
(3)

在文献[3]中已证明，当N趋于无穷大时，这N个比特信道，一部分是完美的无噪声信道，另一部分是纯噪声信道，且无噪声信道所占的比率是底层信道W的信道容量。这个现象就是信道极化的现象，也是极化码名称的由来。

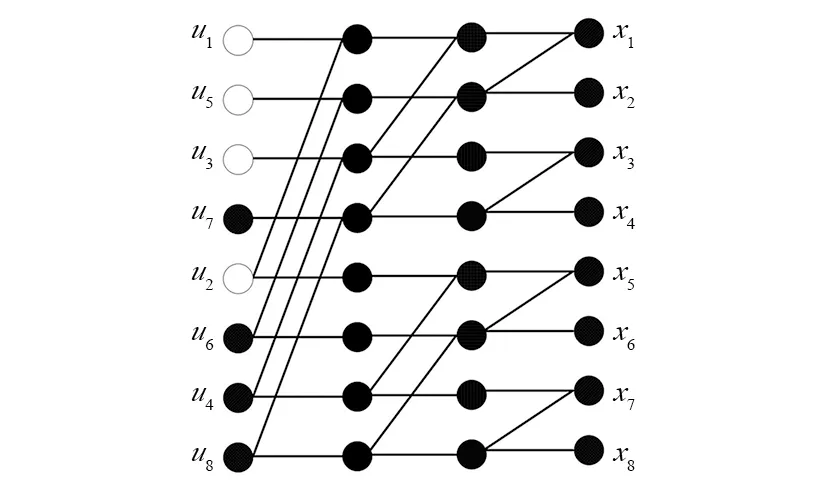
图1 极化码编码示意图(N=8，信息位集合：A={4,6,7,8}，左侧白色节点表示固定位信息)Fig.1 An encoding example of polar codes

实际码长N是有限的，中短码长的极化码，信道不会充分极化，比特信道中有些信道，其信道质量在无噪声信道与纯噪声信道之间。极化码的构造问题，就是对于给定的底层信道W、码长N、码率R，如何确定哪些比特信道质量相对较好，也就是要确定信息比特信道集合A，在这些信道上传输信息位比特。下面将对极化码的构造问题进行阐述，详细介绍目前的构造算法。

2 极化码构造问题

如上所述，极化码的构造，其实质是确定传输信息位比特的比特信道集合A，这些信道相对于固定位比特信道，应具备更好的信道质量。除了比特信道容量，也可以通过巴氏参数(Bhattacharyya parameter)来衡量比特信道质量。巴氏参数是最大似然估计下，传输一次时的错误估计概率上限，因此，巴氏参数值越小，错误估计上限越小。极化码第i个比特信道的巴氏参数定义为：

(4)

文献[3]中，作者给出了二进制删除信道(Binary Erasure Channel, BEC)的信道容量及巴氏参数的递推公式，依据递推公式，可以确定地算出每个比特信道的信道容量或者巴氏参数，进而可以选择信道容量大(巴氏参数小)的比特信道作为传输信息位的信道，这些信道构成了集合A。因此，对于BEC信道，极化码具有确定的构造方法；而对于其他类型的B-DMC信道，没有确定的公式来进行构造。

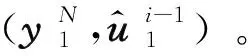
3 编码构造方案

3.1蒙特卡洛方法构造

极化码的构造，可以通过计算各个比特信道的巴氏参数，上文提到，由于输出符号个数巨大而无法精确计算。文献[3]提出可以使用近似的方法来计算巴氏参数，其中一种方法就是使用蒙特卡洛(Monte Carlo)方法来进行巴氏参数的估计。作者证明了巴氏参数是如下随机变量的期望：

而此随机变量，就是文献[3]中提出的复杂度为O(NlogN)的串行抵消译码算法(Successive Cancellation, SC)计算的判决值。因此，用一个SC译码器，可以用蒙特卡洛仿真的方式，预测出各比特信道的巴氏参数，进而进行极化码的构造。

3.2 密度进化构造及高斯近似构造

极化码的编码与解码图，可以等效转换为因子图(factor graph)[3]。极化码的密度进化(Density Evolution, DE)构造[6-7]方法使用低密度奇偶校验码(Low Density Parity Check, LDPC)中的密度进化方法，对极化码因子图中的节点，递归计算其对数似然比(Log Likelihood Ratio, LLR)的密度函数。在获得每个根节点(对应于相应的比特信道)密度函数后，可计算出每个比特信道对应的错误概率。那么，极化码的构造可以通过选择错误概率之和最小的K=NR个比特信道作为信息位集合A。

在递归计算密度函数过程中，需要计算密度函数的卷积。在卷积运算中，需要合理选择精度以避免量化误差对结果的影响。在文献[8-9]中，针对加性高斯白噪声信道(Additive Gaussian Noise Channel，AWGN),作者提出使用高斯近似的方法来降低密度函数的计算复杂度。假设传输全零信息位，那么信道接收到的信号以及递归计算过程中的中间节点的LLR，都服从高斯分布，且高斯分布的方差是均值的2倍。所以，在计算过程中，只需要递归计算LLR的均值即可。递归计算的过程中，基本计算单元如图2所示。

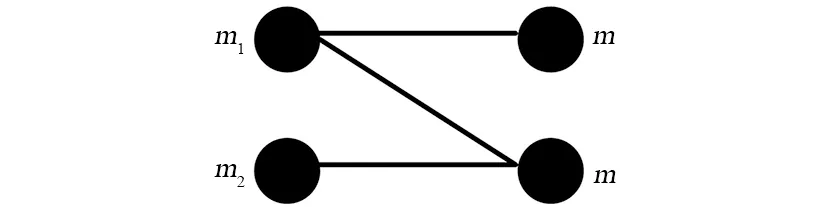
图2 LLR递归计算基本单元Fig.2 Basic unit of LLR calculation

假设一个高斯分布的LLR的均值为m, 则此高斯分布是N(m,2m)。在递归计算中，用高斯近似可以计算出下一级两个LLR的均值，分别为：

m1=f1(m),m2=f2(m)；

其中，f1(x)和f2(x)分别为：

(5)

(6)

(7)

通过上述方法，在极化码的因子图中进行LLR的递归计算，即可求出最终每个比特信道的误码率。极化码的构造，可以通过选择误码率之和最小的K个信道作为信息位集合。最后需要说明的是，文献[11]中发现，式(7)中的两段近似方案，不能满足码长稍大时的精度要求。比如，在码长N≥214时，两段的高斯近似方法构造结果误差较大。因此，在文献[11]中，提出了改进的近似函数，使得极化码高斯近似的构造，在码长为N=218时，仍能提供高精度的构造结果。

3.3 Tal-Vardy构造

在第2节的讨论中，可以看出极化码构造的难点在于每个比特信道的输出符号个数太多，无法精确计算比特信道的信道容量或者巴氏参数。在文献[12]中，作者合并每级比特信道输出符号的个数，使得最终的比特信道符号是一个固定的值，这样一来，输出符号个数不随码长增大而增大，进而可以方便计算比特信道的错误概率。文献[12]的作者是Tal和Vardy，因此这个构造被称为Tal-Vardy构造。

码长N=8时，极化码每一级比特信道的演进情况如图3所示。从最右侧的底层信道W起始，每一级信道的输出符号个数，至少都是前一级输出符号个数的平方。在文献[12]中，作者提出两种方案，每种方案的核心都是限制每个级别比特信道的符号个数，比如限制最终的输出符号个数为μ。限制的方式是通过合并输出符号，直到输出符号的个数是μ为止。以其中一种方案为例，此方案在每次合并输出符号时，具有一定的质量损失，而每次合并的准则是使得合并前后互信息损失最小。

图3 每一级比特信道演进(N=8)Fig.3 Bit channel transformation in each level(N=8)

在Tal-Vardy构造中，因每一级输出符号个数为μ，最终的比特信道输出符号个数也是μ，比如μ=256。对于输出符号一定的比特信道，可以直接算出错误概率，选择错误概率之和最小的K个比特信道构成信息位集合。Tal-Vardy构造复杂度可控，给定输出符号个数μ，其复杂度为O(Nμ2log2μ)，且适合任何B-DMC信道。对Tal-Vardy算法，文献[13]进行了推广，对原始的N个相同的底层信道W，推广为N个任意的底层B-DMC信道(可以不同)，使得Tal-Vardy算法能支持极化码在广义底层信道条件的构造。

3.4 部分序构造

部分序(Partial Order, PO)在文献[7,14]中被提出，在文献[15-16]中使用部分序进行了极化码的具体构造。

3.5 极化重量构造

极化重量(Polarization Weight, PW)在文献[17-19]被提出。对于比特信道i，对应的极化重量定义为：

(8)

式(8)在数学上称为β展开，其中β为一个常数。在文献[17]中，β的值根据经验选择为21/4。对每个比特信道都可以算出其对应的极化重量，极化重量越大，表示信道质量越好，最终可以选择极化重量最大的K个信道作为传输信息位的比特信道。

用极化重量的方法进行信道排序，在计算信道质量时，与底层信道类型无关，可以事先算出给定码长N的所有比特信道质量。并且，极化重量还具有对称性及嵌套性(nesting)[18]。极化重量的嵌套性，可以用来支持在给定最大码长N的情况下，任意码长N'≤N与任意码率R的组合。以此为基础，在5G标准中文献[5]给出的信道序列，是码长最大为1 024时，比特信道按照质量从差到好的排序列表：对任意码长与码率，只需从列表中从前到后选择出固定位的比特信道即可。

利用极化重量对极化码的构造，计算复杂度低且对任意信道适用，对任意码长码率的支持灵活，因而在5G标准中得到了应用。需要指出的是，对于具体的某一个底层信道、码长和码率，极化重量的构造方法不一定会产生最优的排序结果。在实际系统设计时，需根据具体场景进行合适的选择。

3.6 极化谱构造

极化谱(polarization spectrum)在文献[20]中被提出，是近期极化码构造方面的新进展。在文献[20]中，对第i个极化信道，定义一个子码，其生成矩阵是原始生成矩阵第i行至最后一行对应的矩阵，那么第i个信道对应的极化子码(polar subcode)，则是编码序列的第i位是1时，通过子码编码矩阵编码后对应的所有码字。极化谱是极化子码的重量分布。第i个比特信道的巴氏参数联合界(Union Bhattacharyya Bound, UB)，与极化谱分布相关，也与底层信道巴氏参数相关，具体如下所示：

(9)

重量谱的计算通常比较复杂且没有闭合公式，在文献[20]的工作中，通过对极化子码的对偶码的研究，运用MacWilliams 等式，作者提出了计算极化谱的递归算法，总体复杂度为O(N3)。构造结果表明，在SC译码下，极化谱构造方法略差于GA及Tal-Vardy构造算法，但是在SC的列表译码(SC List Decoding, SCL)时[21-22]，优于GA、Tal-Vardy和PW构造方法。

3.7 人工智能构造

如以上讨论，极化码构造计算复杂且没有一个统一的公式。并且，前文所述的构造方法(除了极化谱)，理论上都是基于SC译码进行的优化，而现有的SCL译码以及BP译码(Belief Propagation)，没有针对性的优化构造。此类问题比较适合人工智能方法的应用，典型工作参见文献[23-24]。

在文献[23-24]中，针对极化码的构造，作者提出使用遗传学习(genetic learning)的方法进行构造。构造过程中，不提供极化码构造的已知方法，比如前文提到的巴氏参数、高斯近似及Tal-Vardy构造等。遗传学习构造的极化码，通过现有的SC或者SCL译码器进行译码，译码的错误概率作为遗传学习算法下次构造的输入，这个循环一直进行，直到构造出符合性能指标的极化码(或者最大构造次数到达)。通过遗传学习算法构造的极化码，在SCL及BP译码下，比现有的构造方式具有更好的性能。在文献[24]中，还对嵌套的极化码构造进行了优化，以对任意码长码率的极化码进行支持。人工智能的构造，计算量比较大，可以采用线下构造好之后再使用的方式。

4 结束语

本文指出了极化码编码构造的难题，进而引出极化码构造方面的主要构造方法，除了BEC信道的确定构造方案，主要介绍了蒙特卡洛构造、密度进化构造、高斯近似构造、Tal-Vardy构造、部分序构造、极化重量构造、极化谱构造以及基于人工智能的构造。极化码构造理论仍然有未知的领域，比如，除了目前已知的两个部分序，是否还存在其他类型的部分序？除了SC译码，其他译码方式下(比如SCL和BP译码)的极化码构造，理论上的支持仍然未知，目前只能通过极化谱构造或者人工智能的方式进行搜索。极化码的构造理论与技术实现，需要更多的突破。