基于联合译码的RS码中继协作系统设计

高 璇，仰枫帆，毛 健

(南京航空航天大学，江苏 南京 210016)

0 引言

编码协作是由Hunter等提出的将信道编码和协作通信技术相联合的技术，协作用户将码字的不同部分分别通过相互独立的信道发送至目的节点，可以同时获得编码增益和协作分集增益[1]。在之前的研究中，许多作者针对不同的信道编码在协作通信系统下的性能表现进行了研究，其中包含Turbo码[2]、LDPC码[3]、Polar码[4]等，但对基于RS码的中继协作系统的性能的研究却非常少。

里德-所罗门(Reed Solomon, RS)码[5-6]是一种纠错能力很强的循环码，被广泛用于数字通信系统和存储系统中。RS采用多进制编码，能够有效纠正突发错误，并且其译码复杂度也低。现如今基于RS码的协作通信系统大多采用在中继节点截短信息位以生成一个冗余位较多的RS码方式来提高编码增益[7]，而这种方式受限于RS码的码长固定性，并不能够很好地适用于码率自适应的运用场景。在实际应用中，为满足不同系统的具体要求，一般需要选用码长较为灵活的码以适应不同的应用场景。因此，本文提出了一种新的基于联合译码的缩短RS码中继协作系统，该方案在源节点设置了码长自由的缩短RS码，在中继节点设置了冗余位较多的RS码，并在目的节点设计了两种联合译码方案。通过实验仿真证明了该方案具有良好的性能增益,并且能够根据不同的系统要求配置不同的码率。

1 缩短RS码的构造

令α为伽罗华域GF(2m)的本原元，则符号取自GF(2m)，码长为n=2m-1的RS码，其生成多项式是以α,α2,α3,…,α2t连续根为其全部的根，具体形式如下：

g(x)=(x-α)(x-α2)...(x-α2t)，

(1)

式中，t为RS码的最大纠错码元数，n-k= 2t为校验位数。RS码的最小距离为2t+ 1，则RS码的最小距离比校验位数大1。因此，RS码是极大距离可分码(Maximum Distance Separable, MDS)。

2 缩短RS码中继协作系统的构造

一般地，中继协作通信系统包含3个节点：源节点S、中继节点R和目的节点D。源节点通过广播的方式向中继节点和目的点发送消息，中继节点对接收到的消息进行处理后再发送至目的节点，目的点对两路消息进行联合处理后得到所需的结果。编码协作通信的设计涉及到两个关键问题：如何设计编码方法与如何设计联合译码方案[11]。为解决这两个关键问题，设计了如图1所示的基于SRS码的中继编码协作系统方案。

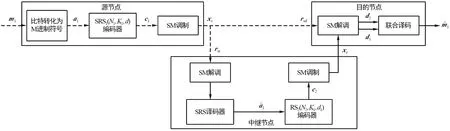
图1 缩短RS码中继编码协作系统的模型Fig.1 Model of RS coded-cooperation system scheme based on shortened RS

2.1 中继协作编码方案的设计

中继编码协作系统中源节点生成的序列需要两个时隙用于传输。第一时隙源节点直接发送生成的序列；第二时隙中继节点通过重新编码的方式发送校验位更多的序列以提高编码增益。下面将对源节点和中继节点的编码过程进行说明。

2.1.1 源节点编码方案的设计

在时隙1期间，源节点的编码过程可分为如下步骤：

① 源节点随机生成长度为K× log2(M)的二进制序列m1并将二进制序列m1映射到非二进制M元符号序列a1，其中M是调制阶数，序列a1中元素均来自GF(2m)。

② 对信息符号序列a1进行RS1(N,K,d)系统编码，其中N是RS1码的码长，K是信息序列的长度，d是RS1码的最小距离且d=N-K+ 1。RS1的生成多项式以N-K个连续根构成其全部根，可表示为下式：

g1(x)=(x-α)(x-α2)...(x-αN-K) ，

(2)

式中，αj1∈GF(2m), 0 ≤j1≤N-K。使用RS1(N,K,d)系统编码，可以得到RS1码的系统码多项式：

c(x)=a(x)+b(x)xK，

(3)

其中，b(x)=b0+b1x+b2x2+...+bN-K-1xN-K-1,bi∈GF(2m)为校验多项式，由GF(2m)上的多项式除法计算得到：

b(x)=xN-Ka(x)/g1(x)，

(4)

rsr=hsrxs+nsr，

rsd=hsdxs+nsd，

(5)

其中，h是瑞利衰落信道向量，其每个元素为均值为0和方差为1的复高斯随机变量。n是复AWGN向量，其每个元素为一个均值为0和方差为σ2/2的复高斯随机变量。

2.1.2 中继节点编码方案的设计

在时隙2期间，中继节点接收到从源节点来的接收序列rrd，对序列进行处理并转发给目的节点。其具体过程可分为如下步骤：

g2(x)=(x-α)(x-α2)...(x-αN2-K1)，

(6)

其中，αj2∈ GF(2m), 0 ≤j2≤N2-K1。使用RS2(N2,K1,d1)系统编码，可以得到RS2码的系统码多项式

(7)

其中，b2(x)为校验多项式，由GF(2m)上的多项式除法计算得到：

(8)

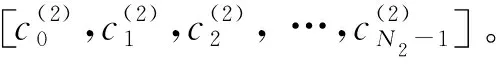
rrd=hrdxr+nrd。

(9)

2.2 协作系统目的点联合迭代译码算法的设计

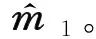
2.2.1 基于阈值选择的目的点联合迭代译码算法

图2 基于阈值选择的并行译码方案Fig.2 Parallel decoding scheme based on threshold selection

(10)

2.2.2 基于MRC技术的目的点联合迭代译码算法

当使用上述的基于阈值选择的并行译码算法时，需要根据实际信噪比的大小决定选取一路输出作为估计序列，为了充分利用协作系统下两路信号，进一步降低误码率，提高可靠性，提出了基于MRC技术的串行译码算法。如图3所示，基于MRC技术的串行译码方案是首先利用MRC技术对两路信号进行合并处理成一路信号,即得到一个合并信息符号序列，再附加上第二路的校验符号，使其能够组合成长度为N2的序列，再对序列进行解调及译码。

图3 基于MRC技术的串行译码方案Fig.3 Serial decoding scheme based on MRC technology

基于MRC技术的目的点联合迭代译码算法的实现步骤如下：

① 首先，将接收序列rsd和rrd分割成两部分，前一部分对应的是信息符号经过两路传输后得到的接收符号rsd,1和rrd,1，后一部分对应的是校验符号两路经传输后得到的接受符号rsd,2和rrd,2。

② 对rsd,1和rrd,1进行MRC合并成rMRC，合并系数参考MRC合并方式，合并结果为：

rMRC=φrsd,1+(1-φ)rrd,1，

(11)

其中，合并系数φ与源节点至目的节点的信道信噪比SNRsd和中继节点和目的节点的信道信噪比SNRrd有关，具体表示形式如下：

(12)

③ 将rrd,2附加到rMRC后，可以得到一个长度为N2的序列rc=[rMRC,rrd,2]。

3 仿真结果与性能分析

根据本文构造的基于SRS码的中继编码协作系统，对其在AWGN信道和衰落信道下进行仿真和分析。设α为本原多项式p(x)=x6+x+1的根，假设本次仿真在源节点选取SRS码的原码为符号取自GF(26)的RS1(61, 51, 13)，其生成多项式以α,α2,α3,…,α12为其全部根，可表示为：

g1(x)=(x-α)(x-α2)(x-α3)...(x-α12)。

(13)

在中继节点选取符号取自GF(26)的RS2(63, 31, 33)，其生成多项式以α,α2,α3,…,α32为其全部根，可表示为：

g2(x)=(x-α)(x-α2)(x-α3)...(x-α32)。

(14)

令源节点到目的节点的信道信噪比表示为γsd，中继节点到目的节点的信道信噪比表示为γrd，令源节点到中继节点的信道信噪比表示为γsr。因为中继节点距离目的节点比源节点距离目的节点近，中继节点具有信噪比优势，即γrd=γsd+1。在仿真中，根据中继节点是否译码正确可分为理想状态与非理想状态。在理想状态中，可以假设从源节点到中继节点之间的信噪比γsr为无穷大，而在非理想状态，需根据具体情况设置源节点到中继节点之间的信噪比。

3.1 RS码、LDPC码和Turbo码比较

如表1所示，对RS码、Turbo码和LDPC码从其性能、编码复杂度和译码复杂度等方面做比较研究，利于进一步对比他们的优缺点。

表1 RS码、Turbo 码、LDPC码三者对比Tab.1 Comparison of RS code, Turbo code and LDPC code

其中，m为Turbo码卷积编码器的记忆长度，Imax为最大迭代次数，N为码长，P=N-K为校验比特长度，dυ和dc分别表示LDPC码的校验矩阵中的列重和行重。

RS码是极大距离可分码，编译码复杂度低，适用于工程实现。Turbo 码的MAP译码算法能充分利用软判决，有较好的纠错性能，但其利用迭代译码，译码复杂度较高。LDPC 码在长码情况下性能较佳，但通过矩阵乘法进行编码十分复杂，BP 译码算法也需要大量迭代，产生了较高的复杂度。

3.2 缩短RS码的缩短长度对码性能的影响

由上文可知，本文设计的中继编码协作源节点选取系统缩短RS码，而选取的缩短RS码并未固定，因此下面讨论缩短RS码的缩短长度的码的性能的影响，以确定合适的缩短的长度。在仿真中，设置传输1 000 000帧数据，选取4个缩短长度不同的缩短RS码(SRS(53, 41)，SRS(43, 31)，SRS(33, 21)，SRS(13, 1)，并且均采用64-QAM调制方式和Euclidean译码算法，AWGN信道下不同缩短长度的缩短RS码的性能仿真结果如图4所示。

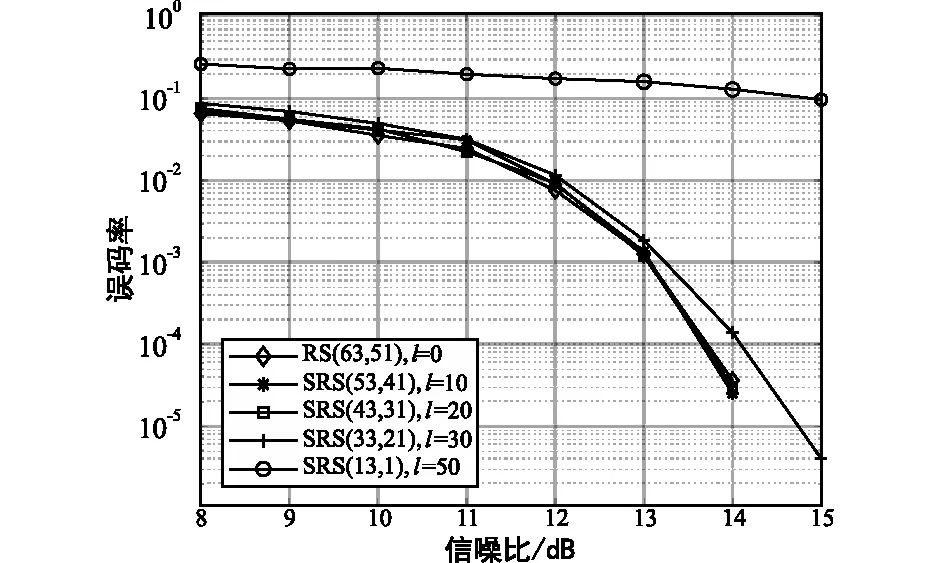
图4 AWGN信道下不同缩短长度的缩短RS码的性能比较Fig.4 BER performance of shortened RS codes with different shortened lengths over Gaussian channel

从理论上分析可得，在校验位长度一样时，随着缩短长度l的增大，缩短RS码的纠错能力保持不变，编码速率逐渐减小，译码复杂度降低。由图4可知，在非极限情况下，缩短长度l的变化对误码性能的影响较小，即码率降低对缩短RS码整体误码性能的影响较小。但在极限情况下，当删除位数过多时，码率迅速减小，误码性能迅速变差，实际应用价值不大。因此通过综合考虑误码性能和编码码率实用性及编译码复杂度，我们需要选取一个合适的缩短长度，在本次仿真选取缩短长度为20的SRS(43, 31)。

3.3 AWGN信道下两种联合迭代译码算法的性能对比

在AWGN信道下对中继编码协作系统进行仿真，首先通过预仿真获取输入信道比阈值,如图5所示。

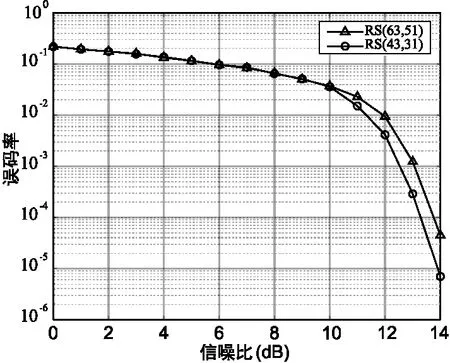
图5 AWGN信道下的预仿真Fig.5 Pre-simulation diagram over Gaussian channel

通过预仿真，可以得到输入信道比阈值为δ1=10 dB。在AWGN信道下将非协作和编码协作系统的性能进行比较，如图6所示。从图6中可以看出，在输入信噪比较高的情况下，本文设计的中继编码协作系统较非编码协作系统性能更优。在理想状态下，当误码率为10-4时，利用基于MRC技术的联合译码方案的协作系统较利用基于阈值选择的联合译码方案的协作系统约有1.3 dB的性能提升，编码协作系统较非协作系统有3.3 dB的性能提升。此外，非理想状态(γsr=1)下和理想状态(γsr=)下的性能相当，在信噪比为10-4的时候，对于采用基于MRC技术的联合译码方案的协作系统，理想状态下的性能较非理想状态下有0.3 dB的提升，这说明了RS码是一个纠错能力强的码。

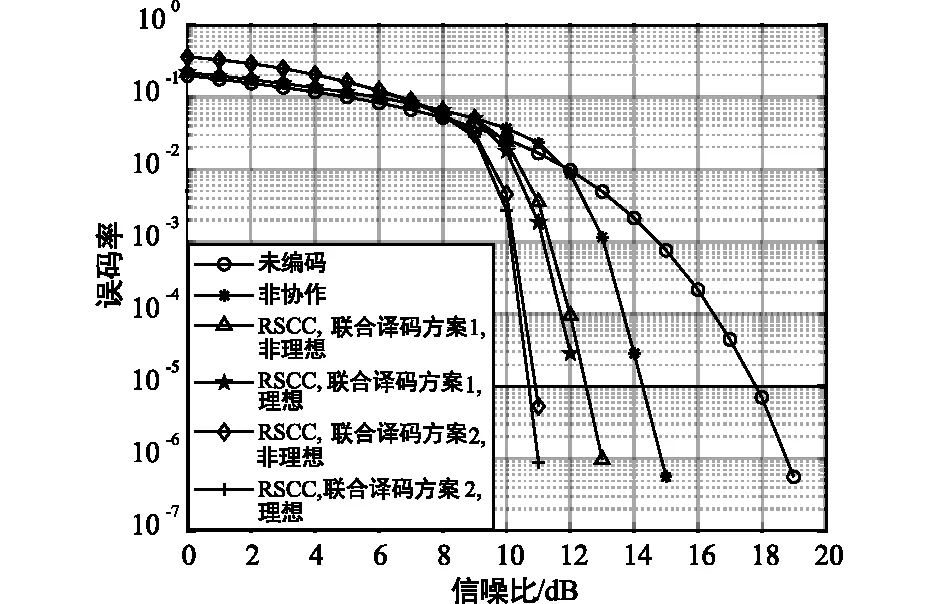
图6 AWGN信道下编码协作系统性能比较Fig.6 BER performance of RS coded-cooperation system over Gaussian channel

3.4 瑞利衰落信道下两种联合迭代译码算法的性能对比

在瑞利快衰落信道下对中继编码协作系统进行仿真，首先通过预仿真获取输入信道比阈值，如图7所示。

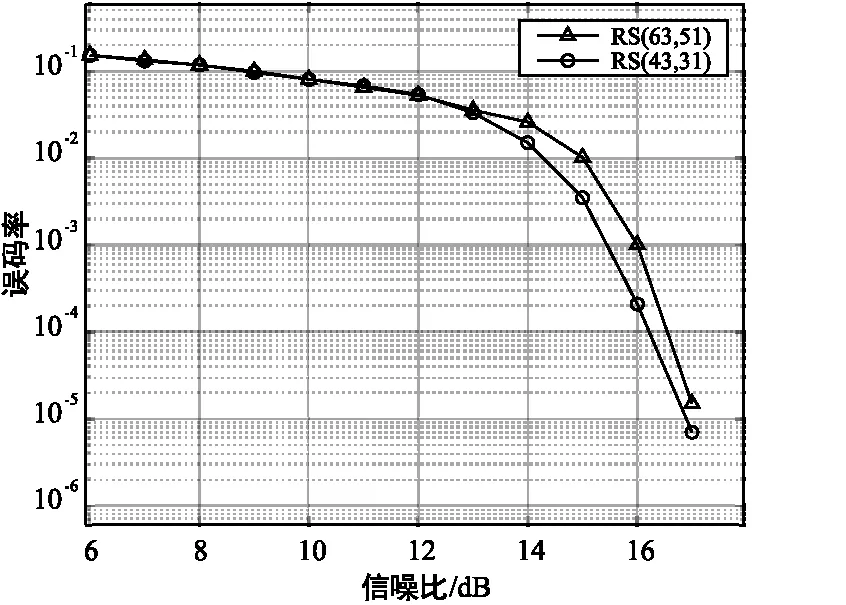
图7 瑞利快衰落信道下的预仿真Fig.7 Pre-simulation diagram over Rayleigh Fading channel

通过预仿真，可以得到在瑞利快衰落信道下输入信道比阈值为δ2=13 dB。在瑞利快衰落信道将非协作和编码协作系统的性能进行比较,如图8所示。从图8中可以看出，在理想状态下，当误码率为10-4时，利用基于MRC技术的联合译码方案的协作系统较利用基于阈值选择的联合译码方案的协作系统有1.8 dB的性能提升，编码协作系统较非协作系统有4.7 dB的性能提升。同样可得，在输入信噪比较高的情况下，本文设计的中继编码协作系统较非编码协作系统性能更优。

图8 瑞利快衰落信道下编码协作系统性能比较Fig.8 BER performance of RS coded-cooperation system over Rayleigh Fading channel

4 结束语

本文在对RS码和协作通信技术的研究基础上，设计了基于SRS码的中继编码协作系统方案。此方案在源节点设置SRS码，中继节点设置校验位更多的RS码，既实现了码率灵活，又提高了系统纠错能力。为对从源节点和中继节点传输来的接收序列进行译码，本文提出了基于阈值选择的联合译码方案和基于MRC技术的联合译码方案两种译码方案。通过在AWGN信道和瑞利快衰落信道下对中继编码协作系统进行仿真实现，仿真结果表明，编码协作系统较非协作系统性能更优，并且利用基于MRC技术的联合译码方案较利用基于阈值选择的联合译码方案，对中继编码协作系统性能提升更为明显。