LDPC-CRC-极化码级联码及其比特翻转译码算法

尹 超，潘志文,2，刘 楠，尤肖虎,2

(1. 东南大学 移动通信国家重点实验室， 江苏 南京 210096；2. 网络通信与安全紫金山实验室， 江苏 南京 211100)

0 引言

极化码[1]是唯一一种被理论证明在二进制输入无记忆对称信道(Binary Input Discrete Memoryless Symmetric Channel, BI-DMSC)下达到香农界的编码方式[2]。然而，有限码长下，极化码在串行抵消(Successive Cancellation, SC)译码算法下的误码率性能不如低密度奇偶校验(Low-Density Parity Check, LDPC)码[3]和Turbo码[4]。

串行抵消列表[5](Succesive Cancellation List, SCL)译码器和串行抵消翻转[6](Succesive Cancellation Flip, SCF)译码器都是在SC译码器基础上的改进，它们都表现出极好的误块率(Block Error Rate, BLER)性能。与循环冗余校验(Cyclic Redundancy Check, CRC)码级联后，极化码的译码性能超越了LDPC码。由于SCL算法有很长的译码时延[7]，置信传播(Belief Propagation, BP)译码算法因其并行计算的特征受到人们广泛关注[8-10]。文献[9]提出了置信传播列表(Belief Propagation List, BPL)译码算法，选择多个基于不同因子图BP译码器并行译码。置信传播比特翻转算法[10](Belief Propagation Bit-flip, BPF)借用关键集合(Critical Set)的概念标记易错比特，在BP译码算法中引入比特翻转的操作，提升了BLER性能。

除了对译码算法进行改进，也有一些针对极化码的编码做出的尝试[11-13]。文献[11]首先提出通过利用LDPC码作为外码保护极化码中间信道(Intermediate Channel, IC)中传输的比特以获得更好的BLER性能。

本文提出了一个改进的LDPC-极化码比特翻转译码算法，通过每次对关键集合内的比特进行比特翻转，在给定的翻转次数下，性能较LDPC-极化码的置信传播译码算法有了极大的提升。通过构造LDPC-CRC-极化码的三级级联码，在比特翻转译码算法下的BLER性能得到了进一步的提升。

1 预备知识

1.1 极化码与置信传播译码算法

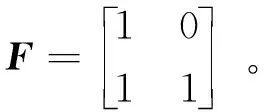
BP译码算法依赖于极化码编码所形成的因子图。对于码长N=2n的极化码，它的因子图是由n+1阶段的N×(n+1)个节点组成。当N=8时，极化码的BP因子图如图1所示。因子图中每个阶段包含N/2个如图2所示的基本处理单元(Processing Element, PE)进行信息计算，每个节点将其对数似然比(Log Likelihood Rate, LLR)信息存储在N×(n+1)的矩阵L,R中。BP迭代译码的过程就是迭代的矩阵L和R之间传递信息的过程。

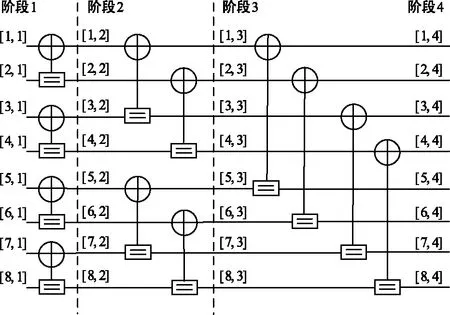
图1 码长为8的极化码BP因子图Fig.1 Factor graph of polar codes with length N=8

图2 BP因子图中的PE示意图Fig.2 PE in factor graph of polar codes

1.2 LDPC-极化码级联码

由于极化码的信道极化现象，比特信道ui,i∈{1,2,...,n}或者变成完全无噪声(称其为“好信道”)，要么变得完全噪声(称其为“坏信道”)。比特信道ui的质量由对应的巴氏参数(Bhattacharyya parameter)Z(ui)度量。Z值越低，对应的比特信道错误概率越低，这些信道就是好信道，用来传输信息比特。另一方面，Z值越高，对应的比特信道错误概率越高，这些信道就是坏信道，用来传输冻结比特。然而，由于有限码长极化码极化现象不充分，导致有一部分比特信道既不是完全无噪声，又不是完全噪声，(称其为“中间信道”)。对于一个信息集合为A 的中间信道，中间信道对应信息集合中那些有相对较大Z值的比特信道。文献[11]提出使用短的LDPC码作为外码，对极化码的中间信道提供额外保护，内码使用极化码，以此构成了LDPC-极化码级联码。当N=8时，LDPC-极化码的BP联合因子图如图3所示。

图3 级联极化码的联合因子图Fig.3 Joint factor graph of concatenated polar codes

LDPC-极化码根据联合因子图进行置信传播译码。联合因子图内部是一个基于极化码生成矩阵的极化码因子图，在信息传输到阶段1时，将阶段1计算得到的信息传入LDPC的变量节点(Variable Node, VN)。随后根据LDPC因子图进行迭代次数为1的BP译码，变量节点将计算得到的信息再次传入极化码的因子图。当信息传输到阶段4时，一次联合因子图的BP译码就结束了。当BP迭代次数达到设定好的最大迭代次数时，根据对信息集合A中比特信道的LLR做比特判决，得到信息比特ui,i∈{1,2,...,n}估计值。

1.3 关键集合与比特翻转算法

极化码的结构可以表示为一颗二叉树，其叶节点指向极化码的信息比特和冻结比特的集合。在二叉树表示法中，叶节点全是信息比特的节点被称为Rate-1节点[14]。Rate-1节点中第一个比特的索引构成了关键集合[15](Critical Sets, CS)。例如，对于极化码P(32,16)，码构造算法使用高斯近似算法(Gaussian Approximation, GA)，信道信噪比Eb/N0=2.5 dB时，CS={12,14,15,20,22,23,25}。CS中的信息比特被证明是不可靠的。

比特翻转首先被用于SC译码算法，随后文献[10]将其引用至BP译码算法中。文献[10]用BPF-ω表示一个单次最大翻转比特数为ω的BPF译码过程，T表示构造的关键集合CS-ω中元素的个数(也是比特翻转的最大次数)。当ω=1时，CS-1退化为Rate-1节点中第一个比特的索引构成的关键集合CS。在BPF-ω算法中，对于一个待翻转比特，它的先验LLR被指定为+或者-，分别对应猜测此信息比特为0或者1。因此，BPF-ω共包括多达2ω×T次额外的BP译码尝试。BPF极大地提高了极化码BP译码算法的BLER性能，但是，相比于中等列表长度的CA-SCL译码器，BPF算法的译码性能仍有差距。同时，它的译码时延也比BP算法高了很多。

2 改进的LDPC-极化码比特翻转译码算法

尽管基于BP译码算法的LDPC-极化码BLER性能相比极化码在中高信噪比处有0.3 dB左右的提升，但是其BLER性能仍不足以用于现实的数据传输。在这部分，提出一种改进的LDPC-极化码比特翻转译码算法，在对联合因子图进行BP译码失败后，通过对CS中信息比特的翻转，LDPC-极化码获得很大的性能提升。

2.1 中间信道的选取

在LDPC-极化码级联码中，使用LDPC对中间信道传输的信息比特进行额外保护。选择一部分信息比特进行LDPC编码，将经过编码的LDPC码字送入中间信道传输，将未编码的信息比特送入极化码的“好信道”传输。因此，需要选择易错的信道作为被保护的中间信道。

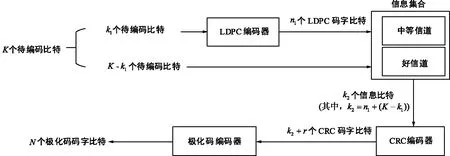
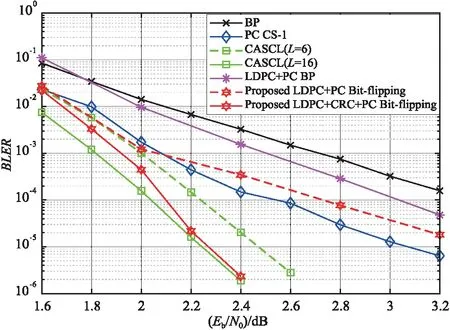
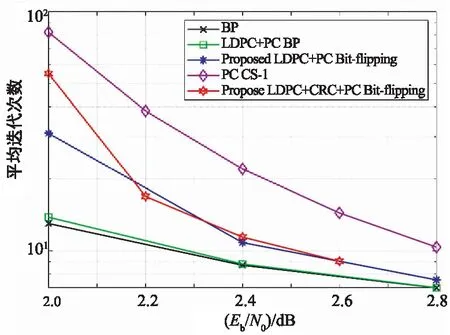
文献[11]中选择巴氏参数值δ1

中间信道的选取步骤如下：

① 首先将信息集合A中所有元素分成不同的子集Ai,Aj...，其中，同一个子集中的元素对应GN中的行有相同的行重w，且wi=wj。

② 在同一个子集Ak内，按信道对应的Pe(ui)从高到低排列元素。

③ 选择{Ai,Aj...}中前n1个信道作为中间信道。(n1是中间信道的个数，也等于选用的LDPC码字的码长)。

2.2 联合因子图BP算法早停机制

对LDPC-极化码使用联合因子图译码时，为了减少平均迭代次数以及译码时延，需要设定合理的早停机制。极化码常见的早停机制有：CRC判决和G矩阵判决。由于没有使用CRC级联，并且G矩阵判决只能帮助判断BP译码过程是否收敛，无法判断收敛结果的正确性。为了进行可靠且高效的早停判断，充分利用LDPC-极化码级联码的结构特征，结合LDPC码的H矩阵和极化码的G矩阵，进行早停判断的双重保护。

联合因子图BP译码的流程图如图4所示，从图中可以看出：在LDPC的BP译码结束后开始早停判断，只有当LDPC的H矩阵校验和极化码的G矩阵校验都成功，才进行早停；否则继续迭代更新信息，直到达到最大迭代次数。

图4 联合因子图的BP译码Fig.4 Flow chart of proposed joint factor graph BP decoding algorithm

2.3 比特翻转译码算法

在联合因子图的BP译码失败后，使用比特翻转算法对易错集合CS中的元素的先验LLR翻转。如图5所示，此时设定一个最大迭代次数m，任意一次翻转成功或者达到最大迭代次数都会导致译码结束。

图5 LDPC-极化码比特翻转译码算法Fig.5 Flow chart of proposed LDPC-Polar codes bit-flipping decoding algorithm

基于比特翻转算法的LDPC-极化码级联码有很好的译码性能，与较低的平均迭代次数与时延，但是，由于该级联结构还有大量的信息比特只是经过G矩阵校验，而G矩阵只能验证极化码是否收敛，无法判断收敛的正确性。因此，此级联码极易在多次迭代后收敛到错误的码字。在下一部分，通过与CRC构成三级级联码来帮助校验所得码字的正确性。

3 LDPC-CRC-极化码三级级联码

CA-SCL译码器利用CRC优秀的纠错能力获得了非凡的BLER性能。在这部分，通过将LDPC-极化码与CRC的级联构成一个三级串行级联码，通过CRC优秀的纠错性能，结合上一部分提出的比特翻转译码算法，进一步提升了BLER性能。LDPC-CRC-极化码三级级联码的编译码流程如图6所示。

图6 LDPC-CRC-极化码的编译码流程图Fig.6 Flow chart of encoding and decoding for LDPC-CRC-Polar codes

信息比特首先经过LDPC编码，CRC编码，极化码编码，然后将得到的编码码字送入信道，信号接收端通过联合BP比特翻转译码算法进行译码。

3.1 LDPC-CRC-极化码的编码

码长为N，信息比特数为K的级联码编码过程如图7所示，编码步骤为：

图7 LDPC-CRC-极化码三级级联码编码Fig.7 Encoding of concatenated LDPC-CRC-Polar codes

① 取出K个待编码信息比特中的前k1个比特，使用(n1,k1) LDPC码编码。

② 将n1个LDPC码字比特输入中等信道，将剩余K-k1个待编码信息比特输入好信道的前K-k1个信道。

③ 将极化码的信息集合A中已输入的k2个信息比特(中等信道中所有比特与好信道中前K-k1个信道中的比特)进行(k2+r,k2) CRC码的编码，得到的r个校验比特输入好信道中未使用的最后r个信道(r是CRC的校验比特数)。

④ 将极化码的冻结集合Ac中的冻结比特置0，得到极化码信息比特uN1=(u1,u2,...,uN)。使用(N,k2+r)极化码对uN1=(u1,u2,...,uN)进行编码，得到了码长为N的LDPC-CRC-极化码三级级联码的码字xN1=(x1,x2,...,xN)。

3.2 LDPC-CRC-极化码的译码算法

使用第2部分提出的改进的比特翻转译码算法对三级级联码进行译码。与LDPC-极化码的译码算法区别在于，在三级级联码中，使用CRC校验与LDPC的H矩阵进行早停判断，这种情况下早停判断的可靠性得到了极大地提高。

4 仿真结果

对上文提出的2种级联码的译码算法性能进行仿真,为了保证各译码算法之间对比的公平性，保持码字的码长和有效码率不变，即：N=2 048,K=1 024。

对于LDPC-极化码级联码P(2048,1024+32)使用(64,32)的Mackay码作为LDPC外码，此时k1=32,n1=64，中等信道的个数为64，好信道的个数为1 024-32=992。对于LDPC-CRC-极化码三级级联码P(2048,1024+32+24)，使用生成矩阵为g(x)=x24+x23+x6+x5+x+1的CRC-24码作为CRC编码，此时好信道的个数为1 024-32+24=1 016。极化码的构造算法选择高斯近似算法，设计信噪比为2.5 dB。所有BP译码算法的最大迭代次数都是100。

同时，使用BP译码算法下的P(2048,1024)，文献[13]中提到的中间信道LDPC-极化码P(2048,1024+32)，文献[10]中提到的CS-1译码算法下的P(2048,1024+24)，CA-SCL译码算法[5]下的极化码P(2048,1024+24)的BLER性能进行对照。

根据图8可以看出，文中提出的改进的LDPC-极化码比特加强译码算法的BLER性能优于文献[13]中BP译码算法下的中间信道LDPC-极化码，例如，在BLER=10-4处的P(2048,1024+32)，比BP译码算法下的中间信道的LDPC-极化码有0.3 dB的增益。但是由于缺少了CRC优秀的纠错性能，其BLER性能不如文献[10]中提出的基于CS-1译码的P(2048,1024+24)。

图8 P(2048,1024) 各译码算法的BLER性能对比Fig.8 BLER performance of different decoding algorithms for P(2048,1024)

然而，文中提出的LDPC-CRC-极化码三级级联码P(2048,1024+32+24)在比特翻转译码算法下拥有极其优异的性能。在BLER=10-5处的P(2048,1024+32+24)，比基于CS-1译码的P(2048,1024+24)有0.7 dB的增益。在中高信噪比区间，接近基于CA-SCL(L=16)译码器的P(2048,1024+24)的BLER性能。

除了优异的BLER性能，本级联码在比特翻转译码算法下有较低的平均译码迭代次数。从图9可以看出，在BP译码器的最大迭代次数都设为100的情况下，在中高信噪比区间，本文提出的2种基于比特翻转译码算法的级联码P(2048,1024+32)和P(2048,1024+32+24)平均迭代次数相近，且都比文献[10]中提出的极化码的CS-1译码算法的平均迭代次数要低很多。

图9 P(2048,1024)各译码算法的平均迭代次数对比Fig.9 Average numbers of iterations of different decoding algorithm for P(2048,1024)

相较于文献[10]中的CS-1算法与CA-SCL算法，本算法还有较低的译码时延。表1比较了不同算法的译码时钟周期数，在中高信噪比区间，LDPC-CRC-极化码三级级联码P(2048,1024+32+24)在比特翻转译码算法下的译码时钟数与CS-1算法相比，降低了30%～50%。

表1 P(2048,1024)极化码的译码时钟数比较Tab.1 Average decoding clock cycles of different decoders for P(2048,1024)

5 结论

与BPF和BPL等通过增加译码复杂度提高BLER性能的算法不同，本文寻求对极化码的编码进行改进，通过级联其他优异的码字，在保持低时延的同时，获得更优异的译码性能。在对LDPC-极化码级联码进行比特翻转译码时，其BLER性能较BP译码算法下的LDPC-极化码有0.3 dB的增益。在此基础上，本文首次将LDPC-极化码与CRC级联形成一种LDPC-CRC-极化码三级级联码，比特翻转译码算法下BLER性能比极化码的CS-1译码算法有0.7 dB的增益。尽管级联码带来不错的译码性能，也不能忽视级联码的劣势，即额外的编译码复杂度以及额外的硬件开销。但是，在某些对性能和时延要求较高的场景下，本级联码的优势是突出的。