基于斐波那契数列短码长QC-LDPC码的构造

杨卫国,郑 麟

(海军航空工程学院,山东 烟台 264001)

基于斐波那契数列短码长QC-LDPC码的构造

杨卫国,郑 麟

(海军航空工程学院,山东 烟台 264001)

设计了一种QC-LDPC码的校验矩阵构造方法,矩阵的信息位根据斐波那契数列进行构造,校验位根据IEEE802.16e标准中码字的校验矩阵进行构造,这样构造的校验矩阵具有准双对角线结构,在编码过程中可以采用快速编码算法,降低了编码复杂度，同时节省了存储空间。通过仿真,该方法构造的码字在中短码范围内较Gallager码性能良好,并且通过改变循环矩阵的大小,可以获得码性能较好的多种码长的码字,码长选择范围较大。

QC-LDPC码; 快速编码算法; 斐波那契额数列; IEEE802.16e; 短码

郑 麟(1992-),男,硕士研究生。

LDPC码(低密度奇偶校验码)是一种可以逼近香农极限的码,虽然在1962年Gallager博士刚刚提出时并未受到人们的关注,但在后期的研究发展过程中,LDPC码优异的性能越来越被人们认可,现在已被广泛应用。LDPC码目前研究的重点大部分集中在检验矩阵的构造和改进译码算法上,而构造性能优异的校验矩阵对于提高码字性能,降低译码复杂度,都有重要意义。

LDPC码根据构造方式可分为随机构造法和结构化构造法。随机构造法以Gallager随机构造法[1]和Mackay随机构造法[2]为代表,编码思想简单,纠错性能良好,但其编码复杂度较高,而结构化构造的码字可以较好地解决编译码复杂度的问题且不失码字性能。

QC-LDPC码(准循环LDPC码)是目前研究较多的一种结构化构造码,该种码字占用存储空间少,编译码复杂度低,纠错性能良好,已被IEEE802.16e标准采用。本文以IEEE802.16e标准中的编码方案为基础,利用斐波那契数列的性质构造理论上可以适用于多种码长的QC-LDPC码(F-QC-LDPC码)。

1 IEEE802.16e标准中的LDPC码

IEEE802.16e标准规定的LDPC码总共有19种码长,每种码长都有4种码率,具体见表1。

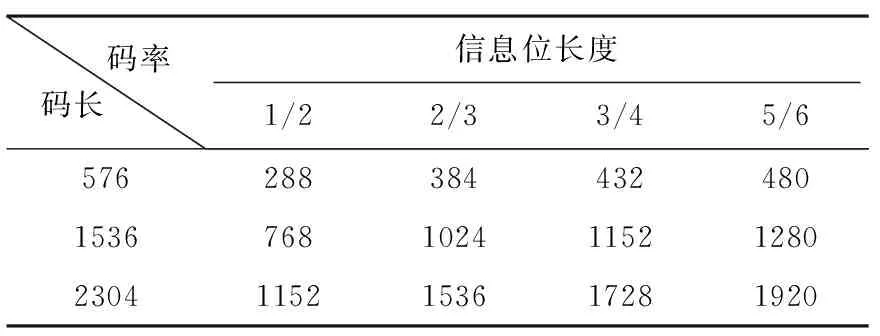
表1 IEEE802.16e标准的三种码长不同码率下的信息位长度

QC-LDPC码的校验矩阵由基矩阵Hbm×n来表示,基矩阵中每个元素表示z×z的循环矩阵右移Hb(i,j)位后生成的矩阵。802.16e标准中的基矩阵是固定的,大小为12×24,循环矩阵的大小z=N/24,N为码长即扩展后校验矩阵的列数。802.16e标准中的基矩阵Hb12×24如表2所示。从表中可以看出,基矩阵Hb右半边为准双对角线结构,这种结构的校验矩阵在编码时采用快速编码方法,可以不借助生成矩阵直接生成码字。矩阵中“-1”表示z×z大小的全零矩阵。

2 快速编码方法

IEEE802.16e标准采用的编码算法为快速编码算法,以1/2码率为例,简单介绍快速编码算法的原理。

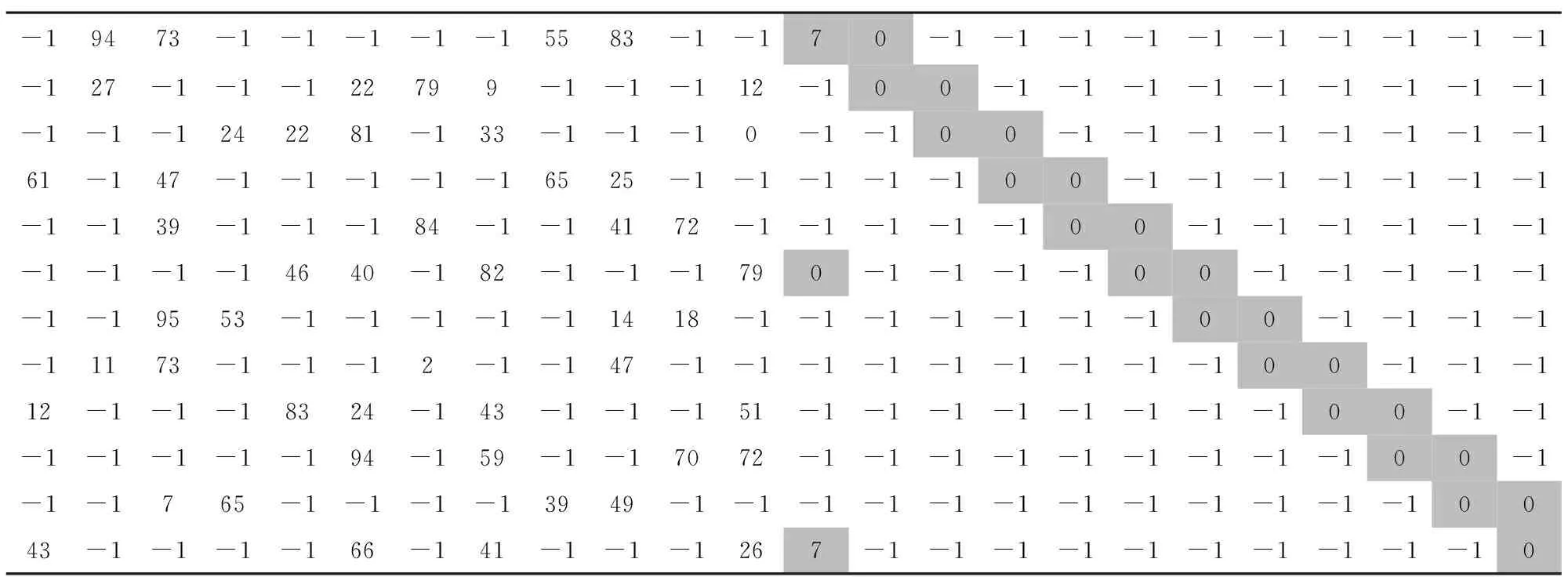
表2 IEEE802.16e标准中的基矩阵

若编码后输出的码字为C=(c1,c2,…cn),由于码字为系统码,所以前n/2项为信息位,后n/2项为校验位。假设信息比特S=(s1,s2,…s5),校验比特为J=(j1,j2,…j5),则编码输出为C=[SJ],由于信息比特已知,要求编码后的码字就是求校验比特J。根据校验等式H·CT=0可得:

(1)

快速编码中采用的检验矩阵H同样采用准双对角线结构,因此

(2)

运算在GF(2)上进行,由式(1)和式(2)可得：

(3)

解式(3)得

(4)

由此求得

(5)

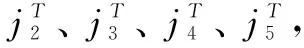
3 基于斐波那契数列的QC-LDPC码构造

3.1 斐波那契数列的定义

斐波那契数列又称黄金分割数列,该数列以0、1开始,随后的数字是前两项之和,表现成递推公式为

F(0)=0,F(1)=1,

F(n)=F(n-1)+F(n-2),(n≥2,n∈N*)

(6)

具体表示为如下数列:

0,1,1,2,3,5,8,13,21,34,55,89,144,…

斐波那契数列在现代物理、准晶体结构、化学等领域都有直接的应用,这样一个完全是自然数的数列其通项公式确是无理数表示,且随着n的增大,前后项比值趋近黄金分割0.618,而且自然界中好多事物的规律都趋于这个数列,鉴于其如此多的优良性质,考虑用其构造校验矩阵。

3.2 基于斐波那契数列的QC-LDPC码构造方法

以IEEE802.16e标准中的校验矩阵为基础构造基矩阵的校验位,并根据斐波那契数列合理构造基矩阵的信息位,因主要针对中短码,所以基矩阵的维数定为5×10,码率定为1/2,具体方式如下:

1)构造基矩阵Hb=[HvHc],其中

(7)

是一个具有准双对角线结构的矩阵;

2)构造Hv,矩阵Hv的第一行全部为0,第一列的数字为斐波那契数列的奇数项,即0,1,3,8,21,除第一行外,每行根据行首数字依次向后排列写出斐波那契数列,构造好的Hv如下所示：

(8)

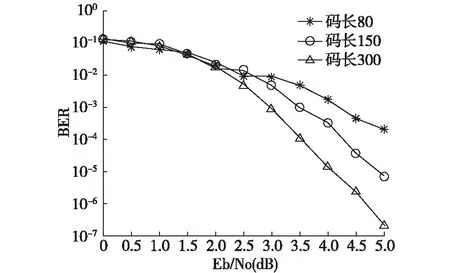
3)更新矩阵Hv,循环矩阵的大小z=N/10,N为码长,当z

4)根据最后构造好的基矩阵Hb,将-1替换为z×z大小的全零矩阵,其他元素替换为z×z大小的单位矩阵向右循环移动Hb(i,j)位所得到的矩阵,按照快速编码算法进行编码。

QC-LDPC码在存储过程中主要存储其校验矩阵,通过本文提供的编码方法可知,F-QC-LDPC码在存储过程中除了需要完全存储矩阵Hc外,矩阵Hv只需存储0和1两个元素,其他元素均可通过斐波那契数列的性质求得,很大程度上节省了编码器的存储空间,且可以根据需要任意设定码长(码长是10的倍数,码率为1/2)。

4 性能分析

本文是为了设计性能优良的中短码,在仿真中选取码长为250,此时循环矩阵的大小z=250/10=25,根据矩阵构造F-QC-LDPC码,对编码输出采用BPSK调制,传输信道选用AWGN信道,译码算法采用和积译码算法,信噪比从0增加至5,对比码字采用Gallager随机构造法构造,码长为256,两种码字的码率均取1/2,最大迭代次数为30次,仿真结果如图1所示。

图1 Gallager码与F-QC-LDPC码性能比较

由图1可见,在信噪比较低的情况下,两种码字的性能相差无几,在信噪比达到3时,F-QC-LDPC码的误码率就比Gallager码高出将近一个数量级,在误码率为10-5时,F-QC-LDPC码有将近1dB的增益。

单独比较F-QC-LDPC码在不同码长情况下的译码性能,仍然采用BPSK调制,传输信道为AWGN信道,译码算法为最大迭代次数30的和积译码算法,码长分别取80,150,300进行仿真,仿真结果如图2所示。从图中可以看出,利用本文方法构造的LDPC码在码长为80的超短码时性能并不是特别理想,但中短码性能比较好,码长300时在信噪比较大的情况下,误码率就可以达到10-7数量级。

图2 不同码长F-QC-LDPC码性能比较

当F-QC-LDPC码码长达到2000,z=200时,同样在BPSK调制下通过AWGN信道,与IEEE802.16e标准下的QC-LDPC码选取其固定码长2016,码率1/2的情况下进行比较,经过30次迭代的和积译码后的仿真结果如图3所示。

图3 码长2000的F-QC-LDPC码与码长2016的IEEE802.16e标准码性能比较

如图3所示,F-QC-LDPC码与IEEE802.16e标准码在码性能上存在一定差距,分析其原因主要是因为F-QC-LDPC码的校验矩阵并未进行消环处理,校验矩阵中存在一定数量的4环和6环,影响了F-QC-LDPC码的译码性能,但差距并不是特别大,在误码率为10-5时,两者仅相差约0.3dB。比较图1和图3就会发现,本文所提出的码在未消环的情况下仍能获得比Gallager码更优异的码性能。

5 结束语

本文提出了一种基于斐波那契数列构造的QC-LDPC码的基矩阵,该码可以采用IEEE802.16e标准的快速编码方案进行编码,编码速度快,同时由于矩阵中元素存在数列性质,很大程度上节省了存储空间,通过仿真结果表明,用此种方法构造的LDPC码在不消环的情况下,中短码就拥有比较优异的性能,且码长可选范围较大,具有一定的研究参考价值,在此方法基础上,如果可以消除短环将会获得更加优良的码性能。

[1] Gallager R G.Low-density parity-check codes[J].IEEE Transactions on Information Theory,1962,8(1):21-28.

[2] MacKay D J C.Good error-correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory,1999,45(2):399-431.

[3] 黄胜,穆攀,张睿,等.基于大衍数列的规则QC-LDPC码构造方法[J].电视技术,2016,40(9):77-80,94.

[4] 易旭,杜昊阳.LDPC码的研究进展和应用展望[J].通信技术,2016,49(1):1-6.

[5] Fossorier M P C.Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J].IEEE Transactions on Information Theory,2004,50(8):1788-1793.

[6] Tanner R M,Sridhara D,et al.LDPC block and convolutional codes Based on circulant matrices[J].IEEE Transactions on Information Theory,2004,50(12):2966-2984.

[7] Gallager R.Low-Density Parity-Check Codes[M],Cambridge,M A:MIT Press,1963.

[8] MA Ke-xiang,ZHANG Peng.Low-Delay Loop Detection Algorithm for LDPC Codes[J].Journal of CAEIT,2015(4):341-343.

[9] Chen X,Kang J,Lin s,et al.Memory System Optimization for FPGA-Based Implementation of Quasi-Cyclic LDPC Codes Decoders[J].Circuits and Systems I:Regular Papers,IEEE Transactions,2011(58):98-111.

[10] Ardakani M,and Kschischang F R.A More Accurate One-Dimensional Analysis and Design of Irregular LDPC codes[J].IEEE Transactions on Communications,2004:52(12):2106-2114.

A Construction Method of QC-LDPC Codes Based on the Fbonacci Sequence

YANG Wei-guo,ZHENG Lin

(Navy Aeronautics and Astronautics University,Yantai 264001,China)

This paper presents a construction method of quasi-cyclic low-density party-check(QC-LDPC) codes,whose information parts are based on the Fbonacci sequence while the check parts are based on IEEE802.16e standard.Because of the quasi dual-diagonal structure,it can lower the complexity and save the memory space through fast encoding algorithm.Simulation results show that the proposed codes is better than Gallager codes when the code length is shorter.Besides,there are many good codes at a lot of length by changing the size of the cyclic matrix.

QC-LDPC codes; fast encoding algorithm; Fbonacci sequence; IEEE802.16e; short codes

TN911.22；E96

A

10.3969/j.issn.1673-3819.2017.05.027

1673-3819(2017)05-0130-04

2017-06-26

2017-08-06

杨卫国(1987-),男,山东烟台人,硕士研究生,研究方向为信道编码。