指向空间思维能力提升的多维度数形结合策略与研究

摘 要：数形结合是小学数学教学的基本思想方法，其能有效发散学生的数学思维和提高课堂教学效率。在实践中，文章作者发现学生的空间想象能力还不够成熟，对枯燥的算式和数字有厌倦感，遇到难题也不会通过画图来帮助理解，但数形结合的教学策略可将抽象的知识具体化，使学生易接受。基于此，文章拟建构一个多维度数形结合思想进行阐述。

关键词：数形结合;空间思维;多维度

作者简介：李红英（1969.11—），女，浙江杭州人，浙江省杭州市富阳区受降小学，一级教师，本科，研究方向：小学数学教学。

一、现象与归因

（一）看现象：数形结合思想的直观情况

小学低中段学生的学习特点是以兴趣为主，数学教材往往以与实际生活情境相关的符号、图形、故事为主进行编排，并没有真正关注数量关系。大多数学生不能结合图文完整地表述题目的含义，找出的数学信息不全，建立数量关系时乱凑数，解题过程中缺乏空间想象。高段学生在解决问题时多数没有将新旧知识联系起来，未能思考现实中的数量关系和建构空间模式，无法树立起数形结合思想。那么如何让不同学段的学生去理解不同的视图内容？如何让数形结合思想在实践操作中得到灵活有效的运用？这些问题都是笔者在本文中将要探讨的话题。

（二）剖实质：数形结合思想在课堂实践应用中存在的问题

1.学生方面

第一，学生对数形结合的知识掌握和方法掌握不够，主要表现在两方面：一是将图形转化成数;二是将数或式转化成图形。学生在实际做题中，往往没有建构起数形结合思想的概念，而是直接以数或式代形，导致解题受限，思维难以发散。

第二，学生思想上固有的依赖性。在日常教学中，学生对教师的作图依赖性很强，导致在平时的作业中，不肯作图或不能规范作图。

2.教师方面

教师一般认为数形结合思想没有算理和算法重要，无意识地忽视了数形结合思想，对此降低或不作要求。目标不明，则动力不足。

二、思考与设想

（一）数形结合的概念

数形结合就是把抽象的语言、数量关系与直观的几何图形、位置关系结合起来，通过以形助数或以数解形，使复杂的问题简单化、抽象的问题具体化，从而实现优化解题途径的目的。

（二）多维度的数形结合思想理念的意义

1.数形融合，理解文字内涵

在数学学习中，文字题占有很大比例，它是用文字表达数与数、数与形之间运算关系的题目，因此通过题目解读结合数形以及思维的模式，就可以有效降低解题难度。所以为了让学生理解题中的数量关系，我们应尽可能将语言文字转化成图形，将抽象的语言文字形象化。

2.数形链接，构建空间概念

在几何形体的教学中，教师可以先拿出与教学内容相关的几何形体的直观教具，让学生观察、体验一下该几何体的形状、外形特征等，直接感知该几何形体的直观属性，从而对所学内容有直观的认识。

3.数形对比，厘清数量关系

动手操作可促使学生由具体形象思维向抽象逻辑思维过渡。如果把抽象的知识转化为看得见、摸得着、容易理解的知识，把要理解的知识点变得简单化并生动有趣地呈现出来，就可以有效激发学生的学习兴趣。

4.数形互补，提炼多种算法

在小学数学教学中，要鼓励算法的多样化。但算法多样化并非一定要从中选优、优中选精，只要能体现学生自己的思维方式，都应鼓励他们多加提炼。算法多样化是对学生个性化学习的尊重，也有利于学生之间的交流，同时也锻炼了学生的高水平思维能力。

三、数形结合思想的实践探究

（一）以形思數

1.在直观中理解数

数学概念比较抽象，教学中，教师常常用数形结合思想开展教学，利用学生对图形与数字之间的联系，让学生的思考建立在对图形的认识、对数字的理解上。同时，教师通过渗透数形结合思想，实现了学生思维的多样化。

【案例1】折出不同的面积为  的正方形。

（1）折出一个正方形，并且这个正方形的面积是原来正方形面积的  。给你的同学解释一下，你折出的图形面积为什么是原来面积的  。

（2）再折出一个三角形，并且这个三角形的面积是原来正方形面积的  。给你的同桌解释一下，你折出的图形面积为什么是原来面积的  ，但这些三角形的形状与前面折出的三角形的形状是不同的。

利用手中的正方形纸片，借助日常生活经验与数学活动经验，学生能折出步骤1、步骤2要求的正方形与三角形（见图1、图2），这是较低层级思维的思考。当学生被要求折出新的三角形，且面积是原来正方形的  时，或面积是原来正方形的  时，学生也能借助直觉折出步骤3、步骤4要求的正方形与三角形（见图3、图4），学生也能借助数学推理向同桌解释数学依据，这是中高层级思维的思考。

2.明析数量关系

在低段数学教学中，图文式题目占有很大比例，主要是用文字表达数与数、数与形之间的运算关系。因此，学生合理利用数形结合想，对解题帮助很大。

【案例2】菜园里有15只小鸡，还有8条小虫，小鸡比小虫多多少？（用实物图片摆）

从图5中可清楚地看到，上面一行小鸡比下面一行小虫多，可把上面一行的小鸡分为两部分：一部分是一小虫同样多的，另一部分剩下的，只要把小鸡和小虫的数量一一对应，余下的就是小鸡比小虫多的数量。

练习变式：小鸡加1只变成16只，小虫加1条变成9条，那么小鸡比小虫多多少？

低层级思维的学生就是从16数，一只一只减少9，相差7，这样算既麻烦又易错。

中层级思维的学生就是16先减6等于10，再减3等于7。

高层级思维的学生是就16减少1就是15，9减少1就是8，刚刚我们学过15-8等于7。

这种高层级思维可能源于小虫的数量怎样比小鸡少，也可能源于对于减法的感性认知，即差不变的性质。

不同的算法，源于学生的数感。他们选择这样算，可能源于小虫的数量怎样比小鸡少的一种数学比照，可能源于对朦胧的减法性质的感知，明确了数量关系，即被减数和减数同时减去一个相同的数，差不变。

3.帮助学生有序思考

【案例3】下面□的数量有怎样的变化规律？第20个图形有几个□？

通过摆小木块方式探究的学生，多数是将木块放在图形顶层，少部分放在右侧（见图6、图7）。而采用画图方式的学生，增加的正方形几乎全部摆在底层（见图8）。学生能列出算式1+3+5+…+n，但第20个图形的底层有多少个，运算有难度。

低层级思维的学生能够根据变化规律逐步数出第20层有39个。

中层级思维的学生能够根据观察得出底层图形数量的规律是：层数×2-1=底层图形的数量。

高层级思维的学生能够利用剪切平移法，将不规则的图形想象成正方形（如图9）。

最后得出结论：第20个图形☐数量的算法是：1+3+5+…37+39=20×20。

儿童的认识规律，一般来说是从直接感知到表象再到形成科学概念的过程。通过形转化为数，学生拓展了对本部分知识学习的深度，一方面对将数转化为形的知识进行巩固，另一方面又提升了逆向思考、发散性思维的能力。

（二）以数想形

1.引导学生在转换中建立“形”

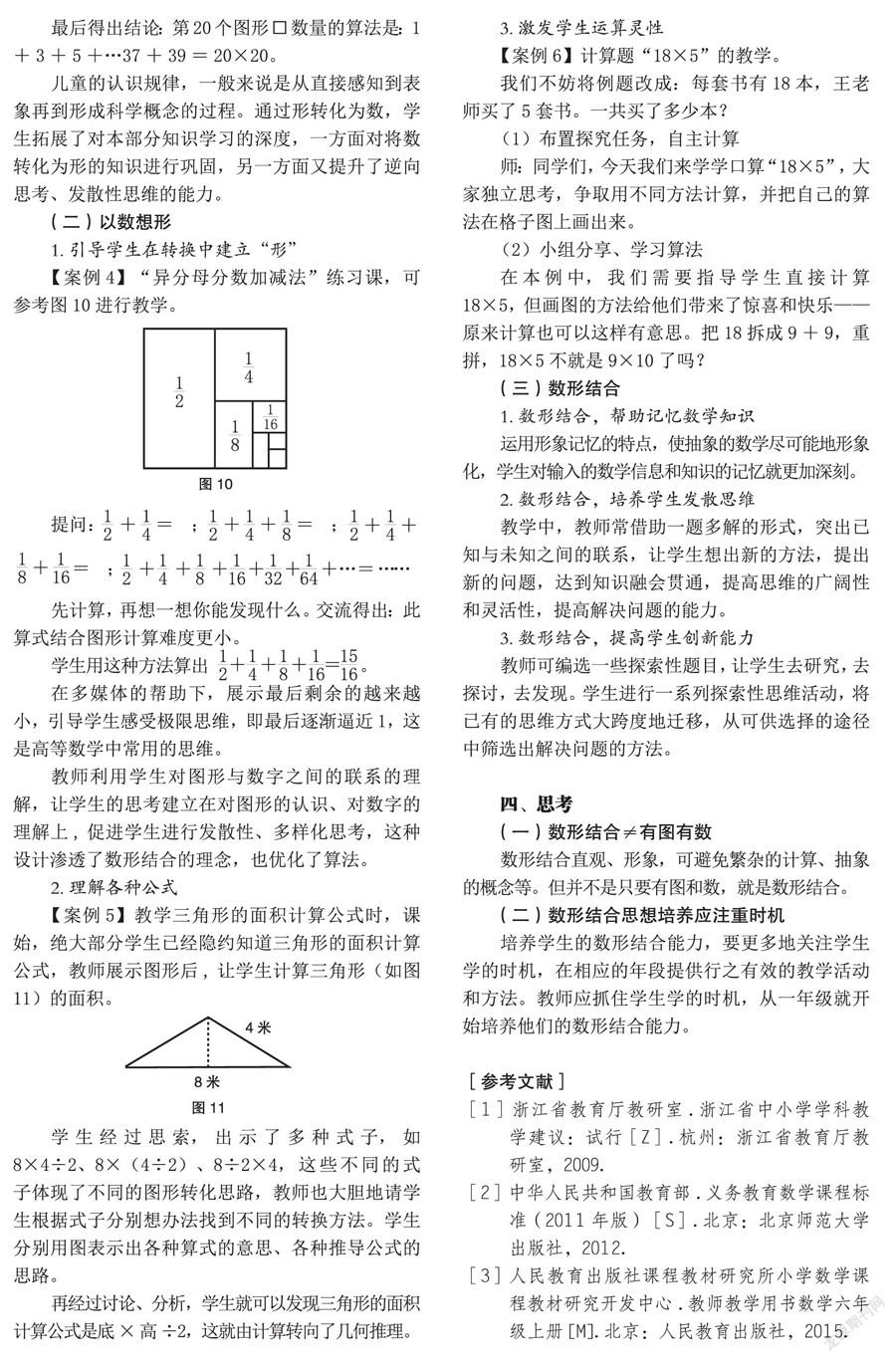
【案例4】“异分母分数加减法”练习课，可参考图10进行教学。

先计算，再想一想你能发现什么。交流得出：此算式结合图形计算难度更小。

学生用这种方法算出                  。

在多媒体的帮助下，展示最后剩余的越来越小，引导学生感受极限思维，即最后逐渐逼近1，这是高等数学中常用的思维。

教师利用学生对图形与数字之间的联系的理解，让学生的思考建立在对图形的认识、对数字的理解上，促进学生进行发散性、多样化思考，这种设计渗透了数形结合的理念，也优化了算法。

2.理解各种公式

【案例5】教学三角形的面积计算公式时，课始，绝大部分学生已经隐约知道三角形的面积计算公式，教师展示图形后，让学生计算三角形（如图11）的面积。

学生经过思索，出示了多种式子，如8×4÷2、8×（4÷2）、8÷2×4，这些不同的式子体现了不同的图形转化思路，教师也大胆地请学生根据式子分别想办法找到不同的转换方法。学生分别用图表示出各种算式的意思、各种推导公式的思路。

再经过讨论、分析，学生就可以发现三角形的面积计算公式是底×高÷2，这就由计算转向了几何推理。

3.激发学生运算灵性

【案例6】计算题“18×5”的教学。

我们不妨将例题改成：每套书有18本，王老师买了5套书。一共买了多少本？

（1）布置探究任务，自主计算

师：同学们，今天我们来学学口算“18×5”，大家独立思考，争取用不同方法計算，并把自己的算法在格子图上画出来。

（2）小组分享、学习算法

在本例中，我们需要指导学生直接计算18×5，但画图的方法给他们带来了惊喜和快乐——原来计算也可以这样有意思。把18拆成9+9，重拼，18×5不就是9×10了吗？

（三）数形结合

1.数形结合，帮助记忆数学知识

运用形象记忆的特点，使抽象的数学尽可能地形象化，学生对输入的数学信息和知识的记忆就更加深刻。

2.数形结合，培养学生发散思维

教学中，教师常借助一题多解的形式，突出已知与未知之间的联系，让学生想出新的方法，提出新的问题，达到知识融会贯通，提高思维的广阔性和灵活性，提高解决问题的能力。

3.数形结合，提高学生创新能力

教师可编选一些探索性题目，让学生去研究，去探讨，去发现。学生进行一系列探索性思维活动，将已有的思维方式大跨度地迁移，从可供选择的途径中筛选出解决问题的方法。

四、思考

（一）数形结合≠有图有数

数形结合直观、形象，可避免繁杂的计算、抽象的概念等。但并不是只要有图和数，就是数形结合。

（二）数形结合思想培养应注重时机

培养学生的数形结合能力，要更多地关注学生学的时机，在相应的年段提供行之有效的教学活动和方法。教师应抓住学生学的时机，从一年级就开始培养他们的数形结合能力。

[参考文献]

[1]浙江省教育厅教研室.浙江省中小学学科教学建议：试行[Z].杭州：浙江省教育厅教研室，2009.

[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[3]人民教育出版社课程教材研究所小学数学课程教材研究开发中心.教师教学用书数学六年级上册[M].北京：人民教育出版社，2015.