含积分式方程的解的研究

李 高

(大同大学 数学与计算机科学学院，山西 大同 037007)

当遇到含积分式的方程求解时，求解者似乎感到很棘手。其实含积分式的方程中的积分不外乎两类：一类是定积分，另一类为变限函数[1]。下面逐一探求其解法。

1 积分式为定积分

1.1 传统的代入法求解

由于定积分是一个数值，所以这类积分亦可采用代入法确定定积分的值，便可求得解。

f(x)=x+2A

代入原方程，得

f(x)=x+1+4A

则

故

f(x)=x-1

1.2 取积分法求解

由定积分概念知：定积分是一个数值，因此关于这类方程的求解方法一般是方程两边同时取该积分区间的定积分，求出该定积分即得方程的解[5-9]。

例2 对例1利用取积分法求解。

解法二 原方程等式两端取积分得

代入原方程，得

f(x)=x-1

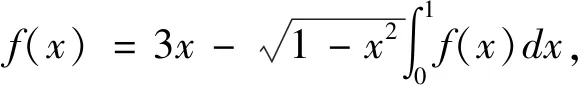
即

所以

故

1.3 求导数法求解

定积分的导数为零。因此，关于这类方程的求解方法一般是方程两边同时对自变量求导，可得关于所求函数的微分方程，再解微分方程，即得所求解。

例4 对例1利用求导法求解。

解法三 原方程等式两端同时对x求导，得

f′(x)=1

则

f(x)=x+c

将其代入原方程，得

c=-1

故

f(x)=x-1

2 积分式为变限函数

由于积分变限函数都可以利用定积分的概念转化为积分变上限函数，并有下面定理。

因此，求这类方程的解一般是方程两边同时对自变量求导，去掉积分变限函数，可得关于所求函数的微分方程，再通过求解微分方程得所求解。

解 因为方程

变形为

对上式求导，得

再求导得二阶常系数非齐次线性微分方程

φ″(x)=ex-φ(x)

即

φ″(x)+φ(x)=ex

特征方程为

λ2+1=0

特征根为

λ=±i

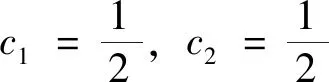
故