基于模糊相容关系的公共卫生应急决策模型设计

张 卫 东

(皖西卫生职业学院,安徽 六安 237000)

0 引 言

公共卫生应急决策模型建立的目的，是当遭遇突发性公共卫生事件时，可以在较短的时间里掌握当前受影响地区的受影响情况，解决需要的应急物资等问题，帮助决策者进行应急决策[1]。目前对应急决策模型的研究得到了重视，应急决策模型也由仅得到针对受影响地区的不同严重性的结论，发展到目前可以给出一个应急框架[2]。目前所研究的常见应急决策模型如依靠态势预测的决策模型，即依据对事件发展态势的判断得出决策结论，以及依据Pawlak粗糙集来给出具体决策结论的决策模型。但这些常见的应急决策模型中集合间缺乏容错机制，实际应用时无法在不确定因素中发现相关信息。而模糊相容关系可以在集合中给出一定的包含关系从而使模型中集合存在一定的延伸，有助于提高模型决策精度[3]。

1 模型设计

1.1 使用模糊相容关系建立模型粗糙集

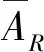
(1)

(2)

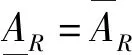
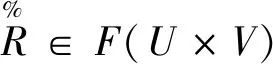
(3)

(4)

而当α=1时，根据(4)运算，则会出现

(5)

R∈P(U×V)(P(U))

(6)

(6)式中P表示为所有子集。在基于模糊相容关系的模糊粗糙集中当U=V时会退化成单个论域上的双量化模糊粗糙集。而另一个论域V={y1,y2,…,yn}代表在公共卫生事件发生后，产生影响的特征指标集。可以详细表示为经济损失、发病人数等[5]。一般公共事件的一般影响特征指标可以看做一种收益型的指标[6]。建立模糊相容粗糙集后，在此基础上进行公共卫生模型建立。

1.2 事件发展态势评估

在应急决策模型中，首先要对出现的事件发展趋势做出一定的趋势评估，可以通过马尔科夫预测方法[7]。在经过事件的k阶段，转移从事件态势i向着事件态势j的概率为

T(xi+k=j|xi=i)=Tij(k)(i,j=1,2,…,e)

(7)

在(7)式中t代表评判标准权重。评判标准权重数值根据实际事件情况来拟定[8]。k代表目前部门执行应对方案对事件态势的改善权重，同时制定状态转移矩阵

(8)

根据初始概率T1=(Tx11,Tx22,…,Txn1)，可推出

Tn=(Tx1e,Tx2e,…,Txee)

(9)

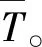
(10)

(11)

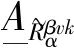
1.3 应急物资需求与多部门协同决策

在判断地区受事件影响后，要对应急物资进行需求预测。对受事件影响地域的物资需求预测计算如下

Z=DlQlFl-δCj

(12)

在(12)式中，Z代表当前事件后的应急物资的最小需求量，Fl表示当前受公共卫生事件所影响的状况，如受疾病感染人数、受污染影响人数等。Dl表示受影响地区的系数，Ql代表受影响地区的气候系数，Cj为应对突发公共卫生事件而存储的应急物资数量，δ表示应急物资在事件发生时的保全率。而在应急资源的分配以及对当前事件的决策时，需要多个应急管理部门执行一个协同决策网络[10]。协同应急决策网络如图1所示。

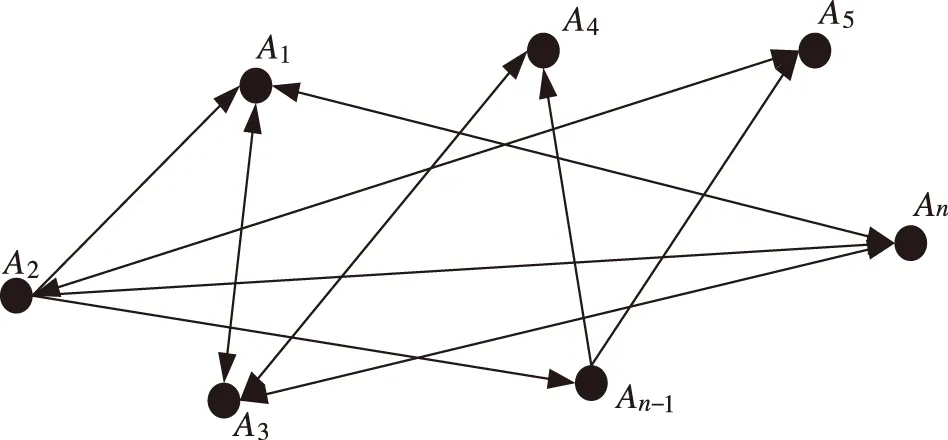
图1 多应急决策部门决策协同网络

图1中，当部门A2的决策影响部门A1的决策时，则A2与A1之间存在一条有向边，而A1与A3决策相互影响时，则体现为双向边[11]。而该协同网络部门之间的影响会根据当前公共卫生事件的严重程度、种类等因素发生改变[12]。对实际的协同决策网络可以使用协同关系矩阵Sk进行描述：

(13)

在(13)中，sij表示部门Ai与Aj的决策协同关系，因协同决策的相互影响关系在有些事件中会发生改变，因此Sk矩阵在实际中可能出现非对称的情况。各部门之间决策协同的情况也会在公共卫生事件发生时受到影响[13]。

1.4 应急决策结论

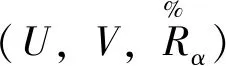
(14)

式(14)中在精度参数为α的条件下，所有受到公共卫生安全事件影响的受灾地区的指标函数MMD(最大均值差异)值为xi。而受灾地区的指标函数要根据当前不同的公共卫生决策问题来对指标函数进行具体的定义。

2 实验论证分析

为了验证设计的应急决策模型的可行性，使用SARS事件来进行模型的模拟应用，并使用文献[14]和文献[15]中的模型以及传统使用Pawlak经典粗糙集建立的应急决策模型与本文模型进行对比。

2.1 实验数据准备

实验使用曾在2002年11月爆发的SARS疫情作为公共卫生决策模型的模拟应用，对2002年11月1日至2003年7月31日的SARS病例情况进行分析，病例数据见表1。

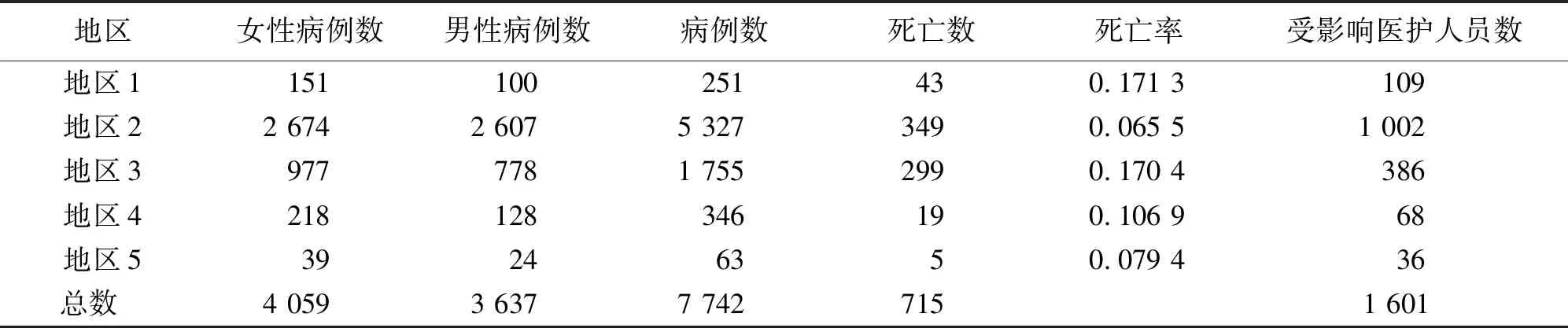
表1 模型应用数据

依照上述数据对4种应急模型进行模拟应用对比。第一步，在结构化预案数据库中搜索匹配应急信息元素，找到应急预案模板；第二步，根据类似案例进行分析计算，确定事件发生地点的周边情况，并根据应急预案模板对事件进行模拟，生成基于模糊相容关系的可视化和优化处理方案；第三步，在结构化预案库中搜索匹配应急信息元素，找到应急响应模板，根据对事件信息的跟踪更新中反映的发展信息要素，不断对可视化处理方案进行评估和调整，指挥人员根据方案下达处理指令。根据事件的后续发展情况对3种决策模型的决策精度进行判断。决策精度的运算如下

(15)

式中，kj表示决策精度，fk表示当前数据决策结论值，hp表示后续数据决策结论值。通过(15)来判断四种模型的决策精度得出模型的优劣。实验将上述数据代入四种决策模型中，并根据不同地区的决策以及划分情况进行分析对比。实验中模型1为本文设计模型、模型2为文献[14]中的模型、模型3为文献[15]中的模型、模型4为传统的Pawlak经典粗糙集建立的模型。

2.2 地区1模型决策实验

依据上述的数据，对地区1使用这些模型分别对公共卫生情况进行应急决策，并得出相应的决策结论，对救援重点给出判断。实验结果见表2。

表2 地区1决策模型决策结论

根据模型中得出的决策结论值，对地区1的事件严重性进行划分，在地区1中，模型3与模型4的决策结论值较高，可达到0.4，划分为严重地区。在地区1的模型应用中模型3精度最低。

2.3 地区2模型决策实验

将地区2中的数据代入4种模型中，并进行应急决策。在实际情况下，该地区受影响最大。实验结果见表3。

表3 地区2决策模型决策结论

地区2情况严重，四种决策模型均将其划分为最严重地区。但四种模型的决策结论值存在区别，需要进一步的实验对比。

2.4 地区3模型决策实验

地区3的实际情况下，受事件影响较为严重，将其数据代入四种模型中得出实验结果见表4。

表4 地区3决策模型决策结论

在表4中，虽然模型1与模型3的决策结论值相同，但划分情况却不同，模型3将地区3与地区2均划入最严重地区，划分存在问题。为了进一步验证应急决策模型的情况，进行进一步的实验。

2.5 地区4模型决策实验

地区4受疫情影响较小，而将地区4的数据代入四种模型中得出实验结果见表5。

表5 地区4决策模型决策结论

在表5中，模型1、2、3对地区4的数值得出的决策结论值相仿，精度均较高，达到67%，为了保证实验结果的可靠性，进行进一步实验。

2.6 地区5模型决策实验

地区5受疫情影响最小，将地区5的数据代入4种模型中得出实验结果见表6。

表6 地区5决策模型决策结论

将地区5的数据代入应急决策模型后，模型1与模型4的决策结论值相同，均将其划分为非严重地区。在五次实验中，模型1的总体决策精度为64.6%、模型2的总体决策精度为53.8%、模型3的总体决策精度为38.6%、模型4的总体决策精度为54%。可证明本文模型在决策精度上最高。

3 结 论

此次设计的公共卫生应急决策模型，通过使用模糊相容关系，提高了模型集合间的相容性，从而提高了模型的决策结论精度。但在设计中使用固定概率向量，容易在应用时影响模糊集的上下近似值。在未来研究中，本文设计的模型需要对固定概率向量进行替换，获得不同决策下损失或收益的概率分布，以提高应急决策模型的可靠性。