基于双弹簧负载倒立摆模型的步态模拟

赵炳炎，陈宗华，刘伟俊

(1.玉林师范学院 物理与电信工程学院，广西 玉林 537000；2.玉林师范学院 体育健康学院，广西 玉林 537000)

0 引 言

1989年Blickha提出了弹簧负载倒立摆模型(spring-loaded inverted pendulum,SLIP)。如图1所示，该模型由一根轻质弹簧和一个质点组成，只需合理设置初始条件和少量参数，就能够模拟人、袋鼠、青蛙等生物的跑跳前进运动[1]。弹簧负载倒立摆模型在前进时只有2个状态(相)，即单腿相和飞行相，所模拟的步态只能在2个相之间切换，可模拟的步态较少[2-5]。

图1 弹簧负载倒立摆模型

双弹簧负载倒立摆模型比SLIP模型多一根弹簧，虽然运动模式更复杂多变，但是可以模拟出更多的步态，且更符合人在体育运动过程中走、跑和跳的规律[6-7]。双弹簧负载倒立摆在前进运动时，可以出现单腿相、飞行相和双腿相，而多出的双腿相意味着更多的步态形式(图2)。

图2 双弹簧负载倒立摆模型

通过建立该模型前进时的动力学方程，并利用MATLAB计算模拟出该模型在不同步态下的稳定前进，不但可以更好理解人在各种步态运动时的生物力学原理，也为研发双足行走机器人提供参考。

1 双弹簧负载倒立摆模型分析

1.1 双弹簧负载倒立摆模型的动力学方程

如图2所示，双弹簧负载倒立摆模型是由一个质量为m的质点连接两根劲度系数为k的轻质弹簧构成，弹簧原长均为l0。只考虑模型前进运动，质点的运动范围限制在矢状面(前进方向和竖直方向构成的平面)内，且机械能守恒。根据运动状态的不同，模型可分为3个阶段：①单腿相，即两根弹簧中只有一根弹簧触地，另一根弹簧在空中摆动；②双腿相，即两根弹簧都触地；③飞行相，即两根弹簧都没有触地，质点在空中只受到重力作用。倒摆在前进的时候，模型会在3个相之间不断切换，切换模式的不同，决定了步态的不同。例如走路步态前进时，单腿相和双腿相的不断切换；跑步步态前进时，单腿相和飞行相的不断切换；跳跃步态前进时，则单腿相、飞行相、双腿相都会出现。弹簧自重忽略不计，所以在未触地时弹簧的摆动对质点的动力学方程没有影响。

在矢状面内建立直角坐标系，令模型前进的方向为x方向，竖直方向为y方向，根据牛顿定律分别建立3个相的动力学方程。单腿相时，系统受到重力和一根触地弹簧的反作用力：

(1)

双腿相时，系统受到重力和两根触地弹簧的反作用力：

(2)

飞行相时，系统只受到重力的作用：

(3)

3个相的动力学方程中，(1)和(2)为非线性常微分方程，无法求得解析解，但可以利用MATLAB中的4、5阶龙格库塔方程函数ode45对动力学方程求数值解。

1.2 各相之间的切换条件

倒摆在前进过程中，模型在3个相之间的不断切换。根据不同步态，将切换规律归纳在表1中。

表1 三种典型步态前进时的相位切换规律

模型处于不同的相，需求解的动力学方程也不同，模型在3个相之间切换，则求解的动力学方程也需在方程(1)～(3)之间切换。所以必须确立相切换的触发条件，当满足触发条件时，则立即终止当前动力学方程的求解，切换到下一个相的动力学方程继续求解。设两根弹簧的支撑点坐标为(0,0)和(x0,0)，倒摆质点的位置坐标为(x,y)。

触发条件①：单腿相→飞行相，此刻触地弹簧正要离开地面与地面压力刚好为零，弹簧保持原长，即

(4)

触发条件②：飞行相→单腿相，此刻质点的高度刚好让一根弹簧触地。α1为单腿触地时与地面的夹角，即

y=l0sinα1

(5)

触发条件③：单腿相→双腿相，此刻悬空的高度可以刚好让另外一根弹簧触地。α2为第二只触地的弹簧与地面的夹角。

y=l0sinα2

(6)

触发条件④：双腿相→单腿相，两根触地弹簧中，其中一根刚好达到弹簧原长。

(7)

触发条件⑤：终止计算，当数值解满足y=0时，质点已经触地，倒立摆倒地不再前进。当vx≤0时，倒立摆向后运动，不再前进。满足上述两种情况，表示运动结束，终止计算。

图3所示的是编程计算的流程图。令倒立摆起始阶段为单腿相，在设定好初始参数后，利用ODE45函数对方程(1)降阶求解。可用ODESET函数的‘Events’选项确定触发条件①～⑤，如果解一旦满足相应的触发条件则立即停止当前相的求解，保存数据并跳入下一个相应相的方程继续求解，初始值由前次已得解确定。接下来的动力学方程求解过程中，继续判断触发条件‘Events’，根据不同的触发事件终止当前相的计算并选择进入下一个相对应的相，继续计算，以此类推，不断切换循环，直到计算时间终止或者所得解满足了触发条件(5)。触发条件(5)表示系统前进失败，停止计算，程序终止。

图3 程序求解流程

3 计算模拟的结果和讨论

模型前进的稳定性严重依赖于模型参数和初始条件的设定。不合理的模型参数或初始条件都会导致倒摆失稳倒地或倒退。我们通过对人在前进运动时的观测，预估出大致的模型参数和初始条件，代入程序后对参数进行大量的调试，模拟出倒摆走路、跑步和跳跃的步态。

3.1 模型参数和初始条件

模型参数设定大致参照成年人体特征，两根弹簧原长为l0=1 m，弹力系数为k=30 kN·m-1，重力加速度为g=9.81 m·s-2，模型质点即质点质量为m=80 kg。初始条件包括质心的起始位置(x,y)，初速度(vx,vy)，弹簧每次触地时的夹角为α1和α2。初始条件(x,y,vx,vy,α1,α2)对前进的稳定性至关重要，需将预估初始条件代入求解程序后，并加以大量的调试得到。这里分别模拟出了双弹簧倒立摆的三种前进步态，走路步态、跑步步态和跳跃步态。将稳定前进时循环计算所得的数值解，利用MATLAB的animation函数动画演示出来，可直观显示出步态，如图4所示。

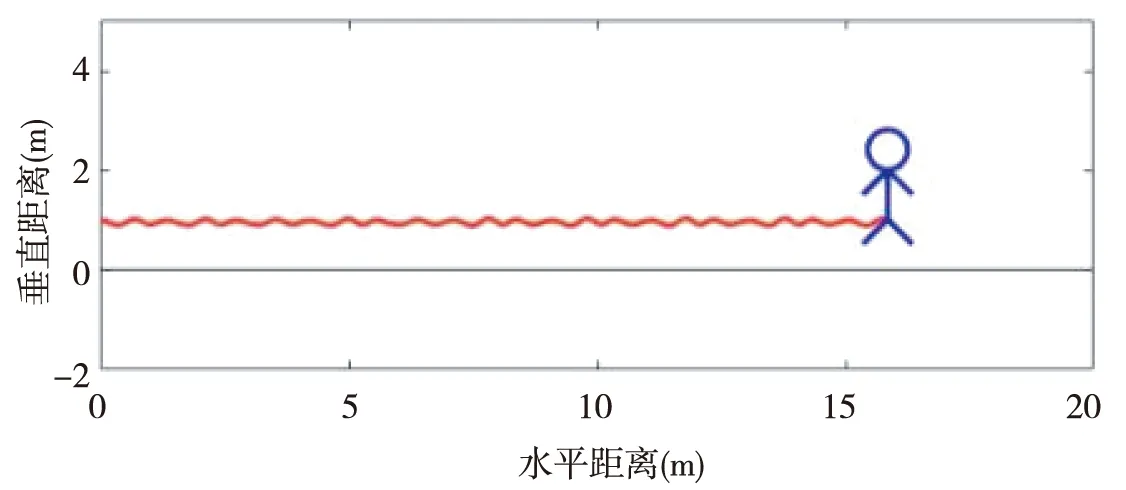
图4 前进时的步态模拟动画

3.2 走路步态

图5 走路步态时质心速度随时间的变化曲线

图6 走路步态时质心高度随前进方向的变化图像

3.3 跑步步态

图7 跑步步态时质心速度随时间变化曲线

图8 跑步步态时质心高度随前进方向的变化图像

3.4 跳跃步态

图9 跳跃步态时质心速度随时间变化曲线

图10 跳跃步态时质心速度随时间变化曲线

4 结论与讨论

1)双弹簧负载倒立摆模型可以模拟出体育运动过程中行走步态、跑步步态和跳跃步态。给出适当范围的模型参数和初始条件，模型可以经过很短时间自动调整出稳定的步态。

2)倒立摆前进步态的稳定性严重依赖于模型参数和初始条件，例如把3.3中的跳跃步态的攻角α1从85.2°微调到83.5°，其他条件不变，则倒立摆只能前进17.7 m就会倒地，导致程序计算终止。因此，合适模型参数和初始条件只能从仿生学角度获得一个大致范围，然后经过大量调试才能获得。

3)对获得稳定步态设定合理的模型参数和初始条件可以考虑利用一些优化算法得到，这也是未来工作方向的重点。