基于重心动力学及虚拟模型的单腿平台运动控制*

谭永营，晁智强，李华莹，韩寿松

（陆军装甲兵学院车辆工程系，北京 100072）

0 引言

单腿平台的运动控制是其实现多步态运动的基础，步行平台所呈现的多种步态可看作各单腿运动的不同组合［1］。不论双腿、四腿还是六腿步行平台，其行走过程中腿部的运动均可归结为摆动和支撑两个阶段，在不同阶段腿部控制的任务不同。在摆动段，腿部运动控制的主要目标是跟踪足端期望轨迹；而在支撑段，腿部运动控制的主要目标是保证机身各自由度期望值的跟踪。在摆动段腿部的运动可等效看作支点固定的多自由度机械臂的摆动，在支撑段腿部的运动可等效看作单腿着地缓冲及恒定高度下施加竖直干扰力两种情况。当腿部各连杆重量较大时，腿部的运动将对机身的运动产生较大影响。而当前在单腿运动控制过程中多仅考虑机身的重量，忽略腿部各连杆重量的影响，无法适用于腿部重量较大的单腿平台运动控制。

单腿平台运动控制最常用的方法之一是基于SLIP（Spring Loaded Inverted Pendulum）的控制方法。Raibert 等在步行平台动步态研究过程中，提出了直腿型及关节型单腿运动控制的SLIP 三分控制方法，成功地将此方法应用于双足步行平台、四足步行平台等的行走控制［2-4］。SLIP 模型是生物学家在步行动物研究过程中，根据动物身体运动规律及腿长变化规律提出的一种简化控制模型，其在单腿平台控制中应用广泛［5-8］。但基于SLIP 的控制方法仅仅抓住了单腿运动的最基本特点，较适合应用于机身重量较大、腿部重量较小的单腿平台。当平台各腿段重量较大时，由于腿部重量的影响，SLIP 控制方法将会产生极大的误差。Pratt 等针对双足步行平台的运动控制，提出了虚拟模型控制算法，但其应用过程中也需要腿部重量较小的假设［9-10］。文献［11-12］将足端空间虚拟模型控制算法应用于单腿平台着地缓冲、连续弹跳等的控制中，取得了较好的效果。文献［13-14］应用关节空间虚拟模型控制算法，实现了步行平台单腿的着地缓冲。当腿部重量较大时，虚拟模型控制算法无法实现对单腿运动的准确控制。

针对上述问题，为实现腿部各杆件重量较大时单腿平台运动的准确控制，在平台的运动学及重心动力学建模基础上，结合重心动力学和虚拟模型控制方法，实现单腿平台的运动控制，并对控制效果进行仿真，验证控制方法的有效性。

1 单腿平台的运动学及动力学建模

单腿平台的模型如图1 所示，包括机身和腿部两部分。单腿平台腿部有3 个自由度，从上到下依次是胯侧摆关节、胯纵摆关节及膝关节，对应的3 个腿段分别为胯侧摆段、大腿段及小腿段。

图1 单腿平台结构

单腿平台结构参数包括腿部各腿段的重量以及腿部各杆件的长度等，如表1 所示。

表1 单腿平台相关参数

2 单腿平台的运动学及重心动力学建模

整个单腿平台的运动与浮基系统类似。因此，运用浮基多体动力学的方法，对单腿平台进行运动学及动力学建模。在此，借鉴Featherstone 提出的空间六维向量对单腿平台各杆件运动学量进行计算［15］。首先对单腿平台的各杆件和关节进行编号，而后建立各杆件的坐标系，如图2 所示。

图2 单腿平台编号及坐标系建立

根据Roberson 与Schwertassek 提出的空间多连杆系统单关节模型，可对相邻连杆的运动学量进行计算，如式（1）所示：

以上各式中，式（3）与式（4）用于计算机身的速度和加速度。式（5）和式（6）中的k=2，3，4，用于计算腿部各杆件的速度和加速度。

由文献［16］可得，单腿平台的速度可由各杆件的速度得到，如式（7）所示：

则单腿平台在六维空间中的关节空间动力学方程可写作以下形式：

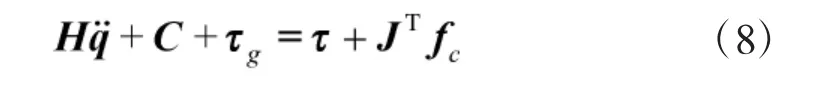
式中，H 为关节空间惯性矩阵，C 为偏差力矩阵，为关节驱动力矩阵，g为各连杆重力矩阵，J 为雅克比矩阵，fc为足端与地面之间的相互作用力矩阵。单腿平台关节空间动力学的H 和C 项可由Featherstone提出的复合刚体算法与逆向动力学算法求得［14］，在此不再赘述。关节1 为假想的虚拟关节，并未施加直接作用力，因此，可将关节空间动力学方程分为机身部分和腿部各连杆部分，如式（9）中所示：

3 基于重心动力学的单腿平台运动控制方法

单腿平台的运动控制本质上是对重心运动的控制。当腿部重量较小时，可仅考虑机身的重量，将单腿平台的重心近似认为在机身的重心处。但在腿部重量较大时，腿部的运动导致平台整体重心的移动。因此，此处采用重心动力学及虚拟模型控制的方式，实现单腿平台的运动控制。

3.1 单腿平台支撑段的运动控制

物体所受合外力等于其质量与加速度的乘积，虚拟模型控制中控制参数易受重量变化的影响，导致无法实现平台的期望运动。在此首先对单腿平台的期望加速度进行计算。由虚拟模型控制可得，单腿平台机身的期望加速度计算如下：

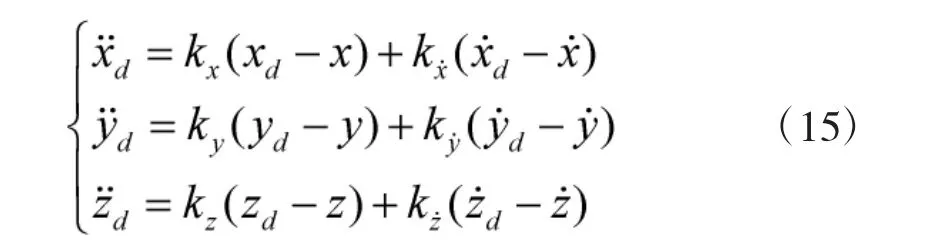
上式中，x¨d、y¨d及z¨d为单腿平台机身的期望加速度。xd、yd及zd为机身的期望位置，x˙d、y˙d及z˙d为机身期望速度，kx、ky、kz及kx˙、ky˙、kz˙分别为各方向相应的位置及速度增益系数。

由于重心动力学控制方法中需要用到单腿平台腿部各关节的加速度，因此，在得到单腿平台期望加速度后，结合雅克比矩阵可得腿部关节的期望加速度如下：

单腿平台重心动力学控制的优点是可以将腿部的重量考虑到控制过程中。因此，结合单腿平台的重心动力学式（12）～式（14）可得，在支撑阶段实现期望运动所需的足端力为：

在得到单腿平台足端与地面接触力后，运用雅克比矩阵，将足端力转换到关节空间，如式（18）所示：

式中，为单腿平台腿部各关节的力矩1，包括胯侧摆关节的力矩2、胯纵摆关节的力矩及膝关节的力矩3。

3.2 单腿平台摆动段的运动控制

在单腿平台运动的过程中，腿部在摆动段相对机身迈出一定距离，以实现支撑点的切换。在摆动段采用虚拟模型的控制方法实现摆动腿的控制，通过虚拟元件的作用使足端沿期望轨迹运动。单腿平台支撑段足端受力计算方法如下：

式中，fsx、fsy、fsz分别为摆动腿足端受力沿1 坐标系各轴的分量，xfd、yfd、zfd及x˙fd、y˙fd、z˙fd为足端在机身坐标系中的期望位置及期望速度，不带下标fd 的变量为各量的实际值，k 为增益系数。

在得到足端受力后，仍然应用雅克比矩阵，将足端受力转换到驱动关节，如式（20）所示：

4 步行平台单腿控制仿真

在步行平台行走过程中，单腿在支撑段的运动，可看作着地缓冲及机身对单腿施加干扰力两种情况，下面分别用文中控制算法及虚拟模型控制算法［17］对单腿平台进行控制仿真，并对控制效果进行对比分析。

4.1 单腿平台运动过程分析

单腿平台的运动主要包括着地缓冲恢复以及竖直干扰两种。此处对单腿在两种情况下的运动进行简单分析，以找到合理的状态机。单腿平台着地缓冲与恢复的过程如图3 所示。单腿平台整个运动过程可分为下落、缓冲及恢复3 个阶段。在单腿平台开始运动后，足端与地面之间接触力fz的有无可作为判断是否开始缓冲的状态机。在足端着地后，缓冲段与恢复段的区别是单腿平台竖直速度v1z的方向，因此，可利用竖直速度v1z的正负来判断恢复阶段开始与否。

图3 运动过程分析

单腿竖直干扰过程包括竖直下压与高度恢复两个阶段，因此，仅通过平台机身竖直速度v1z的正负即可对平台所处的阶段进行判断。

4.2 单腿平台运动控制仿真

为验证重心动力学与虚拟模型控制的有效性，下面运用Adams 与Simulink 对单腿平台竖直干扰及下落缓冲过程进行仿真。在Adams 中建立单腿平台虚拟样机模型（如图4 所示），将控制算法写入Simulink，并建立两者的接口模块。Simulink 中控制算法计算出的力矩施加于Adams 中单腿平台驱动关节处，通过关节的运动实现单腿平台的着地缓冲及抵抗竖直干扰。

图4 Adams 中建立的模型

4.2.1 单腿平台竖直干扰仿真

单腿平台初始时刻以一定姿态站立在地面上，从1 s 开始在机身上施加竖直向下并线性增大的干扰力，在2 s 左右干扰力达到最大值300 N，而后突然撤去干扰力，如图5 中所示。分别用重心动力学及虚拟模型、仅虚拟模型的控制方法，对单腿平台竖直干扰过程进行仿真，并记录平台机身高度的变化。仿真过程中机身的目标高度为0.6 m。图5 中，以VM 表示仅虚拟模型控制时单腿平台相关参数的变化，CG 表示重心动力学及虚拟模型控制时相关参数的变化。

图5 竖直干扰力

由图6 可得，在重心动力学及虚拟模型控制中，未受干扰力时机身竖直高度的误差在-0.013 m～-0.012 m 之间变化，在竖直干扰过程中机身竖直高度误差在-0.044 m～-0.013 m 之间变化；而在虚拟模型控制中，未受干扰力时机身高度的误差在-0.021 m～-0.019 m 之间变化，在竖直干扰的过程中机身高度误差在-0.071 m～-0.019 m 之间变化。因此，与仅虚拟模型控制时相比，重心动力学及虚拟模型的控制方法使机身高度误差减小约37%。单腿平台竖直干扰仿真证明了重心动力学及虚拟模型控制的优越性。

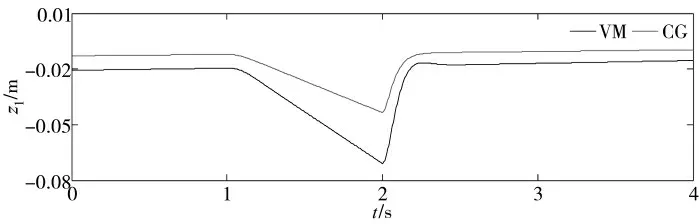
图6 单腿平台高度误差

4.2.2 单腿平台着地缓冲仿真

为实现单腿平台的着地缓冲与恢复，首先参考文献［18］中的方法，规划单腿平台机身的轨迹。采用恒加速度的缓冲方式对单腿平台着地过程进行规划，实现一定距离内平台速度的缓冲。在恢复阶段，由于初始及结束时的加速度、速度与位置均为已知量，因此，采用5 次曲线对恢复阶段进行规划。假设tc1与tc2分别为缓冲过程及恢复过程所用时间，则单腿平台的轨迹如式（21）所示：

式中，h1、h2及h3分别为平台缓冲相初始、缓冲结束时及恢复过程结束时机身的高度，v1为缓冲相初始机身的速度，a1为缓冲相初始的加速度。假设单腿平台下落高度为0.1 m，h1、h2、h3分别为0.6 m、0.53 m、0.6 m，tc1为0.1 s，均tc2为0.2 s，则单腿平台机身的轨迹如图7 所示。

图7 机身轨迹

分别用重心动力学及虚拟模型、仅虚拟模型的控制方法，使单腿平台的机身跟踪期望轨迹，并记录相关参数的变化，如图8～图9 所示。

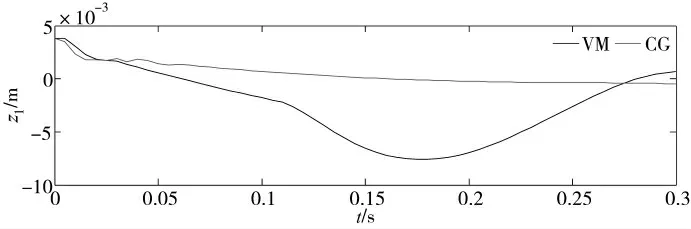
图8 机身高度误差

图9 机身速度误差

由图8～图9 可得，两种控制方法均能实现单腿平台的着地缓冲，但控制效果有较大差异。由图8可得，在重心动力学及虚拟模型控制中，机身高度误差的绝对值保持在0～0.004 m 范围内，而在仅虚拟模型控制中机身高度误差在0～0.008 m 范围内，且平台高度出现较大波动。因此，与虚拟模型控制时相比，重心动力学及虚拟模型控制方法使高度跟踪误差减小约50%。由图9 可得，在重心动力学及虚拟模型控制中，单腿平台竖直速度跟踪误差的绝对值在0～0.001 6 m/s 范围内变化，并且竖直速度跟踪误差波动较小；而在仅虚拟模型控制中，竖直速度跟踪误差的绝对值在0～0.2 m/s 范围内变化，且速度跟踪误差的波动较大。单腿平台着地缓冲仿真结果进一步证明了重心动力学及虚拟模型控制的有效性及优越性。

5 结论

本文针对腿部重量较大的单腿平台，提出一种基于重心动力学及虚拟模型的控制方法，并运用动力学仿真验证了控制方法的有效性。得到的结论如下：

1）重心动力学及虚拟模型的控制方法，既保留了虚拟模型控制实现简单的优点，又能依靠重心动力学提高单腿平台位置及速度的跟踪精度；

2）重心动力学及虚拟模型控制方法，能够减小单腿平台位置及速度跟踪时的波动；

3）重心动力学及虚拟模型控制方法，通过重心动力学实现了对较大腿部重量的适应性。