基于时序打击的空地弹药消耗预测模型

李建华，于洪敏，张雪胭，王申坪，董 薇，杨晔楠

（国防大学联合勤务学院，北京 100858）

0 引言

现代战争中，为了快速达成作战目的、尽量减少进攻伤亡，通常组织大规模空袭行动用以摧毁敌方地面重要目标和有生力量，这使得空地弹药消耗量不断增加。为了实现以最小损耗代价获得最大毁伤效果，需要构建科学合理的空地弹药运用方法，弹药消耗预测结果不仅可以确定弹药的数量和比例，还可确定飞机、弹药、目标的分配方案，为制定作战方案和保障方案提供重要依据。由于飞机、弹药、目标种类繁多，会产生大量飞机-弹药-目标分配方案，导致弹药消耗结果呈现不确定性。火力分配（Weapon-Target Assignment，WTA）是一种预测弹药消耗量的有效途径，可根据敌我双方交战态势、作战意图及目标、武器参数，在约束条件限制下，以毁伤敌方目标价值最大或武器弹药损耗最小等为目标函数，求解武器-目标最优分配。运用火力分配方法预测弹药消耗量，需重点研究以下4 个方面问题：一是确定弹药性能，即弹药对目标的毁伤效果；二是确定最优分配，即武器-弹药-目标的最优组合；三是确定各种因素的影响，例如目标修复、武器损失、弹药消耗、天气条件等因素影响；四是加入时间要素，即能够正确反映作战过程。

自1995 年起，美国空军就使用火力分配方法预测空地弹药消耗量，主要包括HEAVY ATTACK模型、THEATER ATTACK 模型和MIXMASTER 模型。HEAVY ATTACK 模型估计每个目标的价值，通过求解毁伤目标的总价值预测弹药消耗量，该模型计算速度快，但约束条件少，不能模拟飞机损失［1］；THEATER ATTACK 模型按飞机、弹药、目标、距离、天气状况和作战阶段等条件分配架次，使用的目标函数与HEAVY ATTACK 模型相同，但该模型为全局优化模型，数据量非常大，计算时间较长［2］；MIXMASTER 模型使用目标价值确定每个目标类型的可用架次数，运用启发式算法计算毁伤目标的总价值，但该模型未考虑作战时间的影响［3］。

目前，我国火力分配研究在分配模型假设、目标函数选择、约束条件设置和优化算法运用等方面研究较为深入。模型假设是交战过程的数学抽象，直接决定了模型的合理性，文献［4］按对抗方式将WTA 分为直接对抗式WTA 与间接对抗式WTA，按时间要素将WTA 分为静态WTA 与动态WTA，文献［5］又根据目标威胁，将WTA 分为狭义WTA 和广义WTA。目标函数是作战意图的直接体现，主要以目标价值最大［6］、资源损耗最小［7］或武器损失最少［8］等为准则，但目标函数的构建还不够合理，以毁伤目标价值最大为例，存在实际作战中难以确定目标价值的问题。约束条件规定了问题的求解限制，决定了问题的复杂程度，主要与武器弹药数量、准备时间、作战意图等相关，文献［9］在这方面进行了有益探索，提出了基于随机组合的约束条件设置方法。优化算法是求解问题的主要手段，传统方法包括分枝定界法［10］、隐枚举法［11］和动态规划法［12］等，但传统算法存在难以处理大规模WTA 的问题，随着计算机技术的发展，遗传算法［13］、粒子群算法［14］和蚁群算法［15］等智能算法被广泛用于求解WTA 问题。

实际作战中，目标修复、武器损耗、天气条件和目标毁伤效果评估等因素均可能对弹药消耗造成较大影响。科索沃战争中，由于目标毁伤效果评估能力不强，美军平均每天至少有40 次重复打击，消耗了大量弹药。而且这些因素随时间不断变化，若不考虑时间要素对弹药消耗的影响，往往不能正确反映作战过程。因此，本文在火力分配算法基础上，根据空地弹药的运用特点，建立了基于时序打击的飞机-弹药-目标的分配模型，提出了架次损失、目标修复和目标毁伤效果评估对弹药消耗影响的计算方法，以目标集合阶段指标完成度、架次数和弹药消耗量为目标函数，设置飞机损失、弹药储备等多种约束条件，计算空地弹药消耗量。本文方法可为空地弹药作战运用和弹药保障方案的制定，提供理论参考依据和方法支撑。

1 弹药消耗预测模型的构建

空地弹药消耗预测模型以作战任务为牵引，以打击时序为主线，综合考虑天气条件、目标毁伤效果评估和目标修复等因素影响，用目标集合阶段指标完成度、架次数和弹药消耗量的最小值为目标函数，设置弹药储备、可用架次和飞机最大损失等约束条件，求解最优飞机-弹药-目标组合下弹药消耗量。空地弹药消耗预测模型的建立主要包括以下内容：

1）作战阶段和目标集合的划分，以及目标集合阶段指标的设定；

2）飞机-弹药-目标火力分配模型的建立；

3）飞机可用架次数的计算；

4）影响因素的计算。

1.1 作战阶段和目标集合划分

由于模型中的飞机数量、弹药数量、架次率、阶段指标、目标修复率等数值随时间变化，因此，需要考虑时间要素。为此将整个作战过程划分为若干个阶段，按时间顺序打击目标。时间因素的加入会极大增加计算复杂度，为了简化计算，规定作战过程由整数个阶段组成，每个阶段由整数个固定长度的周期组成。阶段长度可以不相等，但周期必须相等，作战阶段划分示例如图1 所示。

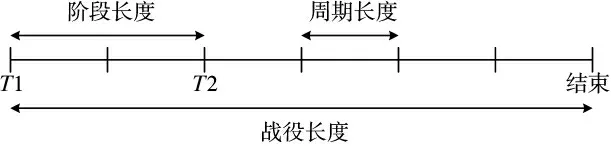
图1 战役长度、阶段长度和周期长度

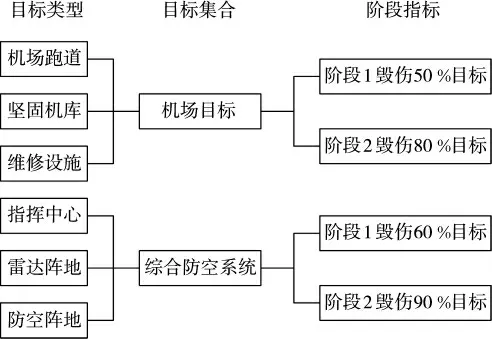
图2 目标、目标集合和阶段作战指标

1.2 火力分配模型

其中，fket为惩罚函数，δket为实际毁伤指标与规定毁伤指标的差值，α、β、γ 为系数，sit表示阶段内可用架次数，Lossit为阶段内飞机的最大可损失数。

惩罚函数可以是具体数值也可以是函数，本文给出一种惩罚函数的定义方法：

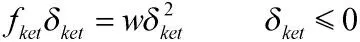
其中，w 为正数。

1.3 可用架次数的计算

为了计算任一种飞机在一个阶段内的架次数，定义架次数是架次率（用h 表示）、损失率（用l 表示）和时长（用t 表示）的函数，st为单架飞机在t 时数量，则：

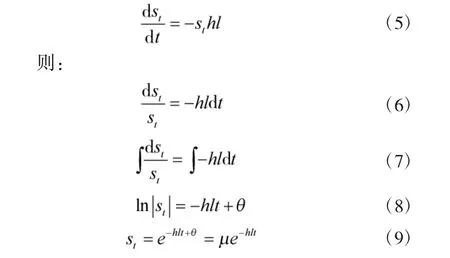
当t=0，单机飞机架次数为1，即μ=1，乘以h 即为单架飞机架次数，则在时间t 内架次数为：

架次数包括可用架次数和不可用架次数，其中不可用架次数是因受到天气条件、弹药消耗和飞机损失的限制，其中弹药消耗和飞机损失作为约束条件，定义了天气条件对架次数的影响。

为了确定天气条件带来的影响，定义天气条件与可用架次概率的对应关系，如表1 所示。

表1 天气条件与可用架次概率的对应关系

假设天气状况为W3 或者更好，那么该飞机的实际可用架次数等于架次数乘以0.85。不考虑当飞机到达目标时由于天气影响无法投弹的情况。

2 目标修复和目标毁伤效果评估的影响

使用空地弹药打击目标后，目标可能处于多种状态，为了明确目标遭受打击后的状态，定义目标状态的5 种情况：

未毁伤：未击中目标；毁伤：击中目标，目标可修复；报废：目标被彻底摧毁；修复中：目标处于修复状态；修竣：目标修复完成。

为了减少计算的复杂度，作如下假设：

1）每种类型目标的可修复概率和修竣概率是固定值，与目标数量和损毁数量无关；

2）确认目标处于报废或修竣状态需要一个周期；

3）在每个阶段打击目标的数量是固定值，而且平均分配到每个周期；

4）目标毁伤效果评估结果正确或错误的概率是固定值，如果目标毁伤效果评估结果错误，则在下一个周期再次打击目标，再次打击后目标的状态即被确认；

为了计算目标每个阶段目标的修复数和报废数，定义以下变量：

T0为阶段开始时刻；T1为阶段结束时刻；c 为周期长度；m 为周期数量；Li为周期i 开始时未毁伤的目标数量；L0为阶段初始未毁伤的目标数量；Ri为周期i 开始时修复中的目标数量；R0为阶段初始修复中的目标数量；Di为周期i 开始时报废的目标数量；D0为阶段初始报废的目标数量；K 阶段内打击的目标数量；Ki周期i 内打击的目标数量；K0上一阶段最后一个周期打击的目标数量；Pr为目标修复概率；Pnr为目标不可修复概率，Pnr=1-Pr；Pc为目标下一个周期修竣的概率；Pnc为目标下一个周期不能修竣的概率，Pnc=1-Pc；Pb为目标毁伤评估结果正确的概率；Pnb为目标毁伤评估结果错误的概率，Pnb=1-Pb；r 目标修复速率。

为了控制目标修复数量，可以通过输入修复概率Pc来确定每个周期后修复的目标的预期数量。为了计算Pc值，定义X 为维修时间函数：

修复中目标数量与报废目标数量的计算方法相似。

第i 个周期维修中的目标数量为：

打击未毁伤目标导致处于维修中的目标数量为：

如果模型安排足够数量的打击，即K 足够大，就可使该阶段结束时未毁伤的目标数量为0，规定Lm=0 时，打击目标数量的最大值用Kmax表示。

为了说明Kmax，设定以下条件，作战阶段为30 d，每个周期c=3，R0=0，L0=100，Pb=1.0，即：

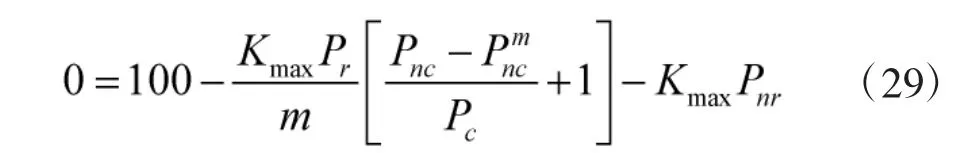
则：

根据式（12）和式（29），可求得打击目标数量最大值Kmax与修复速率r、修复概率Pr的关系，如图3所示。

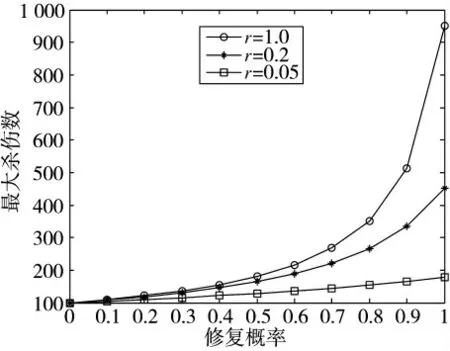
图3 最大杀伤数和修复速率和修复概率的关系

为了说明阶段结束时修复中的目标数量，设定以下条件：作战阶段为30 d，每个周期c=3，R0=0，K=100，Pb=1.0，则：

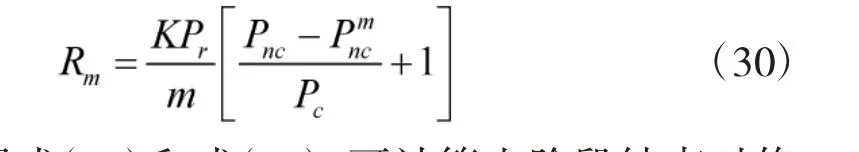
根据式（12）和式（30），可计算出阶段结束时修复中的目标数量Rm与修复速率r、修复概率Pr的关系，如图4 所示。

图4 阶段结束时维修中的目标数量

3 算例分析

为了验证模型的可行性和有效性，编写了算例（算例中数据均为假设值）。

假设战役分为两个阶段，第1 阶段4 个周期，第2 个阶段6 个周期，每个周期3 d，我方有6 种飞机，8 种弹药，敌方目标有4 种，我方飞机和弹药第1、2 阶段的参数相同，具体数据如表2～表4 所示，其他参数不再一一列出。

表2 敌方目标参数

表3 我方弹药参数

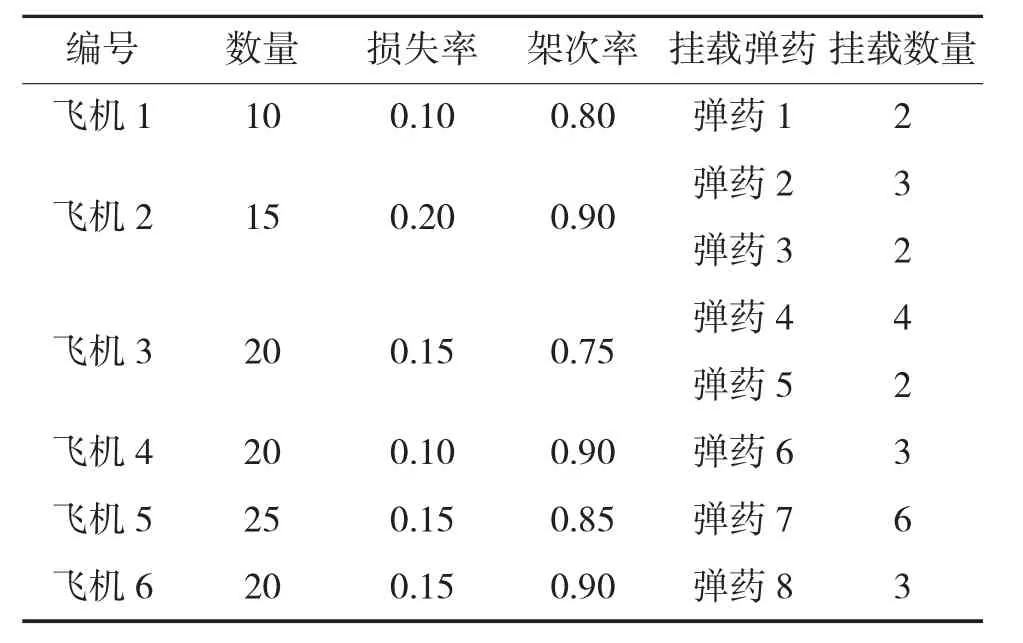
表4 我方飞机参数

使用LINGO 软件对上述算例进行了求解，每个阶段的弹药消耗预测结果如下页表5、表6 所示。

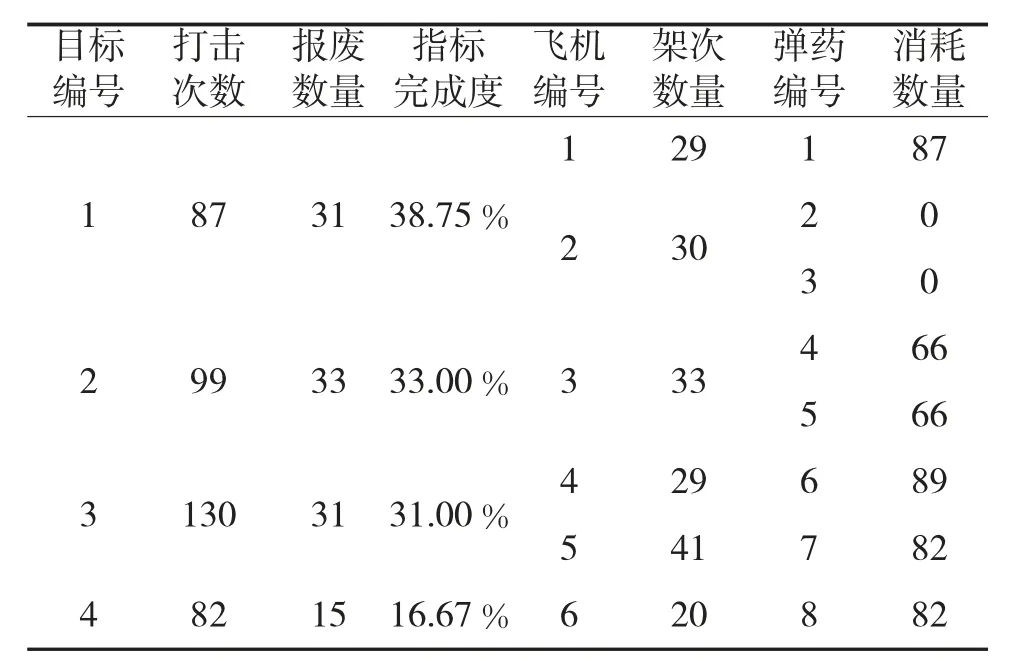
表5 第1 阶段计算结果

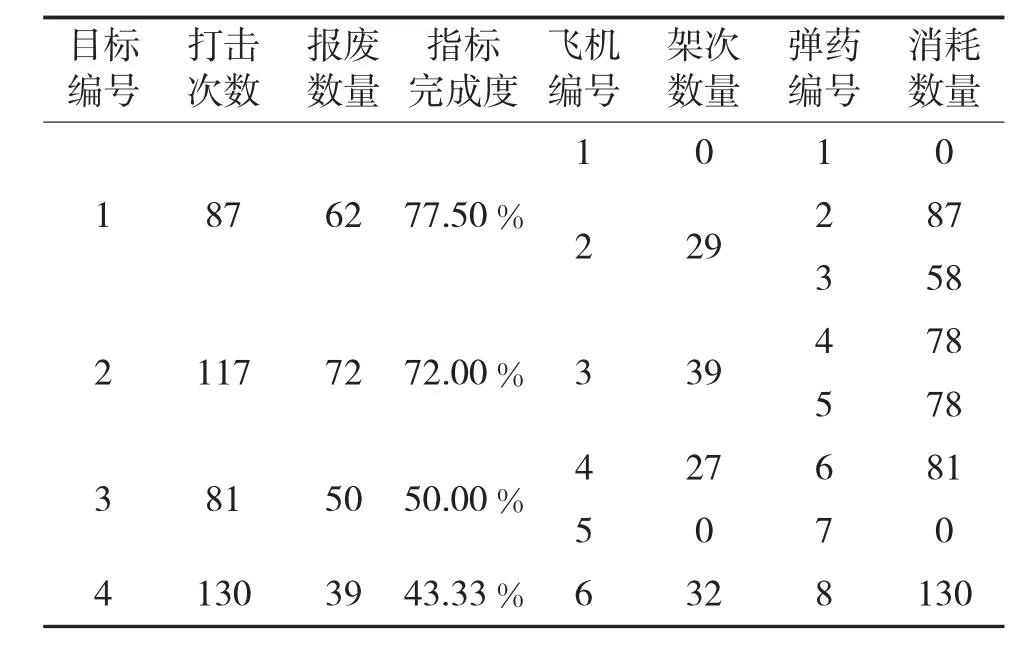
表6 第2 阶段计算结果

由表5 和表6 可以看出：

1）目标1 和目标2 的阶段指标完成度较高。由于为目标集合1 设置了较大的惩罚函数，在弹药储备、可用架次和飞机损失的限制下，优先完成目标1和目标2 的打击任务；

2）打击次数大于报废数量。由于考虑了目标毁伤效果评估和目标修复等因素带来的影响，导致较多的重复打击，符合作战实际。

4 结论

本文建立的基于时序打击的空地弹药消耗预测模型，以任务指标为目标函数，综合考虑多种影响因素和约束条件，计算了空地弹药消耗量，并给出了飞机-弹药-目标分配方案，较为符合作战实际，可为作战计划和弹药保障计划的制定实施提供理论依据和方法支撑。空地弹药消耗预测是一项复杂工程，需继续加强以下3 个方面的研究：一是预测模型与作战使命相关联，区分单一作战和联合作战；二是拓展影响因素的研究范畴，例如敌方防空体系、目标伪装情况等；三是提高弹药对目标命中概率计算方法的精确性。