例谈数学核心素养培育问题

佛山市顺德区第一中学(528300)关嘉欣

2017年,新版普通高中数学课程标准明确提出数学六大核心素养:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.数学学科核心素养的确立让数学教学回归学科本质,强调学科的独特育人价值.

在新高考、新课标、新教材的背景下,我们都知道数学核心素养的重要性,但到底如何在课堂教学中培育学生核心素养呢?其实,为了落实数学核心素养的培育,我们需要找到核心素养与具体的课程内容(包括知识与方法)的内在关联,在知识讲授的过程中有意识地有针对性地渗透.下面我想以必修一第三章第2 节“函数的单调性与最(小)值”为例谈谈如何在课堂教学中落实数学核心素养.

“函数的单调性与最(小)值”这节课要求学生能准确用符号语言刻画函数的单调性与最值、利用函数单调性的定义证明具体函数的单调性、把现实问题抽象为数学模型,并能利用函数单调性与最值的知识来解决.因此,这节课是很好地渗透数学核心素养的载体.下面从教学过程的5 个方面来展开阐述.

1 感知概念,渗透数学抽象的核心素养

(1)思考这两张新冠肺炎疫情数据关系图呈现了什么信息?

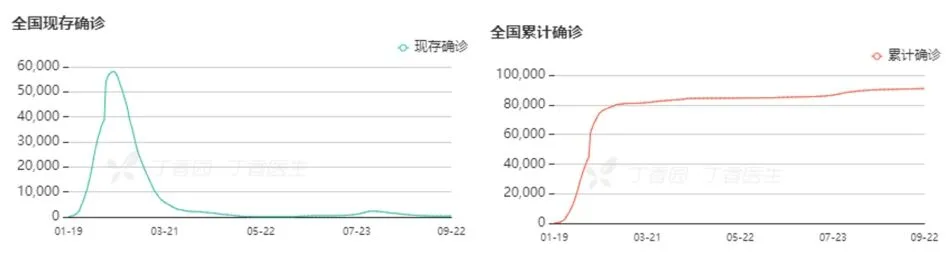
图1

预设 随时间的推移,全国现存确诊人数先上升后下降;全国累计确诊人数一直上升,前面升得比较快,后面升得比较慢.两张图都反映了函数图象的变化情况.

(2)分析下列熟悉的函数图象,你发现了什么共同性质?

图2

预设 上述函数图象都有函数值随自变量的增大而增大(或减小)的性质:函数的单调性.

设计意图①从真实情境:新冠肺炎疫情图出发,理解函数单调性的现实意义,感受数学与生活的密切联系,能从情境中抽象出数学概念,积累从具体到抽象的活动经验,养成在日常生活和实践中一般性思考问题的习惯;

②从学生熟悉的函数图象入手,这当中有递增的,也有递减的,也有增减变化的,通过丰富的实例让学生对函数单调性的概念有初步直观感性认识,运用数学抽象的思维方式思考并解决问题.

2 探究概念,渗透直观想象、逻辑推理的核心素养

2.1 用图象语言刻画单调性,渗透直观想象的核心素养

(1)观察你们熟悉的一次函数、二次函数图象,分析它们的单调性.

图3

预设学生分析结果

①左图从左到右,图象上升→y随着x的增大而增大→单调递增.

②中间图从左到右,图象下降→y随着x的增大而减小→单调递减.

(2)观察右图,如何刻画它的单调性?说明函数的单调性是一个整体性质还是一个局部性质?

③右图在(−∞,0]单调递减;在[0,+∞)单调递增,说明函数的单调性是一个局部性质.

(3)思考 用图象来判断单调性万能吗?如果不是,可能会有什么问题?

预设 可能存在的问题:①图象不够严谨,眼见不一定为实.②如果函数画不出图象,那就判断不了单调性.因此,我们需要从图象语言过渡到符号语言.

设计意图 ①从学生熟悉的函数入手,借助几何直观理解问题,形成数学直观,在具体的情境中感悟事物的本质,渗透直观想象的核心素养;②引发冲突,指出函数单调性是一个局部性质;③通过讨论用图象判断函数单调性的局限性,引发学习符号语言刻画单调性的动机.

2.2 用符号语言刻画单调性,渗透逻辑推理的核心素养

(1)如何用符号语言刻画函数y=f(x)在区间D上单调递增?

把“在区间D上,函数值随着自变量的增大而增大”这句话翻译成符号语言.

①自变量的增大:x1

②函数值随之而增大:f(x1)

(2)问题集中在自变量,需要回答:

①自变量在哪里取值?(x1,x2∈D)

②自变量如何取值?(需要进一步探究)

(3)如何取x1

①如果1,3∈D,f(1)

②在D上取无数多个点x1

图4

图5

分析 ①②无法确保的原因是都有可能∃x1,x0∈D,虽然x1f(x0),因此,需要对∃x1,x0∈D进行否定,而对存在量词的否定就是全称量词,因此只需要把∃x1,x0∈D改为∀x1,x0∈D.

设计意图 ①分析过程从特殊到一般进行推理,能用数学语言有逻辑地表达与交流,渗透了逻辑推理的核心素养;

②“任取x1,x2”对学生而言是难点,需要重点突破.为了解决这个难点,通过反例引发冲突与思考,加深对任意性的理解.结合第一章关于全称量词与特称量词的学习,学生能说出特称量词的否定是全称量词.

3 建构概念,渗透数学建模的核心素养

(1)经过上述讨论,请你尝试用符号语言给出函数f(x)在区间D上单调递增的定义.

预设 一般地,设函数f(x)的定义域为I,区间D ⊆I,如果∀x1,x2∈D,当x1

图6

图7

对学生给出的定义进行整理补充,并重点剖析概念:

①局部性:指明函数单调性发生在哪个区间;

②任意性:x1,x2的取值是任意的;

③同号性:x1,x2与f(x1),f(x2)的符号保持一致性.因此,也可用(x1−x2)(f(x1)−f(x2))>0 与来刻画.

(2)类似地,请你给出函数单调递减的定义.

预设 一般地,设函数f(x)的定义域为I,区间D ⊆I,如果∀x1,x2∈D,当x1f(x2),那么就称f(x)在区间D上单调递减.特别地,如果f(x)在它的定义域上单调递减时,我们就称它为减函数.

设计意图①让学生自主归纳建构概念,培养学生抓住本质准确表达的能力,提高学生用数学的语言表达问题、用数学方法构建模型解决问题的素养,从而渗透数学建模的核心素养;

②让学生学会使用类比给出相似概念,体会类比这一数学方法.

4 辨析概念,渗透直观想象的核心素养

例1根据单调性的定义,完成概念辨析:

(1)若f(2)

(2)f(x)在[2,3]上单调递增,则f(2)

(4)若f(x)单调递增,若f(a)

例2判断课本P73 题目7、13 这三个函数的单调性:

(1)G(n)=3n+1,n ∈{1,2,3}.

(3)f(x)=[x],x ∈(−2.5,3].

结合图象分析.

图8

总结

设计意图从具体函数入手,借助几何直观理解问题,形成数学直观,在具体的情境中感悟事物的本质,渗透直观想象的核心素养,理解函数单调性的概念.

5 应用概念,渗透逻辑推理、数学运算的核心素养

例3根据定义,研究函数f(x)=kx+b(k ̸=0)的单调性.

例4物理学中的玻意耳定律(k为正常数)告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大.试对此用函数的单调性证明.

例5根据定义证明函数在区间(1,+∞)上单调递增

小结用定义法证明函数单调性的一般步骤:

(1)取值:在区间D上,任取x1,x2,令x1

(2)作差:求f(x1)−f(x2);

(3)化简:因式分解,变形为因式相乘除的形式;

(4)定号:确定f(x1)−f(x2)的正负;

(5)下结论:根据“同增异减”原则,指出函数在区间上的单调性.

设计意图通过证明函数的单调性,加深对定义的理解,掌握代数式作差、通分、因式分解的运算法则,探究运算思路,设计运算程序,从而培养逻辑推理与数学运算的核心素养.

数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现.但这种素养的获得并不是凭空产生,它依托于数学学习过程与真实情境.

因此,我们要在教学设计上多下功夫,在日常的教学与课堂中,以具体数学知识为载体,以数学方法与思想为工具,渗透数学核心素养.只有这样,数学核心素养才不会成为无源之水,纸上之言,才能真正落到实处,帮助到学生.