空间大型结构体组装接口设计及装配性能分析

史 创，郭宏伟，王洪洋，陶 磊，刘荣强，邓宗全

(哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨 150001)

0 引 言

现如今，无论是太阳能电站还是空间反射镜等结构体的尺寸和质量都越来越大，而且其支撑机构也很大[1]。但是现在以及未来一段时间内，运载工具还很难将整个大型结构体运送到太空中，只能分批运送，在空间中组装[2]。在轨组装技术的运用大大扩展了空间作业范围。

美国宇航局曾提出利用在轨组装技术将多个聚光镜组装成太阳能电站[3]。西北工业大学的黄攀峰等人提出了细胞卫星的概念,将卫星的各部件拆开，在空间轨道中组装[4]。在20世纪90年代，为了实现在空间中完成桁架结构的装配，NASA开始研究一套装配系统，主要设计思想是使用机器人远程遥控完成装配。对机器人进行路径的规划，当机器人到达指定位置后提供输入力矩进行装配[5]。

无论是航天器还是空间轨道运行等，空间对接都是必不可少的[6]，对接接口则是其中关键的结构。无论是在国内还是国外，学者们都创造了许多不同的空间对接接口形式。例如，为了实现“spheres”模块的对接，美国提出了一种不同于机械对接接口的形式，该接口主要采用电和磁结合的方式[7-11]。其主要原理是电生磁，将线圈和接口相连，接口在磁力的作用下相互靠近实现对接。考虑到对接时会产生冲击，所以还设置了偏置弹簧提高对接的稳定性。对于阿波罗与联盟号之间的对接，美苏两国设计了周边式对接机构。机构主要分为主动和被动两部分，将捕捉环和主动部分的可移动杆件连接起来，杆件带动环运动，同时机构还设有缓冲机构，通过捕捉环的运动以及缓冲机构的缓冲来实现机构的平稳对接[12]。在1996年，日本设计的一种接口具有末端执行机构，该机构有钩爪用于抓取装置，并且为了实现锁定还设置有锁紧机构[13-14]。美国曾在航天器上采用了“锥—杆”式对接机构，还设有独立的锁紧机构，均布在圆周上完成对机构的锁紧，该对接机构具有良好的密封性[15]。由DARPA提出的轨道快车项目中使用的对接机构为三爪式，主要作用是捕捉被动部分，随后四连杆机构在电机的带动下开始运动。最终，在一系列的动作后,锁紧手爪的锁紧与对接[16-18]便可完成。上海宇航工程系统研究所的张华研究了对接机构的锁紧，得出了通过减小摩擦力可提高对接锁系运动的同步性的结论[19]。哈尔滨工业大学的史士财等设计了空间机械臂的快换接口，该接口采用了双圆锥面的配合方式[20]，拆卸方便。在2017年，中北大学创造了一种新型在轨模块对接接口。该接口的形式采用三爪式，并将自适应技术和记忆合金技术融入其中[21]。

结合以上内容可知，目前所设计的对接接口多采用电磁或电动结构实现对接和锁紧，且大多为单次锁紧，可靠性欠佳。机器人技术越来越先进，空间大型乃至超大型结构体的建立将越来越依赖在轨组装技术。

本文以实现空间大型结构体的在轨组装为重要出发点，设计了全新的组装接口。论文章节安排如下所示:论文第1节提出并设计了一种全新的空间对接机构;第2节针对对接接口，具体的分析了其容差性能;论文第3节通过仿真分析，研究了组装接口对接参数对对接过程的影响规律。

1 组装接口

1.1 原理设计

为了提高在轨组装的容差性能和对接过程的稳定性，本文设计了锁紧爪式对接机构，如图1所示,为机构的原理图。

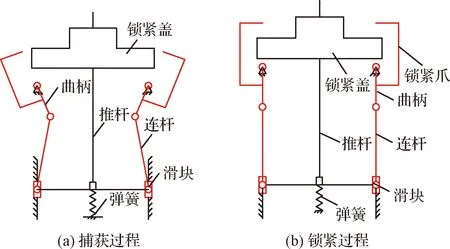
图1 对接机构原理图Fig.1 Schematic diagram of the docking mechanism

弹簧压缩后为机构的运动提供动力，为提高锁紧机构的可靠性，采用三爪式和钢球式机构联合锁紧。对接接口可分为两个部分：导向机构与锁紧机构。

1.2 导向机构

导向机构的组成部分有推杆、压缩弹簧、螺纹盖等。图2(a)为机构剖面，图2(b)为三维模型。导向头的头部结构为锥形，角度是45°，在导向头上开了八个槽，用于装载钢球。为提高锁紧盖与推杆、导向头与螺纹端盖之间连接的稳定性，采用的连接方式为螺纹连接。在对接过程中，组装单元受到机械臂的推力，导向头开始运动并靠近上箱体，当其到达预先设置的限位位置时，由于推力变大，用于减轻对接过程产生的碰撞的压缩弹簧开始压缩，推杆开始运动到锁紧为止。

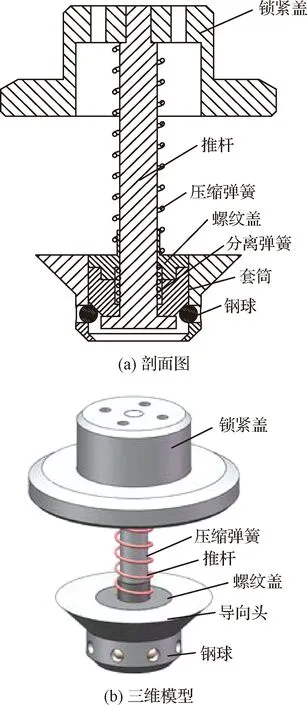
图2 导向机构Fig.2 Guide mechanism

1.3 锁紧机构

导向头和锁紧盖的锁紧依靠锁紧机构来实现，空间结构组装单元的对接在锁紧动作结束后便完成了。锁紧机构的驱动力由受到推杆推动的导向件提供，主要由上箱体、锁紧爪、曲柄、连杆、驱动弹簧、导向件以及相应的轴和配件组成。在上箱体设置了限位结构，从而可以准确的锁紧以120°的间隔均匀分布在其上的锁紧爪。锁紧爪的运动伴随着冲击的产生，驱动弹簧可以缓冲此过程的冲击。导向件相当于曲柄滑块机构中的滑块，可带动该机构进行运动，最终完成锁紧。具体结构如图3所示。

图3 锁紧机构Fig.3 Locking mechanism

主动件是驱动曲柄滑块机构转动的导向件，导向件运动带动曲柄运动。当曲柄转动到如图4所示的位置时，曲柄滑块机构的主动件和从动件共线，到达死点位置，这样便可实现自锁，从而锁紧锁紧盖。

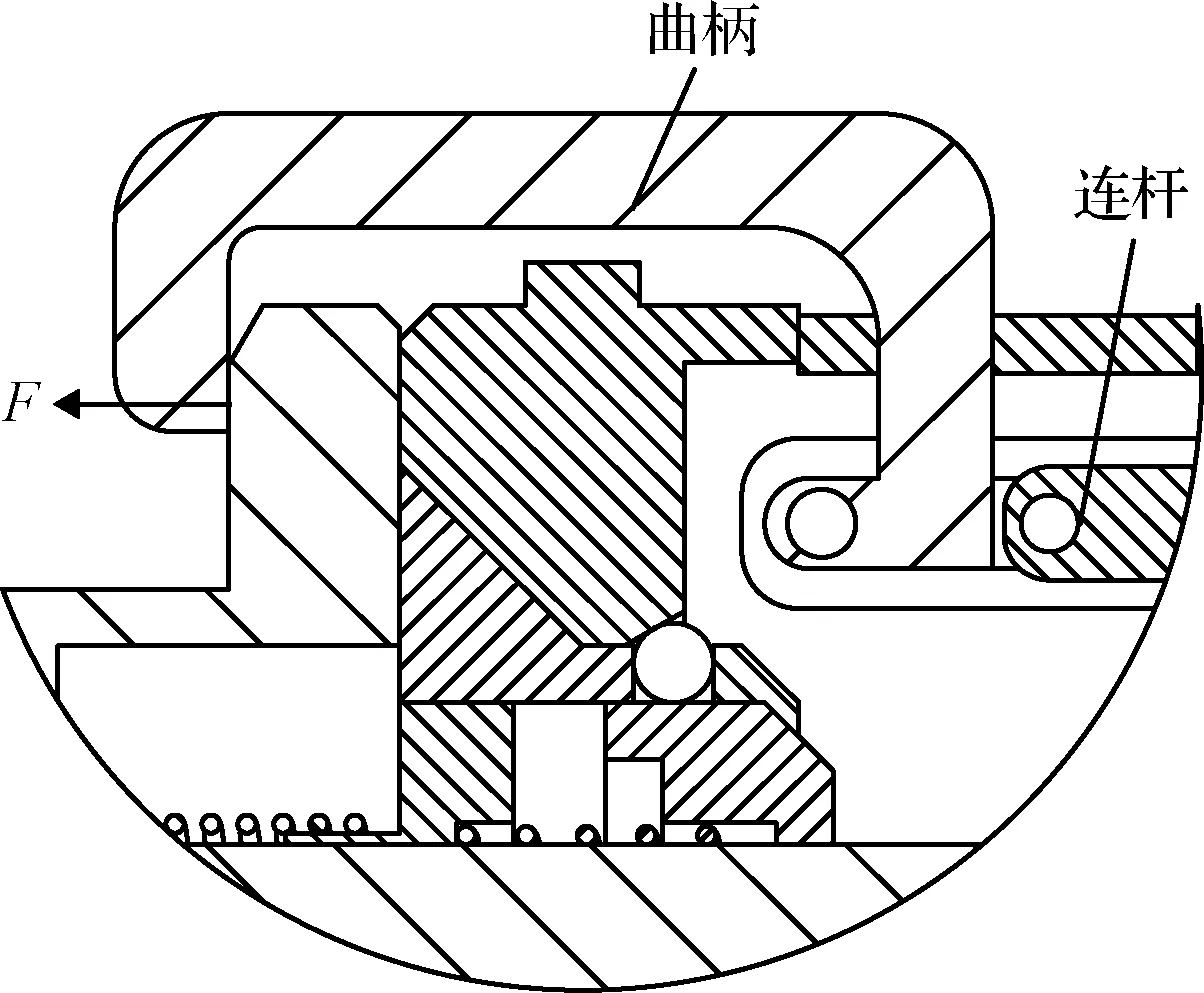
图4 死点位置Fig.4 Dead-center position

本文使用了双重锁紧，可以较大程度将空间结构组装单元在轨对接的连接刚度提高。导向头和上箱体的锥形内壁接触并继续运动，在其到达指定的位置后，机械臂提供更大的推力，推杆的受力平衡遭到破坏而向下运动，螺纹盖和分离套筒在分离弹簧的作用下开始产生相对运动、逐渐分离。分离套筒在运动过程中对钢球施加压力，当压力达到一定值时,钢球开始运动。钢球向上箱体开的凹槽运动，最终在这两个槽内各占据自身体积一半的位置，导向头的锁紧完成，此方案有效的提高了对接接口的可靠性。

1.4 对接运动过程

整个对接过程如图5所示。

如图6所示，第一阶段，由于重叠现象的出现，接口会产生位姿偏差。需要同时调整自身位姿及相互之间的相对位置。

第二阶段，导向头触碰到锁紧机构的上箱体，在进入上箱体的对接锥形结构后，继续运动直至完全进入，其运动到位后的状态如图7所示。在此过程中产生的碰撞可以通过导向结构的压缩弹簧减轻。

第三阶段，由于上箱体锥形内壁的限制，导向头停止运动。锁紧盖和推杆继续运动，推动分离套筒运动并挤压钢球，实现如图8所示的钢球锁紧。

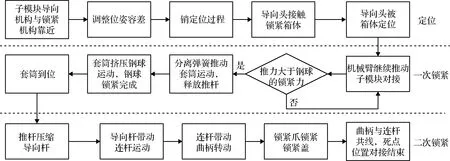
图5 组装过程Fig.5 Assembly process

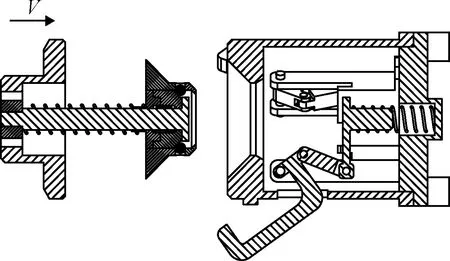
图6 位姿调整Fig.6 Pose adjustment

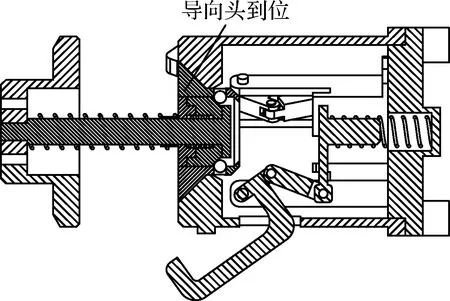
图7 导向头到位Fig.7 Guide head in place

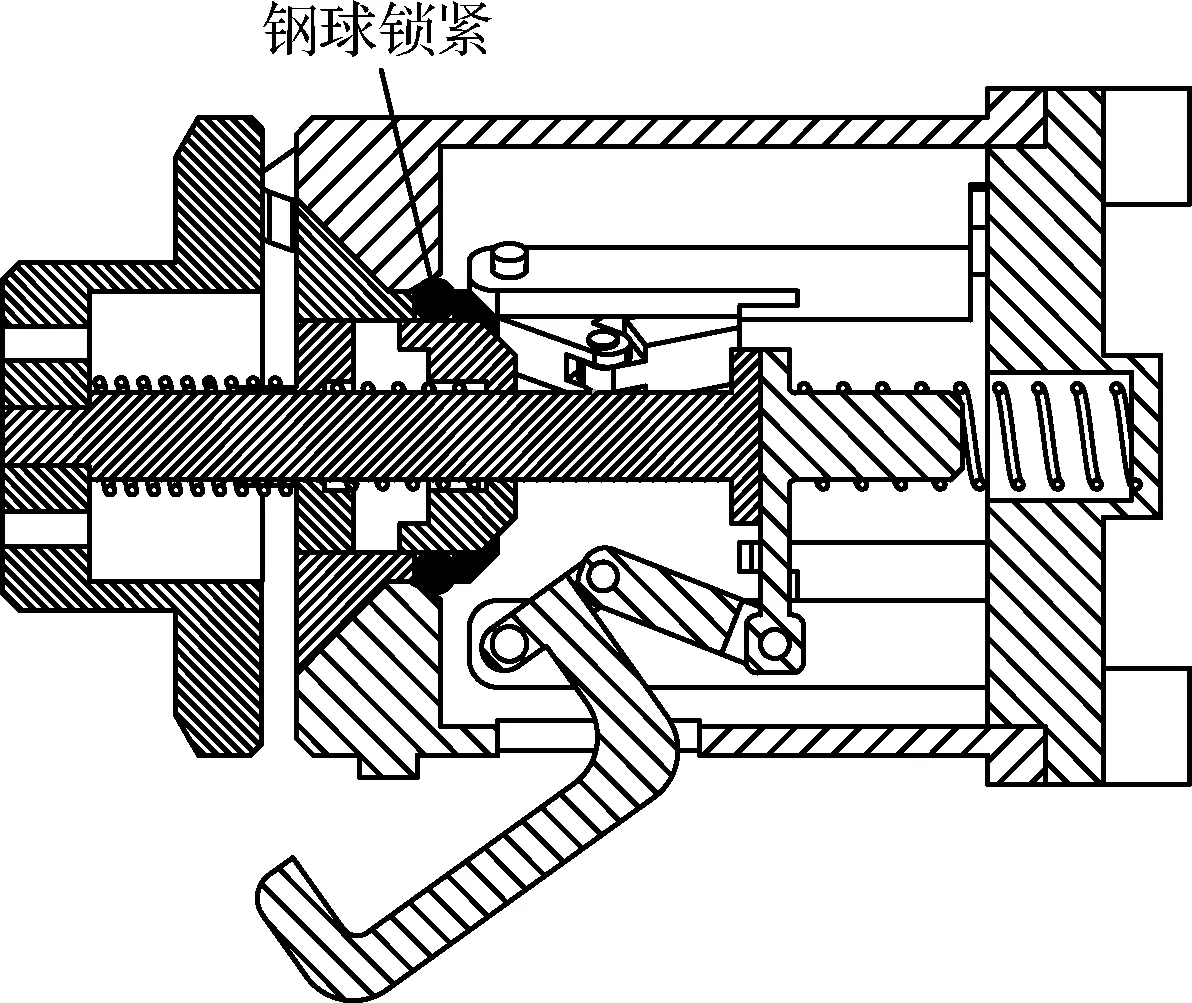
图8 钢球锁紧Fig.8 Ball lock

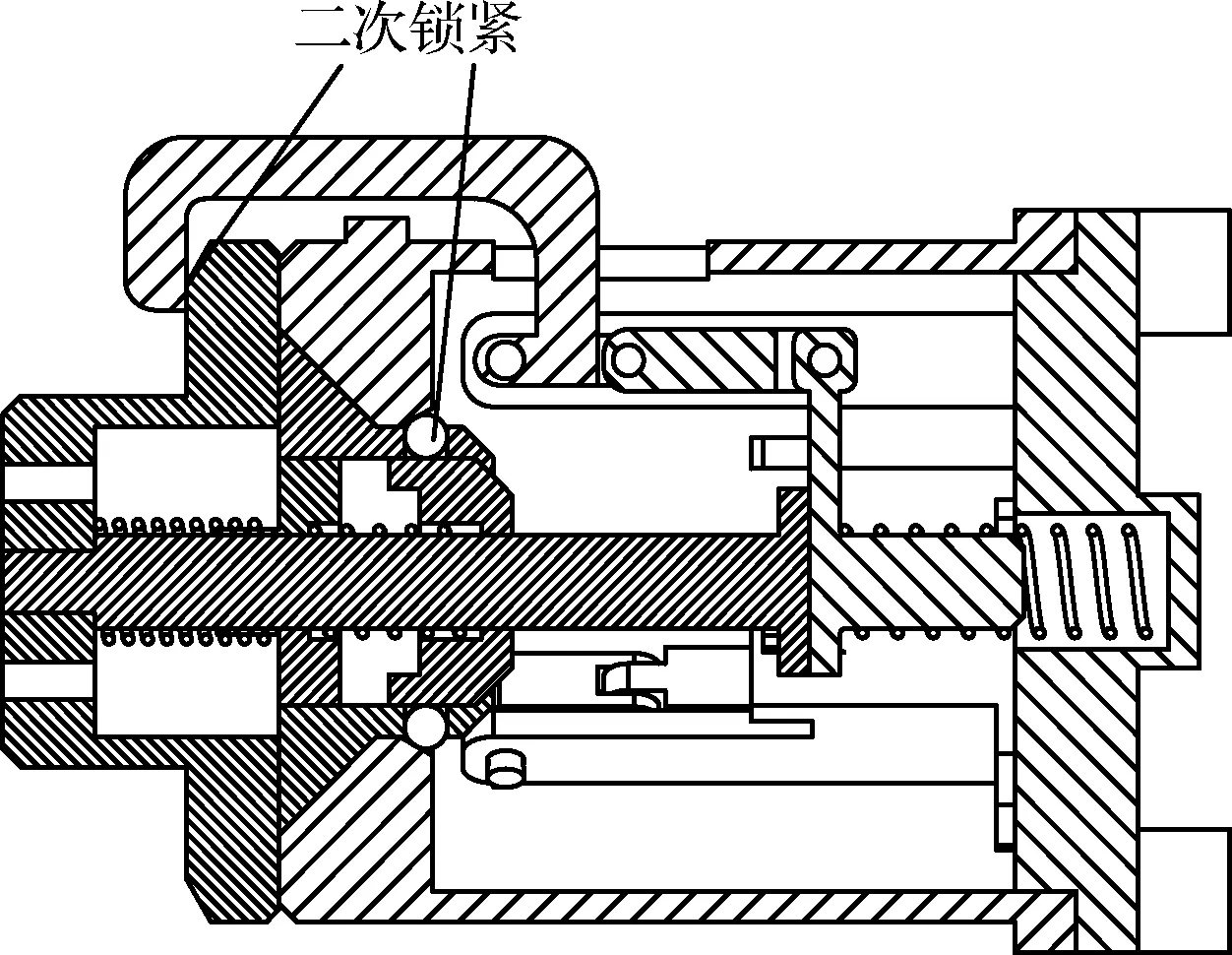
图9 锁紧爪锁紧Fig.9 Lock claw lock

如图9所示，第四阶段，推杆继续运动，导向件受到推杆的力作用,驱动曲柄滑块机构运动，当锁紧盖运动到上箱体顶部时，锁紧爪对其进行二次锁定。

2 容差性能分析

2.1 接口运动学分析

图10为组装单元对接接口的布置情况以及距离关系。可以看出，组装接口上下对称，在分析容差条件时通过分析任意一组对接接口便可表示出所有对接接口的情况。其中，D1为对接模块与对接平面中心坐标沿Z轴方向的距离，D2为上箱体顶部与底部之间的距离，D3为导向头前端中心与锁紧盖末端坐标间的距离，D4为对接模块与对接平面中心坐标沿Y轴方向的距离，D5为两组装单元中心位姿无任何偏差，开始时组装单元之间的距离。

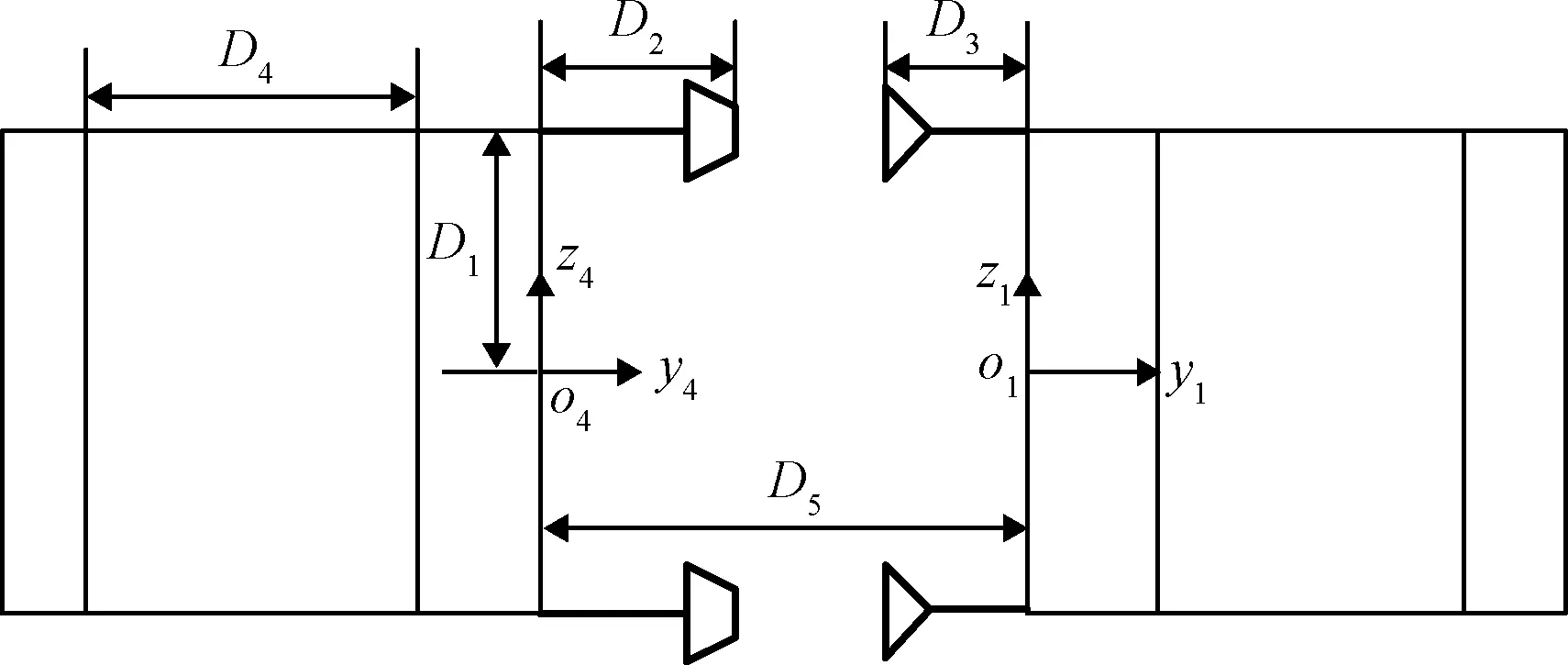
图10 组装单元尺寸Fig.10 Dimensions of assembly unit

如图11所示，在卫星载体中心建立统一参考坐标系∑O-xyz。

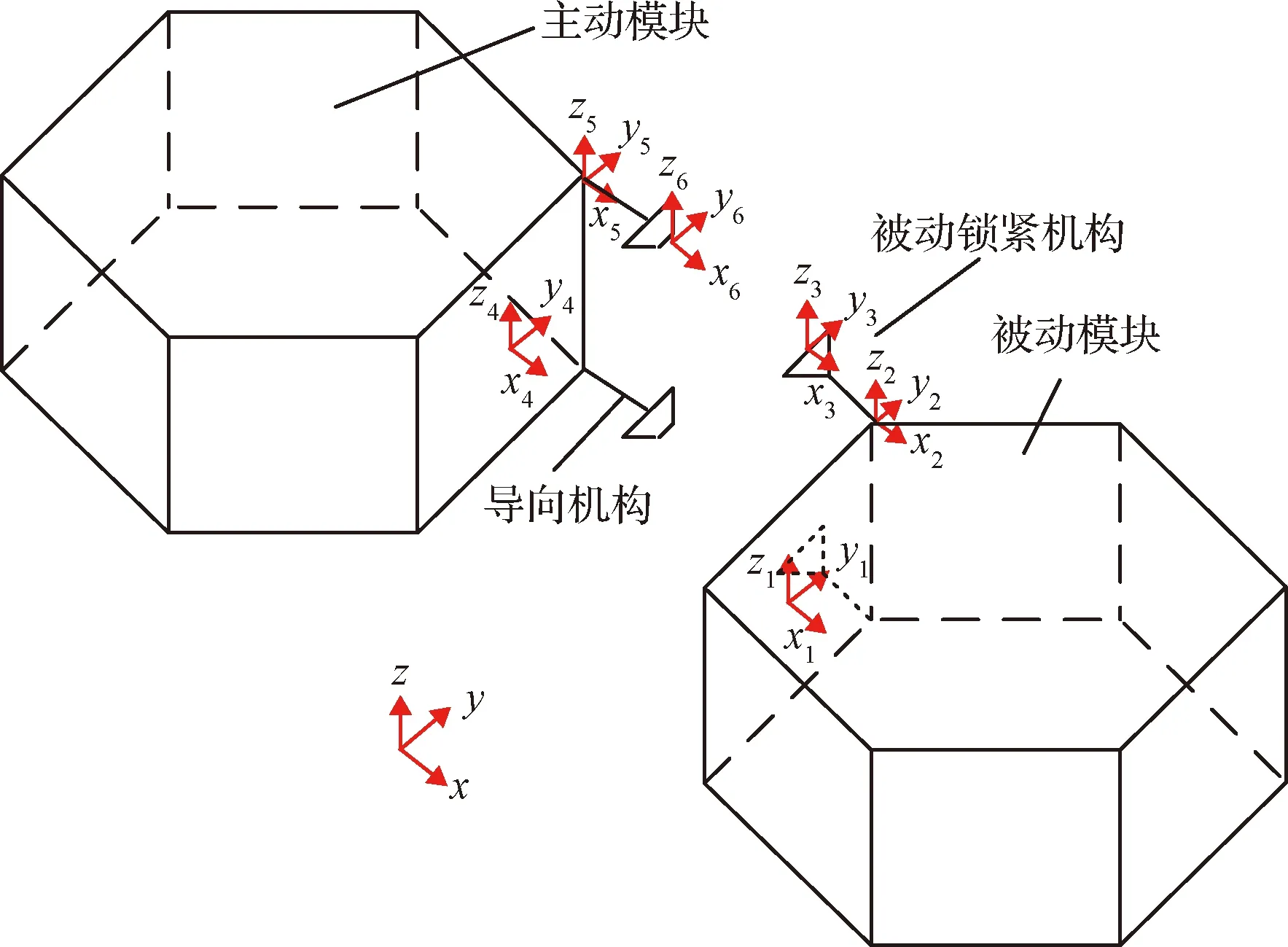
图11 两对接单元之间的坐标系Fig.11 The coordinate system between two docking units

在被动、主动单元的对接面中心分别建立∑O1-x1y1z1和∑O4-x4y4z4坐标系，在被动锁紧机构的底座末端建立∑O2-x2y2z2坐标系。在上箱体的锥型结构顶部中心和前端中心分别建立∑O3-x3y3z3和∑O6-x6y6z6坐标系，在导向机构锁紧盖中心建立∑O5-x5y5z5坐标系。

导向头前端中心与锁紧盖末端坐标系间的变换矩阵为：

(1)

上箱体顶部与底部之间的变换矩阵为：

(2)

对接模块与对接平面中心坐标系间的变换矩阵为：

(3)

(4)

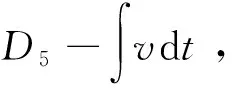
(5)

式中:d为主动对接模块中心到被动对接模块中心的距离。

综合考虑组装单元加工精度和机械臂控制精度带来的位姿偏差，推导得到机构的总位姿：

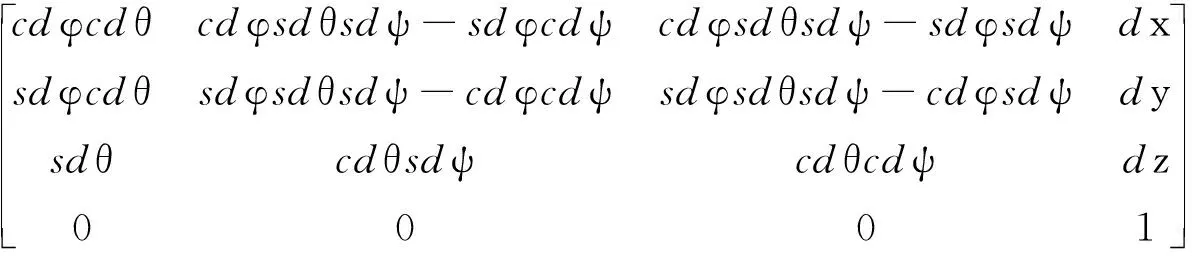
(6)

式中: cdφ=cosdφ,sdφ=sindφ，cdθ=cosdθ,sdθ=sindθ，cdψ=cosdψ,sdψ=sindψ，φ为绕z轴的角度偏差，θ为绕x轴的角度偏差，ψ为绕y轴的角度偏差,T为整个对接机构的平移变换矩阵,R为整个对接机构的旋转变换矩阵。

则真实工作环境下∑O1-x1y1z1到∑O4-x4y4z4的齐次变换矩阵为：

(7)

若∑O6-x6y6z6上有一点坐标为(x0,y0,z0)，则(x0,y0,z0)在∑O3-x3y3z3的坐标为：

(8)

2.2 容差性能理论计算

根据图12所示，在仅有一个自由度上的容差时，整个对接机构的极限位置偏差为：

Δrmax=R-r

(9)

其中,r为导向头在上箱体顶部方向上的投影半径,Δr为对接机构的位置偏差。

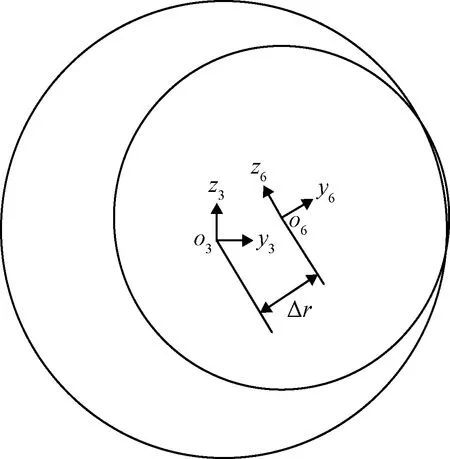
图12 对接机构最大极限偏差Fig.12 Maximum limit deviation of docking mechanism

机械臂抓取组装单元由一个向另外一个运动过程中，导向头必须在上箱体的包络范围内运动，这样才能有效的保证对接机构能够顺利的进行对接，如图13所示。

为了满足位移条件， Q点的位姿不可以超出上箱体的圆锥包络。为了满足角度条件，上箱体和导向头二者的中心距离在上箱体顶部方向上的投影距离不能大于二者的半径之差。需满足如下所示的关系约束：

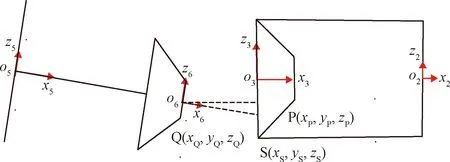
图13 导向头位姿偏差Fig.13 Steering head pose deviation

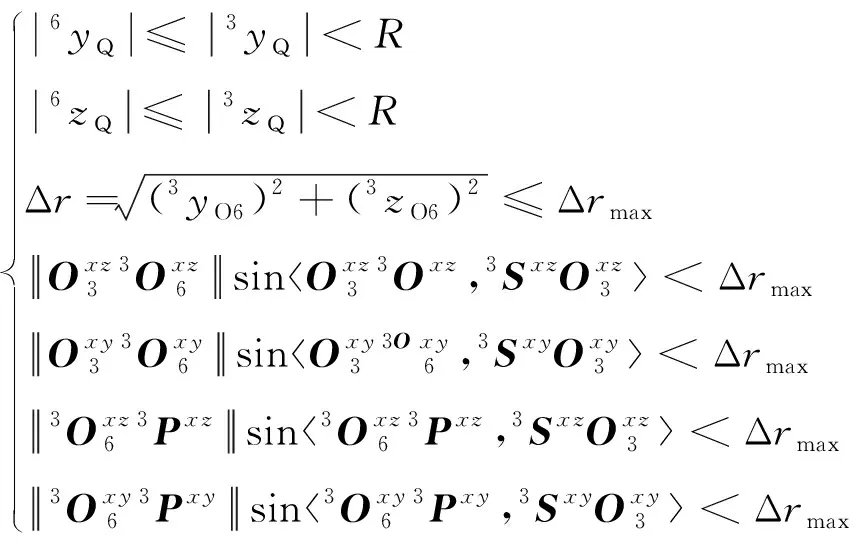
(10)

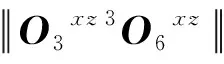
根据本文设计实物的具体尺寸，结合式(1)-式(10)，可以确定对接机构容差的可行域为：

(11)

结合上述式子能够推出各位移、角度的偏差范围，容差可行域如图14所示。

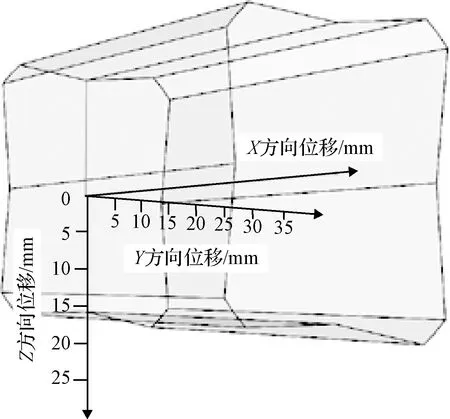
图14 容差可行域Fig.14 Tolerance feasible region

2.3 容差性能仿真分析

以各个方向的位姿为自变量，通过改变自变量来确认当各个容差作用于对接接口时，是否能够顺利的完成对接，进而证明其容差性能。取2.2节中分析得出的最大偏差量进行ADAMS仿真分析，得到5种状态下导向头与上箱体接触时力的大小以及二者的中心距离,见表1。

表1 容差仿真条件Table 1 Tolerance simulation parameter table

从图15可以看出，在各最大偏差下，对接机构均完成了对接。

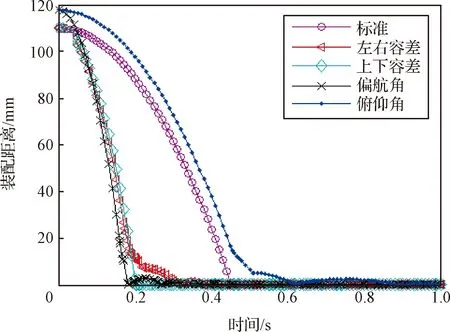
图15 对接机构装配距离变化关系Fig.15 Relationship between assembly distance of docking mechanism

3 单模块装配影响因素分析

在单元对接过程中会产生冲击，为评估冲击的大小，引入接触力。如图16所示，在ADAMS中建立对接机构仿真模型，推力设置为10 N，方向指向锁紧机构。

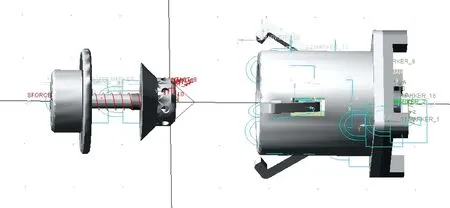
图16 仿真模型Fig.16 Simulation model

3.1 摩擦系数的影响分析

首先分析对接过程产生的冲击与静摩擦系数的关系，在仿真分析时，设置对接机构为零偏差，设置上箱体与导向头的接触刚度为100000 N/mm(参照文献[22]中钢与钢之间干摩擦状态下的接触刚度进行取值)、推力为10 N、动摩擦系数为0.1，上箱体锥角为45°，如图17所示,为接触力峰值曲线图。

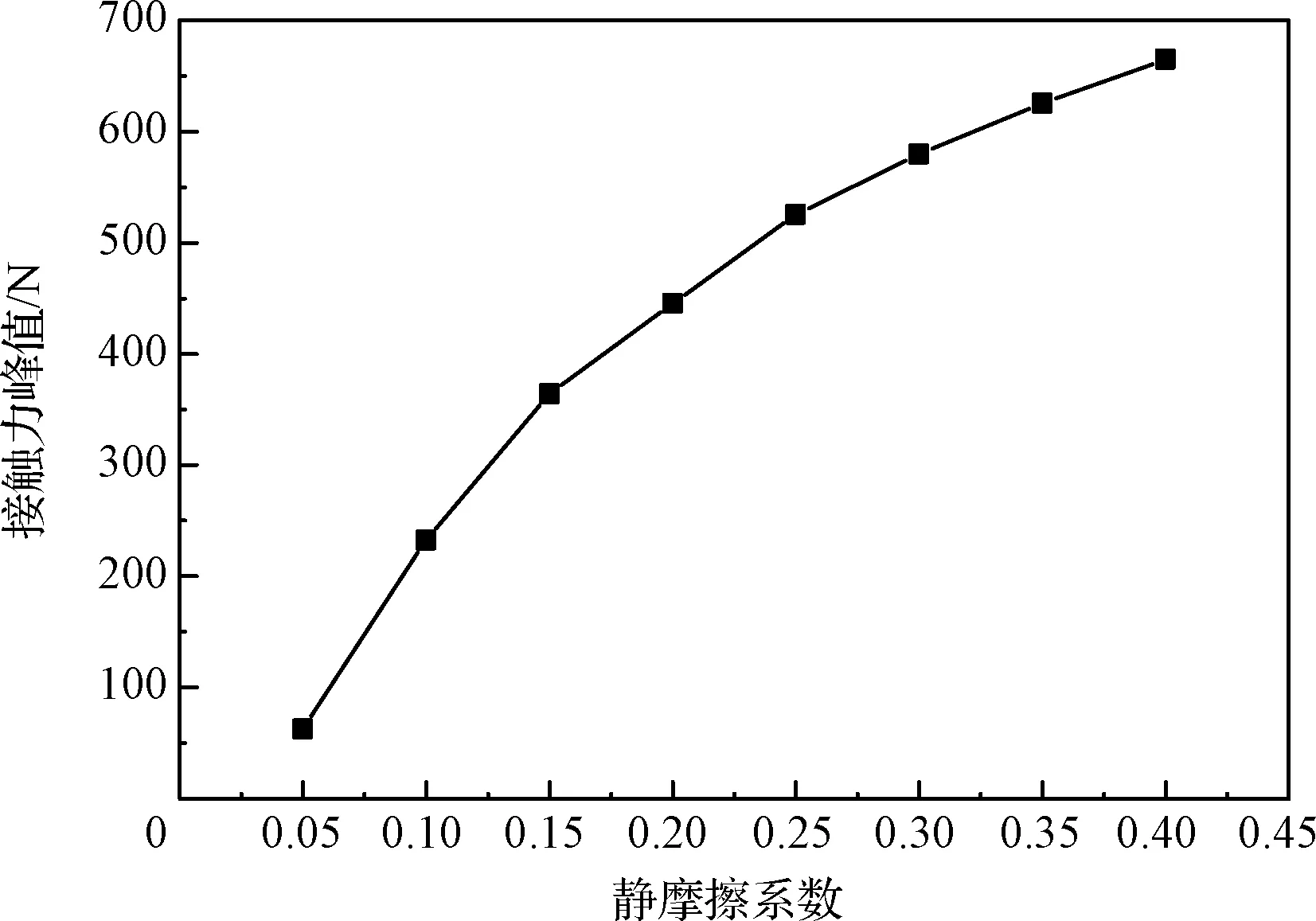
图17 静摩擦系数影响曲线Fig.17 Influence curve of static friction coefficient

ADAMS中动静摩擦系数随着相对滑移速度自动切换，呈非线性变化规律[22]。从图17中可以看出，由于本文静摩擦系数不同，系统在相同的推力作用下，其相对滑移速度不同，计算得出的碰撞接触力增长规律呈逐渐减慢的非线性。

以动摩擦系数为自变量，设置静摩擦系数为0.3，其余参数不变进行仿真分析。

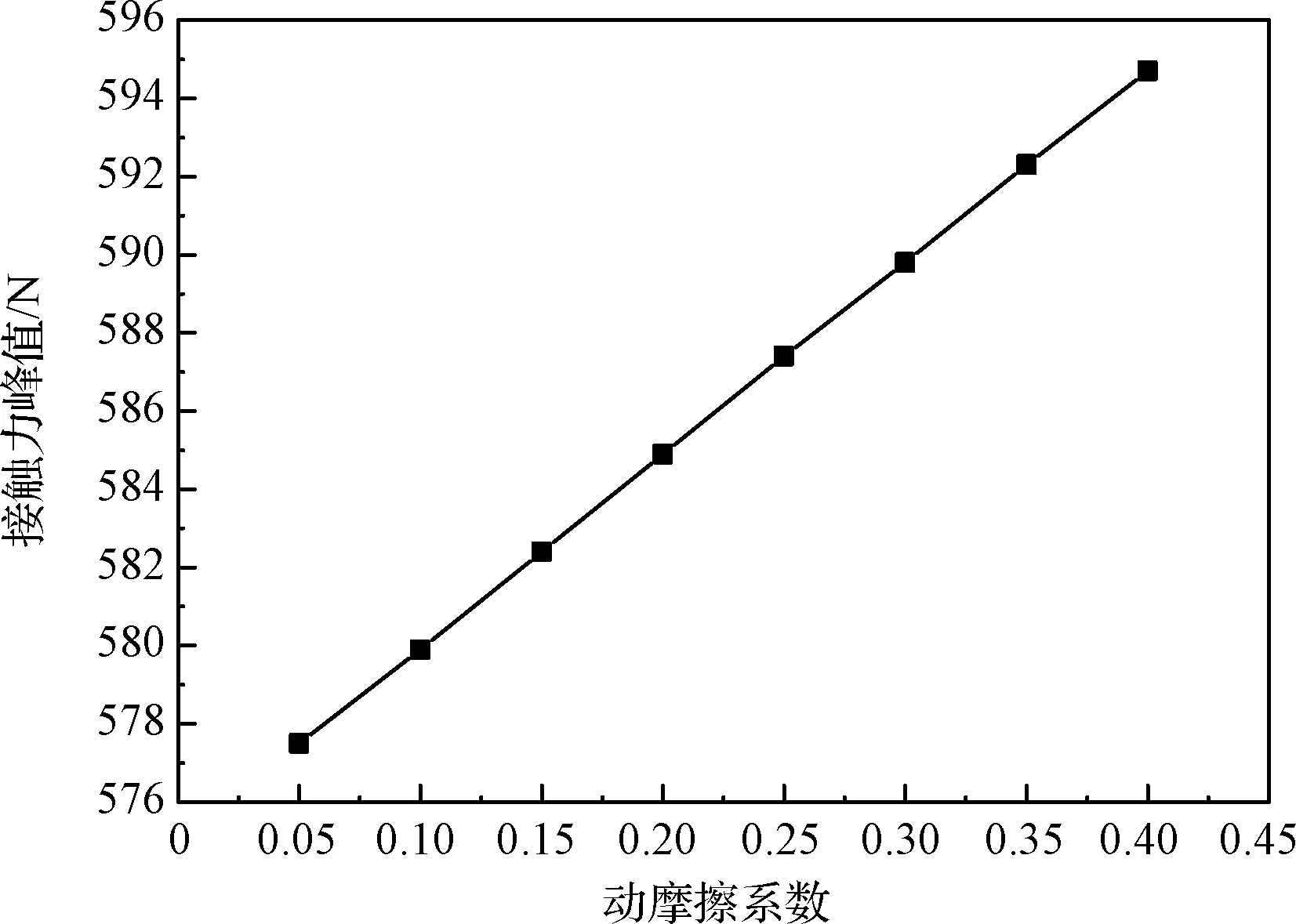
图18 动摩擦系数影响曲线Fig.18 Influence curve of dynamic friction coefficient

从图18中可以看出，物体在相同推力和静摩擦系数下，在克服静摩擦力开始运动后,初始的相对滑移速度相等，动摩擦系数影响规律呈线性关系。

动摩擦系数变化所引起的接触力变化没有静摩擦系数大，在设计时应尽量减少静摩擦系数。

3.2 推力的影响分析

以机械臂推力为自变量，静摩擦系数0.3、动摩擦系数0.1，其余参数不变进行仿真分析。

图19 推力影响曲线Fig.19 Thrust influence curve

导向头与上箱体之间的主要接触方式为冲击式接触，由于推力的增加导致对接时速度的增加，通过文献[22]可知，在ADAMS软件中接触采用线性等效弹簧阻尼模型计算，具有强烈的非线性、非保守特性。从图19中可以得出，接触力随推力增大而增大，在推力增大到6 N之后，接触力迅速增大，到8 N之后接触力增加、速度降低，整体规律呈非线性。所以，既要将推力降到最低又要满足对接所需的最小值，最终实现冲击的降低，提高对接平稳性。

3.3 锥角影响分析

以碰撞锥角为自变量，其余参数不变进行仿真分析。

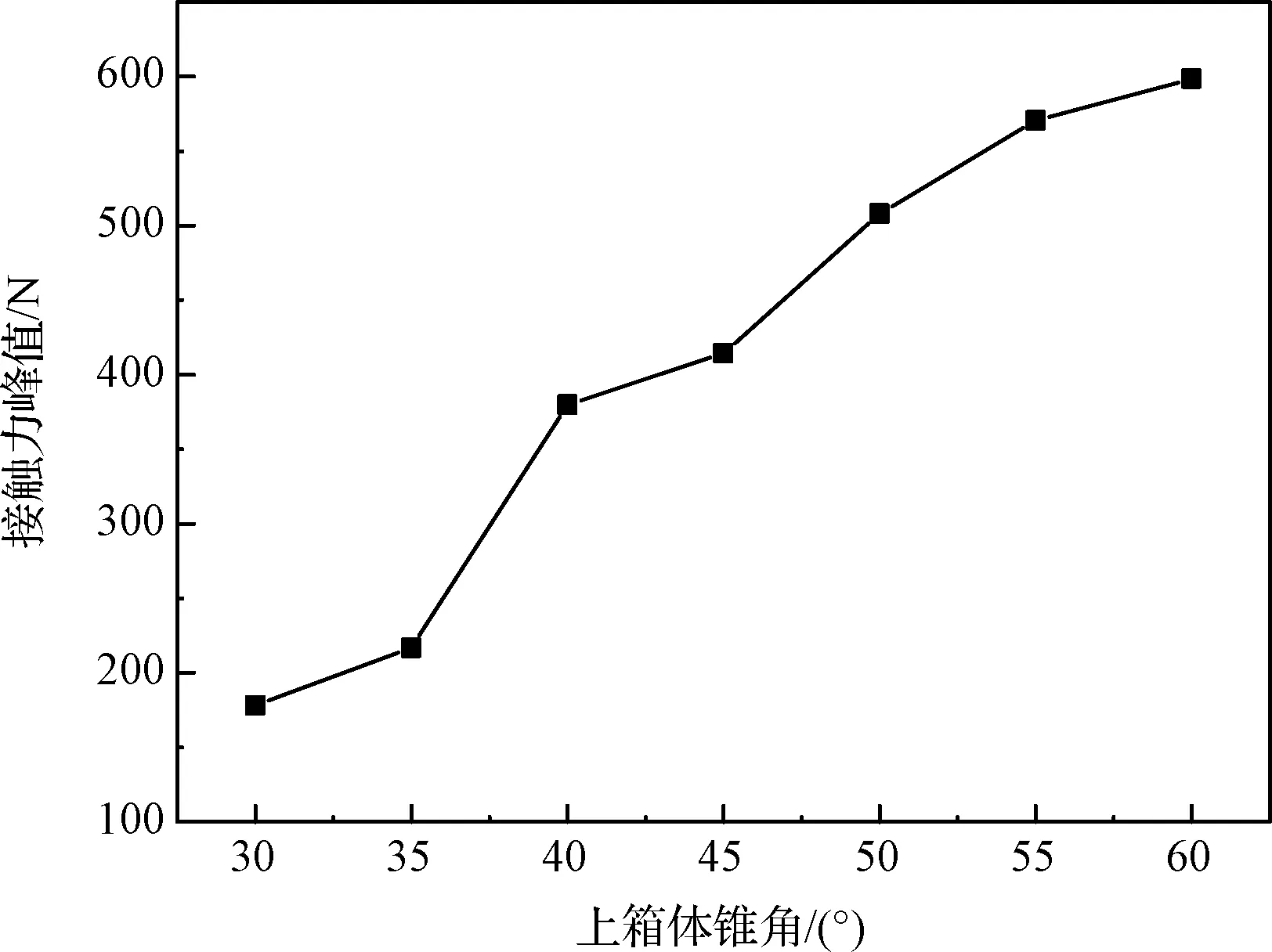
图20 锥角影响曲线Fig.20 Cone angle influence curve

锥角的增大导致接触时的对接速度方向发生变化，接触力与锥角成正相关的关系。在ADAMS软件中接触具有强烈的非线性、非保守特性。从图20中可以得出接触力随着锥角的增大而增大，增长的趋势呈先陡后缓的状态。因此，在设计锥角时，应采用小锥角，同时为了对接的准确性，还要满足位姿容差。

4 结 论

本文首先提出了一种新型的适用于在轨组装的三爪式对接接口方案并完成了相关的设计。其次，建立了对接结构位移和角度容差的理论模型，得出X方向容差为14.25 mm，Z方向容差为15.84 mm，绕X轴角度容差为5.65°，绕Y轴角度容差为5.51°，绕Z轴角度容差为5.34°，利用ADAMS软件仿真验证了理论模型的正确性。最后，通过改变动、静摩擦系数、机械臂推力及碰撞锥角，对接口对接情况进行了仿真分析，得出了对接机构接触力大小与静摩擦系数、机械臂推力与碰撞锥角之间的非线性影响关系，提出了可以减小碰撞冲击、使对接更加稳定可靠的设计建议，为实际工程设计提供了参考。