地月Halo与DRO支持的往返月球任务轨道

曾 豪，李朝玉,徐 瑞，郝 平，彭 坤

(1.北京空间飞行器总体设计部，北京 100094；2.北京理工大学，北京 100081)

0 引 言

独特的空间环境观测位置与行星际探测的低耗能中转站使得三体系统平动点在空间任务中的应用价值逐步凸显[1-3]。地月系统平动点轨道能够为月球探测中继星的部署提供落脚点，支持着陆器与巡视器的月球背面导航任务[4-5]。借助地月空间拟周期轨道分析月球磁性层与空间环境[6]。其次，地月L1点与L2点计划用于未来载人空间任务，将空间站部署于月球附近三体平动点轨道，能够完成空间物资运输与燃料补加[7-8]、载人火星[9]与小行星探测任务[10]。同时，通过月球引力辅助与不变流形理论能够实现飞行器由地球停泊轨道与平动点轨道之间的低能量转移，从而有效地提高飞行器携带有效载荷的能力，将飞行器的月球探测任务作用最大化。

针对三体轨道支持的登月往返任务研究，彭坤等[11]分析了空间站部署地月平动点Halo的载人月球探测飞行模式，从燃耗需求、登月窗口和可靠性等多方面进行优劣分析与定量评价，分析表明基于L2点Halo的空间站登月模式可以为载人深空探测任务提供支持。Whitley等[8]针对月球附近的近直线Halo轨道与环月轨道(LLO)间往返时间与速度增量等参数变化特性及全月面可达域进行研究。同样地，曹鹏飞等提出了一种设计变量解析初值搜索策略，结合不变流形与局部梯度优化对探测器由Halo轨道飞抵LLO的两脉冲转移特性与奔月轨道月面可达范围进行分析[12]。Gao等针对嫦娥2号探测器环绕地月平动点轨道的潜在拓展性试验进行分析，借助稳定流形分别设计了环月轨道飞抵地月L1点与L2点Halo轨道的三脉冲轨迹[13]。Mingotti等[14]结合小推力技术与不变流形理论，采用离散配点法实现了不稳定流形与环月轨道的最优小推力拼接，但存在任务飞行时间长等问题。

地月系统三体轨道与环月轨道之间构造最优转移轨迹需要综合分析多天体引力相互影响下的复杂动力学特性。同时，三体轨道与环月轨道离轨点、捕获点位置的确定，将对轨道转移燃耗、时间等性能指标产生影响。因此，如何考虑约束模型，如何借助空间流形快速构造初始转移轨迹，如何调整离轨点与捕获点确定燃料最优轨迹的同时有效地缩短飞行时间，均是飞行器往返三体轨道与月球轨道设计时亟需重点考虑和解决的问题。

结合以上问题，同时考虑到Lambert理论求解两点边值问题时[15]，二体模型与三体模型差异导致的部分工况轨道设计初值收敛性较差的问题。本文直接以三体模型下平动点轨道与不变流形构型为基础，通过微分修正迭代求解初始转移轨迹，确定设计变量初值。然后采用配点法与局部优化算法(SQP)，构造出满足近月点约束的环月轨道与平动点轨道之间燃料最优往返转移。设计过程中采用时间变量表征三体轨道上状态量，迭代优化求解确定转移轨道最佳的离轨点与捕获点。本文以月球附近Halo与DRO为研究对象，对不同幅值三体轨道、环月轨道倾角及任务飞行时间对变轨机动增量的影响重点分析，验证所提设计方法的有效性与通用性，为未来登月任务规划提供理论支持与数据借鉴。

1 轨道设计模型与研究目标

1.1 圆型限制性三体模型

针对飞行器往返环月轨道与三体轨道的空间状态变化特性分析，本文以地球、月球及飞行器组成的圆型限制性三体模型(CR3BP)进行研究，如图1所示。

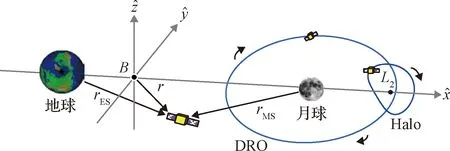
图1 会合坐标系与三体轨道Fig.1 Rotating reference frame and three-body orbits

根据能量法并对时间、质量、长度等参数无量纲化处理，飞行器在质心会合坐标系下的动力学模型为：

(1)

式中:

(2)

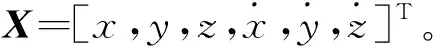
1.2 三体轨道与状态转移矩阵

在地月三体空间中，月球附近包含着构型各异的周期轨道，本文基于大幅值逆行轨道(Distant retrogr-ade orbit,DRO)与晕轨道(Halo orbit,Halo)两种类型的往返轨迹进行设计与特性分析，如图2所示。

Halo轨道为平动点附近的晕轨道，通过L2点Halo轨道能够实现对月球背面可见(嫦娥四号中继星任务轨道)。同时，由图2(a)与(b)可知，Halo轨道附近稳定流形与不稳定流形，能够为往返轨道设计提供帮助。

DRO轨道为围绕月球的逆向运行共振轨道。研究可知，DRO具有Lyapunov稳定性，虽然空间天体引力会破坏DRO的稳定性，但此轨道仍适合于长时间的天体绕飞任务与日地观测任务[16]。

在CR3BP模型中设计转移轨道与不变流形时，可采用状态转移矩阵描述下一时刻对当前时刻状态量的敏感性，提高轨道计算效率与降低设计难度，满足：

(3)

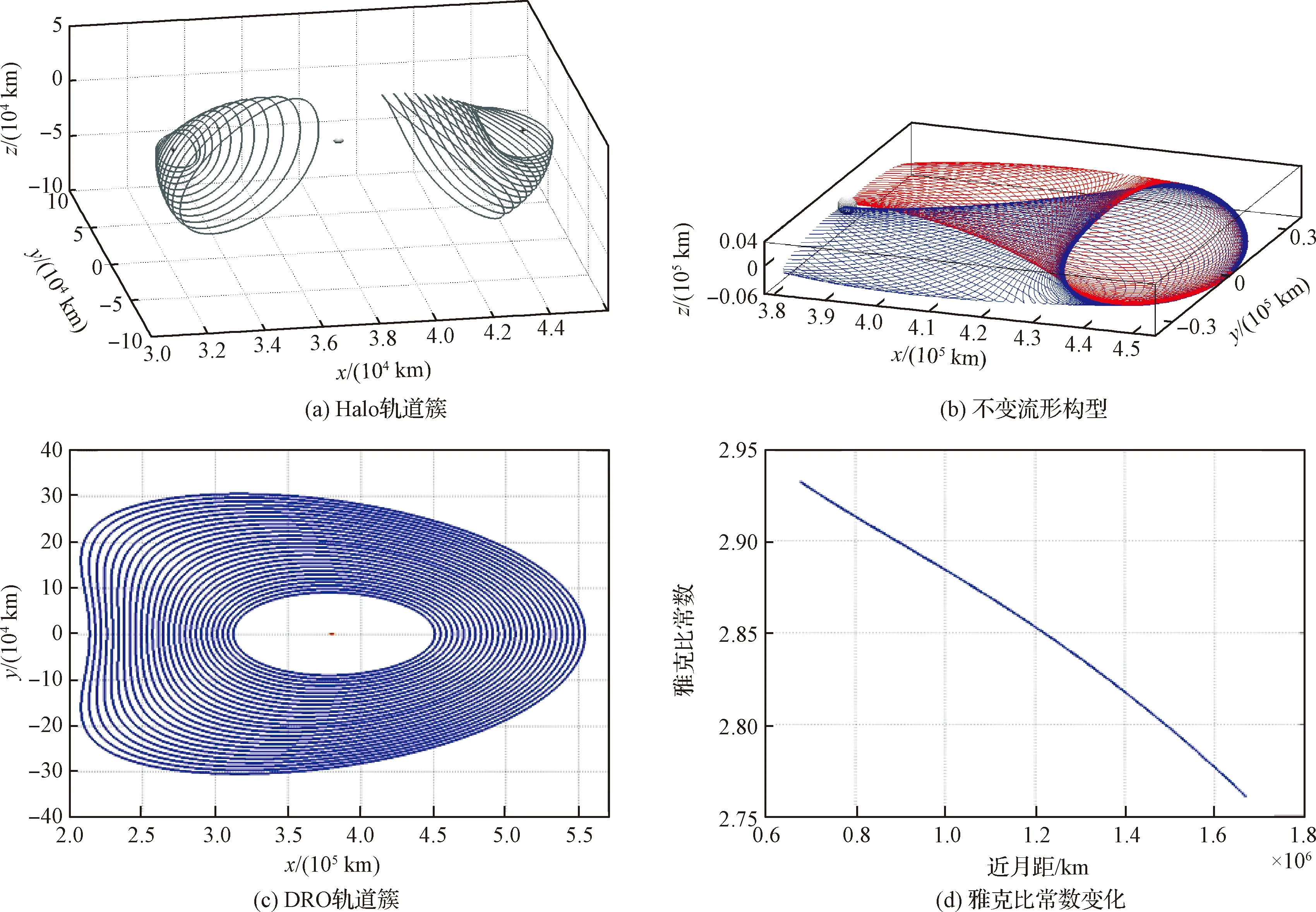
图2 地月空间Halo与DRO分布特性Fig.2 Characteristic of Halo and DRO in cislunar space

2 约束模型与设计方案分析

2.1 往返轨迹约束建模

针对环月轨道与三体轨道之间往返特性分析，为降低轨道设计难度，本文直接以三体轨道与不变流形为基础，构造燃料最优飞行轨迹，如图3(a)所示。

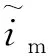
为了更好利用三体平动点轨道特性降低设计难度，基于逆向积分策略进行往返轨迹求解。通过时间变量τ表征三体轨道对应时刻的状态量，优化搜索τ可快速地确定去程离轨点与回程捕获点最佳位置。同时，为了设计出满足给定约束的最优转移轨迹，结合多重打靶法与序列二次规划算法对初始参考轨道进行分段处理，能够有效降低设计参数的敏感性。

具体地，最优轨迹求解时设计变量C包含去程三体轨道离轨点或者回程捕获点时间变量τ与三轴速度增量ΔVOI、拼接点之间飞行时间Ti及状态量Xi。设计变量与约束方程满足：

(4)

C1=[ΔVOI,Tf]T

(5)

若限制转移时间固定，则在式(4)中考虑时间约束，即T1+T2+…+Tn-1=T*。

图3 月球往返转移与多重配点策略示意图Fig.3 Diagram of round-trip transfers and multiple collocation strategy

2.2 设计初值猜想策略

针对设计变量初值搜索问题，Halo轨道附近存在着不稳定流形与稳定流形，可以通过施加脉冲对不变流形结构进行调整，使得转移轨道终端满足约束方程中部分条件。而DRO轨道较为稳定，无法基于空间流形确定轨道初值，但DRO为平面周期轨道，关于y轴近似对称，同样能够通过调整速度增量确定合适的初始转移轨道，如图4所示。

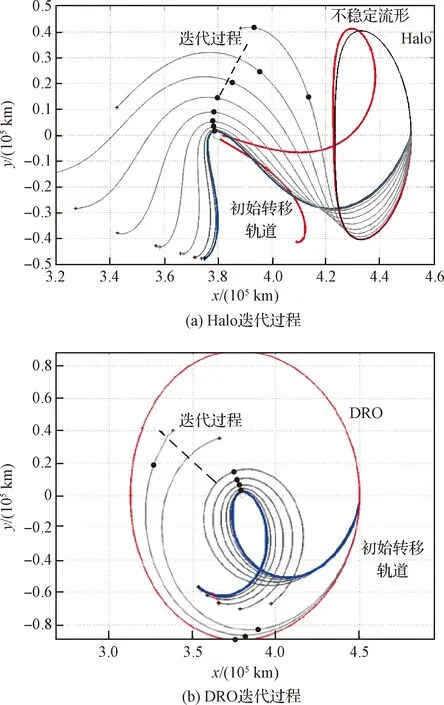
图4 初始参考轨迹迭代过程Fig.4 Iteration process of designing initial reference path

具体设计步骤可描述为(以去程轨迹为例)：

1)构造目标三体Halo轨道与DRO轨道，初步选取离轨点，合适的位置位于xy平面内x轴向距离月球最远端附近。

2)确定Halo轨道不稳定流形与DRO轨道上航迹角为零的位置，如图4中圆点所示，进而确定转移时间Tf。

3)结合微分修正算法，考虑转移终端环月轨道高度hm与航迹角γm约束，迭代修正设计变量C1，能够快速设计出满足约束的转移轨迹，如图4所示。

微分修正算法中需要结合状态转移矩阵和轨道末端点状态量，确定约束变量关于自由变量的微分关系式，即:

(6)

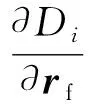
针对环月轨道高度约束，满足:

(7)

其中:rm=rf-[1-μ,0,0]T。

飞行航迹角关于状态量的偏导数为:

(8)

2.3 局部优化约束方程梯度信息

上述轨道初值求解策略仅满足环月轨道高度与航迹角约束，且三体轨道离轨点(或捕获点)相对固定，无法保证转移方案的最优性。应通过局部优化SQP算法对设计变量进一步迭代求解，确定最优轨迹的设计变量参数值。同时，结合多重打靶法对初始参考轨道分段处理降低轨道设计难度。目标函数满足:

(9)

推导目标函数、约束方程的梯度关系。其中，目标函数仅包含为ΔVOI与ΔVLMO，即:

(10)

近月点轨道高度与相对月球航迹角的偏导数如式(7)与式(8)所示。类倾角及其关于末端点状态量的微分关系满足:

(11)

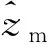
根据链式法则与矢量运算法则:

(12)

其次，拼接点位置与速度矢量约束关于设计变量的梯度满足:

(13)

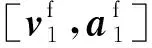
(14)

若考虑转移时间约束，则拼接点时间偏导数∂Ti/∂Ti=1。约束方程的梯度矩阵阶数为(6n-2)×(7n+1)，部分项由式(7)～(14)构成，其他项均为零。

3 月球往返轨道方案分析

本文基于地月空间限制性三体系统及月球往返轨道设计方法，分析不同构型Halo与DRO转移轨道特性，重点讨论环月轨道倾角与三体轨道幅值变化对任务燃耗与飞行时间的影响。在任务规划时，设定环月轨道高度300 km，相对月球的飞行航迹角为0°。

3.1 基于Halo轨道的月球往返轨道设计

3.1.1往返转移轨道特性分析

图5描述了考虑环月轨道类倾角90°，目标Halo轨道法向幅值8000 km，飞行时间分别为2天与3.5天往返转移轨迹。由图可知，不同工况下Halo轨道上合适的离轨点与捕获点位于远离月球一端的弧段，环月轨道机动点分布于xy平面附近。针对2天往返转移轨道，飞行器施加292.863 m/s速度增量从Halo轨道上离轨，飞行2天后在近月点沿速度方向机动614.713 m/s完成环月轨道捕获，回程轨迹中环月轨道与Halo轨道机动速度增量分别为617.469 m/s与262.084 m/s。

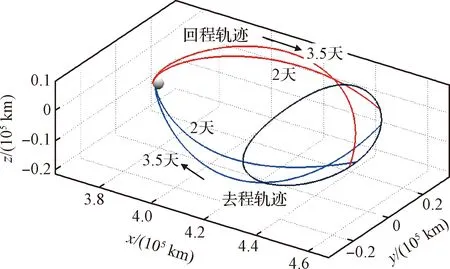
图5 Halo轨道往返最优Fig.5 The round-trip optimal transfers of Halo scenario

针对3.5天往返转移任务，去程与回程轨迹在Halo轨道上变轨机动分别为161.354 m/s与144.963 m/s，环月轨道上特征点变轨速度增量分别为600.337 m/s与603.351 m/s。比较两种工况可知，增加转移时间，能够一定程度上降低燃料消耗，即去程降低145.885 m/s与回程减少131.239 m/s。若为载人登月任务轨道，时间增加1.5天后需要考虑热控、食品消耗等因素的影响。因此，需要根据任务指标综合考虑燃耗与其他消耗选取飞行轨迹。

为了更好地给出环月轨道倾角与飞行时间对速度增量的影响，对固定飞行时间区间T∈(2.0, 3.5)天，环月轨道类倾角(10°，170°)(即月球低纬度至高纬度)的转移轨道特性进行分析，如图6所示。由图可知：1)针对Halo转移方案，在给定的时间范围内，随着飞行时间的增加，往返转移速度增量总体呈现下降趋势。2)固定飞行时间，随着类倾角逐步增大，相比于小倾角工况，完成大倾角转移任务所需速度增量增加。3)去程轨迹与回程轨迹速度增量范围分别介于(716.883，915.823)m/s与(702.589，938.409)m/s。

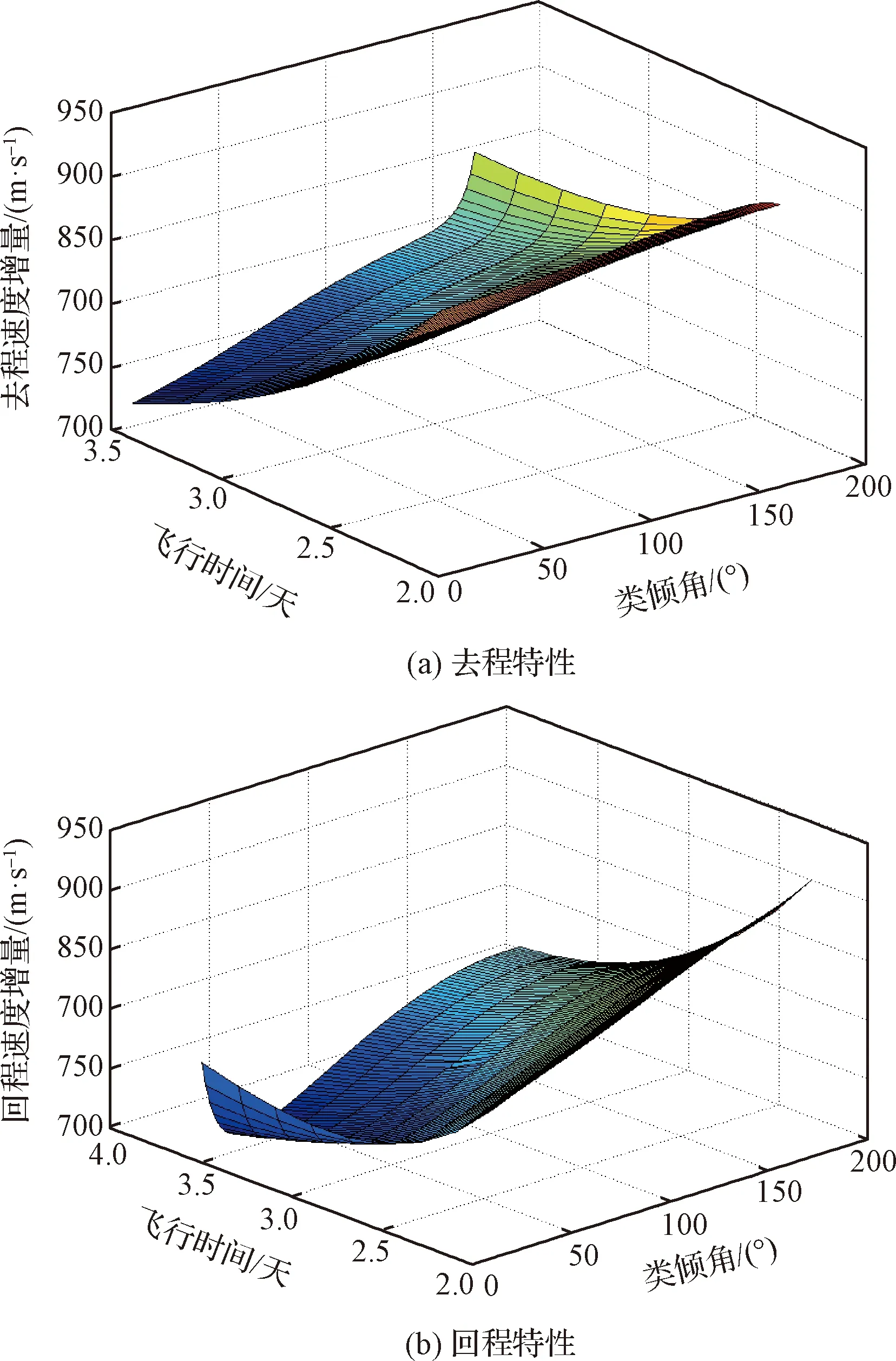
图6 飞行时间、类倾角与速度增量的变化关系Fig.6 The maps of time, velocity increment and analogy inclination

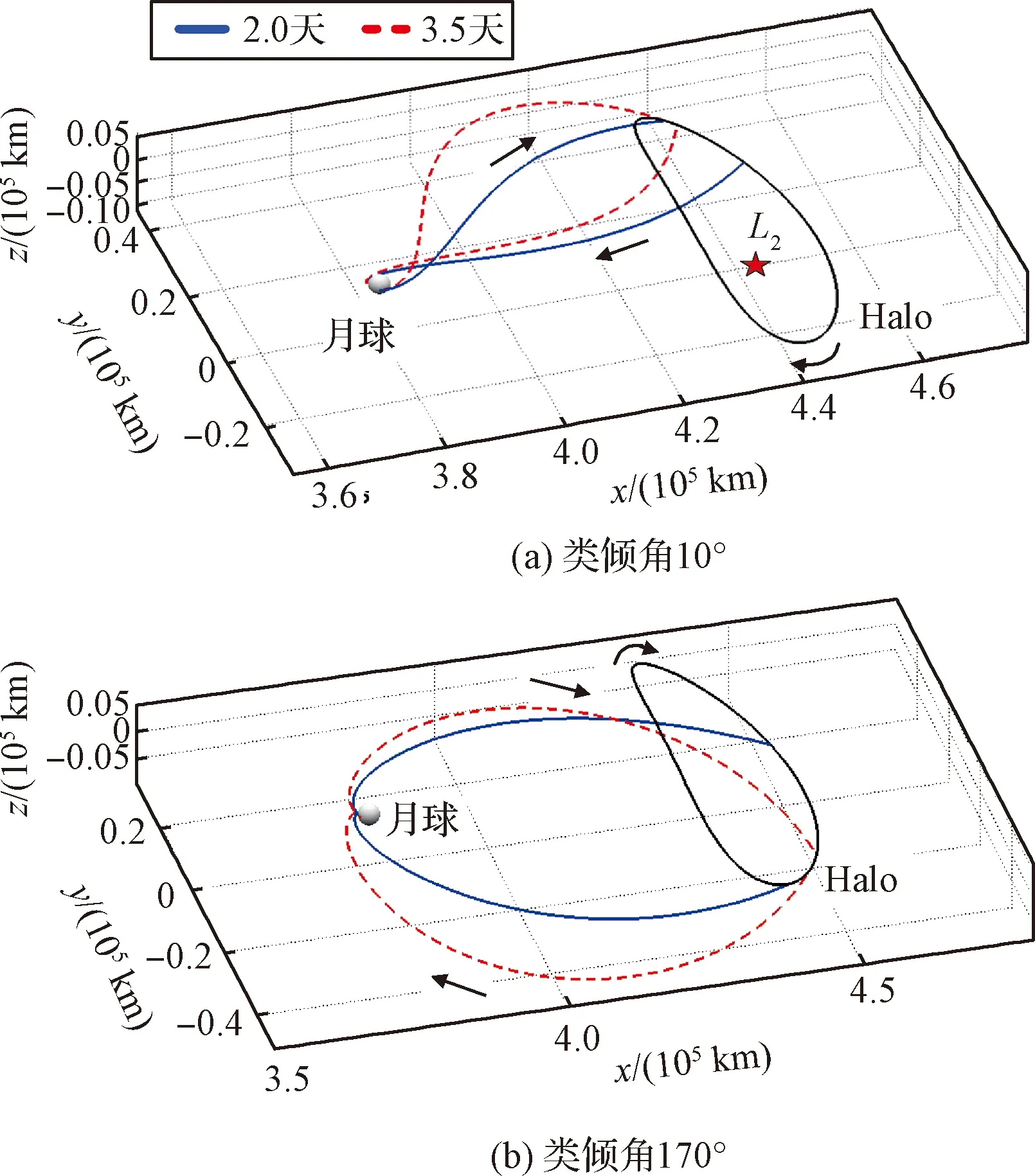
图7 类倾角10°与170°的往返转移轨迹Fig.7 Round-trip transfers of analogy inclination 10°and 170°

3.1.2Halo法向幅值对转移效果的影响

分析不同幅值Halo轨道的转移特性，能够为轨道尺寸的选取提供依据。本文针对法向幅值介于[5000, 27000]km(每隔1000 km进行取值)的去程转移轨迹，以及变轨增量、任务时间参数变化进行分析，如图8与图9所示。

对比飞行轨道及各项关键参数，不同Halo法向幅值的转移轨道离轨点分布与环月轨道捕获点位置相近。转移总速度增量随着法向幅值的增大而逐步减小，介于(647.056，808.365)m/s，其中飞行器离轨机动满足42.367 m/s与196.985 m/s范围内。飞行时间呈现增大趋势，但改变量较小，仅为5.829-5.577=0.252天。

当Halo轨道法向幅值为5000 km时，飞行器完成离轨机动后195.460 m/s，飞行5.586天后施加增量611.441 m/s完成月球捕获机动。当法向幅值为27000 km时，飞行器在Halo轨道上离轨速度增量为66.777 m/s，航行5.811天后在上施加604.364 m/s进入目标环月轨道。

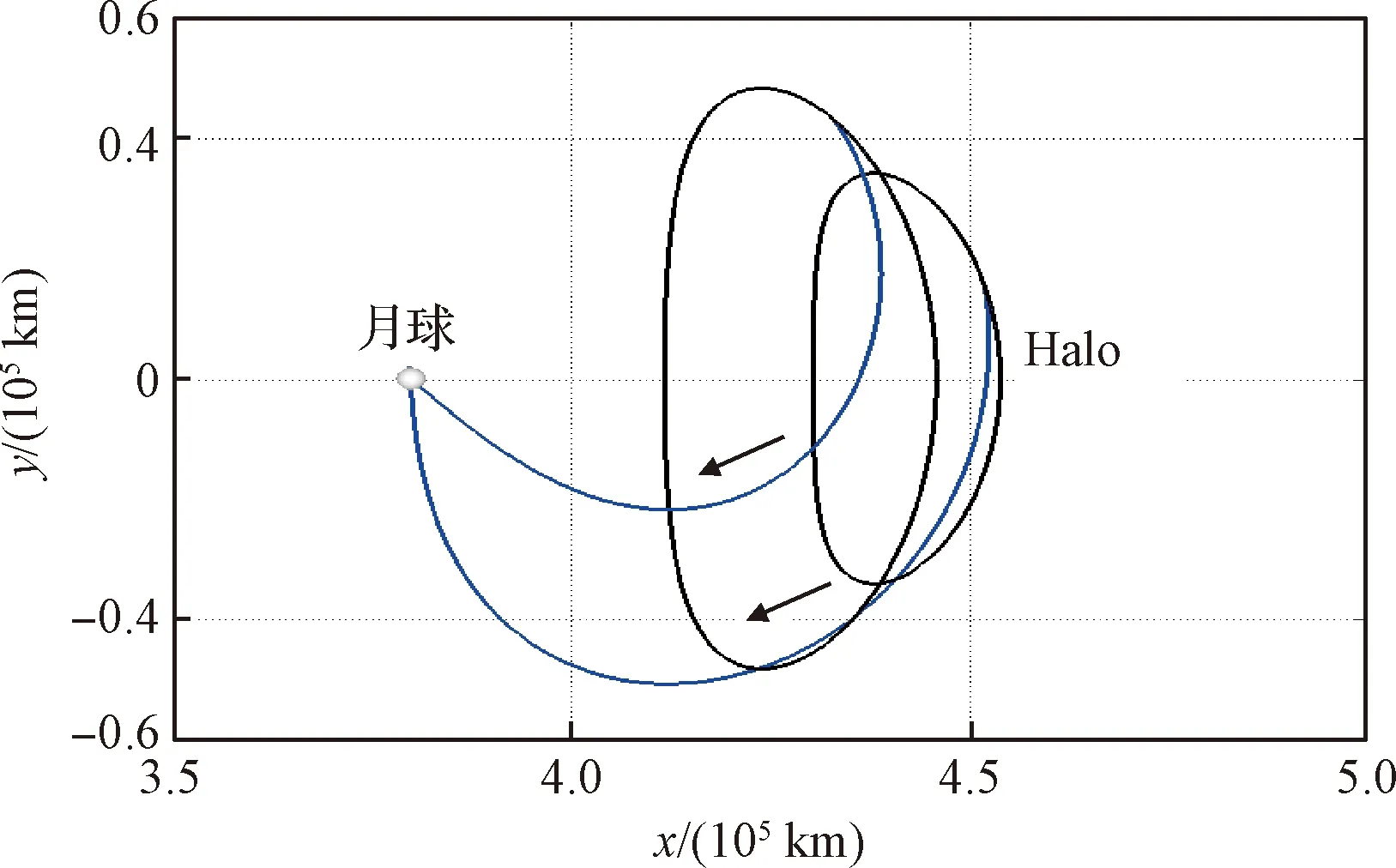
图8 Halo-月球往返转移轨迹Fig.8 Round-trip transfer orbit between Halo and the Moon

图9 不同条件的Halo转移变轨增量与时间变化Fig.9 The curves of impulse increment and transfer time of different Halo scenarios

3.2 基于DRO的月球往返转移特性分析

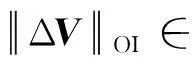
针对飞行器去程与回程速度增量与飞行时间对比分析，速度增量最小差值与最大差值分别为0.117 m/s(类倾角66°)与1.014 m/s(类倾角10°)。具体地，当环月轨道类倾角为10°时，飞行器完成月球往返转移约8.65天，近月点施加的速度增量为628.812 m/s与629.072 m/s，实现DRO离轨与捕获变轨分别为125.723 m/s与126.478 m/s。

图10 环月轨道-DRO最优转移轨迹Fig.10 The optimal round-trip transfers between the LMO and DRO

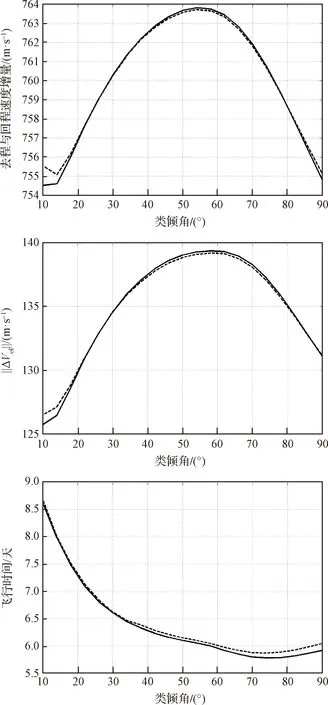
图11 不同类倾角下速度增量与转移时间变化关系Fig.11 The relationship of velocity increment and transfer time in different scenarios

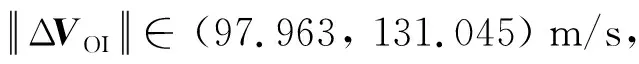
其次，针对固定时间转移任务，即5.917天，总机动增量变化曲线如图12(b)所示。随着雅克比常数逐步增加，速度增量变化满足743.176 m/s至762.974 m/s，此工况下，飞行器实现小雅克比常数DRO转移任务所需的速度增量增加。最小速度增量位于C=2.918086，完成任务总速度增量为743.176 m/s，其中离轨点速度增量113.688 m/s，月球捕获机动629.488 m/s。

图12 可变与固定时间的机动参数变化曲线Fig.12 The curve of impulse increment at a variable and fixed time

3.3 关键参数对比分析

分析地月平动点Halo与DRO轨道支持的登月模式的燃耗需求与时间需求，图6与图11燃料最优设计结果见表1。

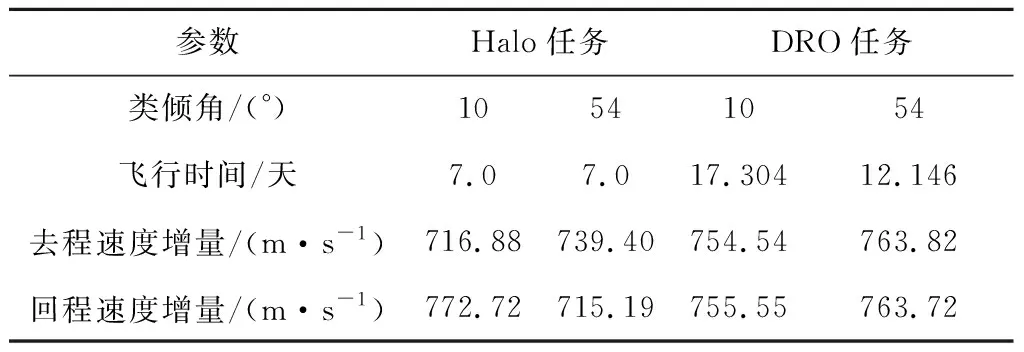
表1 不同月球往返轨道的速度增量与时间需求Table 1 Demand for velocity increment and flight time for different orbits in lunar exploration

对比Halo与DRO两种模式的往返环月轨道的转移方案，完成Halo与DRO转移任务需要的机动增量相当，但Halo转移更适合于短时间任务。DRO模式为降低任务燃耗，转移时间将会增加。应注意，三体轨道幅值(即雅克比常数)对转移任务指标存在一定的影响，需根据实际任务需求确定轨道幅值。

4 结 论

本文针对飞行器往返月球附近Halo或DRO与环月轨道设计问题，结合不变流形理论与三体轨道构型特性，解决了轨道设计初值猜想问题，结合局部优化算法与多重打靶法对设计变量进一步迭代优化，重点分析了不同构型三体轨道与环月轨道对任务燃耗与飞行时间等关键指标的影响。研究表明：

1)针对特定的三体轨道，Halo与DRO的往返轨道特征点变轨增量、转移时间相近。随着环月轨道类倾角的增大，Halo转移速度增量逐步增大，而DRO转移呈现先增大后减小的趋势，转移时间降低。

2)针对Halo转移方案分析，不同环月轨道类倾角条件下，单程转移时间介于2～3.5天对应的速度增量在702.589～938.409 m/s范围内。当飞行时间差异在0.5天内时，选取大幅值Halo作为任务轨道，能够较好地降低往返转移速度增量。

3)针对DRO转移方案分析，不同类倾角工况下往返速度增量介于734.337～754.84 m/s，时间区间介于5.917～8.062天范围。相比于Halo转移方案，完成飞行任务的时间增加。

4)比较两者登月模型任务，Halo转移是综合考虑时间与燃耗的最佳转移方案，而DRO燃料最优转移适合于对时间要求不高的飞行任务。

上述设计方法与分析结论，对于考虑环月轨道与三体轨道间往返轨道设计及变量选取具有重要的参考价值。同时应注意，SQP算法为局部迭代优化算法，后续可进一步考虑全局优化算法对结果优化求解。