考虑结构参数不确定性的月球探测器结构优化设计
陈昭岳,刘 莉,岳振江
(北京理工大学宇航学院飞行器动力学与控制教育部重点实验室,北京 100081)
0 引 言
随着人类太空活动的深入开展,月球探测任务目标变得更加多样化,这对探测器的结构设计提出了更多要求。在探测器着陆过程中,探测器结构及其携带的有效载荷会受到短时冲击,为避免可能的结构功能失效,有必要在探测器结构设计之初,对探测器结构及其携带的重要有效载荷进行动力学响应分析,并基于其动力学特性进行结构优化设计。
目前,国内外研究者针对确定模型下的月球探测器结构特性优化开展了大量的工作。但用于优化的模型或是局部组件模型,或是复杂耗时的有限元模型,均无法实现探测器整体结构的快速优化。王亮[1]建立了太阳翼刚柔耦合模型,以展开收拢过程的加速度响应作为约束对腹板截面尺寸进行优化。文桂林等[2]建立了探测器非线性有限元模型并对着陆缓冲过程进行分析,并使用该模型对结构参数进行优化设计。董威利等[3]建立了月球探测器有限元模型,并引入脉冲子结构方法,建立了高效的探测器分析模型。陈树霖等[4]在文献[3]的基础上提出一种考虑结构动力学响应的优化设计流程,并对月球探测器太阳翼结构进行优化分析,获得了太阳翼结构设计参数。综上可以得出,要实现快速、精确的月球探测器整器模型优化需要对模型进行简化。
时域子结构主要包括有限元、模态和脉冲子结构三大类,其中已有大量针对有限元与模态子结构的研究。脉冲子结构方法(Impulse based substructuring method,IBS)于近年被提出,是一种高效求解且不损失精度的动态时域子结构方法[3]。Rixen[5]于2010 年首次提出了脉冲子结构方法的标准形式。之后,董威利等[6]将该方法成功应用于月球探测器着陆阶段动力学分析中,并对标准脉冲子结构方法的连接形式进行拓展。陈树霖等[7]发展了脉冲子结构与有限元及模态子结构间的复杂连接情况。综上可以看出采用子结构方法对模型进行部分简化建立多域子结构分析模型,根据组件性质将模型各组件建模为脉冲、模态和有限元子结构,最后完成整体模型的组装和求解分析,可以提高动力学求解效率。
探测器在生产设计和运行过程中会带来很多结构参数不确定性因素,且这些不确定性参数呈现空间分布特性,考虑结构参数不确定性影响的优化设计能更好的提高可靠性。相关学者对结构参数区间不确定性优化方法进行了一定的研究和应用。姜潮[8]提出了两种非线性区间数优化的数学转换模型,可以将最一般性的不确定性优化问题转换为确定性优化问题。吕辉等[9]利用基于区间分析旳不确定性优化方法对汽车制动器的稳定性进行了优化。刘钧圣等[10]等考虑区间不确定性因素对战术导弹总体参数的影响,开展了模块化战术导弹不确定性优化设计。Cheng等[11]提出了基于区间可靠性的结构设计优化模型。Cai等[12]提出了一种高效的不确定性优化目标函数求解方法,实现了多个不确定性参数的结构拓扑优化。上述方法虽然采用区间方法对不确定性建模,但是没有考虑参数不确定性的空间分布特性。
本文基于多域子结构综合方法和区间不确定性分析方法,提出了一种考虑区间不确定性的月球探测器结构优化框架。首先提出了月球探测器结构优化框架,建立月球探测器多域子结构模型,并介绍了基于区间可能度模型的区间不确定性优化方法;接着选取月球探测器着陆过程结构不确定性参数,开展探测器结构参数区间灵敏度分析得到关键影响参数;最后通过太阳翼和中心体隔板优化算例,验证了本节提出的优化框架可以有效应用到探测器结构的优化分析中,提高结构优化效率,指导探测器结构设计。
1 考虑结构参数区间不确定性的月球探测器结构动力学优化框架
1.1 月球探测器结构动力学不确定性优化框架
本节首先给出提出了月球探测器的结构动力学不确定性优化框架。优化框架中,优化目标选为月球探测器着陆过程的关键点冲击力学环境,约束条件包含设计变量约束和其他的性能约束。在优化框架中,优化过程分为两层嵌体优化,其中外层优化采用遗传算法用于设计变量寻优,内层通过区间方法计算不确定性目标函数和约束函数的区间,并通过转换后的目标函数求解设计变量的适应度。具体流程如下:
1)根据优化问题,确定优化的初始条件,包括设计变量、不确定参数及设计空间等。
2)根据优化对象、不确定性参数、模型来源等,构建或更新月球探测器多域子结构模型。
首先,将优化对象所在组件模型转换为有限元模型;其次,如果有相关联组件模型发生变化,例如对中心体部分结构进行优化,则原中心体模型被拆分,需对这些模型进行重新建模,并根据新模型转换脉冲或模态子结构模型;最后,分析子结构连接界面是否发生改变,完成新的多域子结构模型综合。
3)开始两层嵌体优化循环。
4)利用遗传算法产生结构优化变量的初始种群。
5)根据当前种群中选取一组当前设计变量值,带入内层不确定性分析,使用区间场方法对不确定性进行建模。
6)采用多域子结构综合模型,考虑当前不确定性设计变量,计算关注点的加速度响应谱区间和不确定性约束函数区间。
7)通过适应度函数计算当前设计变量的适应度。
8)重复步骤5)~步骤7),直至计算完成当前种群中所有个体的适应度,评估个体适应度。
9)遗传算法终止条件判断,如果满足收敛准则,结束优化,输出当前种群作为优化结果;如果不满足,则进行遗传算法的选择、交叉和变异运算,返回步骤4)。
考虑结构参数区间不确定性的月球探测器结构优化框架具体流程如图1所示。
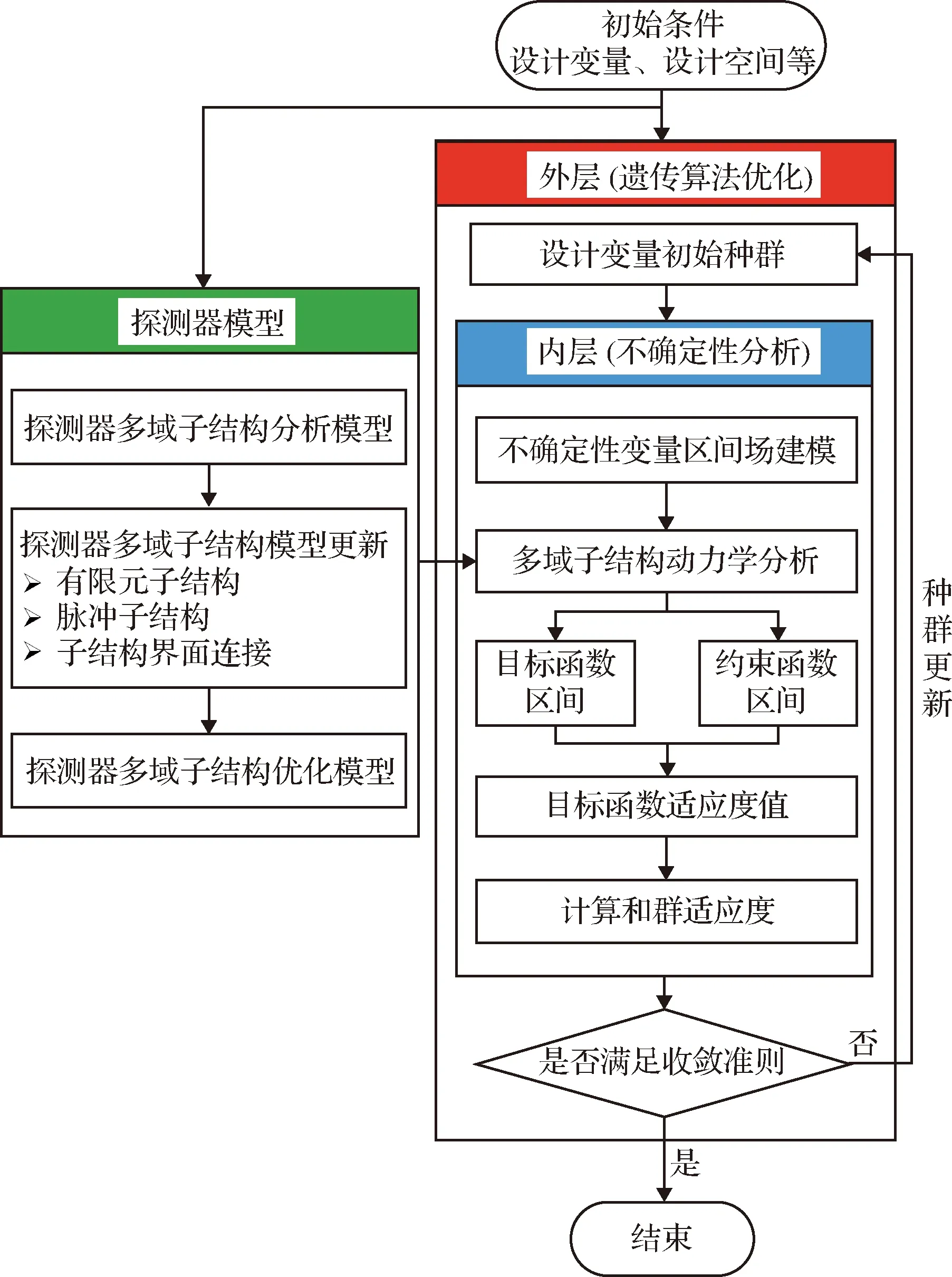
图1 考虑区间不确定性的月球探测器结构优化流程图Fig.1 Process of the dynamic optimum design of lunar lander under interval
1.2 月球探测器多域子结构模型
探测器不确定性分析和优化过程需要大量调用探测器分析模型,因此分析模型的计算效率尤为重要。本节首先建立了月球探测器有限元模型,随后基于多域子结构方法将部分组件转为模态或脉冲子结构,建立了月球探测器多域子结构模型,最后使用多域子结构运动综合方法,实现了探测器动力学的高效精确分析。
本文首先基于文献[13],建立月球探测器有限元模型。月球探测器由探测器中心体、着陆缓冲机构和有效载荷等部分组成,在有限元建模中只保留探测器中心体主结构、巡视器结构、太阳翼结构及着陆缓冲系统,探测器上其他有效载荷以等效质量形式分布到临近承力结构上。详细有限元建模过程参见文献[13]。此外,当月球着陆器按飞行程序进入着陆阶段,为了避免着陆冲击对太阳翼的损伤,太阳翼暂时收拢,因此建模中将太阳翼从展开状态转变为收拢状态,最终建立的探测器有限元模型如图2所示。
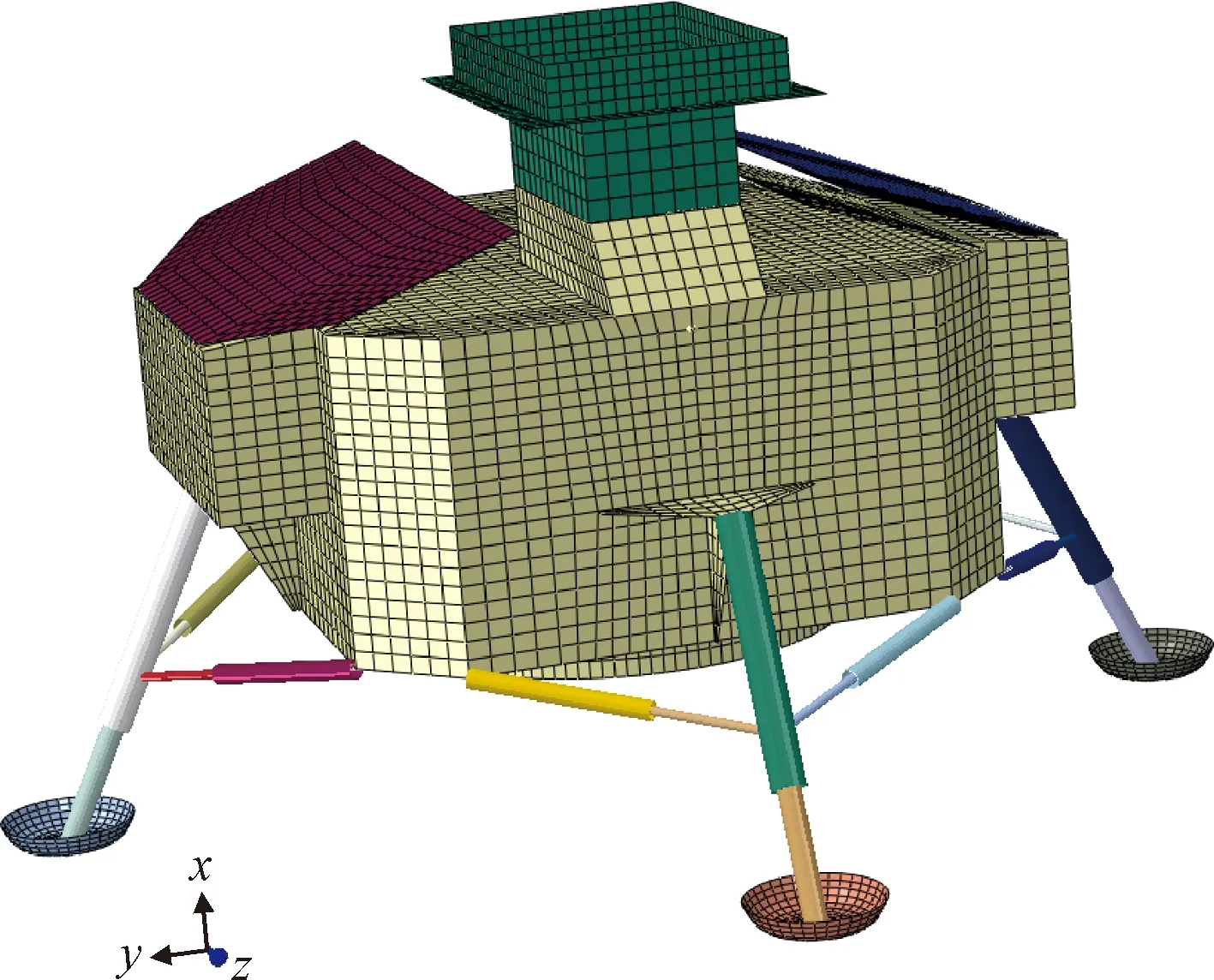
图2 月球探测器有限元模型[13]Fig.2 Finite element model of lunar lander
基于探测器有限元模型,根据各个有限元组件的动力学特性,建立月球探测器多域子结构模型,将探测器的部分组件由有限元子结构转换为模态子结构或脉冲子结构。
探测器动力学分析中,着陆缓冲机构的非线性有限元分析占用了大量的计算时间,因此应用多域子结构方法进行建模和分析中首先需要对着陆缓冲机构进行简化。当着陆姿态和角度固定时,由于探测器整体质量的变化相对于整体质量很小,因此可以将着陆过程的非线性因素简化为等效的激励载荷。首先通过探测器着陆冲击数值仿真测得缓冲机构产生的着陆缓冲载荷,接着计算着陆缓冲机构与中心体连接的12个连接点处的冲击载荷,最后根据反作用力原理,作用于探测器中心体上。计算冲击载荷的计算工况选取为探测器竖直着陆工况(着陆速度4 m/s、月球加速度g=1.63 m/s2),以+X+Y象限的主缓冲支柱为例,其传递给中心体的载荷时间历程曲线如图3所示。
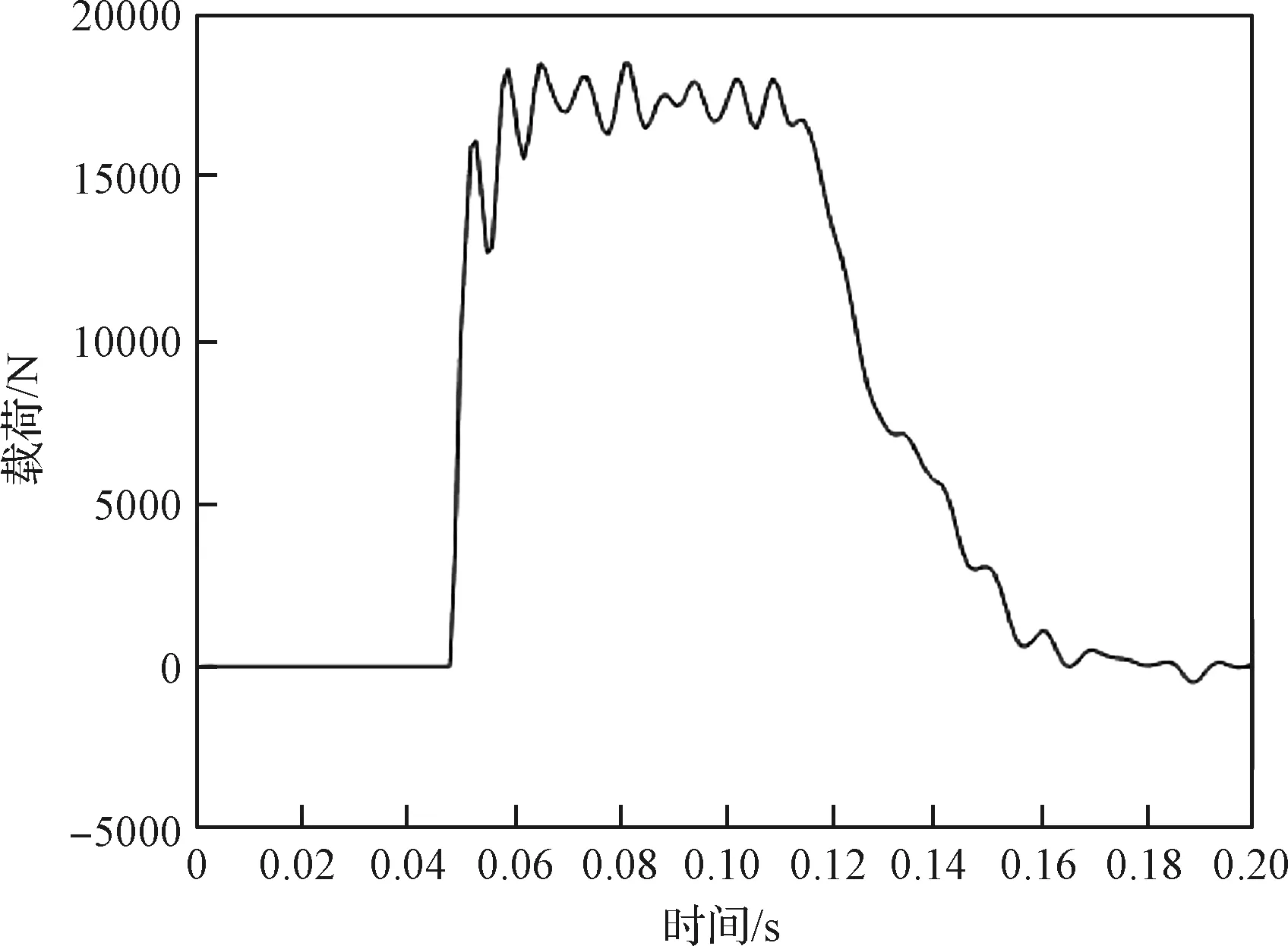
图3 着陆缓冲载荷Fig.3 Landing buffer load
探测器中心体有限元模型自由度众多(共87666个自由度),模态密集(1000 Hz内含2268阶模态),使用模态综合法将保留过多模态,且计算精度不能得到有效保证。同时中心体结构在后续分析中结构设计变化较小,因此可以使用脉冲子结构方法对探测器中心体建模,脉冲子结构模型中只保留输入输出自由度和连接界面自由度。将中心体划分为主体结构和中心体隔板结构。将中心体主体建为脉冲子结构。中心体主体与中心体隔板、着陆腿、巡视器和太阳翼分别有64、36、204和24 个连接自由度。减缩后的脉冲子结构自由度大幅减小,其中包括328个输入自由度(保留所有连接自由度)和293个输出自由度(连接自由度与中心点顶板纵向1个输出自由度)。
中心体隔板对中心体结构起加强作用,同时在设计时可能进行结构参数优化,因此将中心体隔板从中心体模型中拆分出来,建为有限元子结构,中心体隔板有限元子结构模型共有9576的自由度。
太阳翼在结构设计及建模中极有可能进行参数优化,迭代优化中需要重新建模,如果采用脉冲子结构对其建模,每一次的模型修改需要重新计算太阳翼的脉冲响应函数,这反而使得计算更为耗时,因此不适合将模型转换为脉冲子结构。同时与探测器中心体不同,太阳翼结构相对简单,包含的自由度较少,并且模态分布并不密集,适合采用模态子结构进行描述。因此将太阳翼有限元子结构模型转为模态子结构模型,对模型进行减缩,同时保留原有有限元子结构。未减缩的太阳翼有限元子结构共包含3024个自由度,减缩后的太阳翼模态子结构只保留41个自由度,模型计算规模大幅下降。
巡视器同样需要在结构设计及建模中进行参数优化,迭代优化中需要重新建模,因此不适合将模型转换为脉冲子结构。巡视器的模态密集,可以将巡视器的有限元子结构转换为模态子结构,对模型进行减缩,同时保留原有有限元子结构。未减缩的巡视器有限元子结构共包含7026个自由度,减缩后的太阳翼模态子结构只保留311个自由度,模型计算规模下降。
在月球探测器多域子结构模型中,太阳翼与中心体通过转轴铰链进行连接,在多域子结构模型综合中将连接形式简化为典型的刚-弹混合连接;巡视器和中心体通过Tie连接。通过以上分析,建立了探测器多域子结构动力学分析模型:探测器中心体为脉冲子结构,巡视器为模态子结构,太阳翼为有限元子结构,着陆缓冲载荷为系统激励。最终建立的多域子结构模型如图4所示,由于该模型在保证与有限元模型同等求解精度的前提下,极大的提高了求解效率,为探测器的动力学分析结构动力学优化提供了模型基础。
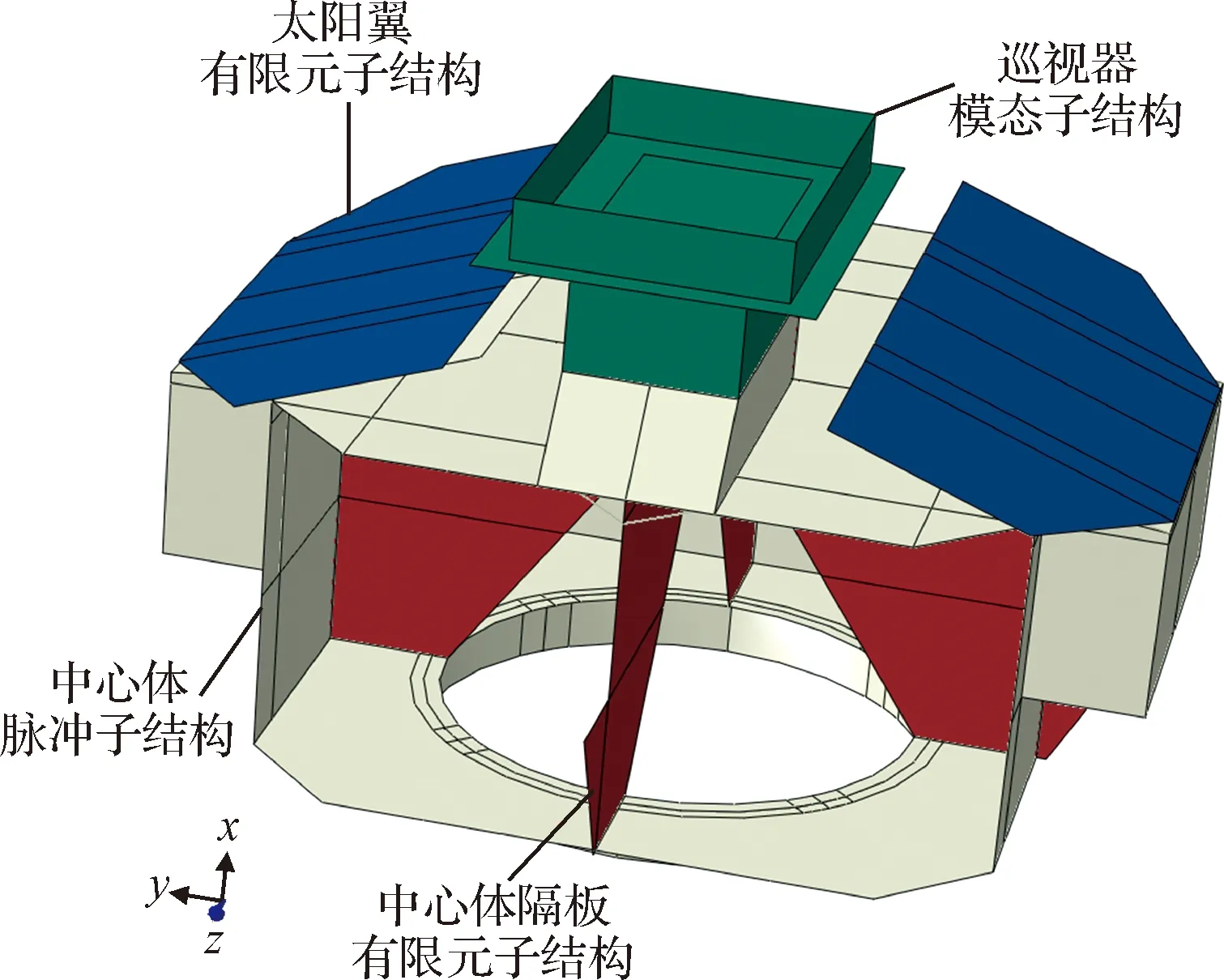
图4 探测器多域子结构模型Fig.4 Multi-domain substructure model of lunar lander
1.3 区间不确定性优化方法
传统的确定性优化问题中,优化模型中所有的参数都给以给定精确值,因此目标函数和约束在给定的设计变量点处可以计算出确定值。但实际工程问题中,很多参数存在不确定性,此时在设计点处,目标函数和约束函数均呈现不确定性,确定性优化问题转为不确定性优化问题。采用区间对设计参数建模并优化,即为区间不确定性优化方法。一般性的区间不确定性优化模型可表示为:
(1)
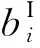
对于目标函数f(X,U),可以通过区间不确定性描述为:
f(X,U)∈fI(X)=[fL(X),fR(X)]
(2)
其中,目标函数的区间上下界可以通过区间分析方法如全局优化方法。
(3)
通过线性加权组合法处理目标函数的区间中点和区间半径,可以将不确定性目标函数转换为确定性的优化目标函数,并通过对确定性的目标函数进行评判,寻找最优设计变量。不确定性目标函数的线性加权组合法转换如式(4)所示:
β(fw(X)+ξ)/ψ
(4)
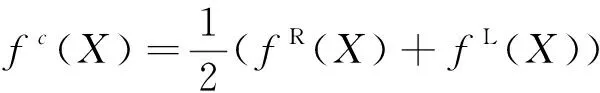
式中:0≤β≤1为多目标权重系数,为使fc(X)和fw(X)为非负数补偿系数,取较大的值来保证当不满足约束条件时设计变量受到惩罚;φ和ψ为标准化因子,其表达式如下:
(5)
解决不确定性优化问题的手段是通过一定的方法将该问题转化成确定性优化问题,这种转化方法需要借助转换模型,本节将介绍区间可能度方法用于处理带有区间不确定性变量的目标函数和约束[14]。
区间可能度方法假设两个区间为服从均匀分布的随机变量,通过计算随机变量的大小关系的概率来获得区间比较关系的可能度,文献[8]给出了完备的区间可能度模型,对于任意两个区间AI和BI,它们共有6种可能的位置关系,根据可能的位置关系,可以给出可能度模型的计算公式,如式(6)所示:
(6)
基于可能度模型,式(1)中不确定性约束函数,可以转换成如下的确定性不等式约束:
(7)
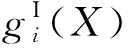
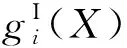
经过线性加权组合法和可能度模型的转换,原不确定性优化问题转化为确定性多目标优化问题:
(8)
可以通过罚函数的方法来处理式中的约束条件,使其转化为无约束优化问题:
(9)
式中:σ为惩罚因子,取较大的值来保证当不满足约束条件时设计变量受到惩罚,使得寻优继续进行。
至此,对于一般性的非线性区间优化问题经过转换变成可以采用传统优化手段解决的单目标无约束确定性优化问题。
2 考虑区间不确定性的月球参数灵敏度分析
2.1 区间不确定性灵敏度分析方法
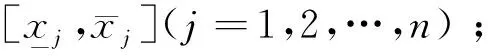
(10)
其中:θij(i=1,2,…,m;j=1,2,…,n)为第j个模型参数对第i个决策目标的综合影响因子。
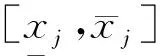
令:
(11)
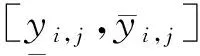
(12)
敏感性因子矩阵的列向量表征了同一个不确定性输入参数对不同的决策目标yi的影响程度;敏感性因子矩阵的行向量表征了不同的不确定性输入参数xj对同一个的决策目标的影响程度。
由于各模型参数的量纲往往不尽相同,在参数敏感性分析过程中需要对各个参数的不确定性进行归一化处理,定义参数XI的区间变异系数为δ=ΔX/Xc,文献[13]指出随着参数区间变异系数的不同,获得的参数对决策目标的敏感性因子是不同的。在进行参数敏感性分析时,应将参数区间取为参数在相同变异系数下的变化区间。
2.2 月球探测器不确定性参数灵敏度分析
为了较为全面的考虑月球探测器结构阻尼、连接刚度、结构尺寸和材料特性等参数的不确定性影响,本文分别选取结构阻尼、巡视器顶板铺层厚度、中心体隔板铺层厚度、太阳翼铺层厚度、巡视器顶板材料刚度、中心体隔板材料刚度、太阳翼材料刚度和太阳翼连接扭转刚度等8个参数作为分析对象,对月球探测器软着陆过程的冲击力学环境进行不确定性参数灵敏度区间分析。各个参数的变异系数均取为0.1,即10%的不确定性区间,选取的参数和不确定性区间见表1。
首先,考虑全部不确定性参数,通过区间场方法完成参数不确定性建模,同时采用多域子结构综合方法提高分析效率,计算巡视器、中心体和太阳翼特征点处冲击响应谱峰值的不确定性区间,并作为全参数不确定性影响下的决策目标可行域区间用于后续分析,见表2。
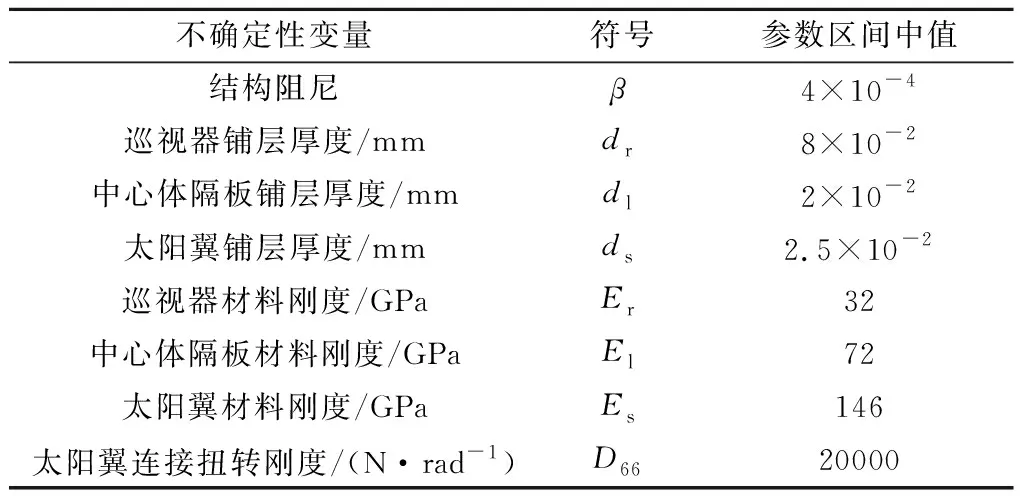
表1 模型不确定性因素Table 1 Uncertain parameters of lunar lander

表2 决策目标的可行域区间Table 2 Uncertain range of dynamic response
可以看出,当输入参数的不确定性区间变异系数取为0.1时,中心体响应谱峰值的区间相对较小,可行域半径仅为0.034,输出响应相对于输入响应的不确定性减小,这是由于中心体结构相对复杂,内部有大量的局部加强结构降低了整体的动力学响应。而巡视器和太阳翼的输出结果不确定性区间均有所增大,分别为0.154和0.0203,因此当考虑参数不确定性时,有必要对巡视器和太阳翼的输出结果不确定性进行重点关注。
对每一个不确定性参数的灵敏度进行分析计算,单独考虑一个不确定性参数计算得到三个测点的响应谱区间,根据求得模型参数对决策目标的敏感性因子矩阵如下:

(13)
为了更直观地比较各参数灵敏度,绘制决策目标对各不确定性参数的灵敏度柱状图,如图5所示。
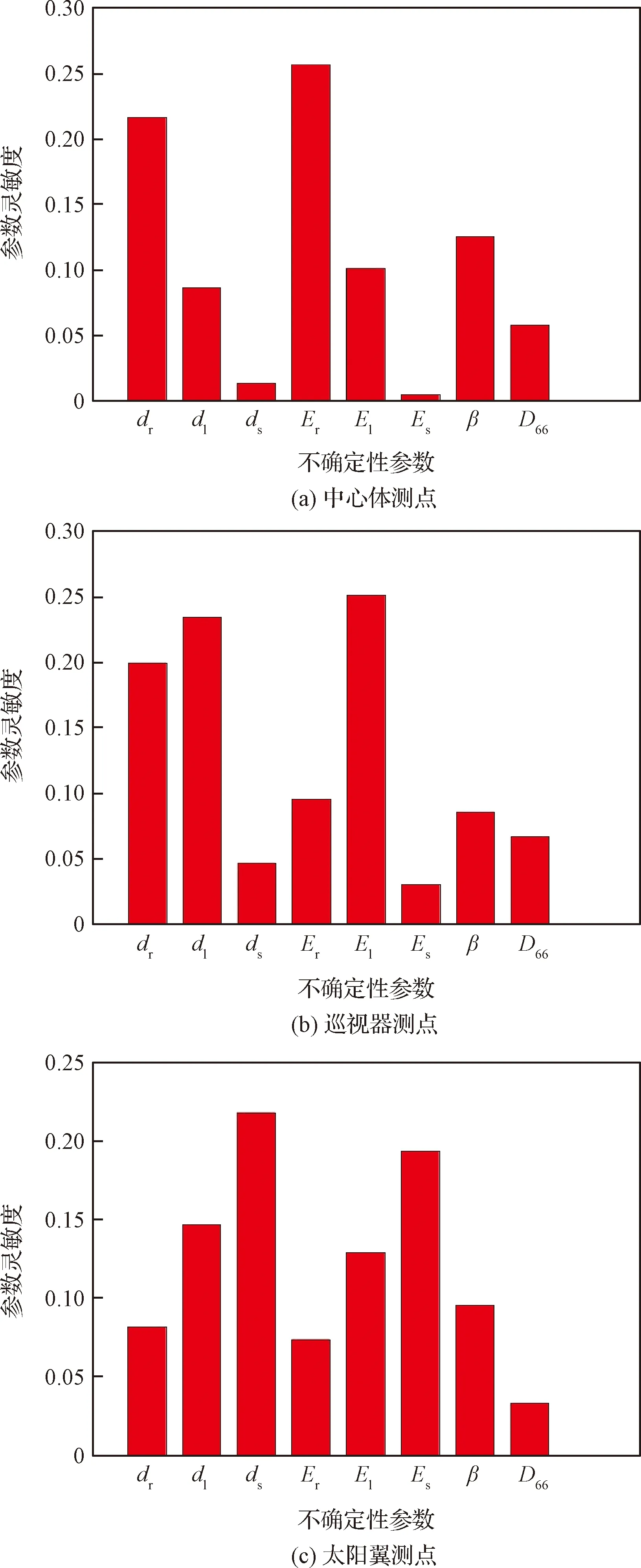
图5 不确定性参数灵敏度分析结果Fig.5 Interval sensity of lunar lander parameters
由图5和式(13)可知:
1)三个结构测点的力学环境对结构阻尼β和连接扭转刚度D66的灵敏度分析结果总体趋势基本相同,其中结构阻尼对测点的影响因素相对更大,三个结构对连接扭转刚度的灵敏度均在0.05以下。
2)对于巡视器、太阳翼和中心体三个结构,灵敏度最大的不确定性变量分别为所在结构的弹性模量和结构厚度,这与直观的物理印象相同。值得注意的是,中心体测点的灵敏度结果中,巡视器弹性模量和结构厚度的灵敏度要远大于太阳翼结构的弹性模量和结构厚度灵敏度,这表明巡视器对中心体响应的影响要更大,在后续对巡视器结构的优化设计分析中要注意其对中心体响应的影响。中心体的结构参数对巡视器和太阳翼结构响应均有较大的影响。
3)太阳翼的结构质量远小于中心体和巡视器,因此这两个结构对太阳翼结构弹性模量和结构厚度灵敏度极小,在对太阳翼的结构分析中可以减小对这两个结构的顾虑。
综上所述,在探测器着陆力学环境分析中,由于结构弹性模量和结构厚度对结果有很大影响,应当提高这两种不确定性因素的准确度。
3 数值算例
本节分别以太阳翼和中心体隔板结构为例,采用本文提出的不确定性优化设计框架,开展相应的结构优化设计,来说明框架的具体使用方法,并对框架的有效性进行验证。
3.1 月球探测器太阳翼结构优化设计实例
太阳翼结构作为探测器工作动力的来源,成为月球探测器最重要的组成之一。当月球探测器着陆过程中,其冲击载荷将对太阳翼产生一定的冲击。
本节以太阳翼为例,将太阳翼重要位置处的动力学环境作为优化目标,考虑太阳翼的材料杨氏模量、系统结构阻尼、中心体隔板杨氏模量为不确定性变量,对太阳翼结构进行不确定性优化,从而改善其关键位置的力学环境条件。
3.1.1月球探测器太阳翼结构优化设计模型
本算例中需要优化的结构为太阳翼,根据优化框架,首先给出探测器分析模型的选择,将太阳翼和中心体隔板建为有限元模型,巡视器和中心体结构建立为脉冲子结构,巡视器只保留与中心体的连接自由度,共240个自由度,中心体只保留与巡视器、中心体隔板和太阳翼的连接自由度,以及外力输入自由度,共3328个输入自由度,293个输出自由度。结构优化模型如图4所示。
太阳翼结构优化分析中,太阳翼的材料杨氏模量、系统结构阻尼、中心体隔板杨氏模量为不确定性变量,不确定性参数的取值见表3。
本节给出太阳翼结构动力学优化的数学模型设计优化三要素选择,即优化目标、约束条件和设计变量,并最终提出太阳翼结构动力学优化数学模型。
1)优化目标
本算例的优化目标是太阳翼着陆冲击力学环境,使得太阳翼特征点处的冲击力学环境最小,保证太阳翼结构及有效载荷的安全性。在探测器着陆冲击力学环境分析中,使用加速度冲击响应谱对探测器部组件处的冲击力学环境进行量化[17-18]。通过响应谱不确定性分析得到太阳翼特征点加速度响应谱最大值的区间,并通过式(4)转换为确定性优化目标函数,最终优化目标函数如式(14)所示:
β(fw(U)+ξ)/ψ
(14)

表3 模型不确定性因素Table 3 Range of uncertain parameter
其中:U为目标优化结构特征点加速度响应;f(U)为转换后的目标优化结构特征点位置加速度冲击响应包络谱峰值。
2) 约束条件
在考虑不确定性的结构优化方法中,约束条件的选择要考虑多个因素,包括太阳翼的质量特性要求、动响应要求及结构固有频率要求,巡视器的力学环境要求。约束条件的选取同时要考虑确定性约束条件和不确定性约束条件。综合考虑后给出了优化的约束条件:
①质量特性要求:为了能够携带更多的有效载荷,探测器结构的总质量应尽可能轻,对太阳翼结构总质量Ms提出了质量指标要求:Ms≤Msmax=4.5 kg。
②太阳翼动响应位移:为了避免太阳翼结构由于冲击载荷作用发生振动,与探测器本体碰撞,太阳翼角点处相对位移ds应在可控范围之内:ds≤dsmax=40 mm。
③太阳翼响应谱峰值最大值,为保证太阳翼结构的安全可靠,太阳翼响应谱峰值最大值应满足最大响应谱限制:f(U)≤3500 m/s2。
④巡视器力学环境:由于材料存在不确定性,探测器着陆响应相对于确定性响应可视为不确定性区间Ar,巡视器力学环境满足区间限制:Ar⊆kI。
3) 设计变量
太阳翼作为探测器的主要供能装置,其几何尺寸由板上的电池片决定,所以在结构动力学优化设计中不涉及其几何外形参数。基于灵敏度分析结果,太阳翼碳纤维铺层厚度对太阳翼结构刚度、强度影响显著,因此将太阳翼碳纤维铺层厚度选为优化设计变量;太阳翼整体刚度同时受到太阳翼与本体间连接铰链扭转刚度的影响,因此同时对一次扭转刚度进行优化。综合以上分析,设计变量及设计空间见表4。

表4 太阳翼结构动力学优化设计变量Table 4 Dynamic optimum design variables of solar wings
通过以上对优化三要素:优化目标、约束条件、设计变量的分析,太阳翼结构动力学优化问题可描述为标准优化数学模型:
(15)
3.1.2月球探测器太阳翼结构优化结果与分析
采用本文给出的优化流程进行优化设计。相关参数设置如下:优化算法参数ξ为0,β为0.5,罚因子σ为10000,正则化因子φ和φ分别取1.33和0.34;外层遗传算法的种群规模设为30,最大代数为50,交叉概率为0.6,变异概率为0.1;不确定性约束kI=[550,750]m/s2,可能度λ取为0.6。
1)不确定性优化收敛性分析与结果分析
首先对优化流程的收敛性进行分析,优化流程中外层遗传算法的种群适应度随种群代数的变化曲线如图6所示。根据适应度收敛曲线,当种群代数达到40代时,种群适应度基本收敛。
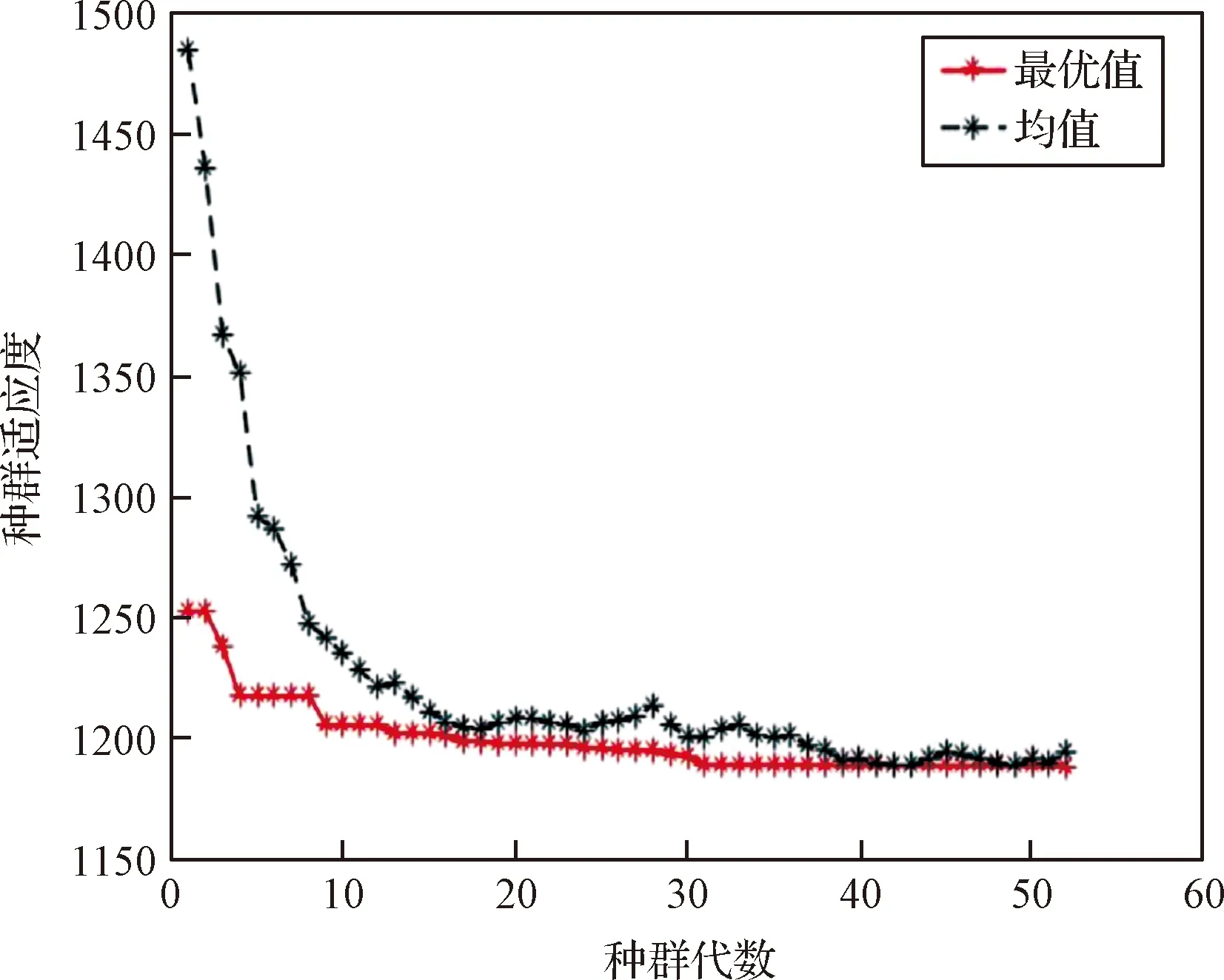
图6 种群适应度收敛曲线Fig.6 Iterative convergence curve of fitness value
经过优化求解,得到优化后的设计变量,不确定性优化后的设计变量与初始变量的对比结果见表5。

表5 优化前后设计变量取值Table 5 The design variables before and after the optimization
根据设计变量优化结果,优化后的太阳翼厚度ts和扭转连接处刚度系数D66相比优化前的取值有大幅增加,其中太阳翼厚度增加71.2 %,扭转刚度系数增加 48.5%。
经过优化后的着陆冲击力学环境、结构动力学系数、结构质量与结构初始状态的对比结果见表6。
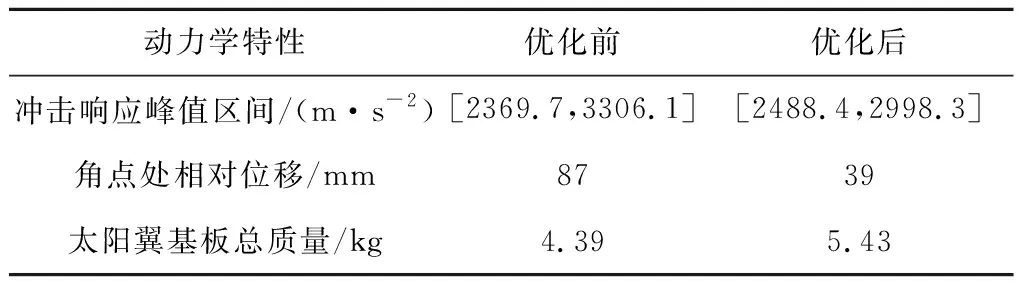
表6 优化前后动力学特性对比Table 6 The structural dynamic performance before and after the optimization
通过对比优化前后着陆力学环境,可以发现经过优化后,冲击响应峰值区间变小,区间上界和区间半径都略有降低;太阳翼角点相对最大位移满足约束要求,总质量在满足约束要求前提下略有增加,分析结果表明优化后的着陆冲击力学环境得到有效改善。
2)可能度影响分析
在保证优化流程中结构参数和优化算法参数设置不变的前提下,可能度λ分别选取0、0.3、0.6和1,比较不同可能度水平下太阳翼冲击响应谱和设计变量的优化结果,优化结果见表7。
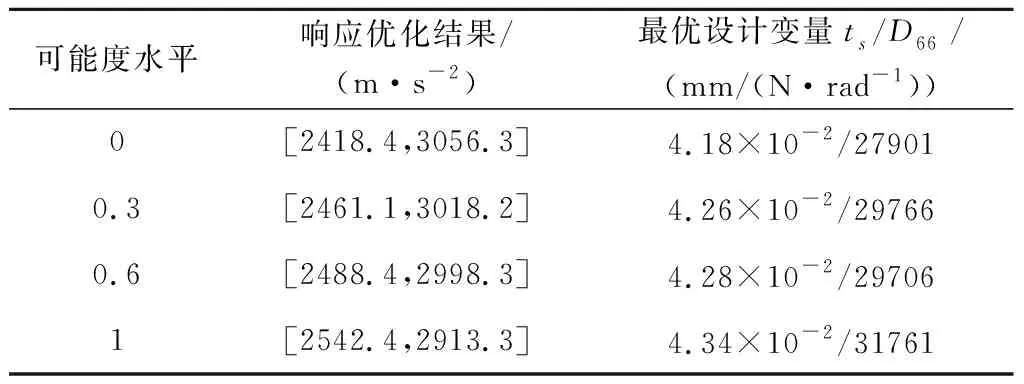
表7 不同可能度水平太阳翼不确定性优化结果Table 7 Optimization result of solar wings under interval degree
对比结果表明,随着可能度的增大,响应优化结果中太阳翼厚度ts和扭转连接处刚度系数D66随之增加,太阳翼的响应谱区间减小,整体设计趋向保守。
可能度水平代表了决策者对可靠性的要求,决策者对优化结果的可靠性要求越高,对约束函数区间的要求越小,则应选取较大的可能度水平。在本次优化中,不确定性约束选取为巡视器冲击响应谱区间,当可能度水平较高时,表示设计者对巡视器力学环境的关注程度较高,相应的对太阳翼的关注降低,因此设计变量优化结果相对较小,响应谱区间增大。
3)不确定性优化与确定性优化对比分析
忽略不确定性因素的影响,采用传统的遗传算法对太阳翼力学环境进行优化,并与不确定性优化结果对比。确定性优化的分析模型、设计变量与不确定性优化相同。优化设计变量仍选取为太阳翼单层碳纤维厚度和扭转刚度系数,设计空间的上下限也保持不变。忽略结构阻尼、中心体隔板材料杨氏模量和太阳翼材料杨氏模型的不确定性因素,整体结构不考虑不确定性。
确定性优化的优化目标为使太阳翼特征点处的响应谱峰值最小,优化目标如式(16)所示:
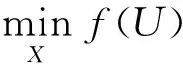
(16)
确定性优化的约束条件只保留对质量特性、太阳翼响应谱峰值最大值和太阳翼动响应相对位移的约束,忽略对中心体力学环境的约束,即:
①质量特性要求:为了能够携带更多的有效载荷,探测器结构的总质量应尽可能轻,对太阳翼结构总质量Ms提出了质量指标要求:Ms≤Msmax=4.5 kg。
②太阳翼动响应位移:为了避免太阳翼结构由于冲击载荷作用发生振动,与探测器本体碰撞,太阳翼角点处相对位移ds应在可控范围之内:ds≤dsmax=40 mm。
③太阳翼响应谱峰值最大值,为保证太阳翼结构的安全可靠,太阳翼响应谱峰值最大值应满足最大响应谱限制:f(U)≤3500 m/s2。
最终给出确定性优化数学模型如式(17)所示:
(17)
将确定性优化结果与可能度水平为0.6的不确定性优化结果对比,其中冲击响应谱峰值对比中,不确定性优化结果选取太阳翼冲击响应谱区间上界。对比结果见表8。
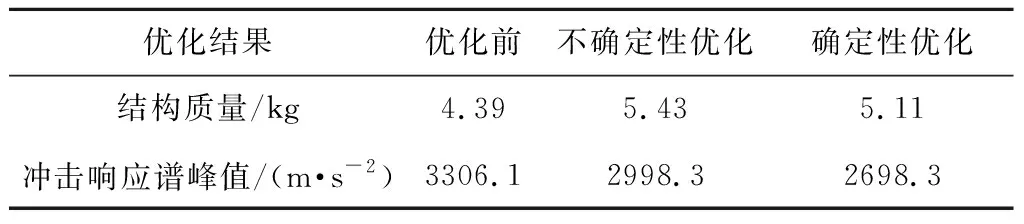
表8 确定性优化与不确定性优化结果对比Table 8 Comparasion between deterministic and uncertain optimizatoin
对比结果表明:相比于确定性优化结构,不确定性优化中太阳翼结构质量增重较多,响应谱峰值降低的较小,整体的优化结果更为保守。这是因为不确定性优化方法在优化过程中考虑了材料、载荷的不确定性对动力学响应的影响,同时在分析中考虑了特别的恶劣工况,因此不确定性分析结构对结构承载能力提升较多,优化结果更具可靠性。
在优化过程中,外层GA算法共调用内层优化模型1530次,每次内层优化要调用模型分析2次,如果采用全阶有限元模型,单次模型调用时间约1400 s,而使用本文提出的多域子结构方法,分析耗时约190 s,分析效率大幅提高。同时基于区间场分析方法,建立代理模型也大幅提高了分析效率。
3.2 月球探测器中心体隔板结构优化设计
探测器中心体承载了大部分探测任务仪器,并焊接燃料贮箱,是月球探测器的重要组件之一。在月球探测器着陆过程中,中心体将承受冲击载荷。中心体隔板作为中心体的加强结构,为中心体提供了主要支撑和传力作用,因此对中心体隔板的结构优化具有重大意义。
本节以中心体隔板为例,将中心体重要位置处的动力学环境作为优化目标,考虑中心体隔板材料杨氏模型、系统结构阻尼、巡视器隔板杨氏模型和隔板厚度为不确定性变量,对中心体隔板结构进行不确定性优化,从而改善中心体结构的力学环境条件。
3.2.1月球探测器中心体隔板结构优化设计模型
本算例中需要优化的结构为中心体隔板,根据优化框架,首先给出探测器分析模型的选择,将太阳翼、巡视器和中心体隔板建为有限元模型,中心体结构建立为脉冲子结构,只保留外力输入自由度,以及与巡视器、中心体隔板和太阳翼的连接自由度,结构优化模型如图4所示。
中心体隔板的结构优化分析中,中心体隔板材料杨氏模型、系统结构阻尼、巡视器隔板杨氏模型和隔板厚度为不确定性变量,不确定性参数的取值见表9。
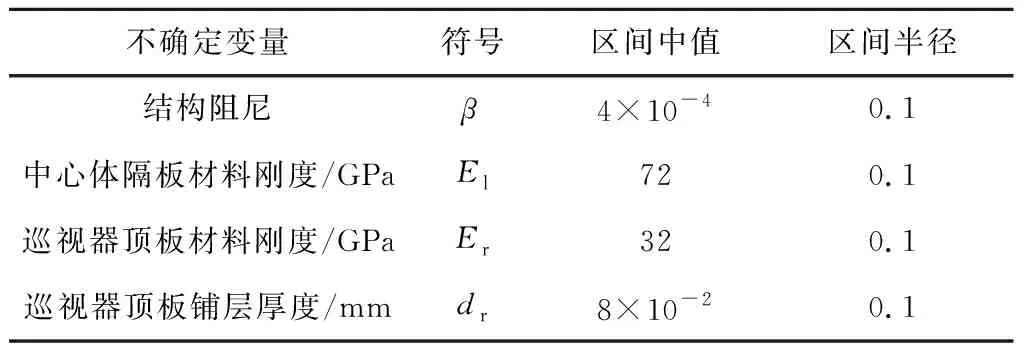
表9 模型不确定性因素Table 9 Range of uncertain parameter
本节给出中心体隔板结构动力学优化的数学模型的设计的优化三要素的选择,即优化目标、约束条件和设计变量,并最终提出中心体隔板结构动力学优化数学模型。
1)优化目标
本算例的优化目标是中心体结构的着陆冲击力学环境,使得中心体特征点处的冲击力学环境最小,保证中心体结构及有效载荷在动态冲击过程中结构性能完好。
在探测器着陆冲击力学环境分析中,使用加速度冲击响应谱对探测器部组件处的冲击力学环境进行量化,通过响应谱不确定性分析得到中心体特征点加速度响应谱最大值的区间,并转换为确定性优化目标函数,最终优化目标函数如式(18)所示:
β(fw(U)+ξ)/ψ
(18)
2)约束条件
在考虑不确定性的结构优化方法中,约束条件的选择要考虑多个因素,包括中心体的质量特性要求、动响应要求及结构固有频率要求,巡视器的力学环境要求。约束条件的选取同时要考虑确定性约束条件和不确定性约束条件。综合考虑后给出了优化的约束条件:
①质量特性要求:为了能够携带更多的有效载荷,探测器结构的总质量应尽可能轻,对太阳翼结构总质量Ml提出了质量指标要求:Ml≤Mlmax=25 kg。
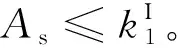
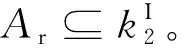
3) 设计变量
中心体隔板作为中心体的支撑结构,其几何尺寸受到中心体模型的限制,因此在结构动力学优化设计中不涉及其几何外形参数。基于灵敏度分析结果,中心体隔板的厚度对中心体响应影响显著,因此设计变量及设计空间见表10。

表10 中心体隔板结构动力学优化设计变量Table 10 Dynamic optimum design variables of solar wings
通过以上对优化三要素:优化目标、约束条件、设计变量的分析,太阳翼结构动力学优化问题可描述为标准优化数学模型:
(19)
3.2.2月球探测器中心体隔板优化结果与分析
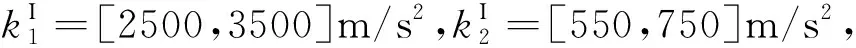
首先对优化流程的收敛性进行分析,优化流程中外层遗传算法的种群适应度随种群代数的变化曲线如图7所示。根据适应度收敛曲线,当种群代数达到40代时,种群适应度基本收敛。
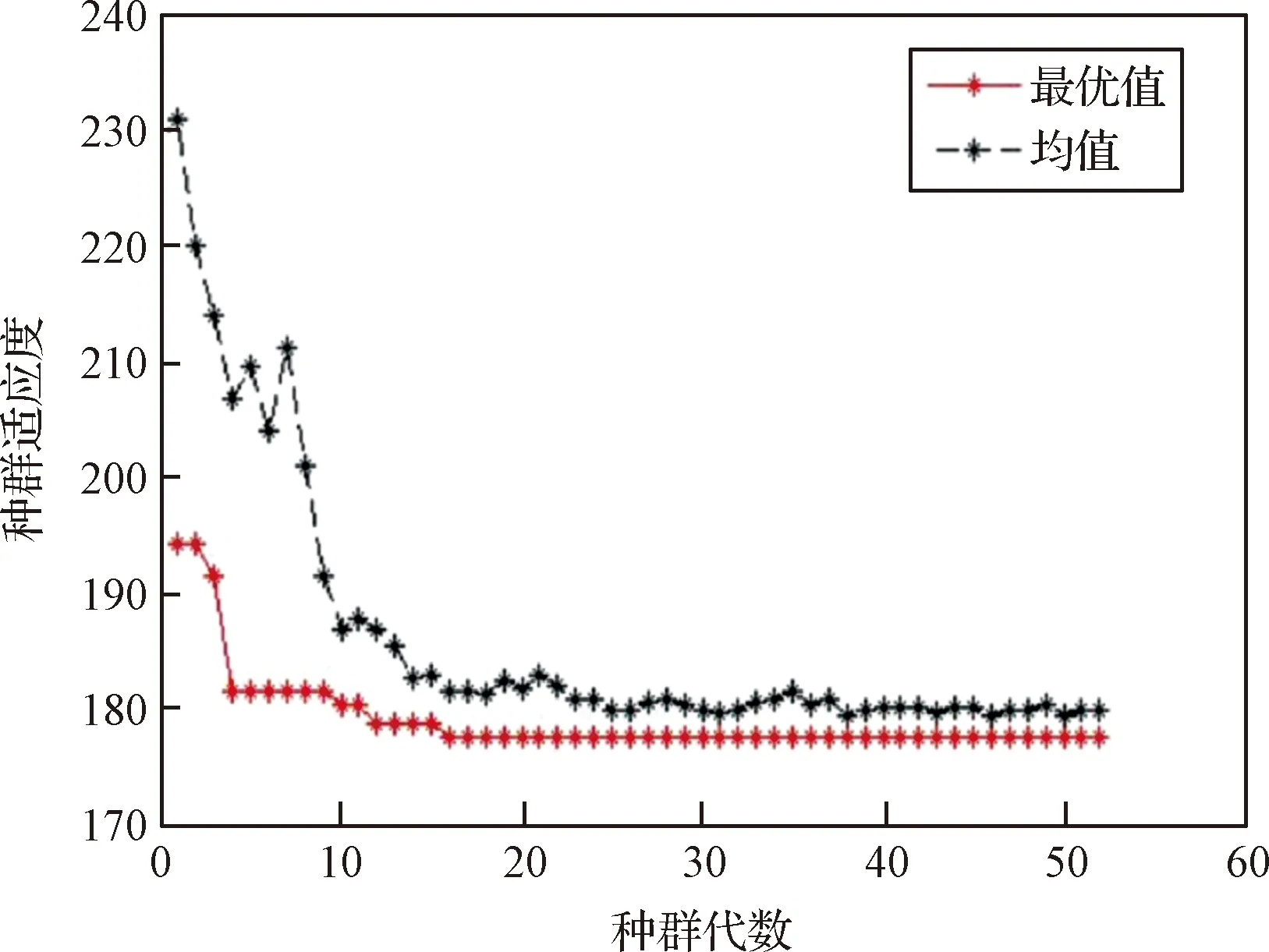
图7 种群适应度收敛曲线Fig.7 Iterative convergence curve of fitness value
不确定性优化后的设计变量与初始变量的对比结果见表11。

表11 优化前后设计变量取值Table 11 The design variables before and after the optimization
根据设计变量优化结果,优化后的中心体隔板厚度tl相比优化前的取值有大幅增加,中心体隔板厚度增加44.7 %。
经过优化后的着陆冲击力学环境、结构动力学系数、结构质量与结构初始状态的对比结果见表12。

表12 优化前后动力学特性对比Table 12 The structural dynamic performance before and after the optimization
通过对比优化前后着陆力学环境,可以发现经过优化后,冲击响应峰值区间上下界均有所减小,同时冲击响应峰值区间半径也降低,整体的着陆冲击力学环境得到有效改善。总质量在满足约束要求前提下略有增加,分析结果表明优化后的着陆冲击力学环境得到有效改善。
4 结 论
针对月球探测器结构优化过程中优化效率和参数不确定性影响的问题,本文引入多域子结构综合方法和区间不确定性分析方法,提出了考虑结构参数区间不确定性的月球探测器结构性优化框架。得到如下结论:
1)本文提出优化框架采用多域子结构模型作为优化模型,优化效率相比传统有限元优化模型,使得优化过程单次动力学分析效率提高10倍以上,显著缩减了结构动响应计算耗时。
2)通过太阳翼和中心体隔板优化算例证明,本文提出的优化框架在优化过程中能够考虑结构参数不确定性。不确定性优化结果的区间中值与确定性优化结果相近,同时不确定性优化结果考虑了最恶劣的结构工况,优化结果能够保证结构的可靠性。
3)相比传统优化中,更改优化目标即需要整体模型重新建模,本文提出的优化框架可以灵活的根据优化对像建立优化模型,降低了模型更新的耗时,能够快速进行结构优化设计。

