航天器零推进剂姿态机动启发式规划方法
王 卓,徐 瑞,李朝玉,朱圣英,陈德相
(1. 北京理工大学宇航学院,北京 100081;2. 深空自主导航与控制工业和信息部重点实验室,北京 100081;3.上海卫星工程研究所,上海 200240)
0 引 言
随着航天技术的发展,需要航天器具有良好的姿态机动能力,而航天器的姿态机动能力在很大程度上取决于姿态执行机构的能力[1]。航天器在完成姿态机动任务时,大多采用推力器作为姿态执行机构。然而,采用推力器进行长周期大角度的姿态机动会消耗大量燃料,在一定程度上限制了航天器的工作能力。零推进剂姿态机动(Zero propellant maneuver, ZPM)技术是一种成功应用于国际空间站的大角度姿态机动技术[2]。ZPM采用控制力矩陀螺代替推力器作为姿态执行机构,这在延长航天器在轨时间,提高航天器安全性方面具有实际意义[3]。
ZPM的概念最早出现于1996年,由美国麻省理工学院德拉普尔实验室的Bedrossian提出[4]。其核心思想是提前规划出满足控制力矩陀螺约束的姿态路径和控制力矩陀螺框架角运动路径,使得航天器在执行多种空间任务时控制力矩陀螺不会陷入奇异或饱和状态,从而不需要消耗额外燃料进行姿态机动或消除控制力矩陀螺的奇异和饱和状态,进而实现航天器的零推进剂姿态机动。
2006年11月5日,NASA首次在国际空间站上采用ZPM技术完成了90°的大角度姿态机动,使用双框架控制力矩陀螺作为姿态执行机构[5]。2007年3月3日,NASA在国际空间站上通过ZPM技术实现180°的大角度姿态机动,和同等机动条件下的推力器相比节省50.76 kg燃料消耗,节约的燃料成本达110万美元[6]。同时,预计于2022年完成的中国空间站,采用的执行机构是可靠性高和可控性好的单框架控制力矩陀螺(Single gimbal control moment gyroscopes,SGCMGs)[7]。上述工程实验为本文的研究提供了方向和理论依据,但是其考虑的约束较少,而实际的航天器大角度姿态机动不仅要考虑控制力矩陀螺的约束,更要考虑姿态约束。
当前的SGCMGs的研究,大多基于给定参考姿态机动路径的SGCMGs奇异躲避或逃离操纵律设计[8-10]。Kurokawa使用梯度法避免SGCMGs奇异,将零运动添加到伪逆解中得SGCMGs奇异避免操纵律,但是这种方法可能会陷入某些特殊的奇异状态[11]。Bedrossian等提出了基于力矩误差的奇异鲁棒操纵律,可以让SGCMGs在陷入奇异时快速逃离奇异,但是当控制力矩矢量和奇异方向一致时,就会陷入锁死状态从而无法逃离奇异[12]。Hou等提出了一种解析的SGCMGs奇异躲避操纵律,在满足系统性能指标的同时实现全局奇异躲避[13]。上述方法可以跟踪设定好的参考姿态路径进行奇异躲避,但是实际运行中的航天器姿态路径难以提前确定,且航天器难以实时更新姿态路径参数。因此,虽然上述方法可以有效避免SGCMGs奇异,但并不适合解决实际航天器运行中的ZPM问题。
针对ZPM问题,在设计SGCMGs奇异躲避操纵律的同时,也要对航天器的姿态机动进行规划[14-16]。NASA的Bedrossian等通过伪谱法进行ZPM技术的研究,借助DIDO优化软件设计出国际空间站首次ZPM大角度姿态机动的路径轨迹[2]。Zhang等采用高斯伪谱法得出最优的姿态机动路径和SGCMGs框架角运动,能够使SGCMGs在ZPM机动中一直远离奇异状态[17]。但是通过伪谱法仿真可以发现,该方法的计算时间过长且无法满足节点间约束。为了实现时间和能量等多种指标优化,Zhao等提出了伪谱法和物理规划相结合的混合算法,实现了ZPM中SGCMGs框架角运动的多目标优化,但也只能生成无姿态约束的机动路径[18]。以往的研究一般只考虑ZPM过程中的SGCMGs约束和初始边界约束,而忽略了姿态空间约束,如太阳能电池板和光学敏感器的方位约束[19]。同时,大多数ZPM规划方法通过伪谱法和优化工具箱进行全局离线规划,难以实现在轨应用,因此需要研究考虑满足多种约束的在线ZPM规划方法。
基于上述讨论,本文主要研究航天器姿态机动过程中的ZPM技术,旨在提出一种同时考虑姿态约束和SGCMGs约束的ZPM路径规划方法,使航天器在进行姿态机动前可以规划出一条满足多种约束的姿态机动路径和SGCMGs框架角路径。本文提出一种基于约束评价启发式的差分进化(Differential evolution,DE)方法,通过对ZPM原理进行约束和复杂度分析,设计姿态规划空间内的ZPM规划序列,采用欧拉机动保证路径的连续性。在规划空间中建立约束评价函数,设计基于评价函数的启发式策略,对航天器约束和控制力矩陀螺约束进行解耦处理。将约束评价启发式策略用于改进DE算法的种群变异,引导ZPM规划序列满足约束。最后通过航天器ZPM仿真校验,验证启发式DE方法的合理性和有效性。
1 航天器零推进剂姿态机动模型
本节对航天器ZPM进行建模和约束分析,并且定义了新的SGCMGs饱和度量。
1.1 ZPM动力学
本文将航天器视为能够三轴运动的刚体,在绕中心天体转动的同时可以自由机动[14],并以SGCMGs为姿态执行机构,选择姿态四元数作为姿态参数,ZPM的姿态运动学和动力学方程如下:
(1)
(2)
式中:姿态四元数q=[q0,q1,q2,q3]T,且满足:
(3)
其中:uc表示SGCMGs提供的控制力矩;Te表示环境力矩;J是航天器的惯性矩阵;ω0表示航天器的轨道角速度;ω=[ω1,ω2,ω3]T表示航天器角速度,ω+是ω的叉乘矩阵形式:
(4)
在ZPM中需要考虑SGCMGs框架角运动,SGCMGs的动力学方程为:
(5)
(6)
式中:hc表示SGCMGs角动量;h0表示单个SGCMG的角动量;δ表示SGCMGs框架角组合;Jc(δ)表示SGCMGs控制力矩的雅克比矩阵:
Jc(δ)=ACδ-BSδ
(7)
式中:A和B是SGCMGs的安装矩阵,与SGCMGs的构型相关;Sδ是框架角组合的正弦对角矩阵;Cδ是框架角组合的余弦对角矩阵。
1.2 SGCMGs约束
实现ZPM的关键是机动过程中SGCMGs满足奇异和饱和约束,这里对SGCMGs约束进行分析。
单个SGCMG只能产生垂直于框架轴的角动量,因此只能提供单自由度的控制力矩。为了实现航天器的三轴控制,至少需要三个及以上SGCMG提供控制力矩[18]。由于可靠性高和控制性能较好,本文采用五棱锥构型的SGCMGs,如图1所示。
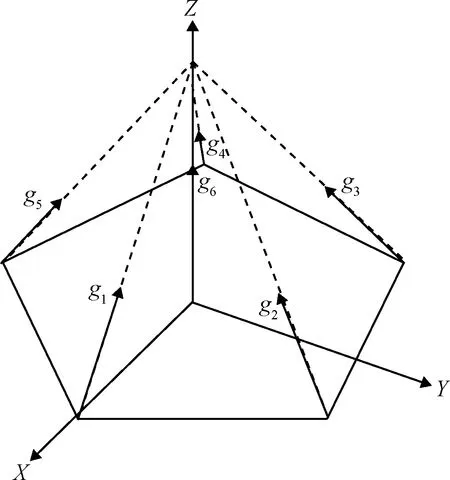
图1 五棱锥构型SGCMGs示意图Fig.1 Illustration of SGCMGs with pentagonal configuration
SGCMGs构型和框架角组合共同决定SGCMGs控制力矩的大小和方向,但在某些特定的框架角组合中,SGCMGs产生的力矩处于同一个平面内,无法提供期望的控制力矩,这种现象叫做SGCMGs奇异,也被称为内部奇异。
在ZPM中SGCMGs需要远离奇异状态。衡量SGCMGs奇异程度的参数为奇异度量m:
(8)
当奇异度量m等于0时,SGCMGs陷入奇异状态,SGCMGs的奇异约束为:
m>0
(9)
本文SGCMGs饱和是指SGCMGs的总角动量达到角动量包络面,无法继续沿角动量包络面的法线方向提供力矩,也称为外部奇异。五棱锥构型SGCMGs的包络面是有着六对凹陷的近似的球体。为了避免SGCMGs饱和,当前的研究主要是以角动量包络面上的最小振幅Hm为半径的球体作为SGCMGs框架角的可行解空间[20],设置饱和约束为:
(10)
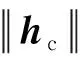
根据式(9)判断饱和约束不仅会减少SGCMGs角动量的可行域,同时仅根据SGCMGs角动量而不是框架角组合来进行规划,有时无法得到准确的SGCMGs框架角运动路径。
因此,本文基于SGCMGs框架角组合设计饱和度量b,用以衡量SGCMGs饱和状态:
(11)
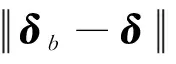
SGCMGs远离饱和状态,需要保证饱和度量b大于0,即SGCMGs的饱和约束为:
b>0
(12)
1.3 姿态约束
除了上述SGCMGs约束,航天器在ZPM过程中也面临较为复杂的姿态约束,包括姿态指向约束、有界约束和初始终端约束等[14]。
姿态指向约束缩小了ZPM中航天器的可行姿态空间。航天器必须避免强光天体进入光学元件的视场[15],姿态指向约束表示形式为:
(13)
式中:rb表示光学元件在本体系的方向;CbI表示航天器的姿态转换矩阵;ri表示强光天体在惯性系中的方向;θ是光学元件视场角。图2所示为姿态指向约束示意图。
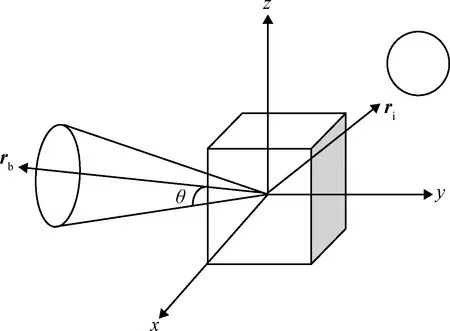
图2 姿态指向约束示意图Fig.2 Illustration of attitude pointing constraint

(14)
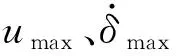
初始终端约束是指ZPM中航天器从初始平衡状态机动到目标平衡状态:
(15)
式中:q0为初始姿态;qf为目标姿态;δ0为初始框架角;δf为目标框架角;t0为初始时间;tf为终端时间。
1.4 ZPM规划模型
基于上述动力学和约束分析,建立ZPM规划模型如下:
(16)
基于ZPM规划模型对航天器姿态机动进行规划,即可得到航天器的姿态路径和SGCMGs框架角路径。
2 约束评价启发式DE算法
本文提出基于约束评价启发式的DE算法,在姿态规划空间中设计约束评价函数和启发式策略,并基于DE算法框架进行ZPM规划。
2.1 ZPM规划序列
本文在姿态规划空间中进行ZPM规划,本节设计对应的ZPM规划序列,便于后续规划。
从式(16)可以看出,ZPM问题中的航天器运动以及SGCMGs框架角运动分别位于姿态规划空间和SGCMGs框架角规划空间,且存在映射关系。3维的姿态规划空间映射到6维的框架角规划空间,单个姿态规划解对应一个或多个框架角组合规划解。
基于ZPM的规划复杂度和约束复杂性,选择在姿态规划空间中进行ZPM规划。耦合约束限制了ZPM的可行解空间和规划速度,选择姿态规划空间既可以参数化多个ZPM指标,又可以通过降维来提高ZPM规划效率。
考虑到伪谱法中节点间约束难以满足,本文在姿态空间中设计基于多段欧拉参数的ZPM规划序列P:
P=(s1,t1,…,si,ti,…,sn,tn),(i∈1,…,n)
(17)
式中:s为节点姿态参数,且si=(qi0,qi1,qi2,qi3),t为规划步长,且都为正整数,下标i表示节点序号。
在ZPM规划序列P中,以欧拉姿态机动执行规划动作,连接节点之间的姿态路径:
(18)
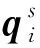
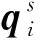
(19)
进一步地,路径旋转四元数qr为:
(20)
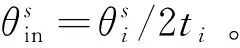
节点si和si+1之间路径集合qsi(j), (j=1,…,ti):
qsi(j)=qsi(j-1)⊗qr, (j=1,…,ti)
(21)
将式(21)带入式(17)的规划序列P中,即可得到n-1段连续姿态机动路径。在ZPM规划模型的基础上,以机动时间为目标函数,将ZPM规划问题转化为时间优化问题,在姿态规划空间中求解,得到航天器姿态路径q(t)、角速度ω(t)和SGCMGs框架角δ(t)。
2.2 约束评价启发式
ZPM问题中SGCMGs约束和姿态约束耦合,增加了规划求解难度。当前ZPM研究多是基于伪谱法进行规划[16-18],但是伪谱法在约束增多的情况就会出现规划效率降低和难以满足节点间约束的情况。且多数研究仅考虑SGCMGs约束,忽略了姿态指向等姿态约束。
面对多种ZPM约束耦合难以处理的问题,本文设计约束评价启发式,以期快速引导ZPM规划序列满足上述约束。
首先,基于ZPM过程中约束的影响机理对ZPM约束进行解耦分类处理。航天器姿态指向约束和有界约束分别在三维空间指向和节点间距离方面对ZPM路径进行限制,SGCMGs奇异和饱和约束同时在SGCMGs框架角组合方面进行限制。因此根据其约束机理设置姿态指向约束评价函数、有界约束评价函数、SGCMGs奇异和饱和约束评价函数。
然后,针对约束评价函数,设计启发式策略,引导ZPM规划序列P满足上述多种约束。约束评价启发式以约束处理为主要关注目标,具体过程如下。

(22)
式中:k代表姿态指向约束区域序号;θk为对应的约束区域视场角。
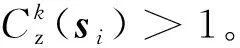
(23)
式中:
(24)
式中:I3表示3阶单位矩阵。
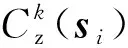
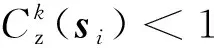
(25)
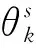
(26)
通过候选安全节点sp替换约束节点si,启发式引导规划序列P满足姿态指向约束:
(si,ti)=(sp,tp)
(27)
在有界约束启发式方面,不涉及路径指向,主要考虑路径中的节点距离。有界约束和规划步长ti负相关,通过限制路径的控制力矩和角速度压缩节点间空间距离。值得注意的是,这里的规划步长ti指的是姿态规划序列P中节点间的机动时长。
因此,这里将有界约束满足问题转化为规划步长ti选择问题。通过节点空间距离和有界约束上限来估计规划步长ti,设计有界约束评价函数Cd(si)来判断约束区间和约束程度,采用评估Cd(si)引导规划序列满足有界约束的启发式策略。
Cd(si)=Cd(uc)+Cd(ω)
(28)
在姿态规划空间中,控制力矩和角速度同时影响规划步长ti,因此有界约束评价函数Cd(si)由控制力矩和角速度对规划步长ti的评价函数Cd(uc)和Cd(ω)组成:
(29)
式中:uc(k)和ω(k)表示从节点si和节点si+1的中间路径的控制力矩和角速度,规划步长ti对应中间路径的机动时长,w1和w2分别表示控制力矩和角速度的估计权值,满足w1+w2=N1:
(30)
式中:N1为权值系数;w1和w2互斥是因为在同一节点处只有一种有界约束处于主导位置。
当Cd(si)>1时,节点si违反有界约束。通过Cd(si)判断P中违反有界约束的节点、违反程度以及对应的约束项,同时用于生成新的规划步长。基于当前规划步长ti和对应的Cd(si)估计满足有界约束的规划步长td:
td=ceil(tiln(Cd(si))+1)
(31)
其中,ceil( )表示返回大于或者等于指定表达式的最小整数。
通过候选安全节点td替换约束节点规划步长ti,引导规划序列P满足姿态指向约束。
在SGCMGs奇异和饱和约束启发式方面,ZPM规划序列P在姿态空间进行规划,此时无法直接对SGCMGs奇异和饱和约束判断。因此设计SGCMGs奇异和饱和躲避规划操纵率,采用SGCMGs奇异约束评价函数Cm(si)和饱和约束评价函数Cb(si)来判断约束区域和约束违反程度,再通过评估Cm(si)和Cb(si)引导规划序列满足约束的启发式策略:
(32)
式中:δi表示si对应的SGCMGs框架角组合。当Cm(si)和Cb(si)都大于0时,SGCMGs满足奇异和饱和约束。
通过对五棱锥构型的内部奇异点和外部奇异点分析,设计基于势函数思想[10]的SGCMGs奇异和饱和躲避规划操纵率,用于SGCMGs框架角运动提供航天器要求的指令力矩。
在框架角规划空间中,设计SGCMGs内部奇异点持续排斥δi,SGCMGs外部奇异点先吸引再排斥的SGCMGs框架角运动规律,得到对应的框架角转动矢量di的吸引势函数Vai和排斥势函数Vpi:
(33)
式中:w3和w4分别表示对应的势函数权值。通过式(33)得到框架角转动矢量di:
2w4(Cb(si))2
(34)
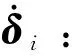
(35)

2.3 启发式DE规划
ZPM约束评价启发式能够处理ZPM过程中的复杂约束,可以和多种优化方法结合进行启发式规划,这里和DE算法结合进行启发式DE规划。
DE算法通过适应度函数对种群进行评价,通过变异交叉得到中间种群,基于适应度函数判断是否得到最优个体[21]。启发式DE规划方法用启发式约束评价函数更新适应度函数,将约束评价启发式放入DE算法的变异过程中,快速引导规划序列满足多种约束。下面是约束评价启发式的DE应用以及算法改进部分。
机动时间作为优化适应度函数:
Jt=tf
(36)
在启发式变异方面,考虑到ZPM问题约束的复杂性,在变异进程中优先进行约束处理,通过判断评价函数是否超出评价阈值Cw,进行如式(37)的约束评价启发式规划。当满足约束之后,则进行变异操作,优化总适应度函数Jz。启发式变异向量vj,G+1如下产生:
vj,G+1=
(37)
而突变算子F的取值影响算法的搜索空间和效率,F越大搜索范围越广,这里将F设置为根据规划进程可变的形式:
F=exp(-fi/fmax)w
(38)
式中:fi是当前节点数;fmax是总节点数;w是控制参数。这样突变算子F在规划前期较大后期较小,这样具有较好的前期全局规划能力以及后期收敛速度。
根据总适应度函数Jz将最优个体与当前种群中的个体向量进行比较,选择是否保留当前个体,逐代更新,得到ZPM的最优解。
3 仿真校验
本节进行了多种约束条件下航天器ZPM规划仿真,以校验本文提出的启发式DE规划算法的有效性。
在仿真验证中,航天器仅由SGCMGs提供控制力矩进行姿态机动,构型为五棱锥构型,每个SGCMG的转子角动量为1000 N·m·s。航天器在z轴方向安装光学相机,方向矢量由rb表示,其需要躲避的明亮天体的指向分别是ri1、ri2、ri3和ri4,视场角θ1、θ2和θ3是30°,θ4是25°,其他仿真参数见表1。

表1 仿真条件Table 1 Simulation conditions
通过启发式DE方法,对ZPM进行仿真验证,仿真结果如下。
图3到图5分别给出ZPM过程中的姿态参数、控制力矩和角速度。图3显示航天器能够实现从初始姿态q0到目标姿态qf的平稳机动,满足初始终端约束。图4和图5显示由SGCMGs提供的控制力矩以及航天器角速度都没有超出上限值,满足有界约束。本文的离散ZPM规划序列节点,节点之间的路径通过欧拉姿态机动连接,因此控制力矩主要施加在节点处,保证节点间的机动连续性和角速度的平稳性。
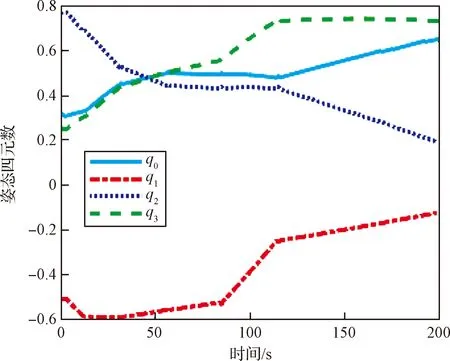
图3 ZPM姿态四元数曲线Fig.3 ZPM attitude maneuver quaternion curve
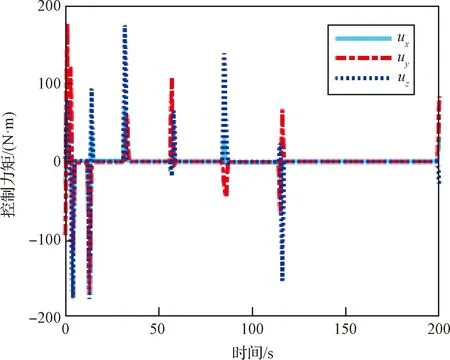
图4 ZPM控制力矩曲线Fig.4 ZPM control torque curve
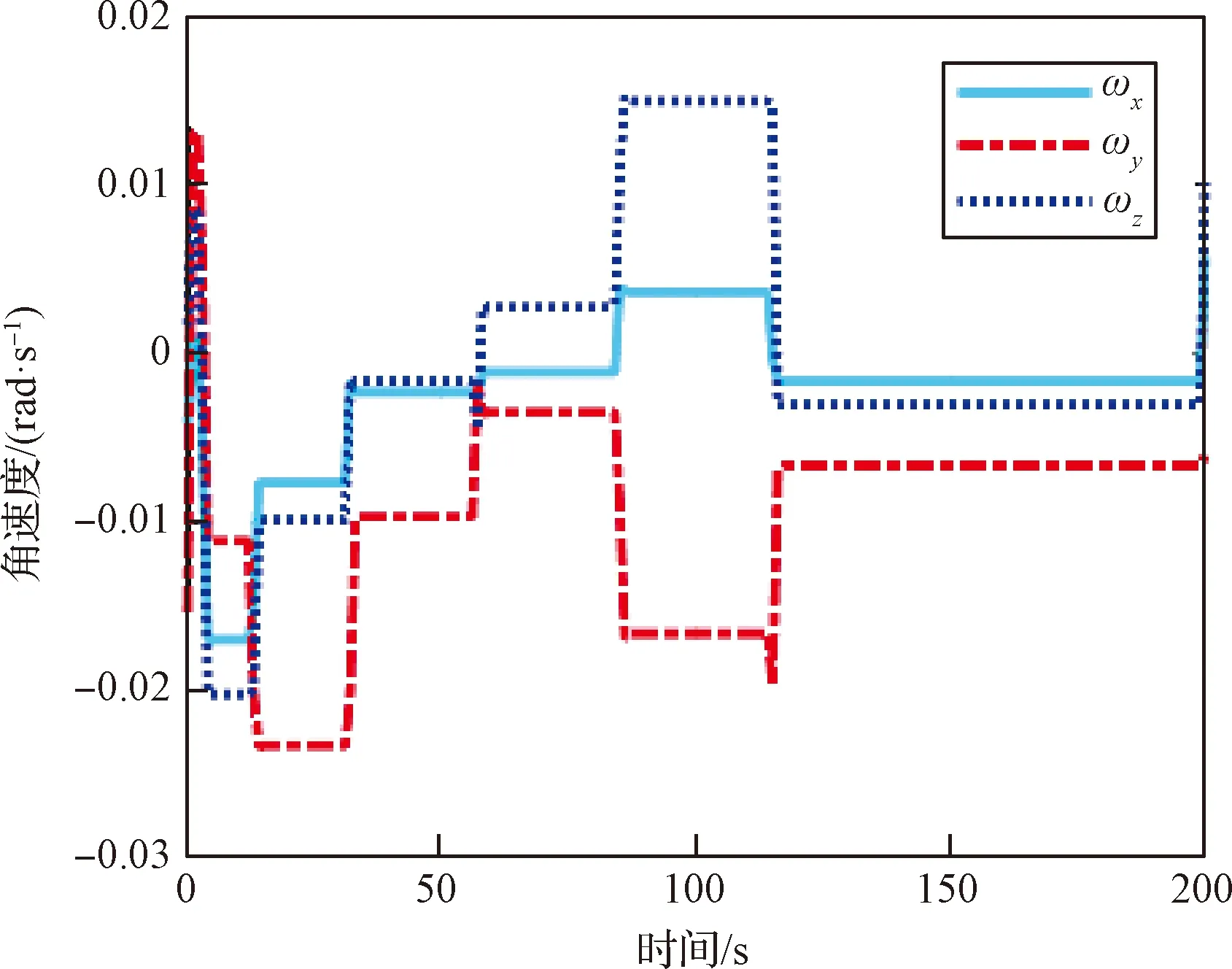
图5 ZPM角速度曲线Fig.5 ZPM attitude angular velocity curve

图6 SGCMGs奇异度量Fig.6 Singular measures of SGCMGs

图7 SGCMGs饱和度量Fig.7 Saturation measurement of SGCMGs
图6和图7给出ZPM过程中SGCMGs的奇异度量和饱和度量。图6显示机动过程中SGCMGs一直远离奇异状态,满足奇异约束,图7显示机动过程中SGCMGs能够避免进入饱和状态,进而实现了航天器通过SGCMGs实现ZPM机动,无需消耗燃料。
图8和图9分别给出ZPM过程中航天器在天球坐标下的投影路径和空间路径。图8中的椭圆和图9中的圆形区域表示姿态禁止机动区域,实线为航天器姿态机动路径。为了验证本文约束评价启发式的约束处理能力,将禁止区域密集设置。可以看出,在ZPM过程中光学相机能够安全通过密集的禁止机动区域,有效满足姿态指向约束,得到安全的ZPM路径。
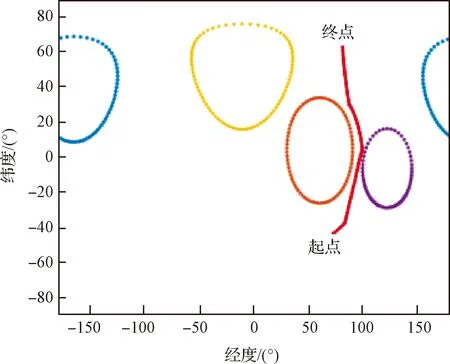
图8 天球坐标系投影下航天器姿态路径Fig.8 Spacecraft attitude path estimation based on celestial coordinate projection
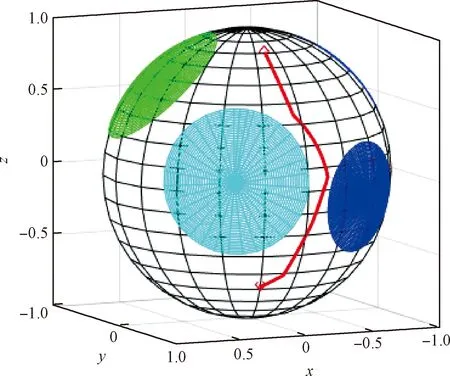
图9 天球坐标下航天器空间三维姿态路径Fig.9 Three-dimensional attitude path of spacecraft in celestial coordinates
为了验证本文提出的启发式DE方法的有效性,将启发式DE方法和ZPM伪谱法[16]进行对比。仿真条件和约束设置相同,计算机主频为3.2 GHz,内存是4 G,同时考虑SGCMGs约束和姿态约束,规划结果对比见表2。
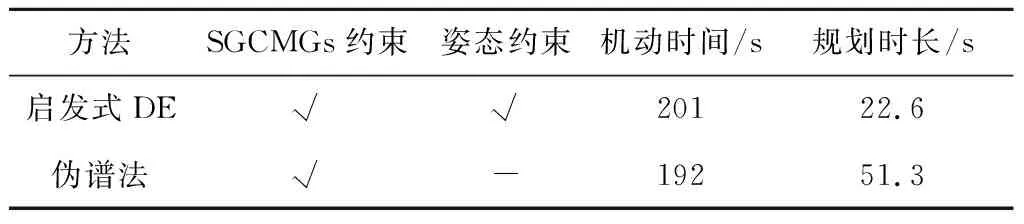
表2 规划方法对比Table 2 Comparison of planning methods
由表2可知,本文的启发式DE方法和伪谱法[16]都能够有效地处理SGCMGs约束。但是在考虑密集姿态约束的情况下,伪谱法难以得到满足姿态约束的ZPM路径。而本文的启发式DE方法可以同时满足SGCMGs约束和姿态约束,得到安全的ZPM路径。
值得注意的是,本文提出的启发式DE方法的规划时长与伪谱法相比减少了约56%,说明启发式DE方法有更高的规划效率,能够实现快速ZPM规划。而且,启发式DE方法和伪谱法的路径机动时间相差不大,说明启发式DE方法同样也具有较好的时间优化效果。
综上看出,通过本文提出的启发式DE方法,航天器能够在姿态机动中通过SGCMGs实现零推进剂消耗。该方法通过约束评价启发式引导,保证航天器满足SGCMGs约束和姿态约束。平滑的姿态曲线表明该方法可以生成质量较好的平稳机动路径,控制力矩和角速度低于上限值说明满足姿态有界约束,姿态路径曲线没有经过阴影区域说明满足姿态指向约束,SGCMGs奇异度量和饱和度量全程都大于0说明SGCMGs远离奇异和饱和状态。同时该方法和伪谱法[16]相比缩短了规划时长,具有更好的约束处理能力和规划速度。而且通过欧拉机动连接路径节点,能够保证ZPM路径连续平稳,适合进行航天器ZPM应用。
4 结 论
本文研究了多种约束情况下的航天器ZPM问题,通过对SGCMGs和航天器进行约束和复杂度分析,针对耦合约束设计约束评价启发式,结合DE算法进行启发式DE规划,并采用欧拉机动保证路径的连续性。通过仿真验证了该方法在解决ZPM问题方面的有效性和快速性,可以生成平滑的姿态四元数曲线,保证航天器满足姿态约束,通过约束评价启发式引导奇异和饱和度量避免SGCMGs陷入奇异和饱和状态,和伪谱法相比具有较好的约束处理能力和规划速度。该方法能够实现姿态机动的零推进剂消耗,得到安全的ZPM路径,在航天器姿态机动领域有较好的应用前景。

