气体辐射与流场耦合对火星进入热环境影响
聂春生,聂 亮,杨 光,袁 野
(中国运载火箭技术研究院空间物理重点试验室,北京 100076)
0 引 言
火星大气环境十分稀薄,主要由95.7%的CO2、2.7%的N2和少量的Ar及其他组分组成[1];其中,CO2气体具有多个振动模态,热化学特性复杂,对火星高速进入过程中的高温流场和热环境数值模拟提出了新的挑战。国外针对火星高温流场数值模拟开展了大量研究,McKenzie[2],Park等[3]先后给出了不同的适用于火星高速进入问题的非平衡化学反应模型;Chen等[4]研究了化学模型、表面催化、输运参数等对火星探测器热表面热流的影响。Milos等[5]研究了探路者号进入器动加热与防热材料的相互作用。美国火星科学试验室的飞行重建数据表明火星再入过程中存在比地球环境更为显著的气体辐射加热[6]。Fujita等[7]的研究结果表明火星进入飞行器后部辐射加热和对流加热是可比拟的,并且前部的辐射加热要比后部强。Rond等[8]在激波管实验中研究了激波后的CO2-N2-Ar混合气体的非平衡辐射,试验测量了激波后的辐射通量,并与采用多温度的动力学模型和辐射代码计算的辐射热流进行比较,并对化学速率常数进行了修正。Johntson等[9]的研究结果表明火星大气的辐射机理较为复杂,波长范围很广,高温气体辐射加热是火星进入热防护设计中不确定性的主要来源之一。国内火星探测研究起步相对较晚,针对火星进入器的热环境研究公开文献较少,但也有一些学者开展过相关研究。杨肖峰等[10-11]针对火星和地球大气分子热力学和化学行为的差异性,研究探测器高速进入过程中流场的真实气体效应,获得不同气体模型条件下的气动加热规律。刘庆宗等[12-13]针对典型火星探测器,数值研究了不同表面催化特性和表面温度条件对气动力热的影响。苗文博等[14]采用数值模拟方法研究不同热力学模型中火星飞行器表面的热环境。吕俊明等[15]在简述火星探测和气体辐射研究发展历程的基础上,综述了火星进入气体辐射加热研究进展,展望了未来火星进入气体辐射加热研究方向,提出了研究建议。陈彪[16]采用非耦合方法计算了MSL火星探测器飞行流场中CO2及CO对防热大底的辐射热流。
总的来看,国内研究较多的是高温流场的热化学非平衡效应、表面催化特性等对火星再入飞行器气动力、热的影响,对气体辐射加热的研究较少;国外部分学者针对火星大气辐射加热问题开展了相关研究,关注的重点是CO2气体的辐射特性参数问题,针对火星进入器辐射加热计算主要采用非耦合方法,不考虑高温流场非平衡效应与气体辐射之间的影响,预测结果相对保守。随着火星探测任务需求的不断提高,未来的火星进入器将具有更大尺寸和更快的进入速度,必然会面临严重的气体辐射加热问题,先进防隔热系统设计需要考虑高温气体辐射与非平衡流场的耦合效应,对辐射加热进行精细考虑。本文通过求解含有辐射源项的热化学非平衡N-S方程,发展了兼顾计算精度和效率的流动辐射耦合计算方法,考虑流场和辐射场之间的耦合干扰效应,分析了探路者进入火星大气时气体辐射与流动耦合作用对飞行器气动加热特性的影响规律,研究了飞行器进入过程中不同高度的流场非平衡特性以及不同表面催化特性对对流加热和辐射加热的影响。
1 计算方法
1.1 数值计算方法
对于高温火星大气非平衡气体流场,求解积分形式的含化学反应的多组元N-S方程[17],守恒形式的控制方程如下:
(1)
式中:Q为守恒量;F、G、H与FV、GV、HV为分别表示不同方向的对流项与黏性项;W为非平衡源项。
其中,对两温度模型(2T):
Q=[ρi,ρu,ρv,ρw,ρe,ρeve]T,
W=[wi,0,0,0,Qrad,Qve]T
其中,对一温度模型(1T):
Q=[ρi,ρu,ρv,ρw,ρe]T,
W=[wi,0,0,0,Qrad]T
式中:ρi是组分i的密度;u、v、w为直角坐标系下的速度;e为总能;ev为分子组分的总振动能;wi是组分i的化学非平衡源项;Qrad是辐射能量源项;Qve是振动非平衡源项。
采用有限体积法求解控制方程,无黏通量离散求解采用Roe平均方法与Yee的对称TVD限制器,并对特征值采用了Harten的熵修正[18];黏性通量离散求解采用了中心差分格式;时间推进采用了全隐式LU-SGS方法,非平衡源项采用隐式处理[19]。
1.2 物理化学模型
气体化学反应模型采用包含CO2-N2混合气体的化学反应体系,考虑CO2多振动能级的热力学一温度和两温度模型。
本文计算的化学反应模型见表1,考虑了CO2、CO、N2、O2、NO、C、N、O、CN、C2、C+、O+、NO+、O2+、CO+、e-共计16个组分,化学反应速率常数参考文献[3]。
在热力学一温度模型中,假设表征平动、转动、分子振动激发以及电子激发的温度是相等的,只用一个温度T来描述。
在热力学两温度模型中,假设分子振动能与平转动能不平衡,分别用平转动温度Ttr和振动温度Tve来描述。对于两温度模型,用来反映式(1)中振动-电子能交换的源项:
(2)
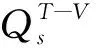
(3)
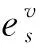
表面材料的催化特性一般按完全非催化条件(NCW)和完全催化条件(FCW)两种方法处理。

表1 火星大气高温化学反应模型Table 1 Chemical reaction model
1.3 辐射特性与传输模型
考虑沿辐射方向的气体介质的定常辐射输运方程的一般形式可以写为[17]:
(4)
式中:Iσ(u)为u方向、波数σ的辐射强度;η为辐射系数;κ为吸收系数;s为与计算点的距离。
气体辐射与非平衡流场的耦合作用以能量方程的源项形式体现在流体控制式(1)中,发射对应控制体能量的减少,吸收对应控制体能量的增加。对于编号为i的有限控制体,辐射源项为:
(5)
飞行器表面的辐射热流计算公式如下:
(6)
辐射特性参数计算主要考虑如下高温气体辐射机制:
1)CO的第四正带系(A1∏-X1∑+,波长120~280 nm)
2)CO的第三正带系(b3∑+-a3∏r,波长250~450 nm)
3)CO的Triplet带系(d3Δi-a3∏r,波长320~2500 nm)
4)CO的Asundi带系(a′3∑+-a3∏r,波长370~2500 nm)
5)CO的Angstrom带系(B1∑+-A1∏,波长400~700 nm)
6)CO的红外带系(X1∑+-X1∑+,波长1200~7000 nm)
7) CN的Red带系(A2∏i-X2∑+,波长400~2800 nm)
8)CN的Violet带系(B2∑+-X2∑+,波长300~550 nm)

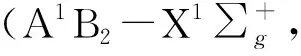
为了减小耦合辐射源项的流场控制方程计算量,本文采用了切平板近似法进行辐射输运方程的求解;辐射特性参数计算采用Chamber提出的改进转动平滑谱带SRB模型[21-22],该方法将转动光谱结构进行平滑并用指数模型进行描述,通过SRB模型生成分子辐射物性参数数据库所需的参数和存储空间要远远小于逐线计算,适用于为气体辐射和非平衡流场耦合计算;计算过程中采用的光谱数据均来自参考文献[23-24]。
长期以来,中国传统的家庭教育一直缺乏科学理论的指导。有些家庭受传统思想的影响,成天抱着“望子成龙”的心态,把孩子视为自己的私有财产,将其看成一个雏形的成人,把自己没有实现的愿望强加在孩子身上,缩短了其幼儿时期。家庭教育也存在很大的盲目性,如盲目投资、盲目施教、盲目要求、盲目攀比等,这些都给幼儿的心理带来过重的压力。
2 算例验证
为验证计算方法的正确性,选取了MESUR大底外形算例[4],计算状态见表2,化学反应采用Park的18组元反应模型,热力学模型采用双温模型,壁温设置为辐射平衡壁温,壁面发射率取0.9,完全非催化壁条件。
图1给出了表面热流计算结果与国外参考文献[4]的对比,可以看到热流偏差均在5%以内,计算方法的正确性得到验证。
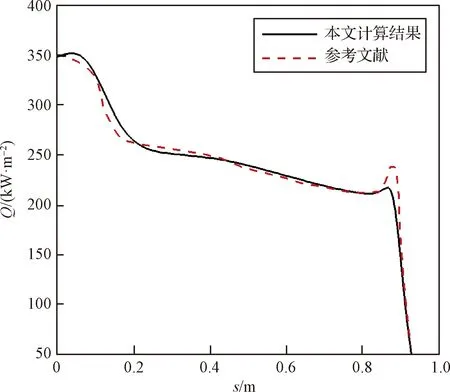
图1 表面热流Fig.1 Surface heat flux
3 计算模型
选取探路者号火星探测器开展气体辐射与非平衡流场耦合对热环境的影响分析。探测器的防热大底为头部半径为0.6625 m的70°球锥外形,整体外径为2.65 m,肩部半径为0.06625 m,具体尺寸如图2(左)所示[25]。
探路者号火星探测器釆用零攻角弹道式进入火星大气层,可简化为二维轴对称问题。这里选用对气动和防热影响最为严重的前体防热大底作为研究对象。计算网格见图2(右),其中边界层内和激波线附近的网格进行加密,壁面法向网格雷诺数Re=5,壁面温度取300 K;计算来流条件选取探路者飞行轨迹的典型状态,参数见表3。

表2 MESUR探测器计算状态Table 2 Computational condition of MESUR probe
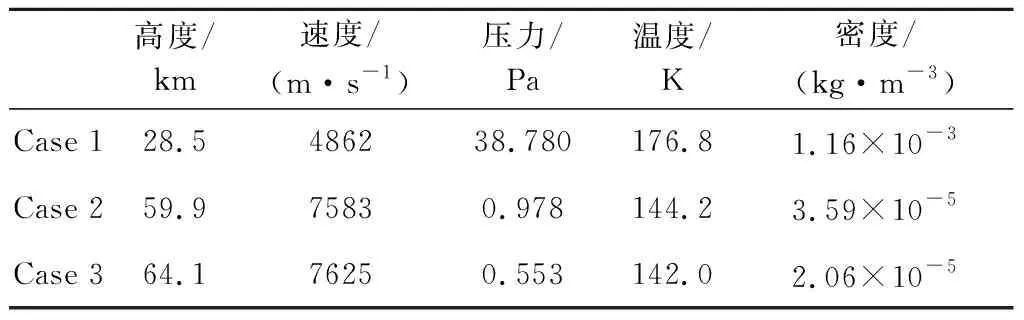
表3 来流条件参数Table 3 Freestream conditions
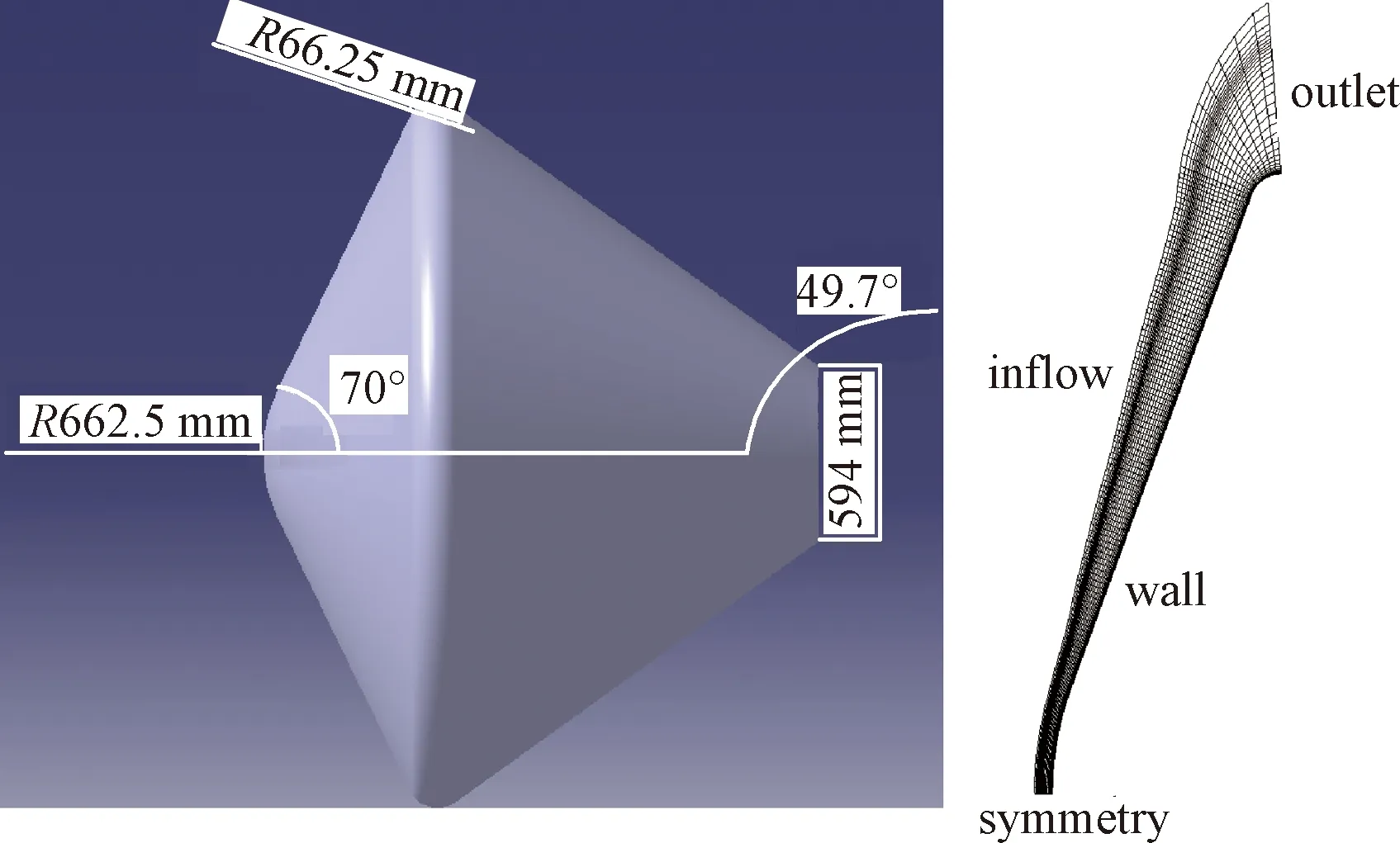
图2 探路者号火星探测器几何尺寸及计算网格Fig.2 Schematic of the tangent slab approximation and grid
4 计算结果分析
4.1 非平衡流场和气动加热分析
图3给出了探测器在高度28.5 km的流场密度、压力、平动温度及振动温度云图,可以看出,高速气流在探测器防热大底之前产生一道很强的脱体弓形激波,形成较薄的激波层,波后气体被强烈压缩,形成了很强的高温高压环境,气体的振动温度激发并发生复杂的化学反应,高温化学反应混合气体随流动向下游发展,将探测器大底包裹在强烈的热化学非平衡反应气流中。
图4给出了高度28.5 km状态沿驻点线的流场参数曲线,其中热力学模型采用了一温度(1T)和两温度模型(2T),可以看出探测器大底前的流场在激波后的温度和压力很高,两温度模型的温度计算结果与单温度模型有一定差异,激波层内振动温度略低于平动转动温度,并存在温度的弛豫现象;沿驻点线,激波层内气体最高温度可达到7000 K以上,CO2气体发生大规模离解反应,离解程度超过了80%,化学反应非常剧烈,主要生成产物为CO,质量分数约0.4,其它气体组分浓度较低;对于流场压力,不同温度模型计算结果接近,波后压力约26 kPa,温度模型对压力计算影响相对较小。
图5给出了高度59.9 km状态沿驻点线流场参数曲线,可以看出在更高高度以更高速度飞行时,会形成更强的脱体激波,但由于高空来流更加稀薄,使得波后被压缩的气体峰值压力下降明显,波后压力约2 kPa,但激波层内的峰值温度显著加,激波附近的最高平动转动温度可达到33000 K以上,振动温度超过了10000 K,激波脱体距离增大,激波层增厚;高温气体的离解组分的分布规律与Case1状态大体类似,但由于激波层内温度更高,因此CO2的离解程度更高,超过了98%;CO组分的生成量也进一步增加,质量分数超过了0.5;气体中的N2和CO组分也发生离解反应和电离反应,产生了大量的C+、O+、CO+等带电粒子,热化学反应更加剧烈,流场的非平衡程度显著增大。
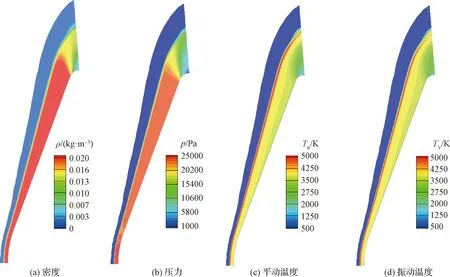
图3 探路者号火星探测器流场(Case 1)Fig.3 Flow field of Pathfinder Mars probe(Case 1)

图4 沿驻点线流场参数曲线(Case 1: 28.5 km)Fig.4 Parameter curve of flow field along stagnation point line (Case 1: 28.5 km)
Case 1和Case 2对比可以看出,飞行器火星进入过程中,在高空以较高速度飞行,流场中的气体密度相对较低,流动具有明显的热力学非平衡特征,随着飞行高度降低速度减小,流动逐渐向趋于热力学平衡状态发展,但在火星环境下,28.5 km高度的流场仍呈现出一定的热化学非平衡特征。
图6、图7给出了不同温度模型和不同表面催化特性的表面压力和热流对比曲线,可以看出不同催化条件下表面压力量值基本相同,但热流存在明显差异,其中Case 2工况最大差异超过了50%。其次,不同热力学模型对热流也会产生一定差异,这种差异受壁面催化条件影响,当壁面为完全催化壁时,不同热力学模型所得热流基本一致,最大相差不超过5%;当壁面为完全非催化壁时,不同热力学模型之间热流差异越明显,两温度模型计算的热流高于一温度模型,头部驻点区差异最大约为20%左右;因此要进行火星进入热防护设计,从设计可靠性的角度考虑应该选择热力学非平衡模型,并选择更加准确的表面催化模型进行热环境计算。
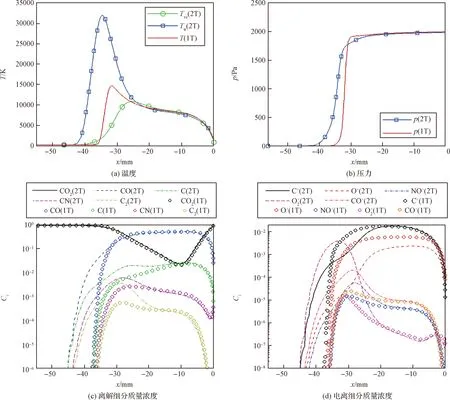
图5 沿驻点线流场参数曲线(Case 2: 59.9 km)Fig.5 Parameter curve of flow field along stagnation point line (Case 2: 59.9 km)
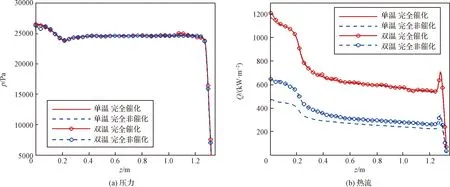
图6 表面压力和热流对比曲线(Case 1: 28.5 km)Fig.6 Comparison curve of surface pressure and heat flow (Case 1: 28.5 km)
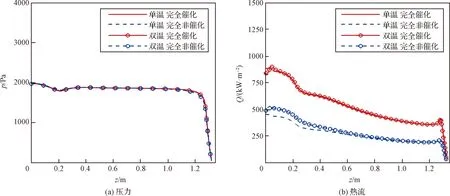
图7 表面压力和热流对比曲线(Case 2: 59.9 km)Fig.7 Comparison curve of surface pressure and heat flow (case 2: 59.9 km)
4.2 气体辐射与非平衡流场耦合影响分析
图8、图9分别给出了高度为59.9 km、64.1 km两个状态,采用气体辐射与非平衡流场耦合计算与非耦合方法计算得到的流场平动温度、振动温度的对比,其中非平衡流场计算采用两温度模型,表面采用完全催化条件;计算结果表明,高温气体辐射与非平衡流场耦合计算会使激波的脱体距离减小约5~10%,其中驻点区域由于激波的压缩性最强,使得驻点区域激波的脱体距离改变量小于远离驻点的区域的激波;而高温气体辐射与非平衡流场之间的耦合干扰效应对激波层内气体温度大小和温度松弛距离的影响较小,松弛距离仍然保持约10~20 mm长度,其中驻点线上的松弛区最短。
图10、图11分别给出了高度为59.9 km、64.1 km两个状态采用耦合和非耦合方法得到的表面热流分布,可以看出:1)由于流场中CO2气体发生大规模离解反应生成了大量的CO组分,而CO气体的真空紫外辐射会产生较强的气体辐射加热,使得壁面的辐射热流占对流热流的比例约为15~45%,靠近肩部区域比例最大;2)对于整个飞行器防热大底,对流热流在驻点最大,向肩部逐渐降低;而辐射热流随位置的变化较小;3)考虑气体辐射对流场的冷却效应,会对表面热流产生一定影响,其中对流热流变化较小,而辐射热流变化较大,耦合方法计算得到的辐射热流相比非耦合方法会减小约12~25%,其中驻点区域的减小量相对较小,这主要是因为高温气体辐射与非平衡流场之间的耦合干扰效应对驻点区域的激波脱体距离影响相对较小,激波层内的产生高温气体辐射的气体与壁面的距离变化小导致的。
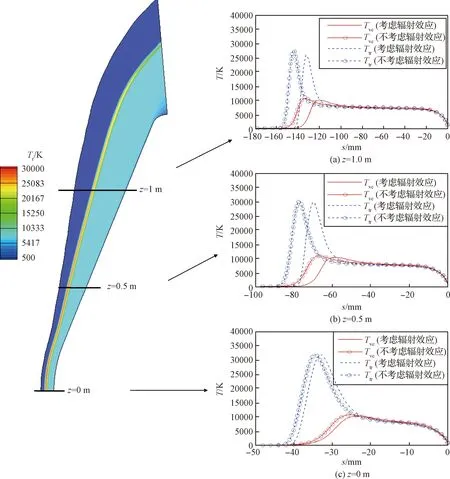
图8 耦合与不耦合气体辐射效应对温度的影响(Case 2: 59.9 km)Fig.8 Effects of coupled and uncoupled gas radiation on temperature profile (Case 2: 59.9 km)
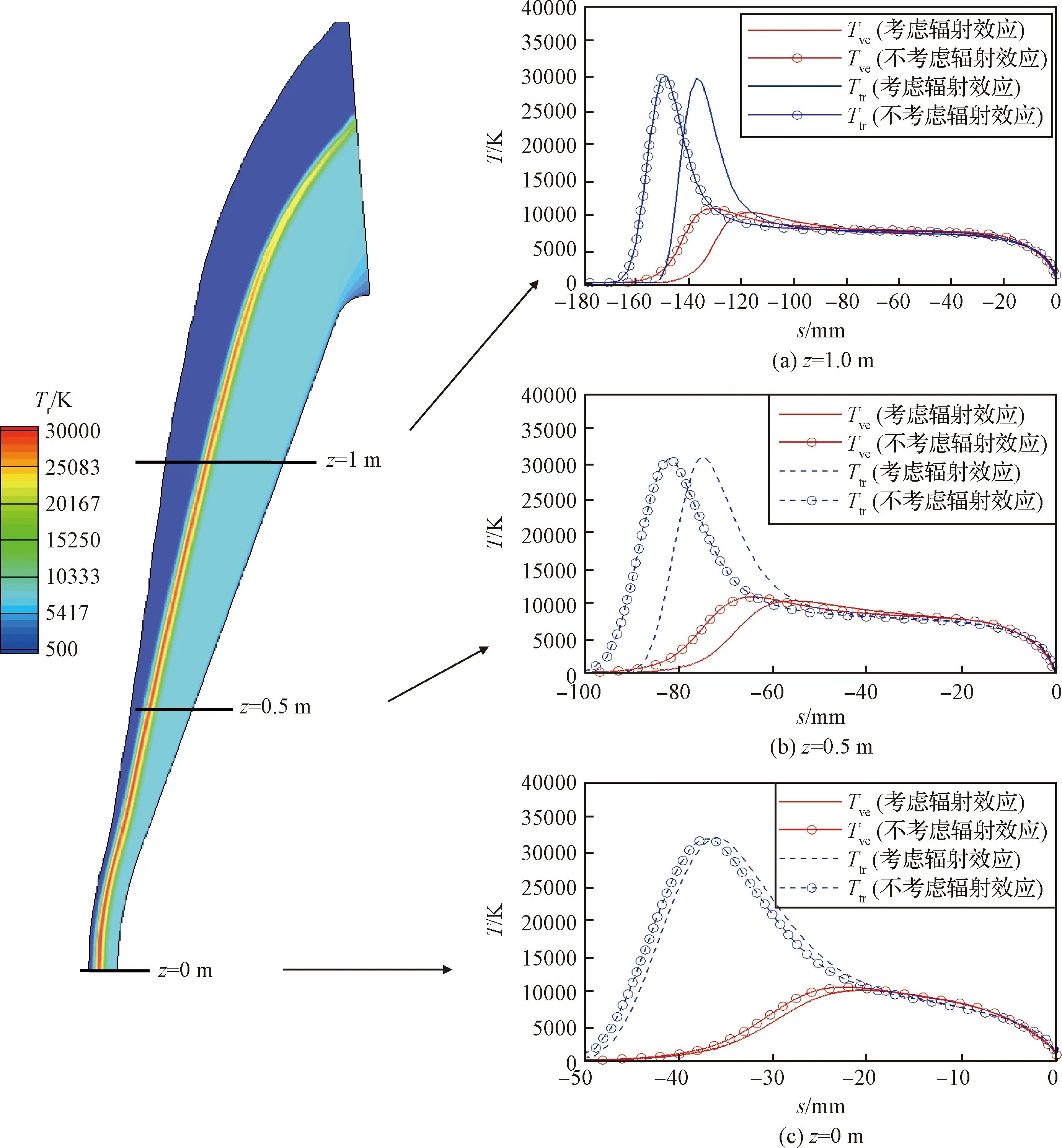
图9 耦合与不耦合气体辐射效应对温度剖面的影响(Case 3: 64.1 km)Fig.9 Effects of coupled and uncoupled gas radiation on temperature profile (Case 3: 64.1 km)
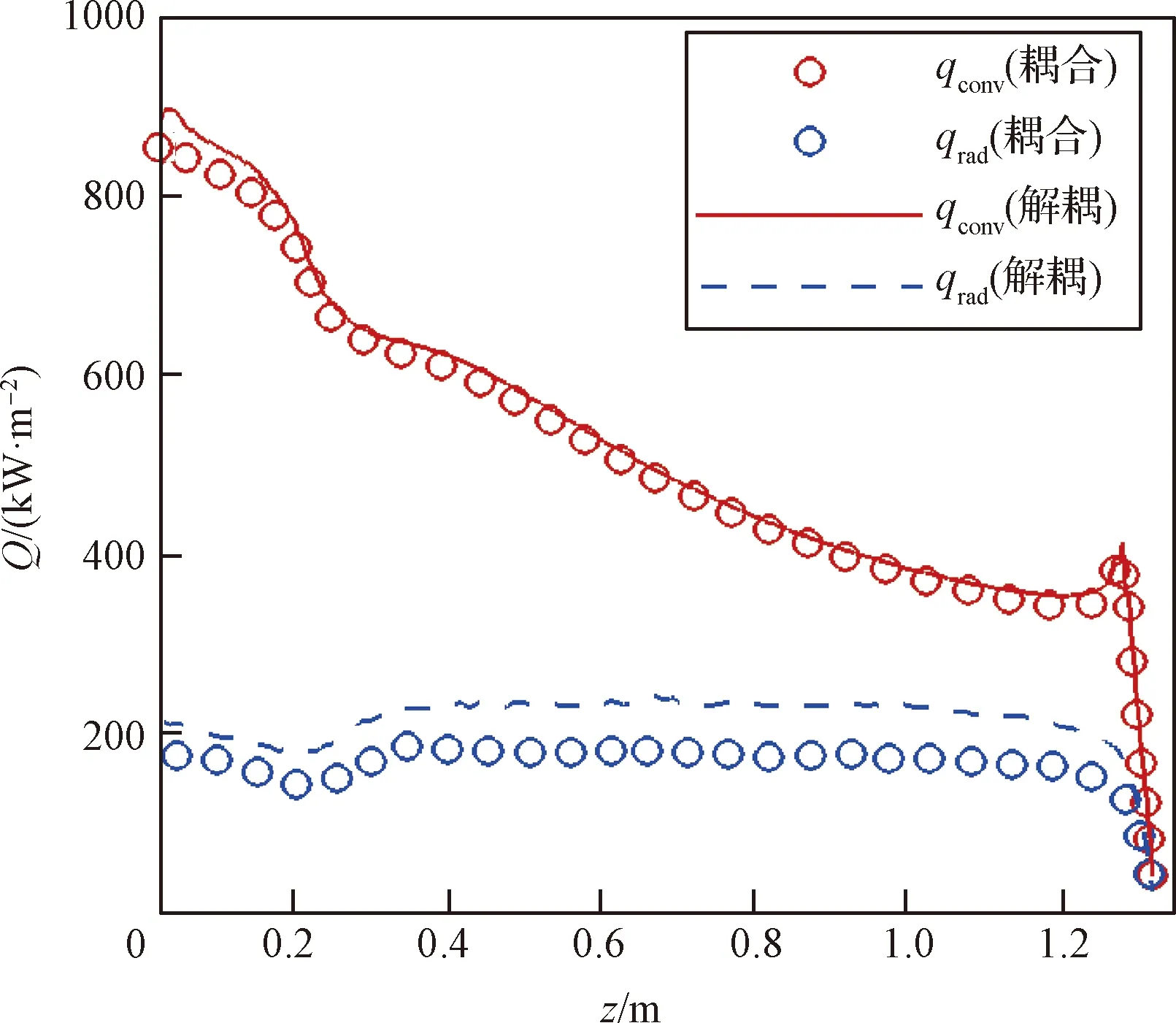
图10 气体辐射与非平衡流场耦合计算的表面热流分布(Case 2: 59.9 km)Fig.10 Surface heat flux distribution for coupled calculation of gas radiation and non-equilibrium flow field(Case 2: 59.9 km)
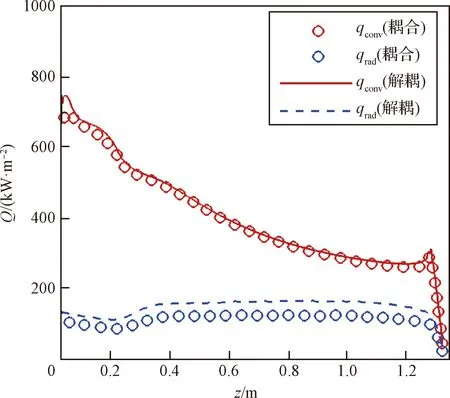
图11 气体辐射与非平衡流场耦合计算的表面热流分布(Case 3: 64.1 km)Fig.11 Surface heat flux distribution for coupled calculation of gas radiation and non-equilibrium flow field (Case 3: 64.1 km)
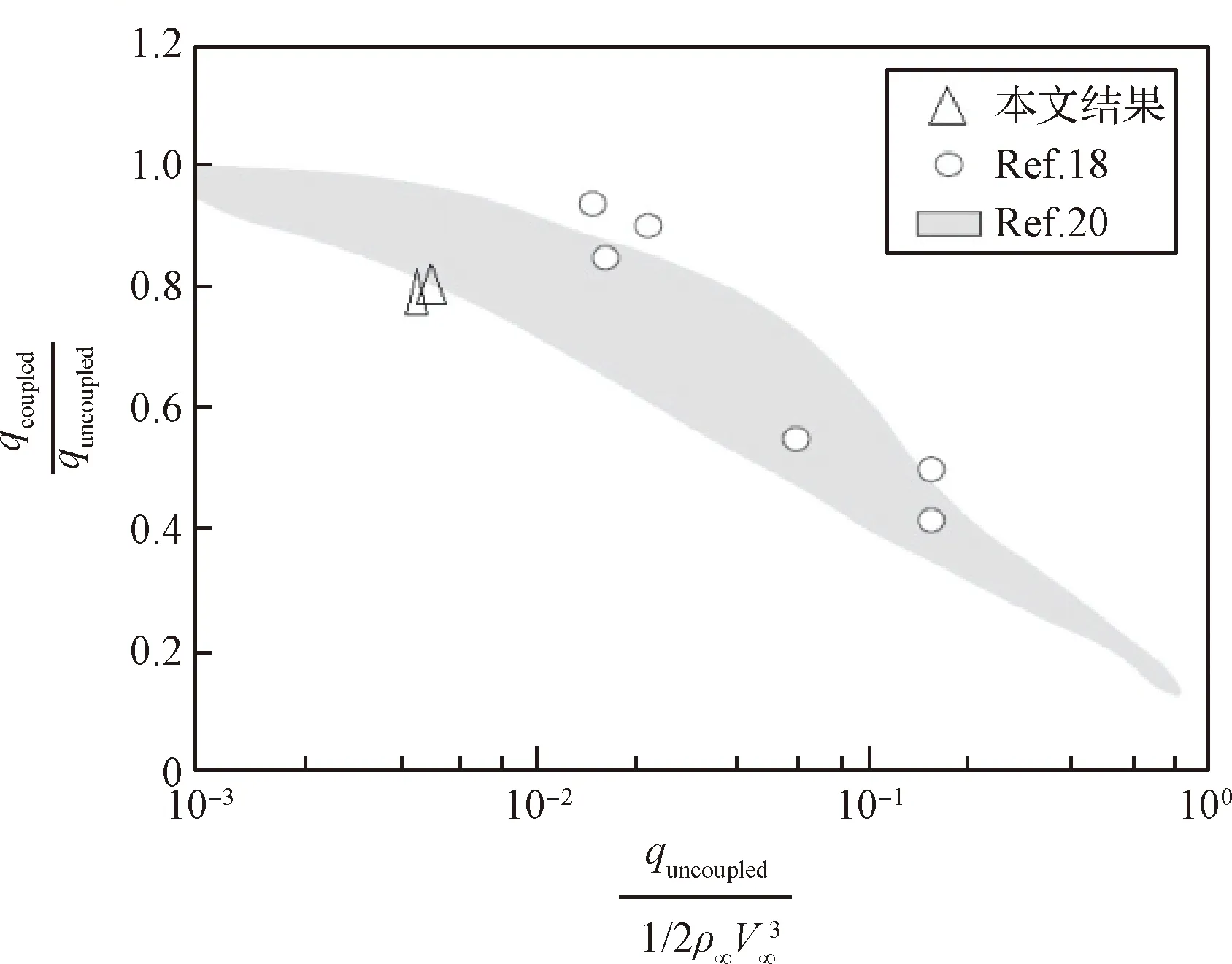
图12 气体辐射冷却因子Fig.12 Radiation cooling factor of gas
5 结 论
针对探路者号火星探测器,采用数值模拟方法,研究了高速进入火星过程中高温气体辐射效应与非平衡流场耦合作用对热环境的影响,得到以下结论:
1)进入火星的过程中防热大底前会形成很强的弓形激波,激波层内的高温高压气体的热化学非平衡效应非常严重,在28.5 km高度仍然存在一定的温度松弛现象,流场中CO2气体发生大规模离解反应生成CO;
2)热力学模型、表面催化特性对表面热流计算有着重要的影响,完全催化热流要高于完全非催化热流50%以上,热力学模型的影响与表面催化特性相关;
3)高温流场中CO气体组分会产生较强的气体辐射加热,辐射热流占对流热流的比例约为15%~45%,靠近肩部区域比例最大;
4)高温气体辐射与非平衡流场耦合计算会使激波的脱体距离减小约5%~10%,但对激波后温度的大小和松弛距离影响较小;气体辐射对非平衡流场的冷却效应会使辐射热流降低约12%~25%,但对流热流受影响很小。因此,随着气体辐射显著增强,需要耦合考虑气体辐射、非平衡流动的相互作用和影响规律,采用耦合计算方法进行表面辐射热流的精细预测。

