预测与反演交会制导的燃料消耗遗传算法寻优
谭天乐
(1.上海航天控制技术研究所,上海 201109; 2.上海市空间智能控制技术重点实验室,上海 201109)
0 引 言
受燃料补给限制,目前大部分航天器全寿命期间所具有的轨道机动能力有限。对于交会对接、悬停、绕飞等空间相对制导任务,如何实现燃料消耗最优一直是理论和工程上的热点、难点问题。
国内外空间相对轨道机动的轨迹规划方法包括间接法和直接法[1]。直接法把控制变量或状态变量离散和参数化,将最优控制问题转换为非线性规划问题;直接法易收敛,但计算量大,且容易收敛到局部最优解。间接法基于庞特里亚金极小值原理将最优控制问题转化为一个哈密顿边值问题;间接法收敛域小,求解精度较高,但间接法的求解过程同样较为繁琐。
文献[2-3]在离散时间控制系统中,根据动力学系统状态受控变化的规律,设计了时间约束下,基于状态转移的模型预测与反演控制(Model predictive and inversive control,MPIC)制导律。在MPIC制导中,是否可以通过减少推力器的工作脉冲以节省燃料是本文研究的内容。对于有k个控制周期的MPIC制导,将有2k种可能的推力器脉冲工作组合。以目前的算力,采用遍历法在庞大可行解空间进行燃料消耗寻优是难以实现的。因此,考虑采用智能搜索方法。
遗传算法模拟自然界的生物进化过程,根据基因交换、变异的遗传理论以及物竞天择、适者生存的自然选择规律,将优化问题转化成解集中目标适应度函数的评估以及最优解搜索问题,具有并行、高效、全局搜索和鲁棒性强等特点。遗传算法的主体是个体和种群。优化问题解集中的解被称之为个体,多个个体形成遗传种群。常见的遗传算法[4]有分层遗传算法、CHC算法、Messy遗传算法、自适应遗传算法、小生境遗传算法、并行遗传算法、混合遗传算法等等。遗传算法已被广泛应用于目标优化、自动控制、图像处理、机器学习等领域,并在旅行商问题求解[5]、任务调度[6-7]、供电优化[8-9]、机械臂控制[10-11]、航天器姿态控制[12-13]、星座设计优化[14-15]等各个方面得到研究和应用。在航天器的交会制导控制方面,国内外专家学者先后研究了在Lambert交会[16-17]、卫星任务规划[18-19]、深空探测轨道规划[20]、探月轨道设计优化[21-22]、空间轨道拦截[23-24]、在轨组装[25]、轨道上升与再入返回[26-27]等任务场景中采用遗传算法进行轨迹寻优。
采用遗传算法进行空间相对制导轨迹优化的常见方法,通常需结合推力器工作时点、工作方向、推力大小,对时间和轨控速度增量进行加权,以表示优化目标函数,在固定脉冲数次数的情况下,基于Lambert交会或C-W制导进行寻优。这些方法在优化结果中对交会制导精度缺少必要的分析,在优化过程中假设推力器以冲量形式工作,对于推力的工作次数未能进行充分地寻优。
本文基于MPIC多脉冲制导,构造以轨控速度总量为基础的适应度函数,以各控制周期中推力器是否工作设计二进制编码串形式的遗传个体,采用了等距稀疏控制的启发式种群初始化策略以提高计算效率。遗传交叉、变异以及选择淘汰策略形式简洁,优化结果全局收敛。针对能控性和推力器输出限制设计了罚函数以确保优化结果的可行性。给出了燃料寻优的一种智能搜索算法,为多脉冲交会制导的推力器最佳开、关机工作时机提供了寻优途径,同时保证制导的精度。
1 MPIC交会制导的燃料消耗寻优问题
地球近圆轨道上,参考航天器自由飞行,伴随航天器受控飞行于其附近,测控节拍时长为T。在参考航天器第二轨道坐标系下,两者之间的相对运动动力学在离散时间系统中可表示为[3]:
Xk=Gk,0X0+Qk,0Uk(0)
(1)
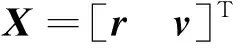
(2)
是无轨控情况下初始状态X0向kT时刻状态Xk演变的状态转移矩阵。
Qk,0=[Hk,k-1⋮Gk,k-1Hk-1,k-2⋮Gk,k-2Hk-2,k-3⋮
……⋮Gk,1H1,0]
(3)
为控制作用矩阵。Gj,i,Hj,i分别是状态i向状态j转移的状态转移矩阵和控制作用矩阵。
[ak-1,xak-1,yak-1,zak-2,x…a0,ya0,z]T
(4)
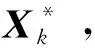
(5)
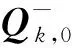
(6)
该控制序列确定了每个控制周期中的轨控加速度方向和大小。
当制导全过程所消耗燃料相对于航天器初始总质量相对较小,推力器比冲变化不大时,由式(4),可将相对制导的燃料消耗寻优等价于轨控速度的总量寻优,即
(7)
目前尚未见针对式(5)的精确解析寻优方法。因此,采用遗传算法进行推力器开关机的智能寻优。
2 遗传算法设计
2.1 构造适应度函数
遗传算法中的适应度函数需能对应和评估候选优化方案以指导选择淘汰过程。适应度函数应为单值、连续、非负函数,形式上应简单、易于计算,其值域应与搜索问题的解集对应。
在式(3)所示Qk,0中,将各控制周期所对应的矩阵分区分别赋值为全0或者加以保留,得到Q′k,0。则全0分区所对应的控制周期中,轨控加速度将为0,进而可以按照式(5)或(6)得到推力器开关机工作的轨控序列,并得到制导全过程所需的轨控速度总量。
由式(4)-(7),将轨控速度总量的倒数作为个体适应度函数
(8)
则适应度高的推力器开关机工作策略下,MPIC制导所需的轨控速度总量小。Q′k,0行满秩时,系统可控,Q′-k,0是系统动力学方程的解,MPIC制导理论上均可实现指定时间下的无偏控制且系统稳定。
当种群中各个体适应度的取值较为相近时,对适应度函数fi(i=1~N,N为遗传种群中个体数量)进行尺度变换,扩大个体之间适应度函数的相对差异以便于后续的择优选择。
(9)
式中:kf<1,kf→1。
当Q′k,0行不满秩时,式(5)、(6)没有可行解,系统不完全能控,对应的喷气序列不满足控制要求。采用罚函数法,对于Q′k,0行不满秩的个体,将其适应度函数直接设置为一个恒定的较小值,从而在选择环节将其淘汰。
工程上,推力器的输出有限。对于最大轨控加速度超限的情况,同样可以采用罚函数法将适应度函数直接设置为一个较小值。
2.2 种群个体设计
种群个体的具体编码形式应使其能参与适应度函数计算,并与各优化方案的评估值(适应度函数)相对应,同时又适合进行交叉、变异和优胜劣汰等遗传操作。在个体的编码方式上有二进制、整数、实数等不同的形式。其中,二进制编码便于交叉、变异等遗传操作。
根据前述适应度函数的构造原理,设计种群中的个体ci(i=1~N)为0、1二进制编码串形式。编码长度为相对制导控制周期数k,
(10)
根据个体编码中基因位ci,j(j=0~k-1)的0或1取值,由Qk,0得到控制作用矩阵Q′k,0。显然,以上编码方式满足遗传个体编码与推力器开、关机控制序列相对应的完备性、完整性和非冗余性。
2.3 选择淘汰
选择淘汰是遗传算法的核心关键步骤。每轮迭代中,通过适应度的评估对个体择优淘汰。种群朝着搜索空间中适应度更为优化的区域移动,因此遗传算法不是一种盲目的随机搜索方法,而是在适应度的指引下,具有明确搜索方向的启发式寻优方法。选择操作既要充分保留优良个体,同时又要维持群体的多样性以保持全局搜索能力。
采用比例选择方式。若种群中有N个个体,个体i的适应度为fi,其被选取的概率为
(11)
对个体按适应度从大到小排序,依次计算kp·N·Pi(kp≥1,为选取概率调节系数)并取整作为相应个体选取数量,依次排列后根据种群总量限制组成新的种群。适应度大的个体将被多次复制,适应度小的个体将被淘汰。
2.4 交叉变异
交叉算子按某种方式交换种群中个体编码串的部分基因位,从而形成新的个体,以便在解空间中进行有效搜索。交叉操作可以加速搜索过程,增强遗传算法的全局搜索能力。交叉操作有单点交叉、两点交叉、多点交叉、树交叉、部分匹配交叉等。在交叉操作中,交叉概率pc控制着交叉操作的频度。
本文采用两点交叉。遍历种群,按照交叉概率pc挑选个体。对选中的个体,在种群中随机挑选其他个体,随机选定二进制编码串中的两个基因位,将两个体编码串中两个基因位之间的基因段进行互换,从而完成交叉,形成两个新的个体。
变异操作可以保持个体基因的多样性,增强遗传算法的局部搜索能力,避免过早收敛。二进制编码串的变异通过基因位0、1之间的翻转实现。
本文设置变异概率pm。遍历种群,按照变异概率挑选个体。对选中的个体,在编码串中随机选择基因位进行0、1翻转操作,形成新的个体。
交叉和变异操作后,对原种群和新个体一并进行选择操作。保留原有个体可以避免在交叉、变异操作中损失掉最为优秀的个体,从而能同时保证算法的收敛性和全局性。每一代种群中,最优个体不会比上一代种群中最优个体差。
2.5 种群初始化
种群初始化直接影响遗传寻优过程。可以随机生成种群,也可以根据先验信息启发式初始化种群。种群个体数太少,则搜索空间中分布范围有限,有收敛于局部最优点的风险,一次遗传操作的寻优能力有限;种群个体数量过多,则一轮迭代中,适应度函数的计算次数增多,直接增加遗传寻优的计算复杂度。
交会制导的优化目的是通过减少推力器工作时间以节省燃料。按照推力器等距稀疏控制的启发式方法初始化种群。第1个个体二进制编码串所有基因位为全1,对应全时工作,其他第i个个体的各基因位按其序号j对i取模,余数为1时,将该基因位设置为1,否则为零,得到不同控制周期间隔下的稀疏控制个体:
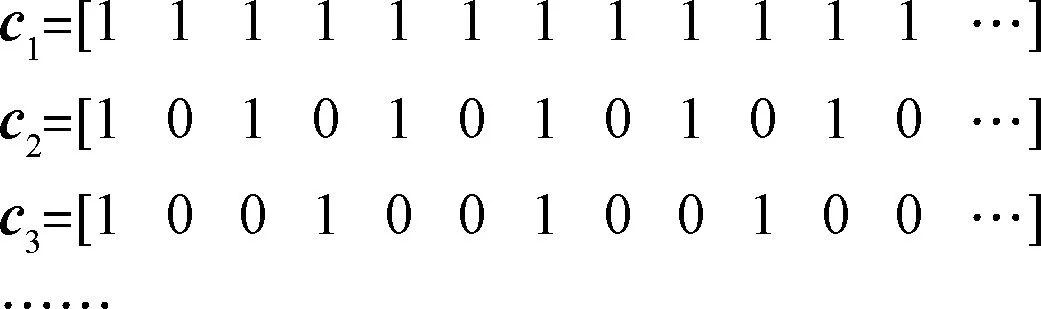
图1 种群初始化的启发式方法Fig.1 Heuristic initialization of population
遗传算法的寻优流程
步骤一:生成初始群体,设置交叉、变异概率等遗传参数;
步骤二:计算种群中各个体适应度;
步骤三:按照优胜劣汰的规则,増广优秀个体,控制种群规模,淘汰弱势个体;
步骤四:判断是否已达到优化停止条件,是则算法结束,否则进入下一步骤;
步骤五:以概率pc随机挑选种群中的个体,并在种群中随机挑选其他个体进行交叉操作,将新生成的个体加入种群;
步骤六:对种群中的个体以概率pm进行变异操作,将新生成的个体加入种群,返回步骤二。
算法结束条件:通过交叉、变异操作已无法找到更优的结果。
遗传算法搜索寻优流程如图2所示。
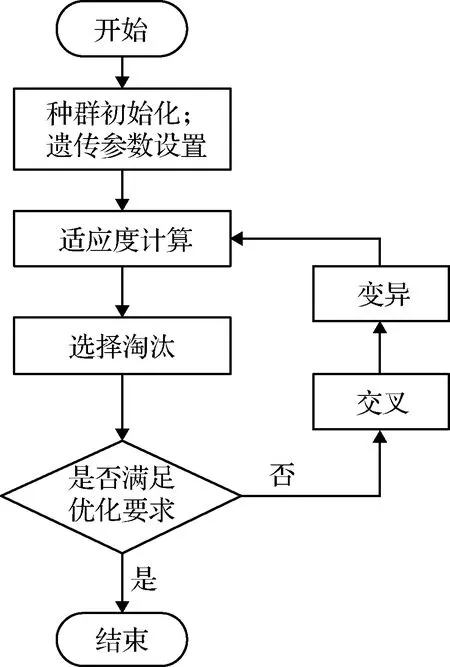
图2 遗传算法基本流程Fig.2 Basic flow of genetic algorithm
遗传算法在每一轮迭代中对种群中各个体进行适应度评估和择优选择,形成并行的搜索能力。其中的交叉变异策略使得搜索过程具有一定的跨度和跳跃性,在搜索过程中不易陷入局部最优,具有全局搜索能力。在应用中只需要种群个体及其适应度函数能覆盖优化问题的可行解并与之相对应,对适应度函数没有过多的约束和要求,因此遗传算法还具有较好的适应性和鲁棒性。
3 仿真校验
近圆轨道上两个航天器的初始轨道参数见表1。
初始相对位置为[12297.9836 m,18.288 m,-121.3913 m],初始相对速度为[0.3335 m·s-1,0.2366 m·s-1,0.2264 m·s-1]。期望实现零位置、零速度的交会对接。伴随航天器的采样控制周期为T=0.2 s,交会对接时间设置为1800 s,因此种群个体二进制编码串编码长度为9000。遗传种群个体设置为150个。交叉概率设置为0.6。变异概率设置为0.5。
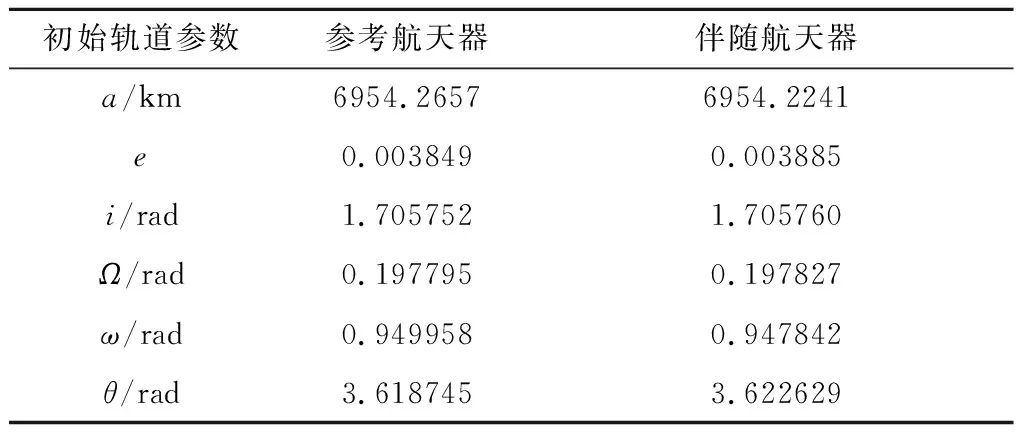
表1 轨道参数Table 1 Orbital parameters
分别采用随机和启发式方式生成初始种群。图3、图4分别给出了两种初始化策略下遗传迭代过程中最优个体所对应的推力器开关机工作状态。个体基因位取值为“1”表示相应控制节拍中推力器开机工作。基因位取值为“0”表示相应控制节拍中推力器不工作。
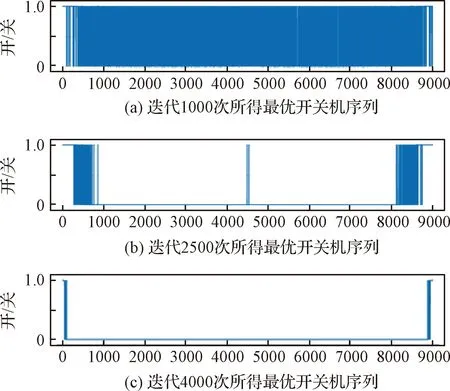
图3 种群随机初始化条件下最优个体对应的推力器开关机序列(1800 s)Fig.3 On / off sequence of thruster corresponding to the optimal individual of some generation in the case of randomly initialization(1800 s)
启发策略可以加速遗传算法寻优的过程。启发式初始化的种群经过1000次迭代寻优即可达到随机初始化种群遗传迭代4000次的类似寻优结果。
随着不断的遗传寻优,推力器的脉冲工作时间逐渐减少。本例最终优化得到:推力器在制导首、末两个控制周期内工作的双脉冲控制能在理论上实现燃料最优。
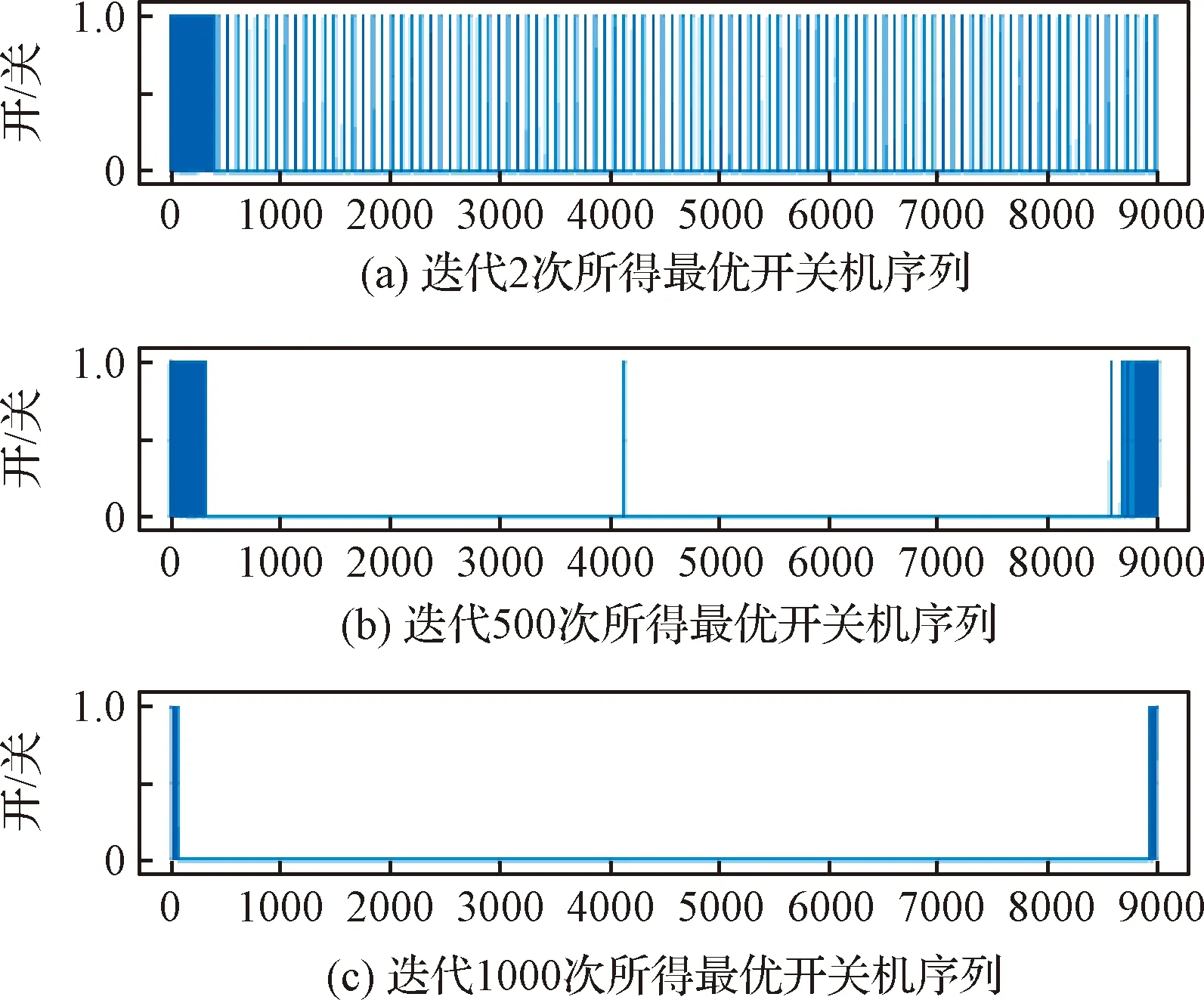
图4 种群启发式初始化条件下最优个体对应的推力器开关机序列(1800 s)Fig.4 On/off sequence of thruster corresponding to the optimal individual of some generation in the case of heuristic initialization (1800 s)
图5给出了各代最优个体对应的轨控速度总量理论值。作为对比,图5中还给出了随机初始化种群的最优个体的仿真校验结果。仿真校验中,模拟真实相对运动的动力学系统模型未经简化,MPIC制导律基于C-W方程,存在建模误差。若推力器工作时间过短,实际飞行轨迹将与模型预估产生较大偏差,实际轨控推力、轨控速度总量将偏离规划结果,制导误差增大;推力器工作更多脉冲,控制效果与规划结果更为一致,轨控加速度将更符合工程实际。
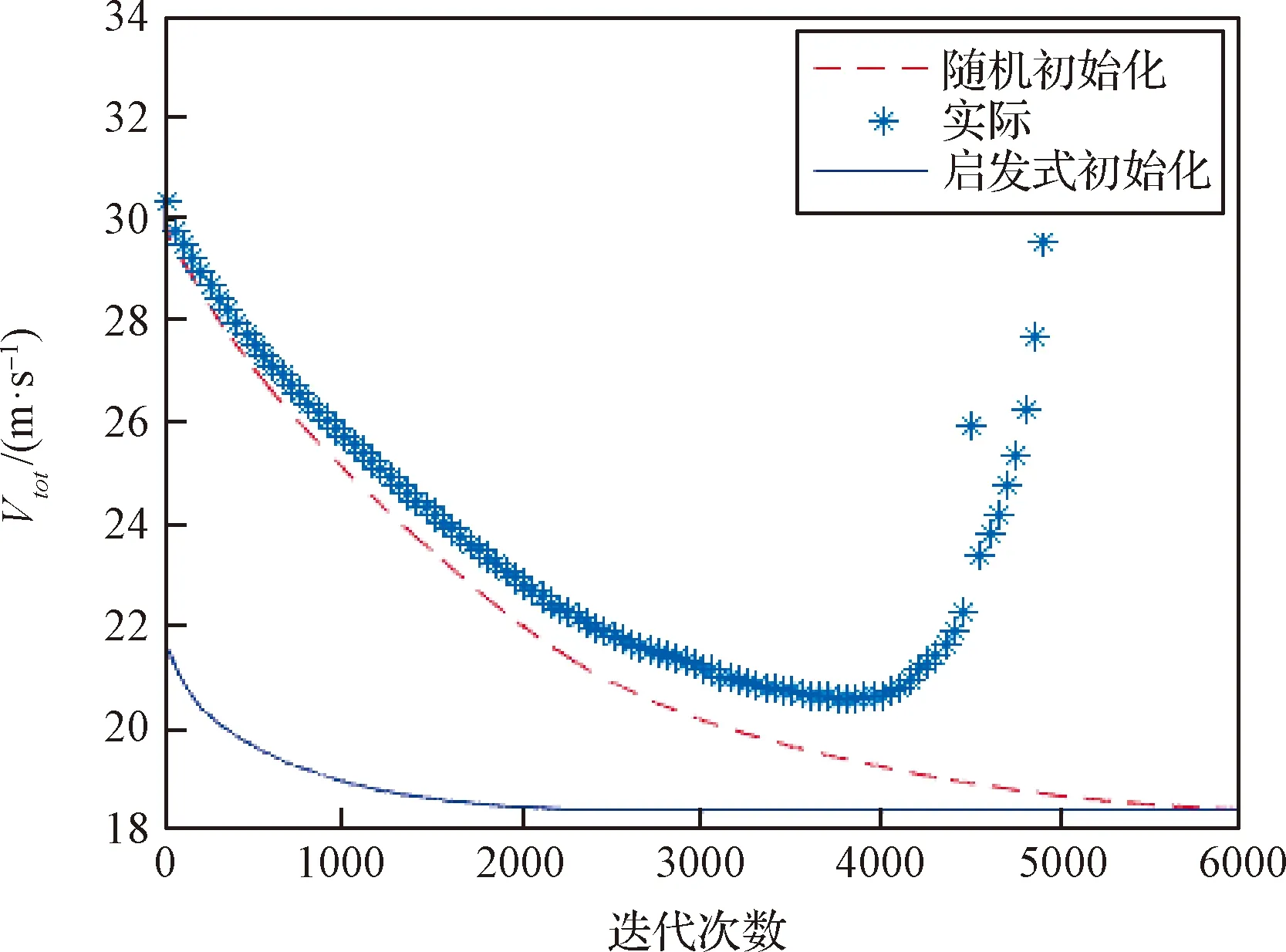
图5 各代种群中最优个体对应的轨控速度总量Fig.5 Velocity increment needed for orbit control corresponding to the optimal individual in each generation population
制导全过程时间不同,轨控推力器最佳工作时段的分布特征会有不同。图6给出了交会制导时间为6000 s时遗传算法寻优的结果,推力器工作的最佳时机大致可分为三个时段。
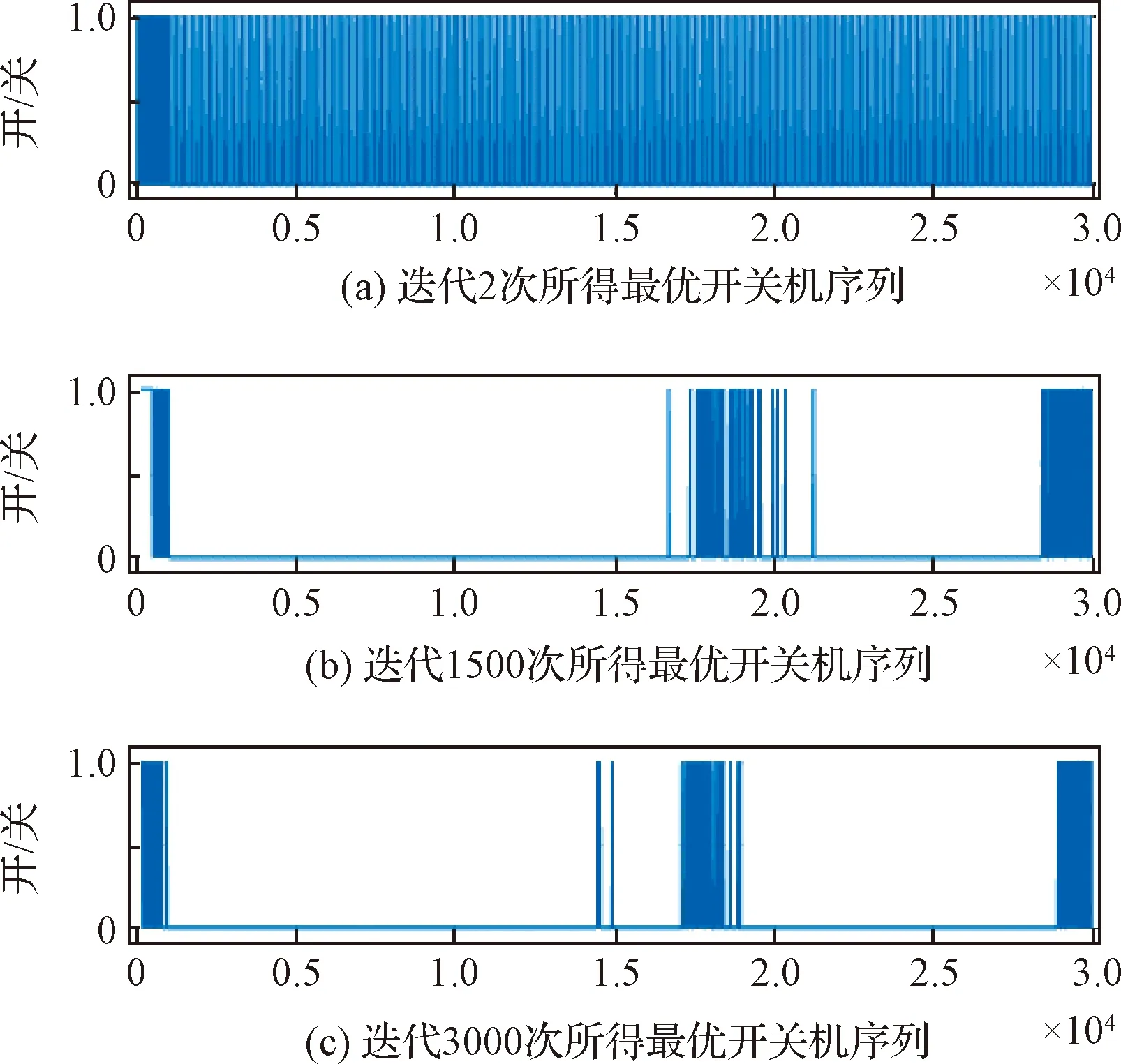
图6 种群启发式初始化条件下最优个体对应的推力器开关机序列(6000 s)Fig.6 On/off sequence of thruster corresponding to the optimal individual of some generation in the case of heuristic initialization(6000 s)
限定航天器最大轨控加速度为0.03 m·s-2,采用罚函数法以满足推力器输出约束,图7给出了根据寻优结果得到的轨控加速度,制导时间为1800 s。
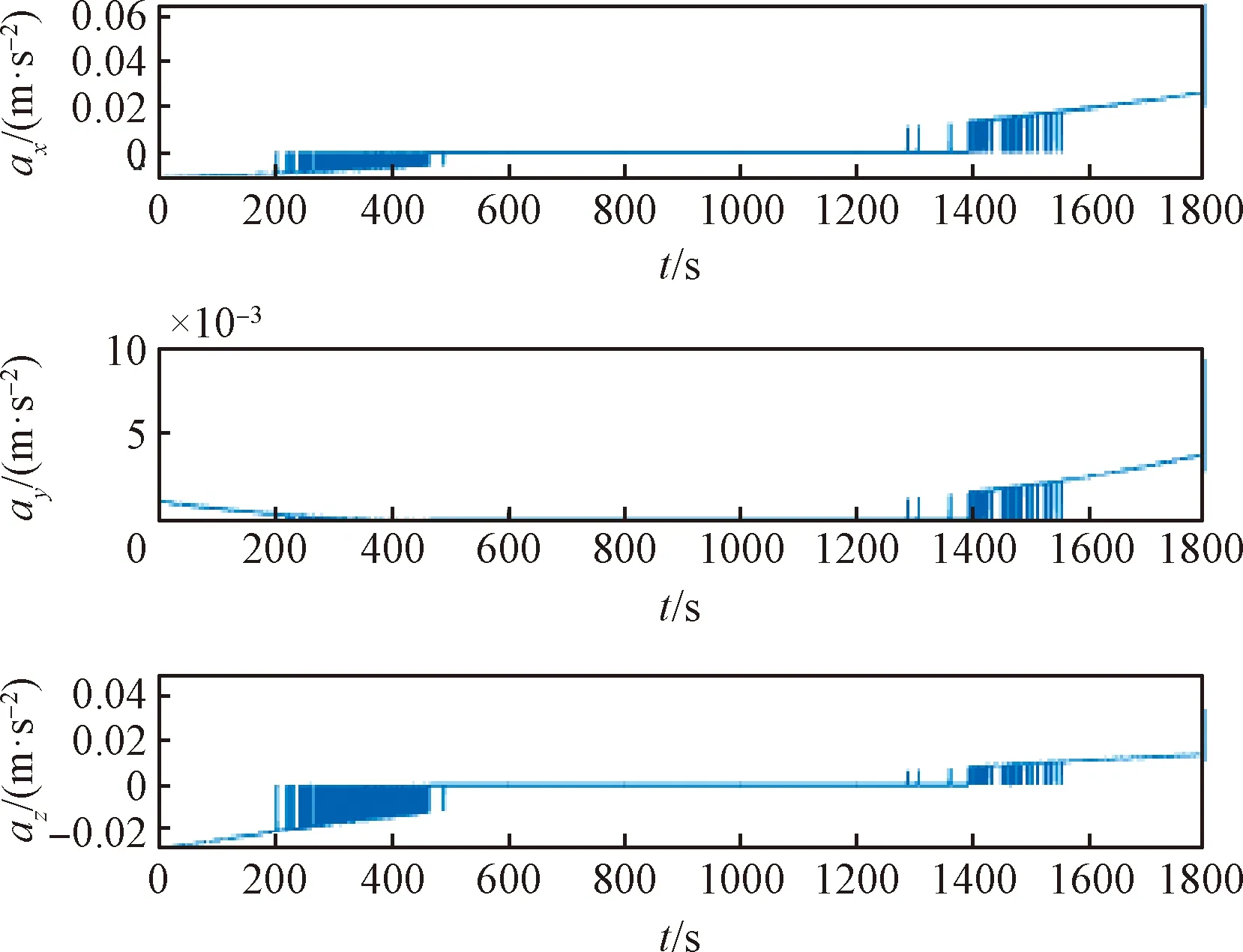
图7 推力输出约束下的轨控加速度Fig.7 Accaleration of orbit control with constraint of thruster output
种群随机初始化条件下,以遗传迭代4000次寻优(图3)得到的推力器最佳开关机序列进行MPIC交会制导,与推力器全时工作模式下的结果进行对比,三轴轨控加速度如图9所示。

图8 相对位置Fig.8 Relative position
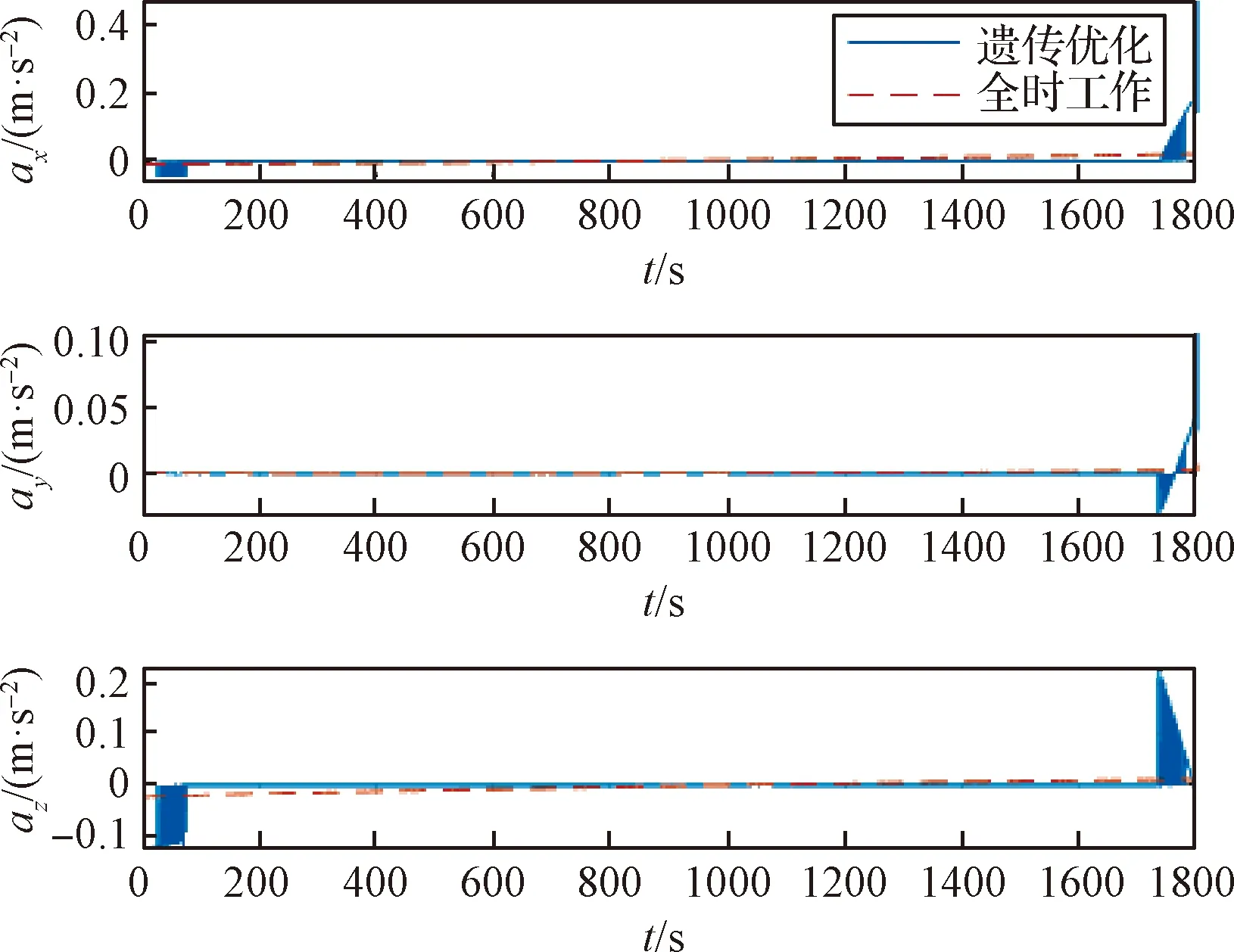
图9 三轴轨控加速度Fig.9 Acceleration of orbit control
制导结束时三轴相对位置、相对速度、最大轨控加速度以及所需的轨控速度增量见表2。
在优化得到的推力器工作模式下,相对制导的位置、速度精度仍然能达到与全时工作相当的精度,所需轨控速度总量则相较于全时工作模式减小约30%,制导过程中所需的最大轨控加速度稍大。
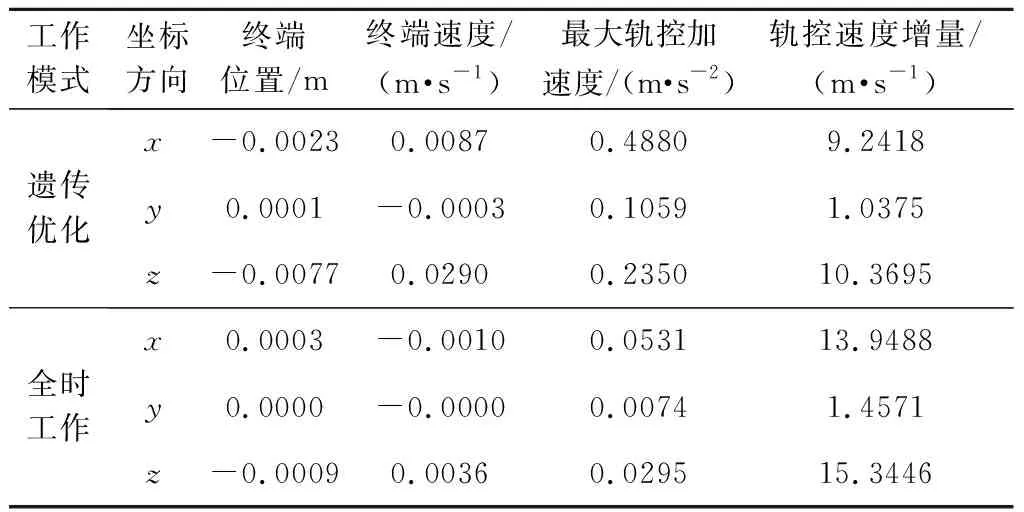
表2 交会制导结果Table 2 Rendezvous guidance results
4 结 论
通过将遗传优化算法与MPIC制导律相结合,可以较好地实现多脉冲制导过程中推力器最佳工作时机的寻优,减少航天器推力器的工作时间和燃料消耗,同时保证相对制导的精度。加速度形式的控制量可以等效换算为推力器的推力大小,易于工程实现。等距稀疏控制的种群初始化策略提高了遗传迭代寻优的效率。采用罚函数法可以保证系统的可控性并使推力器输出满足工程约束。优化得到的MPIC多脉冲制导工作模式具有较为显著的特征,能够为各类空间相对制导任务中制导律的设计提供较有意义和启发性的指导和参考。
个体二进制编码长度与相对制导的控制周期数对应,当控制周期数较多时,二进制编码长度与遗传搜索时间相应增加。遗传搜索过程对于计算能力仍有较高要求,在线实时应用仍然存在困难,后续可以采用自适应参数调整等策略进行优化,将遗传算法与其他局部收敛速度快的搜索方法相结合以达到更高的优化效率。

