不规则小行星附着可达区生成方法
黄美伊,梁子璇,崔平远
(1.北京理工大学深空探测技术研究所,北京 100081;2. 深空自主导航与控制工信部重点实验室,北京 100081)
0 引 言
小行星在科学研究、资源利用等方面具有独特价值,小行星探测不断吸引着各航天大国的关注[1]。随着探测任务从飞越/环绕探测向附着/采样探测的发展,表面附着相关技术正在成为小行星探测领域的研究热点[2]。在附着任务中,受探测器携带的燃料限制,小行星表面并非所有位置都是可以到达的。因此,小行星表面可达区的生成与分析在着陆点选取、任务规划等方面具有重要意义[3]。
可达区是指,探测器在给定初始条件及约束下所有能够到达的终端位置的集合;反之,在给定终端条件及约束下所有可行的初始位置/状态的集合构成可控区/能控集[4]。目前已有的可达区生成方法主要将地球和火星作为着陆对象,通过求解一系列轨迹优化问题进而得到可达区边界[5-11]。针对再入飞行器可达区生成问题,Saraf等[7]采用最大/最小阻力加速度剖面加权插值得到了一系列飞行轨迹,并由最大横程和最大纵程轨迹的终端点生成了可达区边界;汪雷等[8]采用高斯伪谱法对飞行器射程最值问题进行优化求解,分别得到了可达区的远近边界;赵江等[9]将倾侧角剖面参数化,并利用粒子群算法优化求解,通过生成倾侧角指令集合实现了可达区快速求解。针对火星着陆的可达区问题,Benito等[10]系统地研究了可控域和可达域,通过网格检测的方法获得了可达区,并定义了考虑终端高度、动压等指标的评估函数,对可达区内的点进行了量化评估;赵泽端等[11]在求解极限航程与极限开伞高度问题的基础上,通过构造合适的同伦参数延拓出纵向可达区,提升了求解效率。
小行星附着方面的研究,目前主要围绕轨迹规划[12-15]与制导控制[16-19]等方面开展,而表面可达区的相关研究未见公开报道。与地球或火星相比,小行星表面可达区的生成具有以下难点:首先,小行星表面不规则会导致终端位置约束不连续,直接优化轨迹存在不收敛的问题;其次,小行星形状不规则、引力场不均匀,可达区通常会呈现出较为复杂的形状,而求解精度要求高,故面临着求解过程复杂、求解效率低的问题。此时,若将地球、火星的可达区求解方法(如文献[8]中的高斯伪谱法)直接应用于小行星,计算时间将大幅增加,难以满足任务需要。因此,为获取小行星表面的可达区,必须结合其不规则特性研究专门的求解方法。
本文针对不规则小行星表面附着任务,提出了一种可达区生成方法。为解决小行星附着轨迹终端位置约束不连续问题,建立了经纬度坐标与质心距的非线性映射函数,以提高优化问题的收敛性;为解决复杂可达区边界生成问题,提出了一种动态邻域搜索策略,将可达区边界生成问题转化为附着基准点计算、边界起点计算和边界点搜索生成三个子问题。针对边界点的搜索问题,设计了导向式动态邻域搜索方法,将复杂约束下的非定点着陆优化问题简化为定点着陆燃耗优化与边界插值问题,提高了优化求解效率。最后,以小行星433 Eros为对象进行了仿真分析,验证了所提出方法的有效性。
1 动力学与约束模型
以小行星的质量中心为坐标原点O建立小行星固连坐标系Oxyz,以最大惯量轴即小行星自旋轴方向为z轴,最小惯量轴方向为x轴,y轴与x轴、z轴共同构成右手坐标系。定义探测器状态变量
(1)
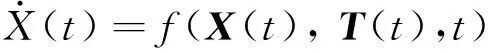
(2)
式中:ω为小行星自旋角速度;gx,gy,gz分别为三轴引力加速度;g0为地球海平面引力加速度大小;Isp为探测器发动机比冲;Tx,Ty,Tz分别为探测器推力矢量T在三轴方向上的投影。令Tmax为探测器最大推力,则探测器附着过程中受到推力约束
(3)
在初始时刻t0,探测器状态变量已知为X0,则
X(t0)=X0
(4)
在终端时刻tf(一般不做约束),探测器状态变量受到位置、速度、质量三类约束。可达区生成问题中,终端位置坐标不固定,只要求探测器到达小行星表面即可。对于形状不规则的小行星,通常用多面体对小行星形状进行建模,并采用拉普拉斯算子判断探测器在小行星内部、外部还是表面[20]:
(5)
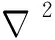
Φ(x(tf),y(tf),z(tf))=2π
(6)
为使探测器实现小行星表面“软着陆”,终端速度需满足以下约束
(7)
此外,考虑到探测器燃耗有限,终端质量需满足
m(tf)≥mnet
(8)
式中:mnet为不含燃料的探测器质量,即探测器净质量。
2 可达区生成方法
探测器着陆可达区可视为满足一定约束的终端位置的集合,为便于描述终端位置,取探测器位置变量Y为状态变量X的投影
(9)
式中:I3×3为三阶单位矩阵;03×4为零矩阵。当t=tf时,Y(tf)即为终端位置变量。
小行星表面可达区U受到式(2)描述的动力学约束、式(3)描述的推力约束、式(4)描述的初始状态约束及式(5)-(8)描述的终端状态约束,可表示为Y(tf)的集合
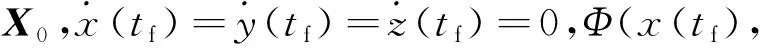
y(tf),z(tf))=2π}
(10)
式中:R3表示三维向量空间。
2.1 终端约束处理
在可达区生成过程中需要多次对附着轨迹进行优化。受到小行星表面极不规则特点的影响,优化问题中的探测器终端位置变量无法通过固定轨道高度直接进行约束,通常采用阶跃函数式(5)进行判定,但其不连续性不适用于轨迹优化问题。
针对终端位置约束不连续的问题,本文引入随经纬度变化的径向高度对其进行有效约束。首先,基于已知的小行星表面点数据得到各点质心距关于经纬度坐标的映射关系R(θ,φ)。定义探测器所在位置质心距r(t)与对应坐标表面点的质心距差值为径向高度re(t),则探测器终端位置约束表达为连续形式
re(tf)≜r(tf)-R(θ(tf),φ(tf))=0
(11)
进而,结合式(10)可得
(12)
求解集合U即得到小行星表面可达区。
2.2 可达区生成策略
在有限燃耗条件下,探测器附着所需燃耗最小的点应位于可达区内部;而对于可达区边界上的点,则需燃料耗尽才能到达(后文简称为极限燃耗点)。因此,本文以最小燃耗点为附着基准点,通过搜索极限燃耗点来获取可达区边界。
在小行星固连坐标系Oxyz下对着陆点L相对附着基准点P0的位置进行描述,如图1所示。已知附着基准点P0坐标后,可用角度α,β描述着陆点L相对P0的方位,其中α为LP0与基准经度线的夹角,β为OP0与OL的夹角。于是,可达区的边界求解问题可以描述为求解不同α方向上,有限燃耗下探测器所能到达最大质心角βmax的着陆位置。对于给定的着陆点,令探测器实现附着的最小燃耗为Cmin(α,β),则有
Cmin(α,βmax)=m0-mnet
(13)
式中:m0表示探测器初始时刻质量;m0-mnet表示探测器最大可用燃耗,即初始时刻所携带的全部可用燃料。
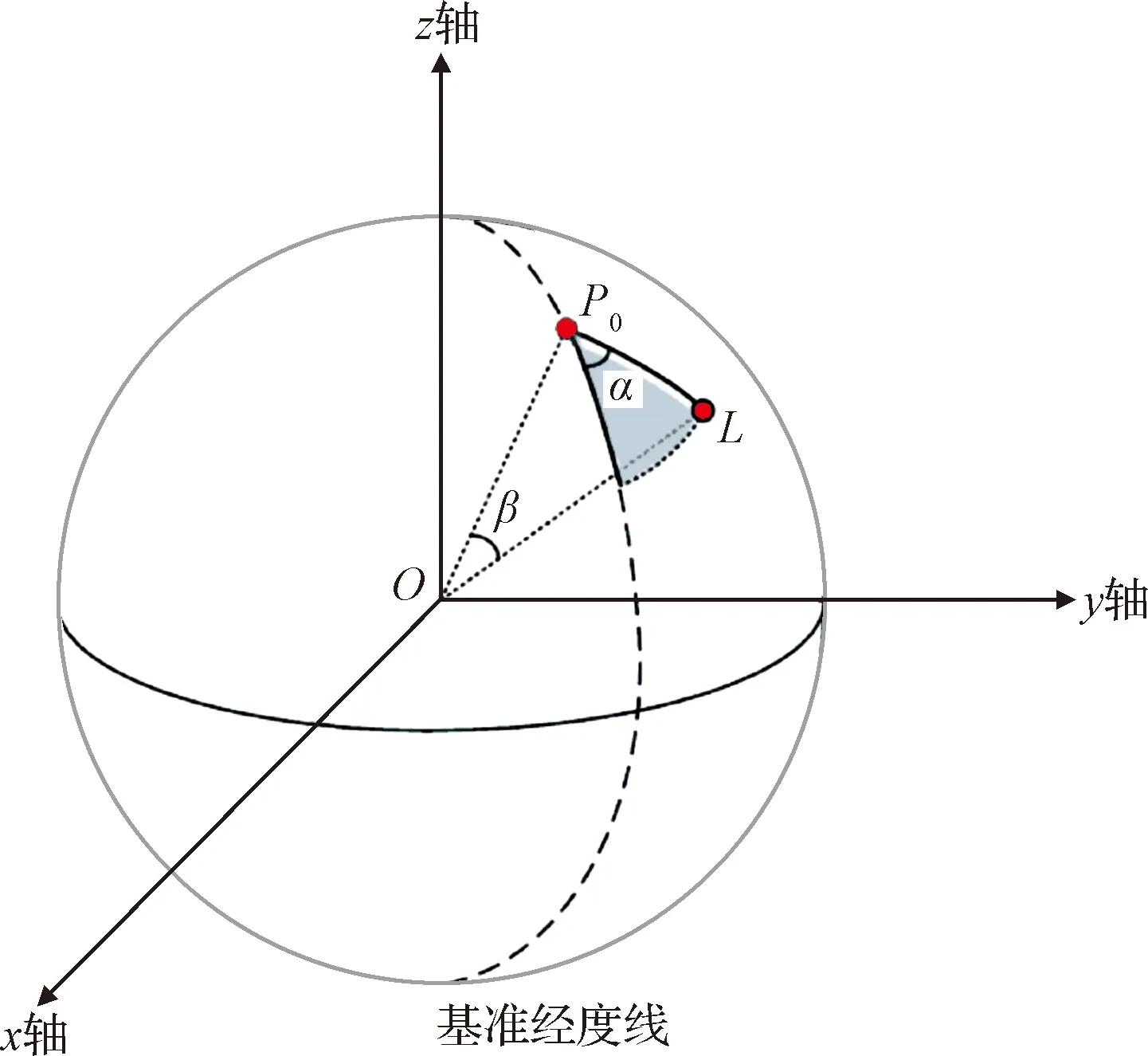
图1 着陆点坐标示意图Fig.1 Illustration of the coordinate of the landing site
围绕附着基准点求解各方向上的βmax得到可达区边界。对于给定的方向角α,相应的优化问题如下
(14)
式中:最后一项为角β受到的约束,与终端位置的经度、纬度、方向角α相关。Λ(θ,φ,β)的计算公式如下:
Λ(θ,φ,β)=[cosφcos(φ0-β)cos(θ-θ0)+
(15)
式中:θ0,φ0分别为附着基准点所在经度与纬度。在不同方向上求解βmax,得到一系列可达区边界点,构成可达区边界。但式(14)和(15)表明,优化对象β受到与终端位置经度、纬度相关的复杂三角函数约束,因此,优化问题的求解过程较为复杂。
为简化可达区求解过程,减少复杂优化问题的求解次数,本文采用一种邻域搜索的可达区生成策略,基本步骤如下:
1)求解最小燃耗轨迹优化问题,得到附着基准点,并选取角度α0作为起始点方向;
2)求解式(14)所示极限燃耗轨迹优化问题,得到α0方向上β=βmax的着陆点作为边界起始点;
3)从起始点出发,采用动态邻域方法,求解其余α方向上的可达区边界点。
2.3 边界起始点生成
2.3.1附着基准点计算
为求解附着基准点,以燃耗最小为优化目标,并考虑式(12)描述的各项约束条件,建立最小燃耗轨迹优化问题如下
(16)
可采用高斯伪谱法求解上述轨迹优化问题,得到着陆所需最小燃耗Cmin0。此时,存在以下三种情况:
1)Cmin0>m0-mnet时,探测器无法实现软着陆,U为空集;
2)Cmin0=m0-mnet时,探测器只能在P0完成软着陆,故可达区U= {P0};
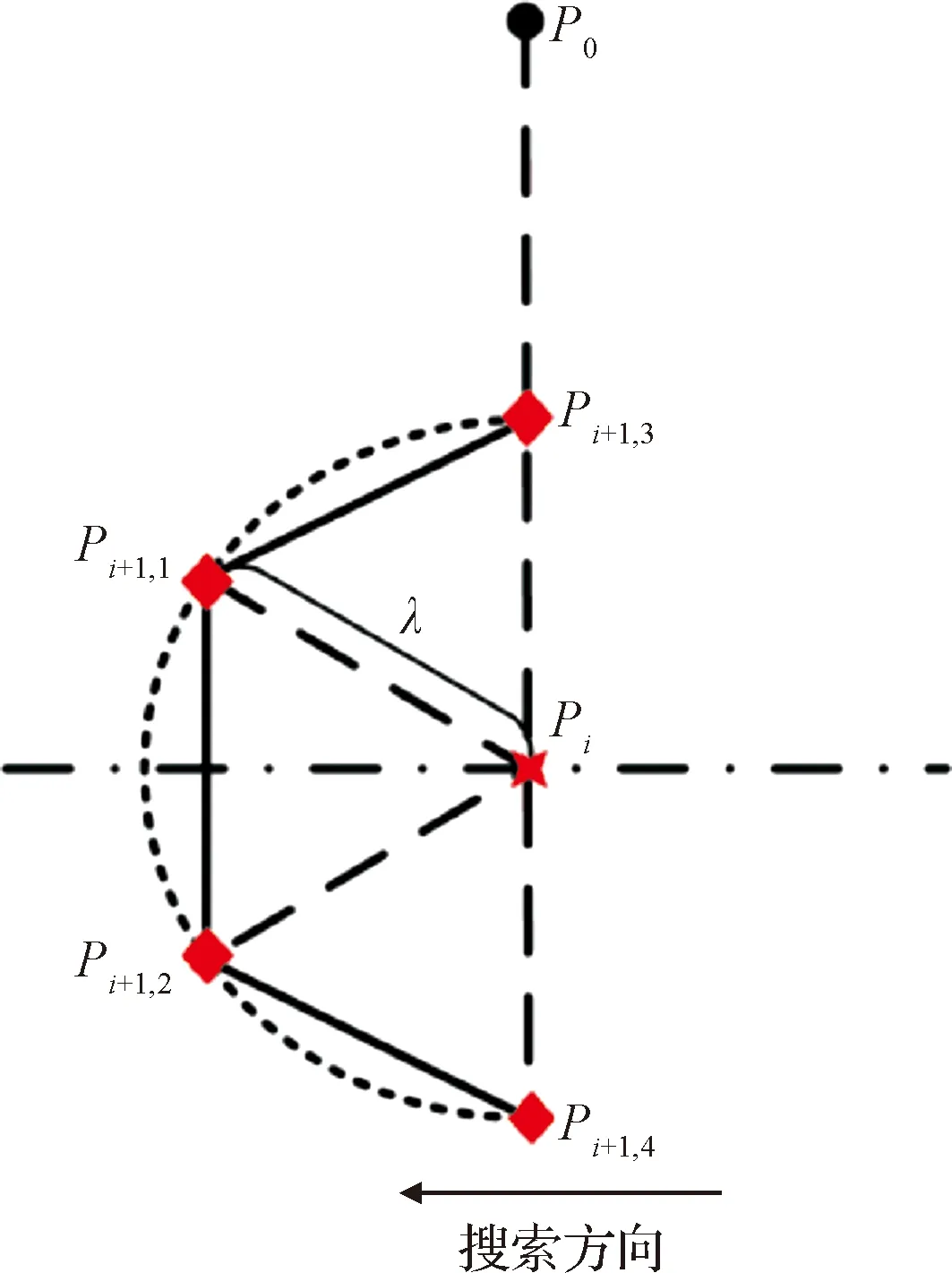
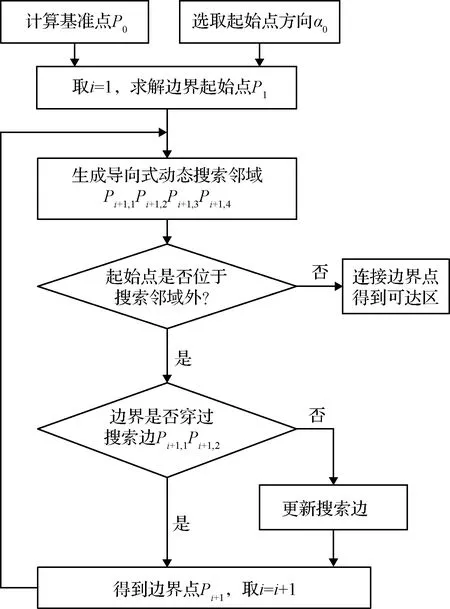
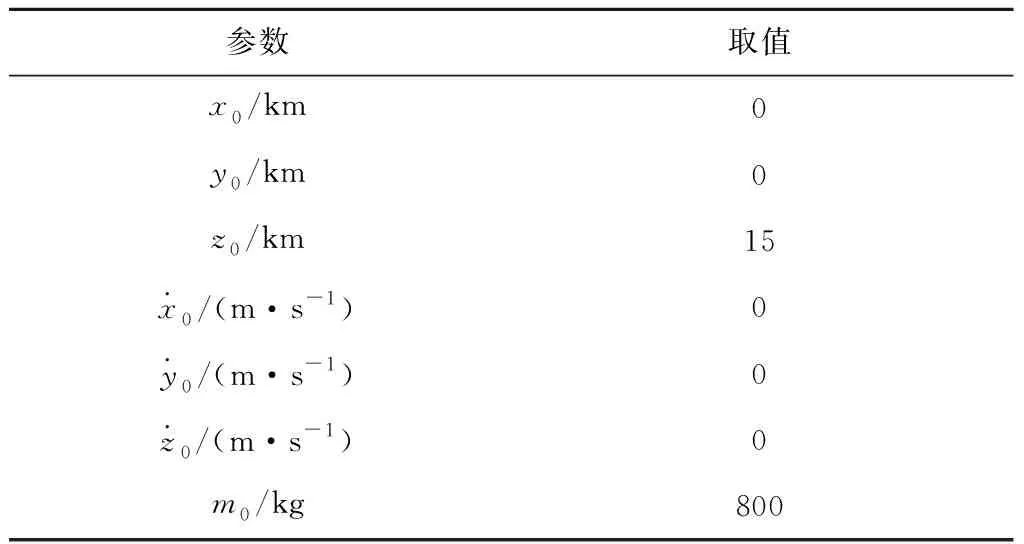
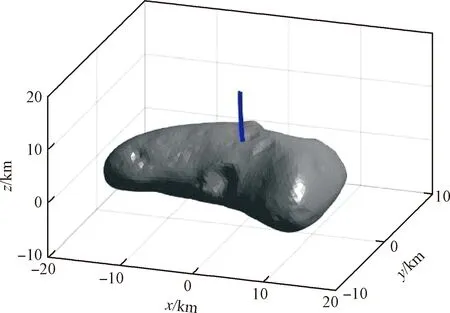
3)Cmin0 对于第三种情况,P0即为附着基准点。 2.3.2边界起始点计算 以P0为基准点,优化α0方向上的βmax得到边界起始点。本文取α0为零,求解优化问题 (17) 得到该方向上βmax及边界起始点P1。 可达区邻域搜索的基本思想是:当已知某一边界点后,在其附近生成邻域,并对邻域内的点进行搜索以确定下一边界点,之后再对下一边界点进行邻域搜索,最终得到可达区边界。为简化搜索过程,定义第i步搜索邻域为:以搜索中心点Pi为圆心,朝向搜索方向半圆的内接半六边形。其顶点为搜索点Pi+1,1-Pi+1,4,如图2所示。其中,搜索方向垂直于附着基准点P0与搜索中心点Pi的连线,并在搜索过程中随Pi动态变化。搜索点Pi+1,1-Pi+1,4与中心点Pi具有以下几何关系 图2 搜索邻域示意图Fig.2 Illustration of search neighborhood (18) 式中:λ为搜索步长;(αi,βi)为中心点Pi坐标;(αi+1,j,βi+1,j)为搜索点Pi+1,j的坐标(j=1, 2, 3, 4)。 第i步搜索过程中,首先取Pi+1,1Pi+1,2为搜索边,将两端点Pi+1,1与Pi+1,2的坐标代入R(θ,φ)计算其三轴位置变量xt,yt,zt。进而,将三轴位置变量作为终端约束求解以下定点着陆的轨迹优化问题 (19) 假设Cmin,1与Cmin,2分别为Pi+1,1与Pi+1,2点对应的最小燃耗。若满足 [Cmin,1-(m0-mnet)][Cmin,2-(m0-mnet)]≤0 (20) 则表示可达区边界穿过搜索边Pi+1,1Pi+1,2。于是,通过对点Pi+1,1与Pi+1,2坐标进行插值得到搜索结果Pi+1点为 (21) 若式(20)不满足,则需将搜索边更新为Pi+1,1Pi+1,3或Pi+1,2Pi+1,4。用Pi+1, jPi+1, j+2表示更新后的搜索边,由燃耗Cmin,1与Cmin,2确定的更新逻辑为 (22) 之后,重新求解式(19)描述的定点着陆轨迹优化问题,得到两个搜索点的最小燃耗。进而,可采用类似方法由Pi+1,j与Pi+1, j+2的坐标插值求解Pi+1点坐标。 基于邻域搜索的可达区生成流程如图3所示。得到边界起始点之后,从该点出发,通过动态邻域搜索下一边界点;沿顺时针方向绕基准点对可达区边界进行搜索,直到边界起始点位于当前搜索邻域内;最终,得到的边界点首尾相连即构成可达区边界。 图3 可达区生成流程图Fig.3 Reachable zone generation scheme 以小行星433 Eros为例,对可达区生成方法进行仿真验证。小行星自旋角速度ω=3.3117×10-4rad/s;探测器净质量mnet= 797.5 kg;最大可用燃耗为2.5 kg;发动机比冲Isp= 300 s;推力最大值Tmax= 25 N;考虑探测器初始时刻在小行星北极点上空悬停,设定初始状态见表1。可达区边界进行动态邻域搜索时,取步长λ=10°。 表1 探测器初始状态Table 1 Initial conditions of the vehicle 以燃耗最优为性能指标函数,求解非定点附着轨迹优化问题。优化可得,小行星软着陆所需的最小燃耗为Cmin0= 2.03 kg,对应的附着基准点坐标为(θ0,φ0) = (57.91°, 86.83°)。该点位于小行星北极点附近,相应的附着轨迹如图4所示。 获得附着基准点后,求解得到边界初始起始点经纬度坐标(57.91°, 55.53°),进而利用邻域搜索方法获得可达区边界,其在Oxy平面上的投影如图5所示。在以小行星北极为极点,零经度方向为极轴的极坐标系下,可达区边界如图6所示。受到小行星形状及引力场的影响,可达区边界呈现出不规则形状。图6中标明了每一步搜索时采用的4个搜索点。不难发现,每次搜索确定的下一个边界点大多位于Pi+1,1Pi+1,2上,只有点(153.33°, 56.86°)位于Pi+1,2Pi+1,4上,相应地,可达区边界在该点处出现了较大的转角。当搜索边为Pi+1,1Pi+1,2时,只需求解2次定点着陆轨迹优化问题,而当搜索边为Pi+1,2Pi+1,4时也仅需增加1次优化问题求解。因此,仿真结果表明,所提出的邻域搜索方法具有较高的求解效率,且对不规则边界具有自主调整搜索方向的能力。 在邻域搜索方法中,为了提升可达区边界生成效率,每次只优化求解搜索点对应的附着轨迹,并由搜索点数据插值得到下一边界点。为检验所得到的边界点是否满足燃耗要求,以边界点坐标为终端约束重新优化求解相应的最小燃耗轨迹,结果如图7所示。将各边界点对应的最小燃耗与探测器的最大可用燃耗进行比较,百分比误差如图8所示。可以看出,误差在0.6%以内,表明邻域搜索方法得到的可达区边界具有较高的精度。 图4 小行星表面最小燃耗附着轨迹Fig.4 Fuel-optimal landing trajectory on asteroid surface 图5 小行星表面可达区边界Fig.5 Reachable zone boundary on asteroid surface 图6 极坐标下可达区边界Fig.6 Reachable zone boundary in polar coordinates 图7 可达区边界点对应的着陆轨迹Fig.7 Landing trajectories for boundary points of reachable zone 图8 可达区边界点的燃耗误差Fig.8 Fuel consumption error for boundary points of reachable zone 需要指出,在不考虑计算效率的情况下,可达区也可以通过求解式(14)描述的轨迹优化问题得到,即直接求解不同α方向上β的最大值。为与邻域搜索法进行对比,将文献[8]中的高斯伪谱法用于求解式(14),并称之为直接优化法。采用直接优化法在相同的初始条件及环境条件下生成可达区边界,并与邻域搜索法的结果对比,如图9所示。不难发现,两种方法求解得到的可达区边界几乎重合,表明邻域搜索获得了较为准确的边界。 图10表示邻域搜索法与直接优化法耗时的百分比。在边界起始点方向(经度为57.91°),两种方法的求解过程一致,因此所耗时间相等;在其余方向,采用邻域搜索法的耗时不到直接优化法的10%。综合而言,本文所提出的邻域搜索法能减少90%以上的求解时间,大幅提升了求解效率。 图9 两方法的可达区边界对比Fig.9 Reachable zone boundaries for two methods 图10 邻域搜索法与直接优化法的耗时比Fig.10 Percentage computational cost of proposed method over conventional one 对于给定的小行星对象,可达区主要与探测器初始位置及燃耗相关。为验证可达区生成方法的适应性,并分析可达区的影响因素,对不同初始位置及燃耗条件下的可达区进行仿真。首先,考虑初始时刻探测器悬停点质心距的改变,在15 km基础上,依次增大至16 km和减小至14 km,生成相应的可达区边界。图11对比了三种初始位置下的可达区边界,不难发现,可达区大小受初始位置影响,但其形状变化不大。初始位置越高,相应的可达区范围越小,这是由于距小行星越远,实现附着所需燃耗越大。 接下来,考虑燃耗条件变化,在2.5 kg基础上取最大可用燃耗分别为2.4 kg与2.6 kg,得到的可达区边界如图12所示。结果表明,可用燃耗增大时,探测器可机动范围增大,可达区也随之扩大,相比于初始位置,燃耗对可达区的影响更为明显。仿真结果表明,本文给出的导向式动态邻域搜索方法适用于不同初始位置、燃耗条件下的可达区生成。 图11 不同初始位置下可达区边界Fig.11 Reachable zone boundaries for different initial positions 图12 不同燃耗下可达区边界Fig.12 Reachable zone boundaries for different fuel consumptions 本文针对不规则小行星表面的可达区生成问题,提出了一种基于动态邻域搜索的生成策略。建立了质心距映射函数,对非定点附着的终端位置约束进行了处理,保证了不规则表面轨迹优化问题的收敛。在此基础上,将可达区生成问题分解为附着基准点计算、边界起点计算和边界点搜索三个子问题分别求解,简化了问题约束,实现了不规则小行星表面可达区的生成,并提高了求解效率。以小行星433 Eros为对象,进行了可达区仿真与适应性分析。结果表明,所提出的可达区生成方法能够求解探测器在有限燃耗条件下、不规则表面的可达区,并适用于不同的初始位置和燃耗条件;可达区范围随初始位置的上升而减小,随可用燃耗的增大而增大;所提出的导向式邻域搜索方法具有较高的求解效率,每次搜索过程的定点着陆轨迹优化问题求解数量不超过3个,在本文第3节中给出的仿真条件下,耗时比直接优化法减少90%以上。2.4 可达区边界邻域搜索
3 仿真分析
3.1 可达区仿真结果
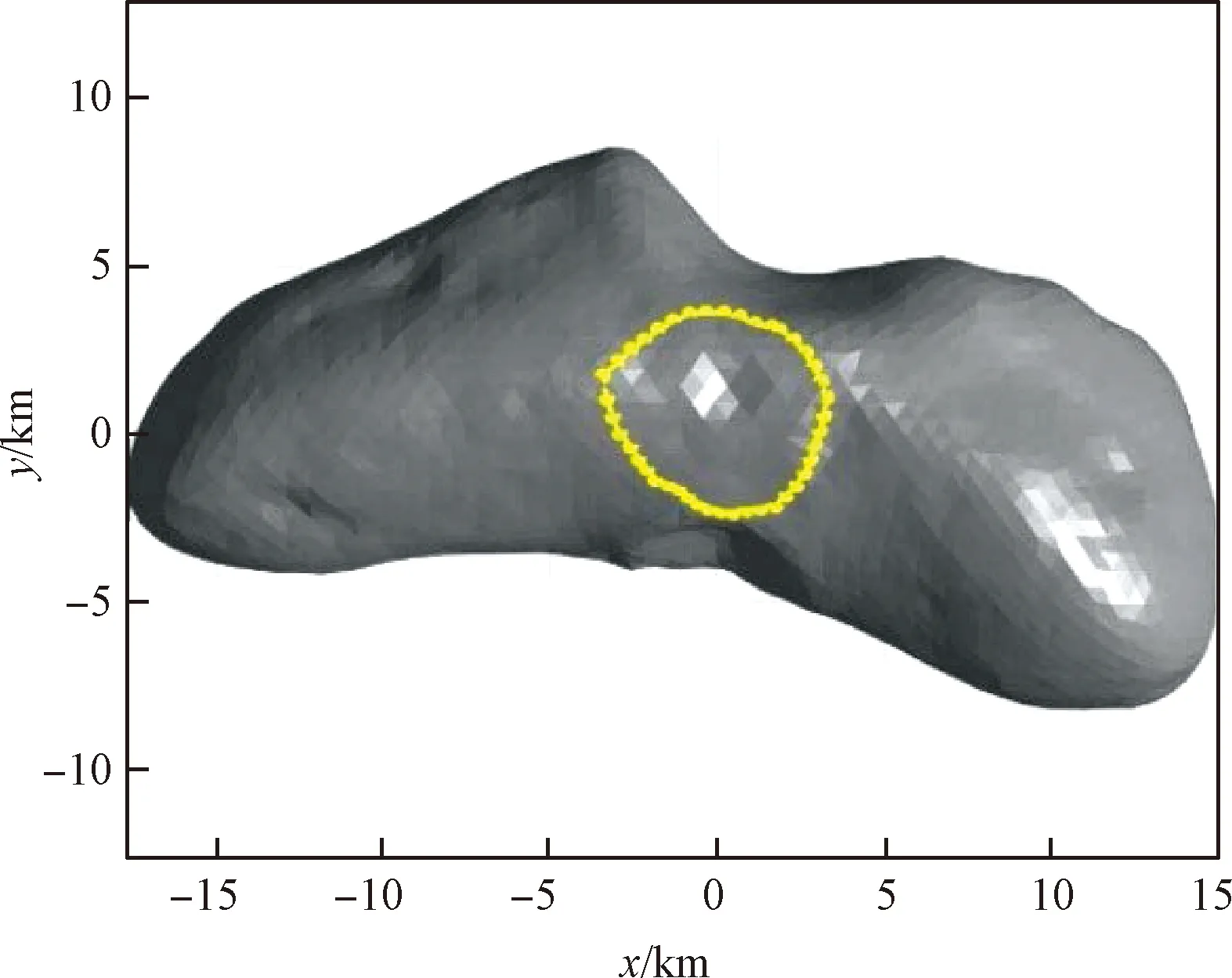
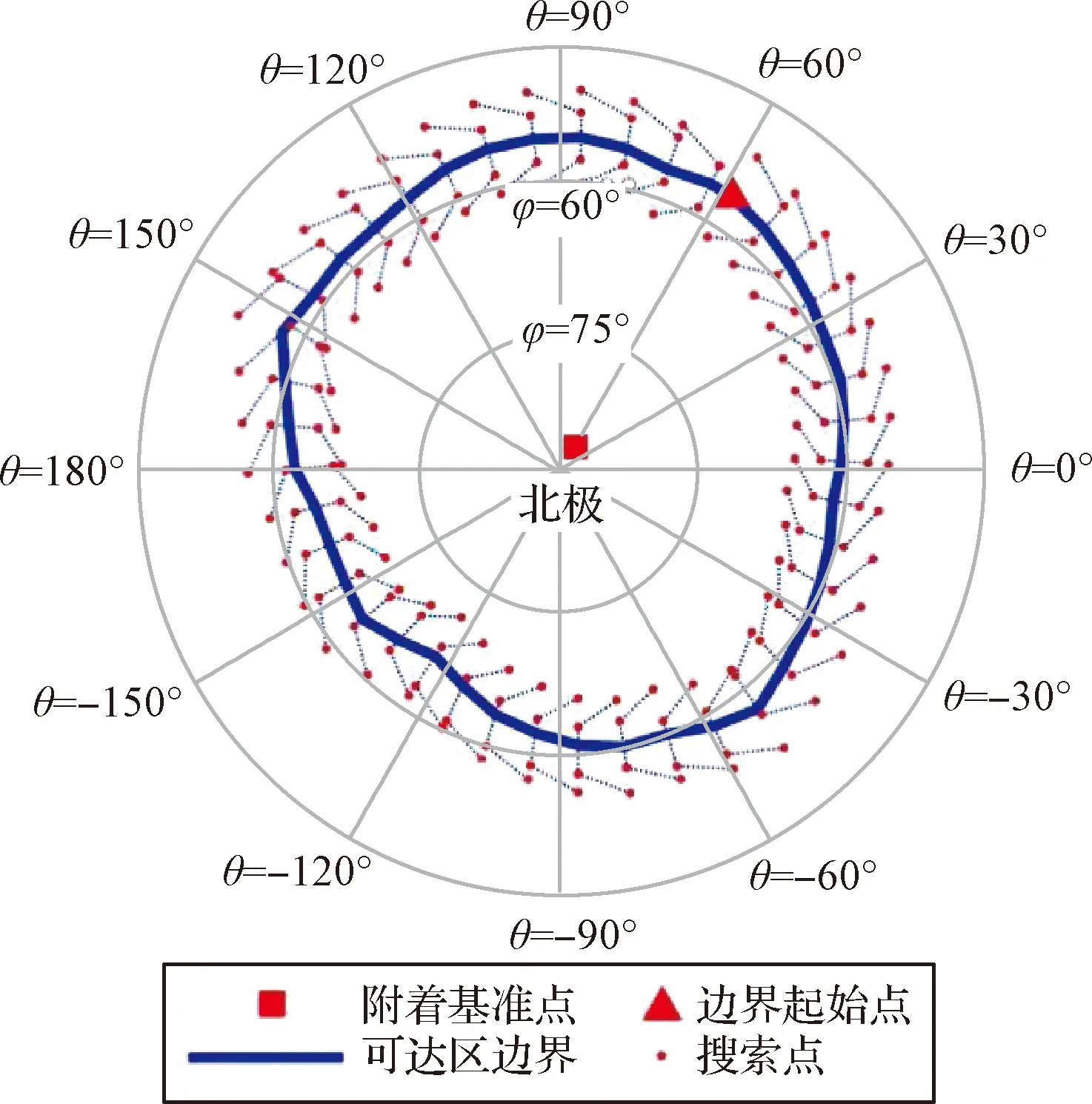
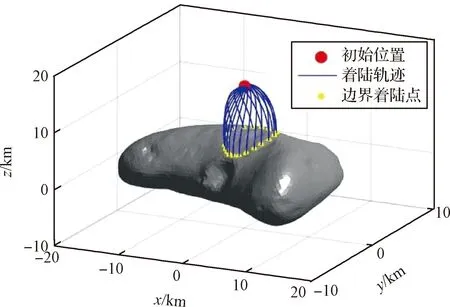
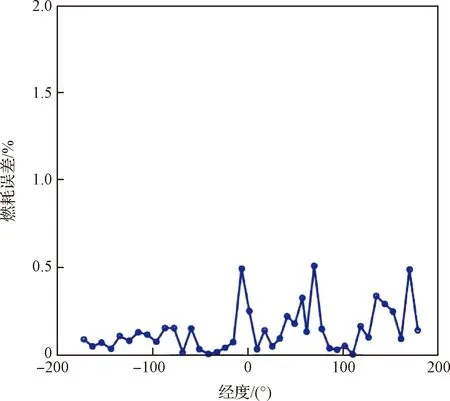
3.2 可达区生成方法对比
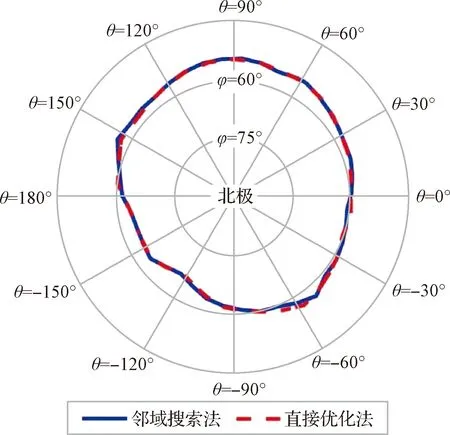
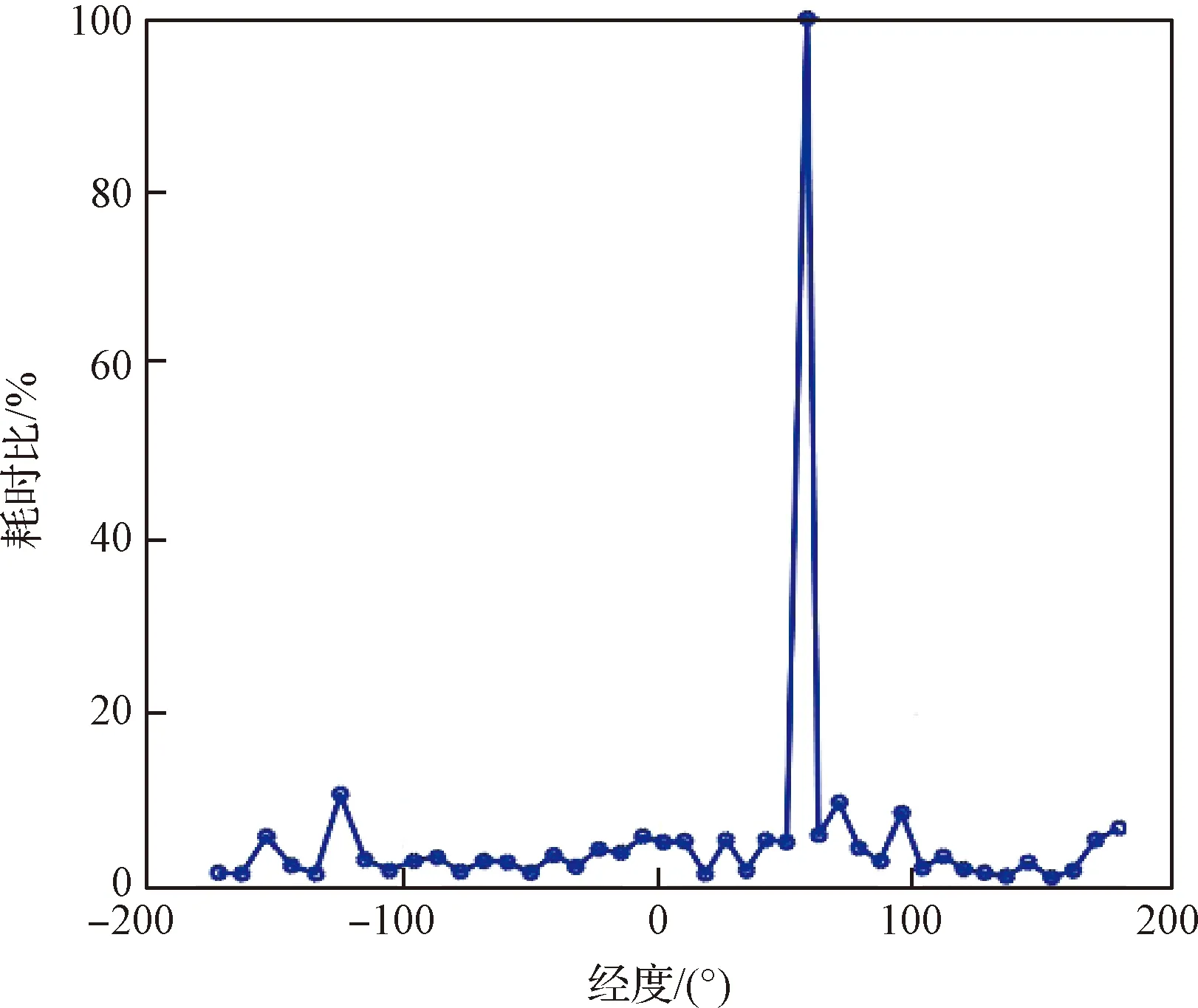
3.3 方法适应性分析
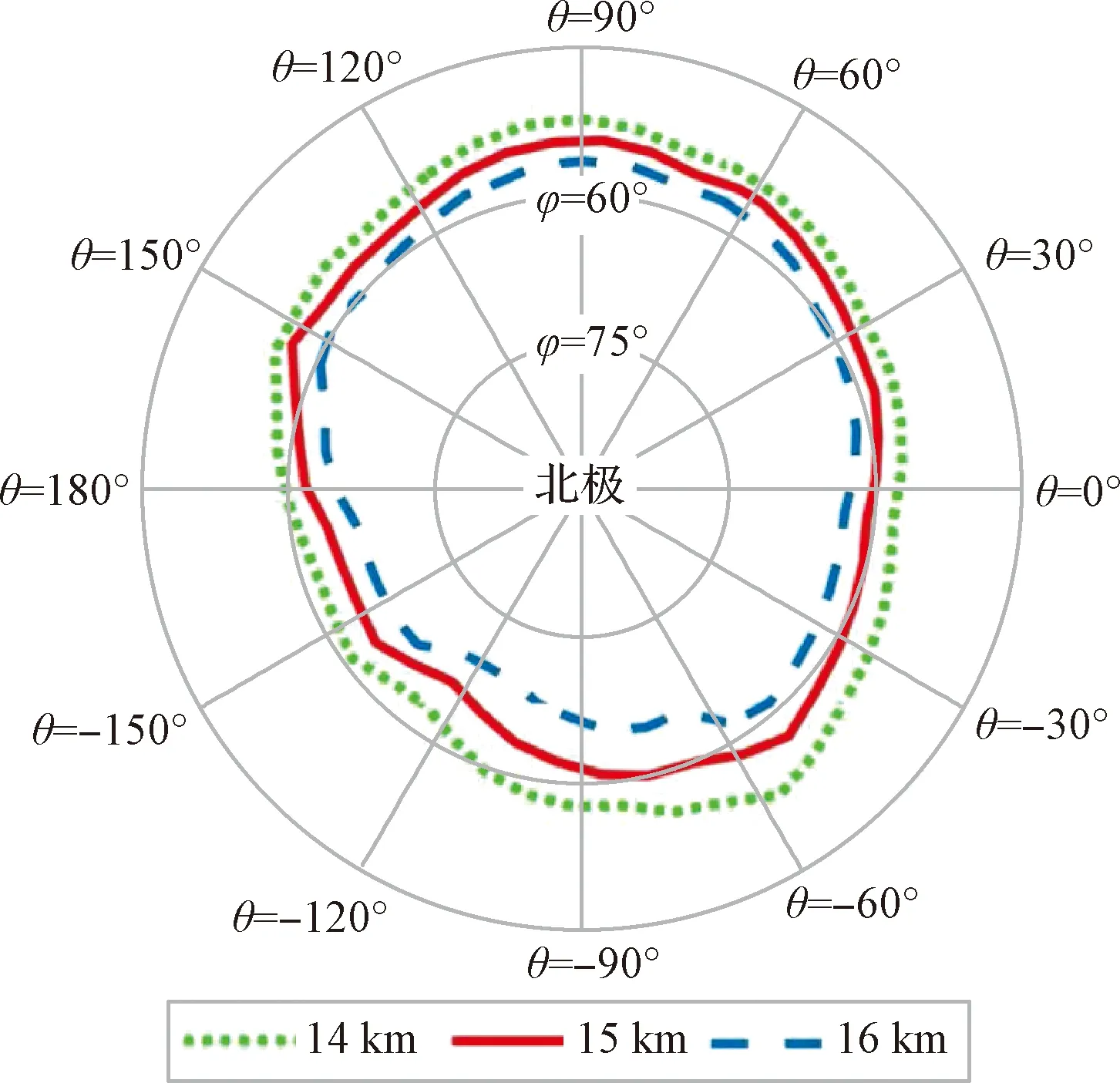
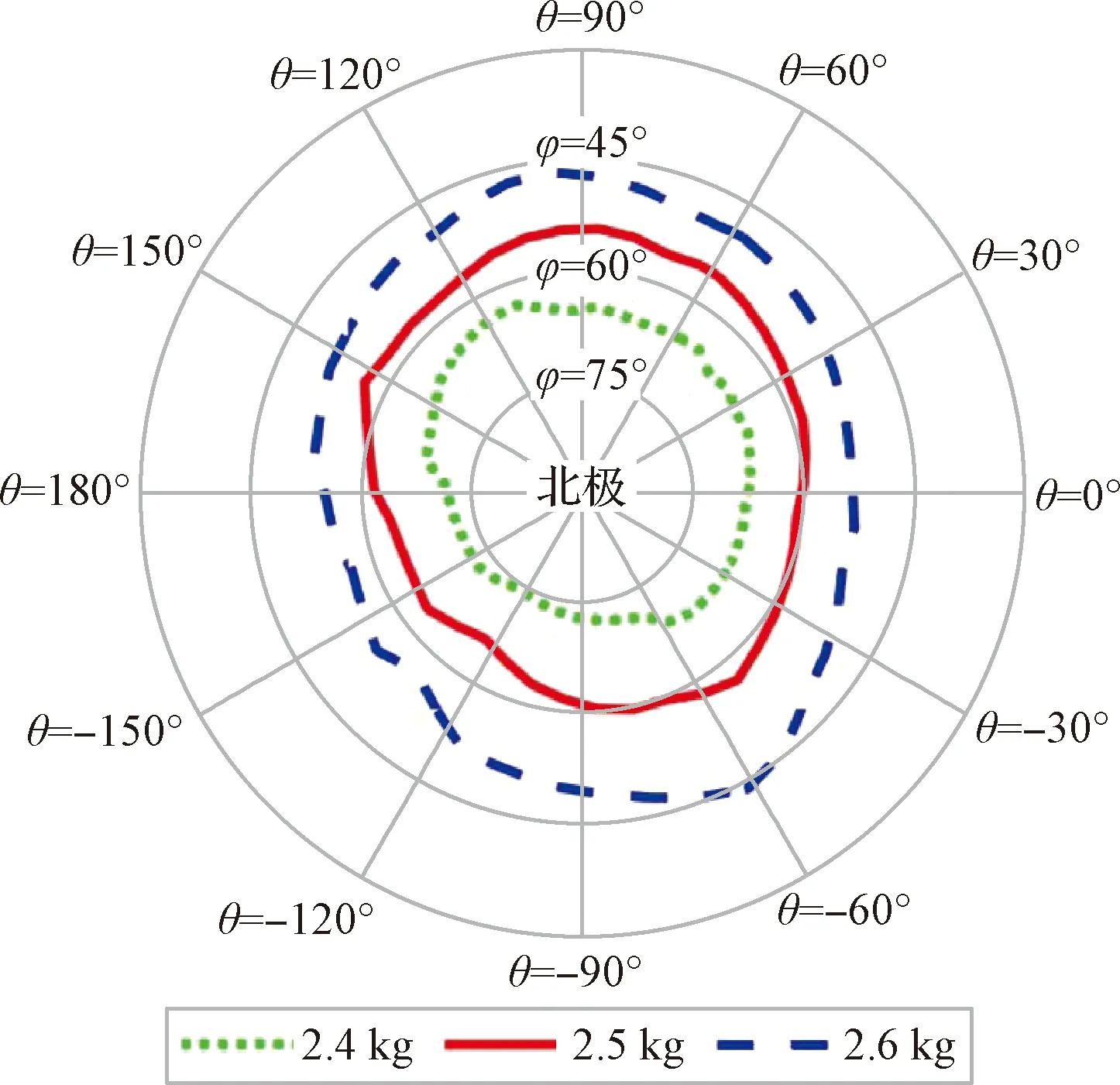
4 结 论

