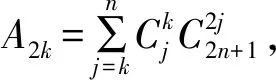由数学问题2268引发的再思考
李永利
(河南质量工程职业学院 467001)
1 引言
《数学通报》2015年10月号问题2268[1]:试证明
原解答利用正弦、余弦的积化和差等公式及一定的运算技巧给出了该恒等式的证明.文[2]、文[3]相继对该问题进行了探讨,从不同角度给出了该等式的精彩解答,文[2]提出了两个猜想,文[3]还提出了能否将该恒等式一般化的问题.近期,文[4]给出该式一个更为直接的证明,将其进行一般化,利用sin(4n-1)α和sin(4n+1)α所关联的方程证明了文[2]提出的两个猜想.受其启发,本文将对该问题进一步进行拓广,给出三角函数正弦的奇倍角公式所关联的一元奇次方程的解,作为推论利用韦达定理给出文[2]两个猜想的简单证明,并在文末提出一个有关组合系数A2k的猜想.
2 主要结果
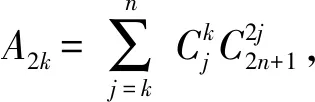

证明令x=sinα,y=cosα,则由平方关系可知y2=1-x2.于是对于正整数n,由棣模弗定理和二项式定理及i2=-1可知
cos(2n+1)α+isin(2n+1)α
比较上式两边的虚部可得
sin(2n+1)α



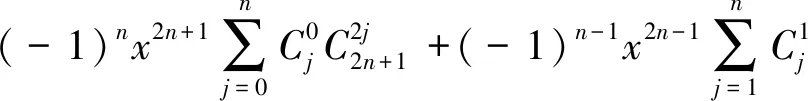
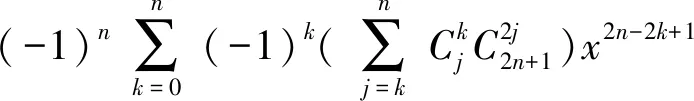
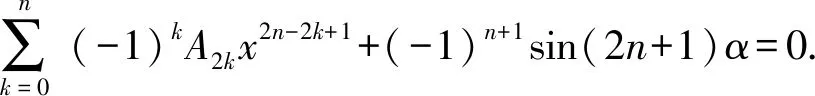
(2)
设(2)式左端为f(x),则f(x)是一个关于x的2n+1次多项式,其偶次幂的系数全部为0.
令sin(2n+1)α=0,则(2n+1)α=kπ,



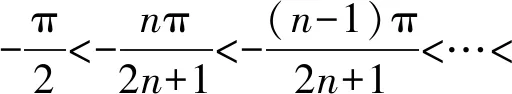
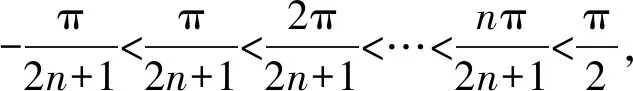

至此,定理1得证.

(k=0,1,2,3,…,n),则方程A0tn-A2tn-1+A4tn-2-…+(-1)n-1A2(n-1)t

证明在方程(1)中,令t=x2,则方程(1)变为方程(3),于是由定理1可知定理2的结论成立.
推论1设n为正整数,则
(4)
(5)

(6)
证明在定理2中,利用组合数的性质,经计算可知
于是,由定理2和韦达定理及以上三式可得
故(4),(5)两式成立, 从而(6)式也成立.
注1(4),(5)两式和(6)式分别是文[4]中的定理1和定理2,(6)式和(5)式分别是文[2]中的提出的猜想1和猜想2.
推论2设n为正整数,则
(7)
(8)
(9)
注2(7),(8),(9)三式见文[4]定理的证明过程,它们分别是(4),(5),(6)三式当n取2n-1时的特例.
推论3设n为正整数,则
(10)
(11)

(12)
注3(10),(11),(12)三式见文[4]定理的证明过程,它们分别是(4),(5),(6)三式当n取2n时的特款.
推论4设n为正整数,则
(13)
(14)
(15)
注4因sin2α=1-cos2α,故(13)式是(4)式的变形,(14)、(15)两式分别是(13)式当n取2n-1和n取2n时的特殊情形.
推论5设n为正整数,则
(16)

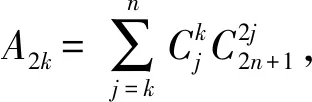

证明在方程(2)中,令sin(2n+1)α=1,此时方程(2)变为方程(17),则
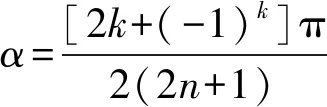

取k=0,±1,±2,…,±n,并记

α-n<α-(n-1)<…<α-1<α0<α1<…<αn-1<αn,

x-n 定理3得证. 在方程(2)中,令sin(2n+1)α=-1,此时方程(2)变为方程(18),仿照定理3的证明可给出定理4的证明,证明过程此处从略. 进一步,我们可将定理3和定理4进行拓广,得到如下更一般的结论: (其中,k=0,±1,±2,…,±n). 由定理5和韦达定理可得如下恒等式: 推论6设n为正整数,α为实数,则 (20) (21) 注6关于A2k的表达式,除A0=4n外,笔者提出如下猜想,供各位同仁研讨. 猜想设n为正整数,