为运算找出路 发展运算素养①——以2020年高考数学山东卷第22题为例

郭建华 于 健 宁连华 张云飞

(1．江苏省南京市金陵中学 210005； 2．南京师范大学数学科学学院 210023；3．南京市鼓楼区教师发展中心 210017)

1 问题提出

圆锥曲线是一个重要的数学模型，具有很多优美的几何性质，在日常生活、社会生产及科学技术中都有着重要而广泛的应用．运用代数方法解决几何问题是解析几何的核心思想，其中圆锥曲线综合题是每年高考的必考题型，它也是高中数学教学的难点之一．虽然学生在考前都做了大量的习题，但是考生在考场上遇到圆锥曲线综合题时，还是束手无策、举步维艰．“会而不对，对而不全，全而不优”的现象普遍存在，究其原因是学生害怕其“运算”，具体表现为对运算对象的理解、运算法则的掌握、运算思路的探究、运算程序的设计和运算路径的选择上存在不足．因此，在平时的教学中教师要不断为学生创造自主探究的机会，调动学生的多种感官，在做中学、学中悟、悟中思，加强对运算能力的培养．教师在常态课堂教学中应多关注学生的运算过程，指导和帮助学生为“运算”找出路，通过运算教学促进学生思维的发展，从而形成规范化思考问题的品质，发展学生的数学运算素养．

日前，笔者所在学校高三的一次月考中，选用了2020年山东省数学高考第22题作为压轴题，学生的卷面反应与教师的预期差距较大，结果不甚理想．笔者借此机会进行了一些思考，并尝试在课堂上和学生一起探究，反馈效果较好．现将拙见整理成一些文字，望得到读者的指正.

2 真题再现

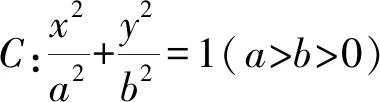
(1)求C的方程；

(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

本题以考查椭圆中的定点问题为载体，其背景熟悉、表达简练、内涵深刻．试题蕴含了等价转化、数形结合、函数与方程等数学思想．同时实现了对基础知识、基本技能和基本数学思想的考查，能较好地甄别学生的思维水平和检测学生的数学素养及学习潜能．

试题的命题特色如下：一是动静结合，化动为静；二是化繁为简，实现质的突破．这两点既是本题的亮点，也是难点．

3 解法探究

处理圆锥曲线问题一般要经历以下几个环节：首先要明晰解决的目标是什么样的几何问题；其次要寻找解决目标所需要的代数条件是什么，再把几何问题代数化(有时候这个代数化的过程不是很直观，需要把几何问题转化为另一个等价的几何问题后再进行代数化)；第三步是利用已知的题设条件，分析这些条件的关联，研究并解决转化之后的代数问题；最后要返回去研究几何问题[1]．

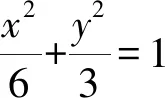
(2)这是一道与定点有关的问题，定点在哪儿，哪儿有定点?这是本题求解的关键点和难点．根据解题活动经验，定点一般存在于变化的直线或曲线中．注意到本题中的曲线为定的，而动的直线有四条，即：AM，AN，AD，MN，其中前三条都经过定点A，我们要找的定点不在这三条直线上，它最有可能在动直线MN上．利用教学软件GeoGebra演示，发现动直线MN的确过定点E，如图1．

图1

为了更利于学生理解直线MN过定点，设计其思维导图如下：

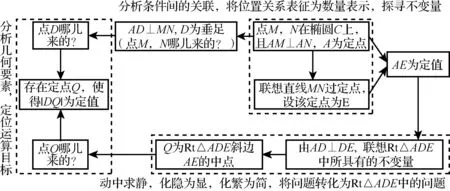
只有想得到，才能算得好．下面重点从运算的视角针对(2)中直线MN过定点问题做一些探究．

3.1 理解运算对象，为运算找出路

对于第(2)问，其中一部分同学的想法：先求出点M，N的坐标，写出直线MN的方程，再依据直线MN方程的结构特征探究它是否过定点．由于直线MN的斜率和它在y轴上的截距都是与k有关的变量，二者之间的关系比较隐蔽，学生未能理解运算对象间的内在关联，导致解题失败．其解法如下：

解法1：如图2，当直线AM的斜率存在时，设直线AM：y=k(x-2)+1，M(x1，y1)，N(x2，y2)，代入椭圆C的方程，消去y得

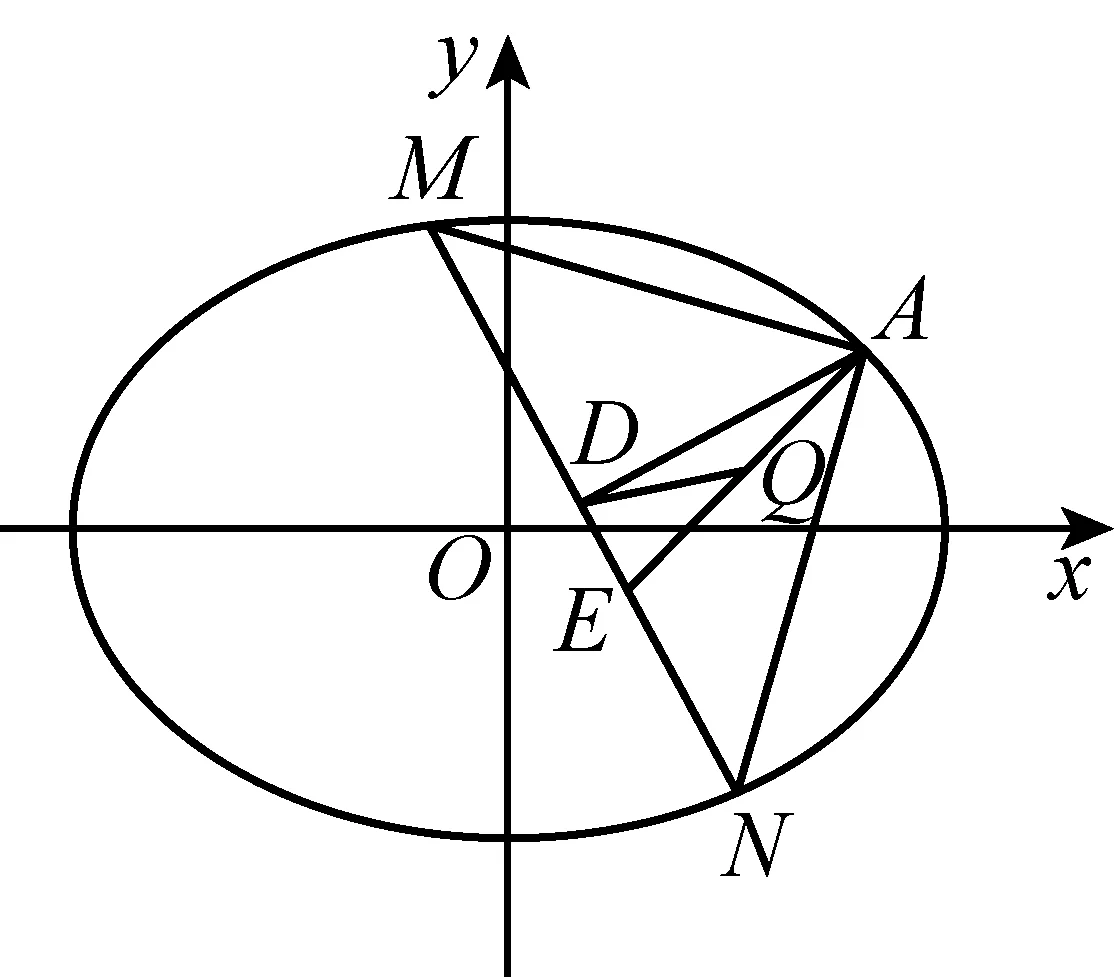
图2

(1+2k2)x2+(4k-8k2)x+8k2-8k-4=0①，

由题意得2为方程①的一个根，

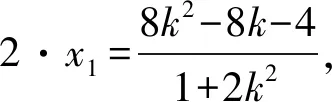
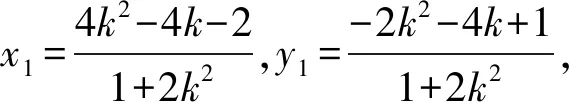
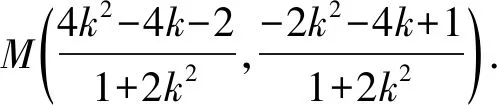
又AM⊥AN，

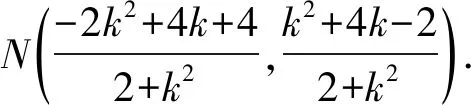
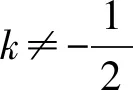
由直线MN：y-y1=kMN(x-x1)得

大部分同学写到这里就做不下去了．

教师可利用这个契机，让学生重新认识直线过定点的问题，并联想与定点相关的直线方程的形式：(1)点斜式：y-y0=k(x-x0)，直线过点(x0，y0)；(2)将直线方程转化成关于参数λ为主元的方程，即λ(A1x+B1y+C1)+A2x+B2y+C2=0，直线过两直线A1x+B1y+C1=0与A2x+B2y+C2=0的交点；(3)斜截式：y=kx+b．让学生思考：如果直线过定点，那么该定点与k，b存在怎样的关系?引导学生发现和提出问题，让学生动手操作，得出结论：(1)当b为定值时，直线过定点(0，b)；(2)当b=mk时，直线过定点(-m，0)；(3)当b=mk+n时，直线过定点(-m，n)，这种情况更具有一般性．于是上述学生的困难，便迎刃而解．其解法如下：

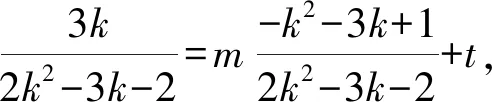
整理得(2t-m)k2-(3m+3t+3)k-2t+m=0，

于是得直线MN：

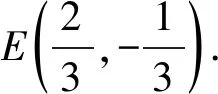
如图3，当直线MN的斜率不存在时，

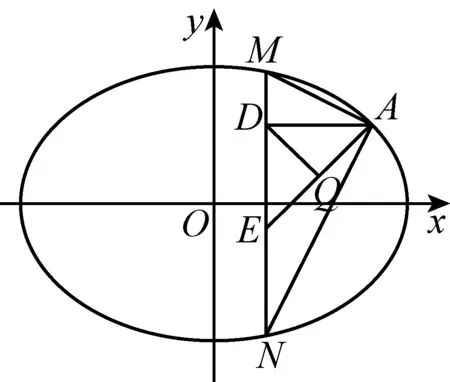
图3

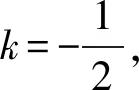
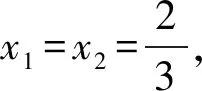
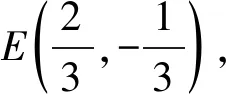
由于|AE|为定值，并且AE为直角△ADE的斜边，所以AE中点Q满足|DQ|为定值，即

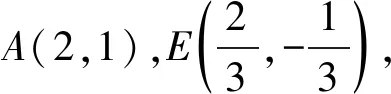
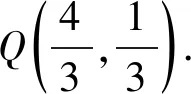
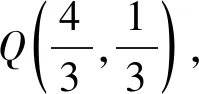
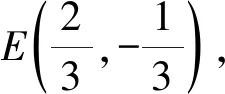
3.2 掌握运算方法，为运算找出路

也有同学这样想：既然目标是探究直线MN过定点，设直线MN：y=kx+m进行求解，但依然会被运算挡道．其解法如下.

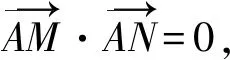
即(x1-2)(x2-2)+(y1-1)(y2-1)=0①，

当直线MN的斜率存在时，

设其方程为y=kx+m，并联立椭圆C的方程，

消去y得 (1+2k2)x2+4mkx+2m2-6=0，

由韦达定理得

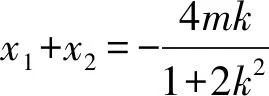
将y1=kx1+m，y2=kx2+m，代入①中得

(1+k2)x1x2+(mk-k-2)(x1+x2)

+(m-1)2+4=0④，

再将②、③代入④中，得

+(m-1)2+4=0，

上式可化为4k2+3m2+8mk-2m-1=0⑤.

一部分学生费了九牛二虎之力得到⑤式，后面就不知道如何计算了．

教师提出问题：观察运算对象所满足方程的结构特征，同学们能想到什么?停顿，让学生分析和思考．学生2提出了自己的想法：把⑤式看做以k为“主元”的一元二次方程，其判别式Δ=16(m+1)2>0(m≠-1，否则直线MN过点A)，

利用求根公式求得

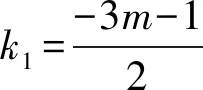
于是⑤式可化为

即(2k+3m+1)(2k+m-1)=0⑥，

由于点A不在直线MN上，所以2k+m-1≠0，

于是2k+3m+1=0，

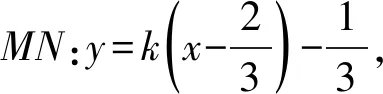
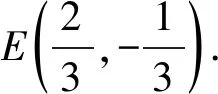
在学生2的启发下，学生3也提出自己的想法：其实，对⑤式的处理其本质是“降次”，而因式分解又是“降次”的工具，利用两次因式分解便可完成，即4k2+8mk+(m-1)(3m+1)=0，从而得⑥式．后面的解答同解法1．通过求根公式、因式分解等方法的选择，将运算目标分解并有机地融合到代数运算体系中，感悟因式分解在运算中的必要性，从而为运算找到出路．其目的是培养学生发现问题和解决问题能力，积累问题解决的基本活动经验，提高学生的认知水平．

3.3 借助平移变换，为运算找出路

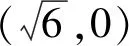
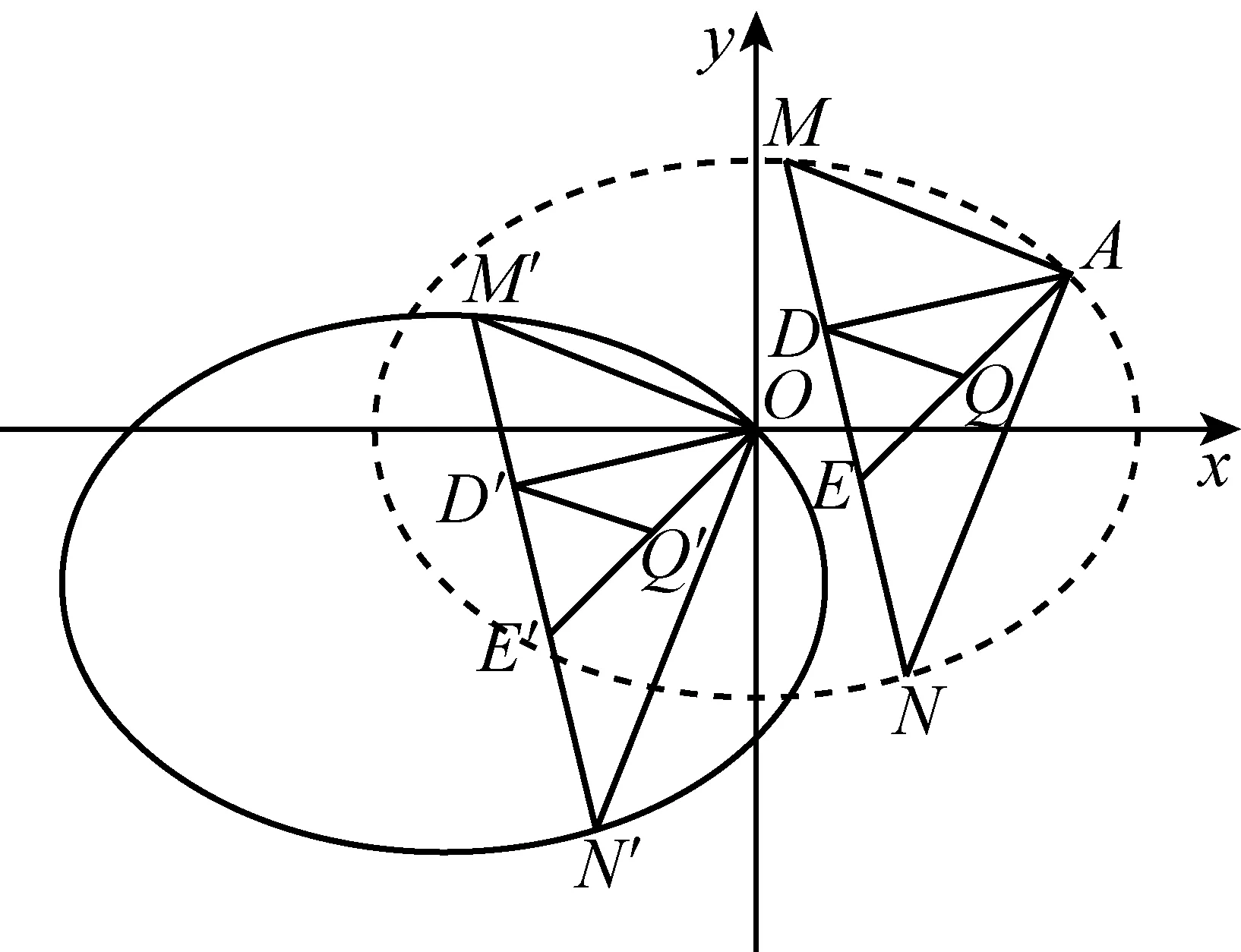
图4

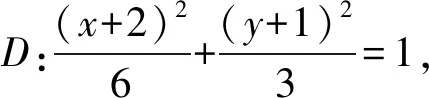
设M′(x3，y3)，N′(x4，y4)，由OM′⊥ON′，

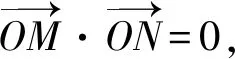
当直线M′N′斜率存在时，设直线M′N′：

y=kx+m(m≠0)，即点O不在直线M′N′上，

联立直线M′N′与椭圆D的方程，

消去y并整理得

(1+2k2)x2+(4mk+4k+4)x+2m2+4m=0，

由韦达定理，得

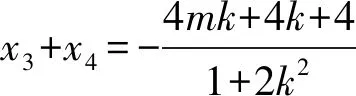
将y3=kx3+m，y4=kx4+m代入①中，

整理可得

(1+k2)x3x4+mk(x3+x4)+m2=0④，

上式可化简为m(3m-4k+4)=0⑤，

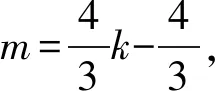
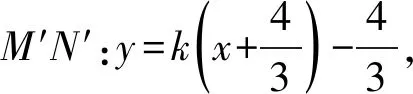
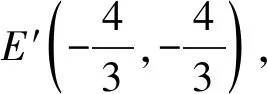
当直线M′N′的斜率不存在时，易证直线M′N′也过定点E′，

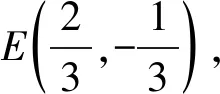
即直线MN过定点E，以下同解法1．

在平时的教学中要让学生关注和了解一下平移变换的实质，即：平移变换仅改变图形的位置，不改变它的形状和大小．利用平移变换得到的⑤式明显比解法2得到的⑤式简洁，并且将变量m与k的线性关系由“隐性”变为“显性”，降低了运算难度．平移变换为该题求解提供了一个工具，也为简化运算找到一个新的出路．

3.4 深度理解方程，为运算找出路

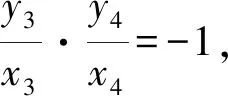
将①式变形为x2+2y2+4x+4y=0②，

当直线M′N′的斜率存在时，设直线M′N′：

将③代入②中，

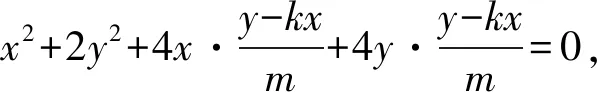
化简并整理为

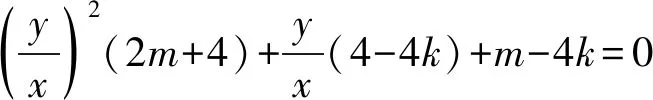
设直线OM′，ON′斜率分别为k1，k2，

由题意得k1，k2为方程④的两个相异实根，

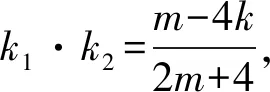
又OM′⊥ON′，得k1·k2=-1，

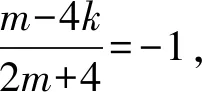
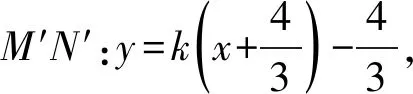
解法一出，同学们便自发地鼓掌，感叹其思维深刻、解法巧妙、运算简洁．紧接着让学生感悟、反思、梳理巧法背后所隐藏的思维路径．

在解法不断优化的过程中，让学生感受“数”与“形”的对立统一，渗透运动变化、相互联系、相互转化的辩证唯物主义观点，发展学生的数学运算素养，培养学生良好的思维品质．

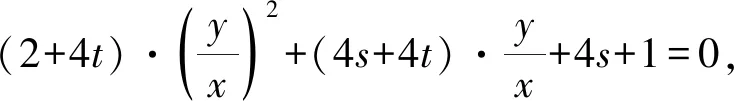
4 结论推广

学生9提出：如果本题中直线AM与AN的斜率之积为某一定值，那么直线MN是否过定点?能否得到一个更一般的结论?学生9将问题的探究又向前推进一步．经过笔者和学生一起探索，得到如下结论.

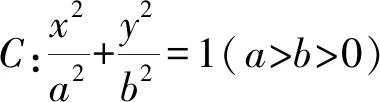
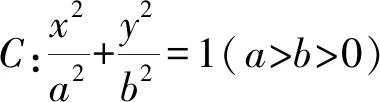
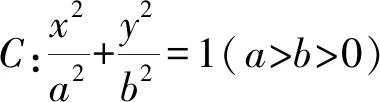
点M，N按向量n平移后分别对应点M′，N′，由椭圆D得

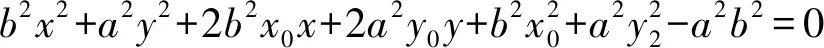
联立方程①、②得

b2x2+a2y2+2b2x0x+2a2y0y=0③，

当直线M′N′的斜率存在时，

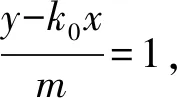
将其代入③式得

化简并整理为

a2(m+2y0)y2+(2b2x0-2a2y0k0)xy+b2(m-2k0x0)x2=0④，

将④式两边同时除以x2(x≠0)，得

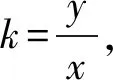
a2(m+2y0)k2+(2b2x0-2a2y0k0)k+b2(m-2k0x0)=0⑤，

由题意得k1，k2为方程⑤的两个相异实根，

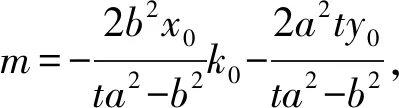
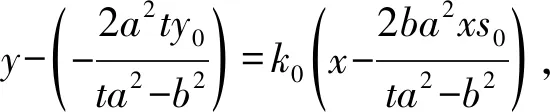
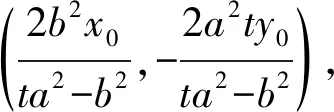
设平移前直线MN过定点E(x1，y1)，由题意，得

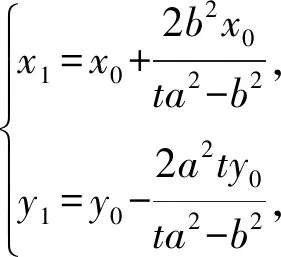
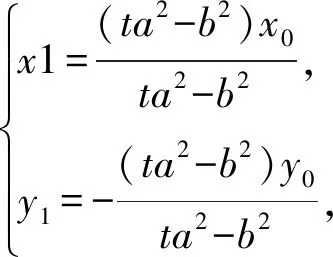
所以平移前直线MN过定点

当直线MN的斜率不存在时，易证点E也在直线MN上，综上，直线MN过定点

结论1的证法与结论2完全相同，本文不再赘述．

通过对一般性结论的探索，让学生体会平移法在解决圆锥曲线问题中的优越性，让学生感悟整体法在处理圆锥曲线运算中的妙用．学生在探索优化运算的过程中，应养成独立思考和勇于质疑的习惯，同时也应学会与他人交流合作，建立严谨的科学态度和不怕困难的顽强精神[2]．

教师继续抛出探究问题，在双曲线和抛物线中是否也存在类似的结论．供有兴趣的同学开展课外研究性学习．

5 结语

《普通高中数学课程标准(2017年版)》指出：数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养．它不仅是一种特殊的逻辑推理，而且能较好的甄别学生解决问题的能力．数学核心素养的四个方面“情境与问题、知识与技能、思维与表达、交流与反思”在这道高考题的探究中得到较好的体现和诠释，为促进学生数学思维发展，形成规范化思考问题的品质提供载体．由于解析几何是运用代数的方式解决几何问题，涉及到“数”与“式”的灵活转换和整合，“运算”便成了问题解决过程中的“拦路虎”．因此，在平时教学中要引导学生从多元视角分析影响运算的主要因素，加强对理解运算对象，掌握运算法则，探究运算思路等数学运算本质的理解和运用，不断渗透数学思想和方法，从而发展“四基”和提高“四能”．通过提升学生的运算素养，让学生养成用数学的眼光发现和提出问题，用数学的思维分析和解决问题，用数学的语言表达和交流问题的习惯，将数学运算素养的培养落到实处．