数学学科核心素养导向的“三角函数”教材内容变革①

张定强 梁会芳 杨 怡

(西北师范大学教育学院 730070)

1 研究背景

数学学科核心素养是落实立德树人根本任务的重要抓手，是数学课程目标的集中体现.而数学学科核心素养的落实离不开数学教材.新一轮的教材修订是在贯彻《普通高中数学课程标准(2017年版)》基本理念与要求的基础上，秉持继承创新的原则，通过对已有教材的分析思考、调研论证，重新建构了教材的编写思路与表征方式，力求充分地体现数学学科核心素养.三角函数作为一类典型的周期函数，在高中数学教学内容当中占据着重要地位.本文基于数学学科核心素养导向的视角，通过对比人教社2004年出版的《普通高中数学课程标准实验教科书数学必修4(A版)》[1](简称2004年版)与2019年出版的《普通高中教科书数学必修第一册(A版)》[2](简称2019年版)的“三角函数”内容的变革，以期为数学课程改革中新教材的使用提供一定的参考素材.

2 教材内容变革的对比分析

教材是学生获取知识的重要来源，也是教师开展有效教学的重要依据.数学教材的编写必须全面落实立德树人的基本要求，体现数学学科的育人价值，下面结合两版教材的结构表征与内容特征，从顺序安排、栏目设置、图表设置、例习题设置、知识要素、素养要素等几个方面对其进行对比分析[3]，解读两版教材在数学核心素养导向下的重要变革.

2.1 教材结构表征分析

2.1.1 编排顺序

对新旧两版教材三角函数内容进行比较分析，其分布情况如表1所示.

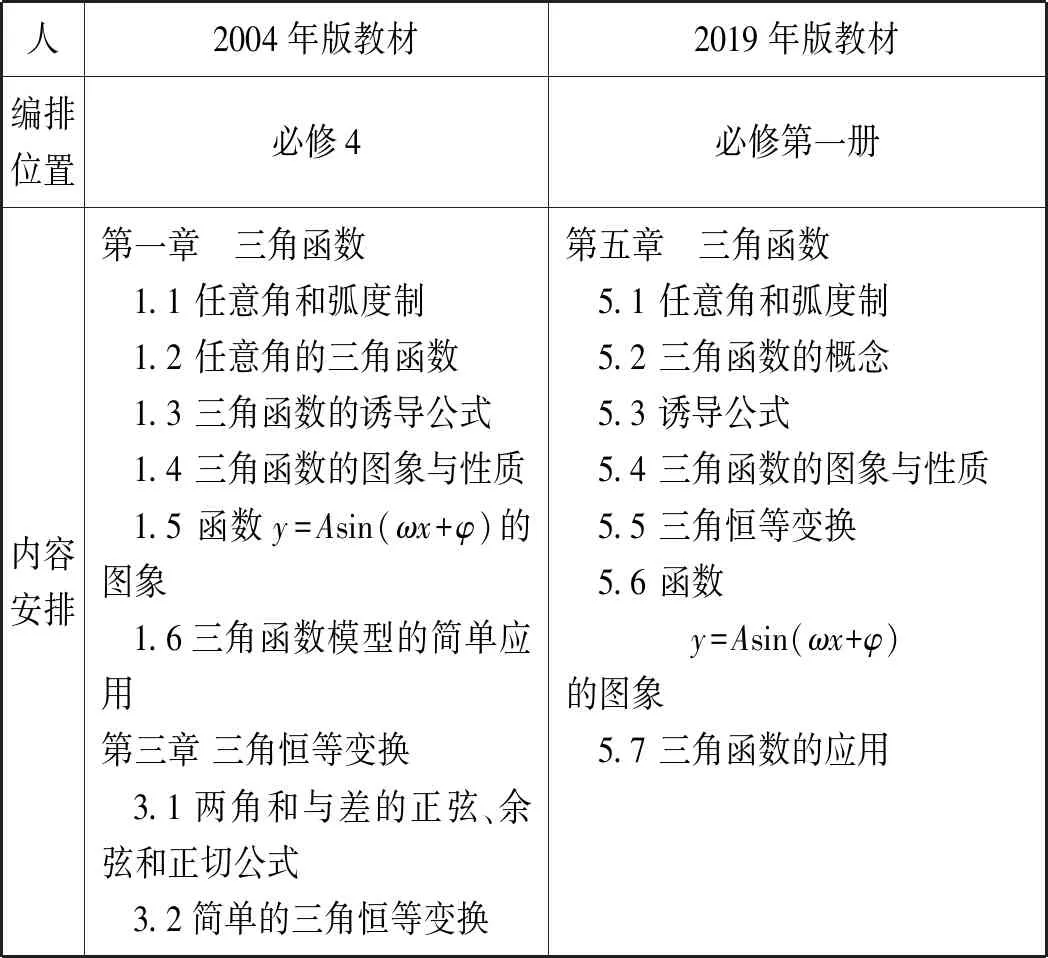
表1 新旧教材三角函数部分内容分布情况

2004年版将其安排在必修4，并分两章呈现，中间间隔一章；2019年版围绕函数主线对三角函数内容进行系统重构，将所涉及的内容调整到必修第一册的第五章，与函数的概念、性质、基本初等函数等构成一个整体，更加凸显了数学知识之间的逻辑连贯性以及思想方法的前后一致性，有助于教师进行“三角函数”主题单元教学设计.

2.1.2 栏目设置

教材中的栏目是表征知识的一种方式，也是体现教材建构特色的一种形式，蕴含着丰富的教育教学价值.对新旧两版教材栏目设置进行对比分析，结果如表2所示.

表2 新旧教材栏目设置

由表2可知，新旧两版教材的栏目设置类型丰富，使教材更具趣味性、拓展性与应用性.2019年版新增的“归纳”、“文献阅读与数学写作”、“数学建模”、“数学探究”等栏目，使数学文化、数学建模、数学探究等数学学科核心素养据此落到实处；统计发现，2019年版在三角函数这一内容新增10个“探究”栏目，是2004年版的近2倍，足见2019年版十分注重数学探究思想的渗透，以强化学生的探究意识和创新精神；就栏目的编排顺序而言，2019年版对旧版部分栏目的顺序进行了适当的调整，如“振幅、周期、频率、相位”这一阅读与思考栏目，在修订的过程中将其后移至“三角函数的应用”一节习题后，更符合学生的数学逻辑思维习惯；就栏目的内容结构来看，2019年版在吸收、继承旧版经验的基础上，适当性地穿插了一些开放性的问题，以引发学生思考，揭示知识所蕴含的数学思想方法，从而拓展学生的思维方式，发展学生的数学核心素养.

2.1.3 图表设置

图表作为表征数学知识的重要工具，可以使学生直观、形象地理解抽象的数学概念与性质.对新旧两版教材中图表的设置情况进行统计，结果如表3所示.其中解释图是指除函数图象之外教材中文字描述时作为例子相应出现的图以及例习题所对应图形[3].

表3 新旧教材三角函数部分图表设置

三角函数作为一类典型的周期函数，借助单位圆及其图象可以更直观地探究其概念、性质与应用，由表3可以看出，两版教材在编排的过程中其解释图与函数图占比较大.此外，两版教材图表的使用频率存在一定的差异，2004年版这部分内容分两章，共96页，其中课文插图、习题配图共81幅，平均图文比为0.84；而2019年版仅一章，共91页，其中课文插图、习题配图共90幅，平均图文比高达0.99，2019年版的图表使用频率高于旧版，更有助于学生直观想象素养的发展.

2.1.4 例习题设置

例习题是教材体系的重要组成部分，承担着巩固新知与训练思维的作用.现就新旧教材中的例习题从数量、类型两个方面进行对比分析.

(1)例习题的数量

对新旧两版教材三角函数部分例、习题数量进行统计分析，结果如图1所示.

图1 新旧教材三角函数部分习题数量统计情况

如图1表明，2019年版三角函数部分的例习题总量略低于2004年版，是在2004年版例习题的基础上重新审视与筛选，保留原有习题190道，删除部分重复、繁琐、过难、超标的题目68道，新增49道，有效地提高了例习题的针对性与有效性.具体而言，例题作为数学思维的示范引领，在2019年版中，保留原有例题33道，新增7道，删减7道，并依据实际背景及前后衔接，部分保留题目的数据及内容做了适当的调整；练习题承担着巩固知识、反馈教学的功能与作用，2019年版保留原有练习题63道，新增19道，删减13道，2处合并，并根据这部分内容的学业要求，部分题目的小题数量有所增减；习题承担着深化理解、拓展知识、学业评价的功能，在此次修订中，保留原有习题94道，新增23道，删减48道，18处合并，且习题的层次划分由原先的“A组”、“B组”变为“复习巩固”、“综合运用”、“拓广探索”三部分，由浅入深，使学生在巩固练习、综合应用的基础上，进一步感悟数学基本思想.总体而言，2019年版例习题系统的容量更加科学、准确，针对性更强.

(2)例习题的类型

教材中多样的例习题类型不仅可以促进学生巩固和掌握知识点，而且可以提高学生多方面的数学素养.对新旧两版教材三角函数部分习题的类型进行统计，结果如表4所示.

表4 新旧教材三角函数部分习题类型分布

总体上看，两版教材题型基本相同，都以传统题型为主.由于三角函数部分涉及公式较多，且变化灵活，对学生的运算素养要求较高，因此2019年版教材在建构中，延续旧版计算题居多的特点，通过反复的计算练习，以加深学生对公式的理解和记忆；此外，选择题的比例有所上升且简答题的比例下降，由于选择题是各类考试常见的题型，增加其比例有助于弥补以往学考不协调的弊端；探究题与作图题是培养学生应用意识与实践能力的主要载体，基本保持原有的建构体例，事实上还可适当增加题类的开放度与占比，以提升学生的数学建模和直观想象等素养.

2.2 教材内容特征分析

2.2.1 知识要素分析

(1)知识比重

所谓知识的比重，是指各知识点占教材编排体系的比重.由表1可知，新旧教材除了编排体系有所不同之外，所包含的知识内容基本一致.对新旧教材三角函数部分各知识所占比重进行统计分析，结果如表5所示.

表5 新旧教材三角函数部分各知识所占比重

由表5可得，在“三角函数概念”部分，通过对“三角函数线”这一知识点的删减，知识比重虽有所下降，但2019年版在修订的过程中，以简驭繁，通过利用单位圆上点的运动规律引入概念，更有利于学生把握知识的本质.此外，三角函数作为一类特殊的函数模型，2019年版中“图象与性质”所占知识比重在2004年版的基础上，上升了4.1个百分点，占比高达37.9%，强化了这部分内容的学习.另外，三角函数部分总共包含22个公式，且变化灵活，对于学生的运算素养要求较高，2019年版注重借助单位圆的性质直观明了地导出公式，更有助于学生的理解与掌握.而三角函数的模型应用是学生体会三角函数的价值与作用、增强应用意识的重要载体，但新旧两版教材“三角函数的应用”占比相对都比较小，有待提高.

(2)学科知识联系

随着跨学科知识融合的STEM教育的不断推进，学科知识的整合取向成为学生学习创新的载体.教材通过寻找不同学科知识之间的联结点与整合点，使各学科知识逻辑结构化，更有利于学生对数学知识建立完整的认知.通过对新旧教材三角函数部分所融入的各学科知识进行统计，其结果如表6所示.

表6 新旧教材学科知识联系对比分析

表6显示，新旧两版教材三角函数部分学科知识的融入从类型上来说基本一致，都涉及了物理、信息技术、地理、天文、历史等多个学科.其中，物理与信息技术方面融入最多，地理、天文方面次之，物理当中的匀速圆周运动、简谐运动以及交变电流都是研究三角函数的理想模型.但从融合方式及融合深度上来说，两版教材存在一定的差异.如在信息技术的应用方面，2004年版与信息技术的融合停留在表层，应用形式单一，大多是利用计算器进行繁琐计算，未能真正有效发挥信息技术的价值和作用.而2019年版充分落实课程标准提出的信息技术与课程深度融合的理念，注重信息技术应用的多样化，如利用信息技术工具进行角度制与弧度制的单位互换、探究三角函数图象以及借助信息技术进行数学实验等，将信息技术由计算工具演变成数学问题的研究工具与认知工具，以此形象化地说明周期变化现象，增强了教材的直观性.

2.2.2 素养要素分析

发展学生数学学科核心素养是数学课程的核心目标，同时也是教材编写的根本宗旨[4].数学教材内容素材的选取与编排、学习活动的设计与创新以及习题系统的构建与形成都必须以培养和提高学生的数学核心素养为目标.

(1)概念引入中的素养

三角函数作为一类最典型的周期函数，在章节起始，教材就通过学生所熟悉的周而复始的自然现象引入研究对象，使其研究问题显性化，有助于促进学生数学抽象素养的发展.此外，概念的建构过程实则是一个数学化的过程，三角函数作为一种特殊的函数，是学生在学习完函数的相关概念之后的“下位学习”，2019年版编写者充分利用学生已有认知基础当中圆的性质、相似形的知识以及研究函数的经验等，从建立周期现象的数学模型出发，借助单位圆上点的坐标定义三角函数，使学生从以“代数运算”为对应关系过渡到以“几何元素”为媒介的函数定义方式，以此破除学生已有思维体系当中研究函数模型的思维定势[5]，不仅有助于学生体会数学内在逻辑结构的整体性以及研究问题方法的多样性，同时借助单位圆直观特点，有助于发展学生的直观想象素养.

(2)知识建构中的素养

2019年版“三角函数”内容的编排，充分依据数学知识发生过程的内在逻辑结构，遵循章建跃教授所提出的研究一个数学对象的基本套路：背景—概念—性质—特殊性质—应用，通过对具有内在关联性的内容加以分析与重组，构建了一个研究三角函数模型的具体路径：从周而复始的运动现象出发，通过任意角与弧度制等预备知识的学习，利用单位圆上点的圆周运动给出三角函数的概念，进而通过图象探究其性质，并加以应用.通过这种严密的逻辑建构，使学生建立整体理解数学知识的意识，在研究问题的过程中实现知识与素养的融合.教师在教学过程中，要注重教材和教学主题思想的一致性，在整体研究思路的指导下，将知识局部系统化，加强主题单元教学的设计，完善学生的认知结构，从而提升学生的逻辑推理素养.

(3)思想方法中的素养

数学思想方法是发展学生数学核心素养的有效载体.2019年版十分注重数学思想方法的显性化，如通过“探究”、“思考”、“归纳”等栏目的设置，使学生在解决问题的过程中掌握类比、归纳、推理等数学思想；通过借助单位圆的直观特点及性质对三角函数的整章进行研究，使数形结合的思想贯穿始终.此外，教材从章引言提供的情景出发，使学生从学习之初就建立起从数学模型的角度审视三角函数的意识，并通过学科背景之间的联系，使学生螺旋上升抽象出三角函数模型，在反复理解与应用的过程中，发展学生的数学抽象与数学建模素养.

3 结语

数学教材为数学教学提供学习主题、基本线索和具体内容，也是承载数学思想、发展学生数学核心素养的教学资源.基于以上新旧两版教材三角函数内容的对比分析，发现2019年版不断地凸显数学学科核心素养，无论是教材的结构表征，还是内容特征都着力于数学核心素养的渗透.因此教师在解读和运用教材时，要在注重数学思想方法渗透的基础上着力于提升学生的数学学科核心素养；在注重知识系统化理解的基础上强化单元教学设计；在强化信息技术应用的基础上重视学科间的纵横联系.