借助几何直观 强化逻辑思维

林彩霞

摘要：随着教育行业的不断发展，数学作为理科科目的基石需要进行相应的改革，改革应适应学生的接受能力需求，提高学生们对数学的掌握能力.几何直观作为数学教学中的重点内容要求教师在教授学生数学的过程中，不断强调“数形结合的思想”，将几何图形的直观性和数学本身的抽象性融合在一起，帮助学生更好的掌握数学知识.本文就从几何直观的内涵和优势方面出发，系统地分析几何直观在初中数学教学上的运用，给教授数学的初中教师提供一些参考经验.

关键词：几何直观;逻辑思维;初中数学教学应用

引言：

几何直观凭借图形进行数学知识的探索和理解，由于低年级学生本身的思维阶段特质决定了年幼时他们的“化抽像为具体”的思维习惯导致了他们在学习数学时偏向将抽象的数字借助几个图形以及空间立体想象能力来处理抽像的数学，在这个过程中，他们能更好的理解初中数学教师讲解的初中数学中的数的关系，更高效的抓住数学知识的本质，提升学生的解题速度和答案的正确性.

一、几何直观的内涵和优势

几何直观的运用能够让初中生更轻松的接触数学知识，借助几何直观来强化自身的逻辑思维.将抽象形式具化为几何图形，既符合了初中生的自身所处学习阶段的知识阶段和思维运转模式，也有利于教师在授课时能够通过更简单的几何直观向学生阐述抽象数学背后的逻辑思维.

几何直观的优势在于它的直观性，它不同于数学概念、数值等其他数学知识知识的抽象性，它能够让人们一目了然的获取信息.当然，除此以外，它最大的优点是连接抽象和具体的桥梁，它能够化抽象为具体，也能从具体中寻找到抽象.例如，一个一元二次函数，初中生既可以通过作图的方式来分析其特性也能通过数字计算的方式获取它的信息，这二者之间的表述内容相同，其表述效果不同罢了，相较而言，几个直观更简单，对初中生更为友好.

二、初中数学几何直观教学的应用

（一）几何直观在初中数学知识概念中的应用

几何直观能够帮助初中生更好理解数学中的定义.从某种程度上来说，初中的数学知识最简单也是最复杂也是最重要的部分在于数学的基本定义.作为数学专有名词中的定义，它往往简短，但它的复杂也是由此而来，它往往具有抽象性.在不借助图形的前提下，初中生们在理解数学的某些概念时就会感觉困难.例如，初中数学中的负数的概念，学生单纯依靠教师的文字讲解很难理解负数的概念.但是，当教师通过画出数轴的方式将负数标在数轴上.例如，“-2”作为负数应该出现在“0”的左边，“-5”应该出现在“-2”的左边，通过数轴图像同时能够更直观的对比二者的大小.几何直观在初中数学的概念中的应用使得初中数学的概念变得简单化，教师在教授该知识定义时结合图像能够让学生恍然大悟且更深刻的了解数学知识的概念，学生也能够通过几何直观轻松愉悦的掌握知识，提升初中生学习数学热情，激发初中生学习初中数學的兴趣，让学生从被动接受到积极主动的进行初中数学知识的探索.

（二）几何直观在一元二次函数教学过程中的应用

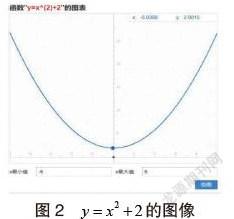
几何直观在初中数学中最有效最实用的应用是在初中数学的一元二次函数部分.通过图像，学生能够短时间内正确的寻找到一元二次函数的开口方向、对称轴、最值、性质.故而，几何直观在初中数学中最成功的案例就是一元二次函数的“数形结合”，它使得学生对一元二次函数本身一目了然，通过图像能直接获取几乎所有一元二次函数的相关的知识.

例如，的图像的开口方向向上，对称轴为y轴，顶点（0，2），它有最小值为2.这些都是几何图形在一元二次函数的运用中学生能够通过实际的作图获取的有效信息，如图2所示.

（三）几何直观在中考解题中的应用

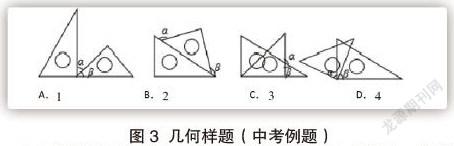
几何直观在初中数学上的几何教学中应用十分广泛.点、线、面的关系本身就涉及到几何图形以及空间的想象问题，作为中考的几何证明大题之一，它要求学生熟练运用点线面的关系的证明，证明角与角、线与线之间、图形与图形之间的关系.这要求学生在进行解题前利用直观的几何图像在大脑中直观化，利用基本的初中数学知识进行辅助线的作取，通过辅助线将原本表面上没有联系的线面进行联系.而这也是中考必考的难点重点内容，以下图3为例：

如图，一副三角尺按不同的位置摆放，摆放位置中∠a=∠β的图形的个数是（  ）

在上图的几何样题中，该数学题目是以两个不同的三角尺的摆放位置来构成不同的角度，它要求初中生通过几何直观的思维模式分析并探索该题目中隐含的数学逻辑.在图3中，它所隐含的数学逻辑有：三角形的三个角的内角和为180°、直线可以看作180°的角.而现实中的三角尺的形式基本分为图上的两种，一种是有45°、45°、90°的等腰三角尺，三个角度构成完整的180°.另外一把它的三个角度分别为：30°、60°、90°，同样这三个角的角度度数总和也是180°.在上图的几何样题的题目中，该题目明确指出让初中生寻找符合∠β=∠α的图形并确定它们的个数.通过常见的两种三角尺构造出不同的形状，创造出各种各样的角.在第一幅小图上，结合上述的隐藏条件可以得知∠β=45°，∠α=45°，满足题目的需求;在第二幅小图上，结合上述的隐藏条件可以得知∠β=135°，∠α=135°，满足题目的需求;在第三幅小图上，结合上述的隐藏条件可以得知∠β=60°，∠α=120°，不满足题目的需求;在第四幅小图上，结合上述的隐藏条件可以得知∠β和∠α无法确定，不满足题目的需求.综上所述，这条题目的答案就是2个.

三、结束语：

随着时代的发展，教育教学思想的层出不穷，初中生的数学教育也受到了影响.作为数学教育中最实用的教学手段，几何直观应当被初中数学教师作为一种教育思想运用到初中生的数学教学过程中，它能够帮助学生更好的理解抽象的数学概念和数学知识.它在初中数学教学应用中，大大降低初中的数学教师在讲解抽象知识的复杂程度和学生在接受这些这些抽象的数学知识，使得初中数学教师能够在课堂上跟学生进行更多的思想交流.

参考文献：

[1]姚蒋诗. 几何直观在初中代数教学中的有效落实策略研究[D].鞍山师范学院，2019.

[2]康琴琴. 利用GeoGebra发展初中生几何直观能力的行动研究[D].西北师范大学，2019.

[3]李江专. 基于几何直观的初中代数教学设计研究[D].重庆师范大学，2016.

[4]宋晓燕. 初中代数教学中培养学生几何直观的实践研究[D].重庆师范大学，2013.